冲击作用下钢筋混凝土框架抗连续倒塌数值模拟
2017-01-10何庆锋刘义仁易伟建
何庆锋, 刘义仁, 周 超, 易伟建
(湖南大学 土木工程学院,长沙 410082)
冲击作用下钢筋混凝土框架抗连续倒塌数值模拟
何庆锋, 刘义仁, 周 超, 易伟建
(湖南大学 土木工程学院,长沙 410082)
为研究冲击作用下钢筋混凝土框架结构的抗连续倒塌性能,采用有限元软件LS-DYNA对两个单层、四个三层钢筋混凝土框架在冲击荷载作用下的抗倒塌性能进行了数值模拟分析,计算过程中主要改变了框架梁的纵筋配筋率,对比分析计算了冲击作用下各框架的内力、位移以及破坏过程等。分析结果表明:冲击作用下,各框架梁均经历了明显的拱效应与悬索效应受力阶段,且配筋率越低,拱效应越明显;框架抗倒塌能力与框架梁配筋率有关,配筋率高的楼层承载能力较强,耗能能力较大,框架空腹作用能提高多层框架结构承载能力。基于数值计算结果,分析了框架结构在冲击作用下的抗倒塌能力以及加强措施。
连续倒塌;抗倒塌设计;冲击作用;LS-DYNA数值模拟
近年来对偶然荷载引起建筑毁坏(如恐怖袭击)的防护需求,使建筑结构的抗连续倒塌成为研究热点。从三次典型的连续倒塌事故可知[1-3],偶然荷载作用下结构发生连续倒塌存在两种模式,①由于底层结构局部关键支撑构件失效,导致上部结构发生连续倒塌;②中间楼层局部支撑构件失效引起倒塌后,上部结构对下部楼层产生冲击作用继而导致整体结构发生连续倒塌。不少研究者针对①倒塌模式进行了大量的研究,包括结构抗倒塌设计与抗倒塌机理等方面[4-9]。对于②倒塌模式的研究相对较少,随着高层以及超高层建筑的广泛运用,对②倒塌模式的研究显得尤为重要。
由于上部楼层连续倒塌而失效结构体的冲击速度来源于重力,而楼层高度一般在3~5 m左右,因此其冲击速度比较低,属于低速冲击范畴。有不少研究者基于落锤试验机试验装置对钢筋混凝土梁进行了低速冲击试验,基于试验数据,通过建立冲击承载能力与静力承载能力之间的关系[10-12],得到基于结构静力性能的冲击承载能力计算公式,但获取其冲击作用下钢筋混凝土梁的动力响应与破坏过程受力机理试验数据不易。随着计算机技术的发展,采用数值方法进行冲击荷载作用下模拟计算是研究者采用的主要研究手段,研究集中在采用有限元软件LS-DYNA和AUTODYN等对钢筋混凝土梁的冲击响应进行分析和计算,采用有限元软件能够直观的反映计算结构的受力特性和破坏状态,正逐渐成为冲击荷载作用下结构分析和辅助设计的手段。
为了研究冲击作用下钢筋混凝土框架的抗倒塌性能,本文采用有限元软件LS-DYNA,基于CSCM混凝土本构模型,对两个一层、四个三层等六个框架在0.5 m、1.0 m、1.5 m、2.0 m等四种冲击高度下的抗连续倒塌能力进行了分析,每榀框架梁柱截面尺寸均相同,主要变化了配筋率,即改变了其静力承载能力。基于分析计算结果,对冲击作用下框架的抗倒塌性能进行了讨论,并提出了相关设计建议。
1 冲击试验概况
为了验证用于冲击作用模拟的LS-DYNA软件相关计算参数,针对钢筋混凝土梁冲击试验进行了数值模拟计算。文献[13]共进行了四根钢筋混凝土梁的冲击试验,试验梁配筋以及尺寸见图1,冲击高度与冲击质量见表1。试验过程中主要测得了冲击力、支座反力、跨中竖向位移等冲击响应,并采用高速摄像机拍摄了试验梁的破坏过程,试验装置见图2。

图1 试验梁配筋以及尺寸Fig.1 Details of model frame

表1 试验梁冲击高度与冲击质量

图2 试验测试装置
2 试验数值模拟
2.1 有限元模型
采用1/4模型对试验梁进行数值建模。试验梁及锤头均采用实际尺寸,为了简化计算,对支座进行了简化处理,试验梁以及锤头有限元模型见图3。梁身混凝土、锤头以及支座采用实体单元,实体单元尺寸在12.5 mm左右,钢筋采用梁单元。混凝土采用CSCM本构模型,钢筋、支座以及锤头均采用*MAT_PLASTIC_KINEMATIC 本构模型。钢筋以及混凝土的材料特性均采用实测值。
采用关键字*CONTACT_ERODING_SINGLE_SURFACE_ID定义锤头与梁之间的冲击作用,采用关键字*LOAD_BODY_Y定义重力加速度,采用关键字*INITIAL_VELOCITY定义锤头的初速度,采用关键字*HOURGLASS控制沙漏。通过关键字*CONTROL_ENERGY、*CONTROL_TERMINATION和*CONTROL_TIMESTEP控制计算中能量、总时间和时间步长。由于计算采用1/4模型,在对称面上施加了对称边界条件(图3中的模型为对称复制后的1/2模型)。

图3 梁有限元模型
2.2 计算结果

图4 破坏状态比较
图4给出了试验梁计算损伤云图与实测裂缝图的比较(为方便比较,图中的模型均由1/4模型对称复制得到),其中删除的单元表示其最大主应变超过了0.3(=1.3-1),进行比较时主要对比损伤云图,而不是根据单元删除而产生的裂缝,因为一个单元的大小要比裂缝宽度大很多。损伤云图中红色表示损伤最严重,蓝色表示没有损伤。由图4可知,有限元模拟的损伤状态与试验结果吻合较好,梁的主要损伤区域为冲击荷载作用附近的梯形区域,又称为跨中区域,该区域的损伤程度、其他区域的斜裂缝与实测结果均吻合较好。支座处出现的局部损伤与试验略存在差别。
由图5可知,冲击力、支座反力和跨中位移时程曲线的计算结果与实测结果,冲击力计算值与实验值吻合较好,峰值处实验值略大于计算值,这主要与采集引入噪声数据有关。支座反力动力反应与实测结果存在差别,这主要是由于支座边界模拟与试验时存在较大差别,冲击过程结束后,支座反力的振动周期相对实测值偏小,这主要是由于计算模型中单元的删除,实测梁中出现混凝土的飞溅、破坏等导致计算模型与实际模型刚度存在一定的差别。除A4梁计算位移幅值略小于实测值外,其余梁的跨中位移时程曲线计算值与实测均吻合较好。数值计算表明,该文采用的用于模拟冲击作用过程的LS-DYNA数值计算参数能够较好反应钢筋混凝土梁在冲击作用下的受力过程与破坏形态。

图5 计算动力响应时程曲线比较
3 连续倒塌分析
3.1 有限元模型
基于前述的材料本构、单元类型、分析控制方法以及锤头形状,本文共对比计算分析了6榀钢筋混凝土框架(见表2),1-A框架配筋以及截面尺寸见图6,1-B框架仅改变梁纵筋,4个三层框架的每层梁截面尺寸以及箍筋均与1-A框架相同,每层柱的截面尺寸以及配筋均与1-A框架相同,仅改变了各层梁的纵筋配筋率。每榀框架分别计算0.5 m、1.0 m、1.5 m、2.0 m等四种冲击高度下的抗连续倒塌能力,采用全比例尺寸建模,柱底简化为固支约束。

图6 1-A框架配筋以及截面尺寸Fig.6 Details of frame(1-A)

表2 模拟计算框架信息汇总表
钢筋以及混凝土材料参数见表3,混凝土单元的删除应变取0.3(LS-DYNA中输入参数为1.3,删除应变为1.3-1=0.3),材料密度取2 300 kg/m3,混凝土达到抗压强度时,丧失承载能力。钢筋的弹性模量、屈服强度、极限强度根据采用相关试验结果[14], 根据相关文献[15]可知,钢筋屈服后伸长率达到10%则可认为其发生断裂,因此取钢筋屈服后塑性应变达到0.1作为其断裂的标准。

表3 计算模型材料参数
3.2 单层框架分析结果
3.2.1 倒塌过程分析
图7为1-A框架冲击荷载作用下的倒塌过程数值模拟计算结果,其计算冲击高度为0.5 m、冲击质量为388 kg。由图可知,冲击瞬时(4 ms),框架梁负弯矩处混凝土没有损伤,损伤主要集中在中柱附近。7 ms时框架梁负弯矩处混凝土开始出现损伤,这是冲击荷载作用下应力波在梁中作用的结果,且由冲击作用区域向两侧快速传递。7 ms时框架梁负弯矩处的混凝土损伤由下至上发展,这表明结构开始在发生变形。58 ms时,左侧负弯矩钢筋断裂,部分混凝土单元丧失承载能力,结构进入悬索效应受力阶段,左侧混凝土单元应变显著增加,此时中柱的竖向位移为97.65 mm(见图8),而静载作用下结构进入悬索效应阶段时竖向位移为216 mm,表明冲击荷载作用下结构进入悬索效应阶段之前由结构变形所吸收的能量相对静力荷载作用下偏低。96 ms时右侧负弯矩钢筋断裂,右侧混凝土单元应变显著增加,此时,结构仍具有一定承载能力。172 ms时中柱梁端受拉钢筋断裂,结构承载能力显著降低,变形迅速增加,结构发生倒塌,从以上分析可知,框架梁在冲击荷载作用下的受力过程和静载作用下类似。

图7 1-A框架倒塌过程
3.2.2 结构动力反应
图8给出了各框架梁反力(左右两侧梁的截面剪力之和)、中柱竖向位移以及柱顶水平位移时程曲线。由图8可知,由于惯性力作用,各框架梁端反力在冲击开始瞬间向下,随后在冲击力作用下迅速增加到正向峰值,其后随着框架梁损伤的增加,反力逐渐衰减直至结构倒塌破坏;≈400 ms时,各框架的承载能力均较低。1-A框架梁的最大反力在20~25 kN左右,1-B框架梁的最大反力在38~41 kN左右,受冲击高度变化影响较小,与文献[16]中得到的结论一致。根据相关试验研究,可以采用框架梁的反力表示其抗冲击承载能力。
从图8所示的竖向位移时程曲线可知,钢筋完全断裂前,结构具有一定的承载能力,其位移响应曲线为缓慢增长的曲线。塑性铰区域受拉钢筋断裂之后,部分框架仍可以通过悬索效应抵抗冲击质量产生的荷载而没有最终倒塌,如在1.0 m、1.5 m、2.0 m冲击高度下,1-A框架最终没有倒塌,但是其竖向位移较大(>400 mm),可采用该位移作为其最大抗连续倒塌能力。

图8 单层框架结构响应时程曲线
从图8所示的柱顶水平位移时程曲线可知,其位移变化规律均是先向外运动然后向内,表明框架梁的受力过程经历了明显的拱效应和悬索效应阶段,与静力受力过程类似。1-A框架的水平位移均大约为7 mm,1-B框架的水平位移约为5 mm,这表明随着纵筋配筋率的降低,拱效应现象更加明显。同等冲击高度作用下,两框架水平位移交点出现的时刻较接近,0.5 m、1.0 m、1.5 m、2.0 m冲击高度作用下其出现时间分别约为300 ms、200 ms、150 ms、140 ms,表明随着冲击高度的增加以及框架梁纵筋配筋率的降低,结构倒塌速度加快。
3.2.3 抗倒塌能力分析
表4给出了各冲击高度下1-A、1-B两框架的抗连续倒塌能力,由表4可知随着冲击高度的增加,结构连续倒塌所需的冲击能量也增加,对其进行拟合可以得到如图9所示的关系曲线,由图9可知,结构发生连续倒塌所需要的能量与冲击高度近似呈指数关系,其主要原因是随着冲击高度的增加,使结构连续倒塌所需的冲击质量下降,而冲击质量越低,冲击过程中的能量损失越大。由图8可知,1-B框架梁反力比1-A框架大,表明提高框架梁抗弯配筋率能够其抗冲击能力。

表4 一层框架抗连续倒塌能力

图9 抗连续倒塌能力-冲击高度曲线
3.3 三层框架分析结果
3.3.1 倒塌过程分析
图10给出了3-A框架在冲击高度0.5 m,冲击质量906 kg的倒塌模拟过程,由图可知在冲击瞬时(4 ms),一层框架梁没有损伤,损伤主要集中在二层、三层中柱附近,8 ms时各层框架梁均出现不同程度的损伤,这主要是冲击荷载产生的应力波作用的结果,8 ms后一层框架梁负弯矩区域混凝土损伤由下至上发展,这主要是由于惯性力作用导致的。44~48 ms 时二层负筋相继断裂,此时中柱竖向位移达到78 mm,混凝土的损伤程度较低,没有单元应变达到删除应变,54~56 ms时三层负筋相继断裂,163 ms时刻,一层正筋断裂,此时二层、三层钢筋断裂部位有部分混凝土单元被删除,表明局部钢筋断裂后,该区域的混凝土应变显著增长,229~245 ms时刻三层正筋相继断裂,236~258 ms一层负筋相继断裂,284 ms时刻所有受拉钢筋均断裂,此时中柱竖向位移为210 mm,此后结构位移迅速增加,大量混凝土单元被删除,结构发生倒塌破坏。

图10 3-A框架倒塌过程
3.3.2 结构动力响应
图11为各框架梁反力(各层梁截面剪力之和)、中柱竖向位移以及各层柱顶水平位移时程曲线。由图可知,3-A框架的最大反力约为64 kN,其余三个框架的最大反力约为80~88 kN,提高幅度约为16~24 kN,但单层框架1-B相对于1-A只提高约14~18 kN,表明冲击荷载作用下,由于框架结构的空腹作用,三层框架的承载能力提高幅度相对于单层框架结构略有提高,且随着框架梁配筋率的增大其承载能力也在提高。3-B、3-C、3-D三个框架的承载能力接近,表明提高任何一层框架梁的配筋率,均可同样提高整体框架承载能力。框架梁由于遭受多次冲击,其内力会出现多处负值,3-A框架遭受第二次冲击的时间滞后于其余三个框架,主要原因是同等冲击高度下,3-A框架倒塌所需的冲击质量较低,为其余三榀框架的0.57倍~0.64倍,导致其回弹高度相对较大,第二次冲击与第一次冲击时间间隔相对较大。
从图11所示竖向位移时程曲线可知,钢筋断裂前,3-A框架的竖向位移相对较小,表明增大各层框架梁配筋率能显著提高框架的变形能力,受拉钢筋完全断裂后,各框架的竖向位移迅速增加,3-B框架竖向位移增加速度相对较慢,表明提高底层框架梁配筋率对框架结构抵抗冲击作用更有效。在冲击作用下,各层柱顶水平位移均经历了先向外然后向内运动过程,表明各层框架梁的受力过程均经历了明显的拱效应和悬索效应阶段,且每层梁的受力过程接近,但随着冲击能量的增大,拱效应与悬索效应更加明显。

图11 三层框架结构响应时程曲线
3.3.3 抗倒塌能力分析
表5给出了各冲击高度下四个框架的抗连续倒塌能力,由表5和图12可知,冲击高度与结构发生连续倒塌所需的冲击能量之间满足指数关系,图中12给出了3-A、3-B框架的曲线拟合公式,3-C、3-D框架与3-B框架很接近,未重复给出。由图12可知,3-B、3-C、3-D三个框架的抗连续倒塌能力相当,3-A框架抗连续倒塌能力相对较低,约相当于其60%,这表明,增强框架梁的抗弯能力能够显著提高框架结构的抗连续倒塌能力。图13给出了部分工况下各框架各层梁反力和中柱竖向位移的关系曲线。由图13可知,3-A框架三层框架梁的内力很接近,3-B、3-C、3-D三榀框架配筋率高的楼层内力较大,其耗能能力相对较强,其余各层梁的内力与3-A框架接近,其耗能能力相对较弱。从以上分析可知,对于多层钢筋混凝土框架,针对任何一层框架梁的抗弯能力或者加固处理措施进行相同程度的增强,整体结构在冲击荷载作用下的抗连续倒塌能力效果是相当的。因此,为了提高框架结构在冲击荷载作用下的抗连续倒塌能力,可以适当提高失效柱上部框架梁中受弯钢筋的配筋率以及配箍率,特别是底部框架梁的加强,对于已建建筑结构,采用粘钢法来加强其框架梁对于其抗冲击作用较为有效。
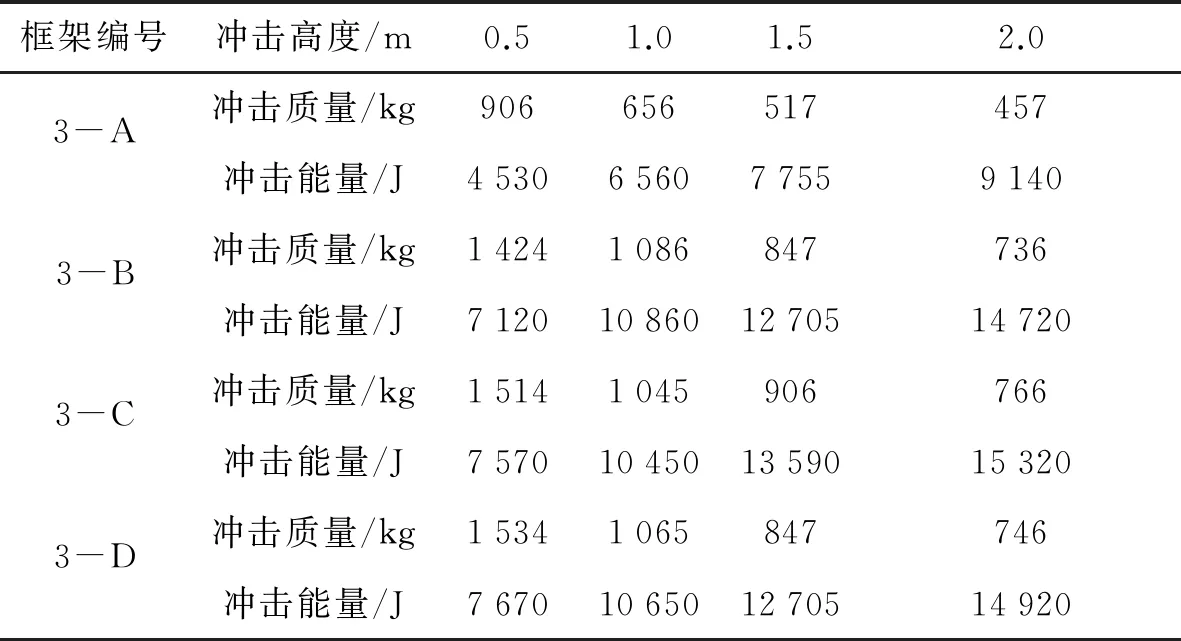
表5 三层框架抗连续倒塌能力
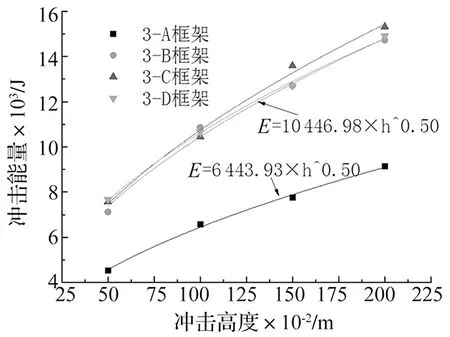
图12 抗连续倒塌能力-冲击高度曲线

图13 框架梁内力-竖向位移曲线
4 结 论
(1)本文采用的用于模拟冲击作用过程的LS-DYNA数值计算参数能够较好反应钢筋混凝土梁在冲击作用下的受力过程与破坏形态,计算结果与文献试验结果吻合较好。
(2)框架梁在冲击荷载作用下经历了明显的拱效应和悬索效应受力过程,随着冲击能量的增大,其效应更加明显,与静力加载过程类似,随着纵筋配筋率的降低其拱效应也越明显。梁端反力(剪力之和)可以较好反映框架的抗冲击承载能力,由于框架结构的空腹作用,三层框架承载能力提高幅度相对于单层框架结构有所提高,且随着框架梁配筋率的增大其承载能力也在提高。
(3)框架梁的抗弯钢筋断裂前,增大各层框架梁配筋率能显著提高框架的变形能力,受拉钢筋完全断裂后,各框架的竖向位移迅速增加,且提高底层框架梁配筋率对框架结构抵抗冲击作用更有效。
(4)对于多层平面框架,配筋率高的框架梁所承受的荷载相对较大,为提高其在冲击荷载作用下的抗连续倒塌能力,对其任何一层进行同等强度的加强均可以得到相同的效果,但提高底层框架梁承载能力,可以充分发挥材料性能。
(5)随着冲击高度的增加,使结构发生连续倒塌所需的临界冲击能量也增加,冲击能量与冲击高度呈指数关系变化。这主要是由于冲击高度的增加导致结构发生连续倒塌所需的临界冲击质量降低,冲击质量越低,冲击过程中的能量损失越大。
[ 1 ] PEARSON C, DELATTE N. Ronan point apartment tower collapse and its effect on building codes[J]. Journal of Performance of Constructed Facilities, 2005, 19(2): 172-177.
[ 2 ] BYFIELD M, PARAMASIVAM S. Murrah Building Collapse: Reassessment of the transfer girder[J]. Journal of Performance of Constructed Facilities, 2012, 26(4): 371-376.
[ 3 ] ZDENFK P, BAZANT. Mechanics of progressive collapse: Learning from world trade center and building demolitions[J]. Journal of Performance of Constructed Facilitics, 2007, 133(3): 308-319.
[ 4 ] KANG H, KIM J. Progressive collapse of steel moment frames subjected to vehicle impact[J]. Journal of Performance of Constructed Facilities, 2014, 4(14): 1-11.
[ 5 ] STINGER S M, ORTON S L. Experimental evaluation of disproportionate collapse resistance in reinforced concrete frames[J]. ACI Structural Journal, 2013, 110(3): 521-529.
[ 6 ] QIAN K, LI B. Analytical evaluation of the vulnerability of RC frames for progressive collapse caused by the loss of a corner column[J]. Journal of Performance of Constructed Facilities, 2013, 29: 1-14.
[ 7 ] YI W J, HE Q F, XIAO Y, et al. Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structures[J]. ACI Structural Journal, 2008, 105(4):433-439.
[ 8 ] 李易,叶列平,陆新征. 基于能量方法的RC框架结构连续倒塌抗力需求分析Ⅰ:梁机制[J].建筑结构学报, 2011,32(11):1-8. LI Yi, YE Lieping, LU Xinzheng. Progressive collapse resitance demand of RC frame structures based on energy method I:beam mechanism[J]. Journal of Building Structures,2011,32(11):1-8.
[ 9 ] 苏幼坡,张玉敏,许琳琳,等. 突加荷载作用下钢筋混凝土框架梁性能试验研究[J].建筑结构学报,2009,17(增刊2):92-97. SU Youpo, ZHANG Yumin, XU Linlin, et al. Experimental research of reinforced concrete frame beam under a sudden load[J]. Journal of Building Structures,2009,17(Sup2):92-97.
[10] KISHI N, NAKANO O, MATSUOKA K G, et al. Experimental study on ultimate strength of flexural-failure-type RC beams under impact loading[C]//In: Transactions of the 16th International Conference on Structural Mechanics in Reactor Technology (SMIRT). Washington DC, 2001: 15-20.
[11] KISHI N, MIKAMI H, MATSUOKA K G, et al. Impact behavior of shear-failure-type RC beams without shear rebar[J]. International Journal of Impact Engineering, 2002, 27(9): 955-968.
[12] KISHI N, MIKAMI H, ANDO T. Impact-resistant behaviour of shear-failure-type RC beams under falling-weight impact loading[C]// In: Proceedings of the 7th International Conference on Structures under Shock and Impact. Ashurst Lodge, 2002: 499-508.
[13] 赵德博, 易伟建. 钢筋混凝土梁抗冲击性能和设计方法研究[J]. 振动与冲击, 2015, 34(11): 139-145. ZHAO Debo,YI Weijian. Anti-impact behavior and design method for RC beams[J].Journal of Vibration and Shock, 2015, 34(11): 139-145.
[14] 何庆锋, 刘义仁, 蒋曲翀, 等. 锤击荷载作用下钢筋混凝土框架连续倒塌性能试验研究[J]. 湖南大学学报(自然科学版),2015,42(1):40-46. HE Qingfeng,LIU Yiren,JIANG Quchong,et al. Experimental study of the collapse performance of RC frame under hammer load[J]. Journal of Hunan University(Natural Science),2015,42(1):40-46.
[15] GUO Wenjun, GILSANZ Romon. Nonlinear static analysis procedure-progressive collapse evaluation[C]//Design Engineers of Gilsanz Murray Steficek, 2003: 15-20.
[16] SOLEIMANI S M, BANTHIA N, MINDESS S. Behavior of RC beams under impact loading: some new findings[C]// In: Proceedings of the Sixth International Conference on Fracture Mechanics of Concrete and Concrete Structures. London, 2007: 867-874.
Numerical simulation for progressive collapse of a reinforced concrete frame under impact load
HE Qingfeng, LIU Yiren, ZHOU Chao, YI Weijian
(College of Civil Engineering, Hunan University, Changsha 410082, China)
In order to study the collapse-resistant behavior of a RC frame under impact load, here, numerical simulation analyses for two 1-story and four 3-story RC frame models under impact load were conducted using the finite element software LS-DYNA.The major variable in analyses is longitudinal reinforcement ratio. The results showed that each frame beam has experienced the obvious arch effect and catenary effect under impact load; in addition, the arch effect become more obvious with decrease in reinforcement ratio; the reinforcement ratio also has an influence on the collapse-resistant ability of the frame, the higher reinforcement ratio can result in relatively strong load-bearing and energy-dissipation capacity of the frame, and the vierendeel effect of the frame can improve the load-bearing capacity of multi-story frame structures. Based on the results of numerical calculation, the collapse-resistant ability of RC frames was analyzed, and some strengthening measures were proposed accordingly.
progressive collapse; collapse-resistant design; impact load; LS-DYNA numerical simulation
国家自然科学基金(51108170);中央高校基本科研业务费;国家重点专项(2016YFC0701400)
2015-10-10 修改稿收到日期:2015-12-09
何庆锋 男,博士,高级工程师,1977年生
易伟建 男,博士,教授,博士生导师,1954年生
TU746.5
