基于弹性转角分离的非圆齿轮扭振模型及其动态特性

刘大伟， 任廷志, 巴延博， 谷丹丹， 杨二旭

(燕山大学 机械工程学院，秦皇岛 066004)

基于弹性转角分离的非圆齿轮扭振模型及其动态特性

刘大伟， 任廷志, 巴延博， 谷丹丹， 杨二旭

(燕山大学 机械工程学院，秦皇岛 066004)

随着非圆齿轮向高速重载应用领域的扩展，其动力学问题日益凸显，针对非圆齿轮的非线性转角关系，提出基于弹性转角分离的动力学建模方法。首先根据非圆齿轮传动特征，分析其内部激励产生机理并给出非圆齿轮自身特有激励的计算方法；以非圆齿轮弹性转角为自变量，考虑时变刚度，阻尼，误差及非圆齿轮特有的非线性激励，根据集中参数理论建立了非圆齿轮的扭振模型；最后以椭圆齿轮为例，应用高精度Rounge-Kutta法，定量地研究了不同工作条件下，不同激励对振动响应的影响规律。研究成果对于认识和改善非圆齿轮复杂的动态性能具有重要的理论意义和实用价值。

非圆齿轮；参数激励；扭转振动；动态响应

非圆齿轮是一种紧凑而精确的变速比传动机构，在很多设备中采用非圆齿轮，可以大大简化机构的复杂程度，提高设备的性能，另外非圆齿轮在主动平抑传动系统的速度及扭矩波动方面上也展现出独特的优势，故其应用从低速轻载领域逐步扩展到高速重载领域，如连铸机结晶器驱动装置[1]，旋转叶片发动机[2]和火炮旋转平台[3]，随着非圆齿轮的广泛应用，非圆齿轮动力学特性已成为制约其应用关键问题。

由于变速比传动的特点，非圆齿轮相对圆齿轮具有更多的非线性激励因素，故其动力学更为复杂。LIU等[4-5]通过试验对椭圆齿轮振动和噪声进行了测试，并分析了不同外部条件下的齿轮振动规律；在理论研究方面，王艾伦等[6]基于键合图理论建立了椭圆齿轮的扭转-轴向耦合模型，认为惯性力和离心力是造成振动的主要原因，却没有关注时变的节曲线向径所造成的影响；张爱梅等[7]将非圆齿轮在圆周上分段，在每段上用圆齿轮代替，但建模时忽略了非圆齿轮由于变速比传动导致的惯性力；LIU等[8]将惯性力作为等效负载，以各齿轮对电机的相对转角为自变量建立了非圆齿轮-转子扭振模型，不过在描述轮齿间相对位移时忽略了非圆齿轮的非线性转角关系；李宪奎等[9-10]分析了椭圆齿轮驱动结晶器运动时产生的低频共振现象，但模型中没有考虑椭圆齿轮轮齿间的弹性变形。上述研究对非圆齿轮理论的发展具有积极的推进作用，但由于非圆齿轮非线性激励较多的缘故，现有模型都进行了部分简化，无法较全面准确地反映非圆齿轮的动态性能，因此在详细分析非圆齿轮内部激励产生机理的基础上，建立了基于弹性转角分离的非圆齿轮的扭转振动数学模型，对不同激励下非圆齿轮的动态响应规律进行研究，并根据响应特点给出了提高非圆齿轮动态性能的有效方法。

1 非圆齿轮的内部激励

1.1 内部激励的类型

非圆齿轮可以看作是凸轮与齿轮组合体，在传动中，其内部激励不仅包含常规圆齿轮的刚度激励，误差激励和啮合冲击激励，而且由于时变传动比的影响，非圆齿轮还具有另外两种特殊的内部激励。

图1给出了一对非圆齿轮节曲线在两个时刻的位置关系;其中点P为非圆齿轮的节点;直线mm为节点P处两节曲线的公切线;直线nn代表齿廓接触点的法线;a0为加工刀具的齿形角。过非圆齿轮的回转中心O1，O2，作法线nn的垂线，可分别得到该时刻两个非圆齿轮啮合力的力臂rb1和rb2。

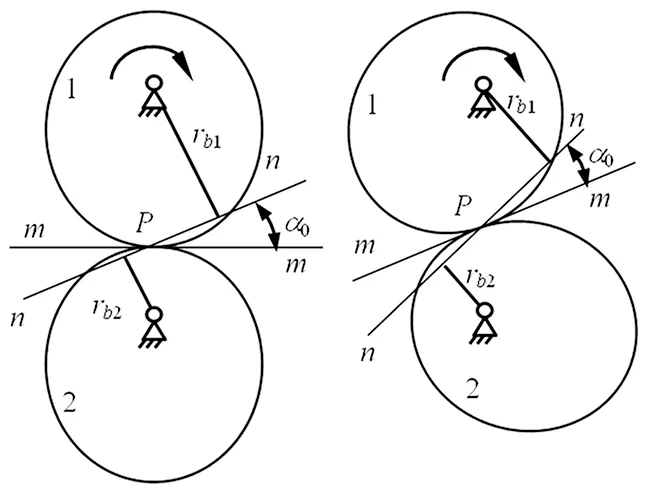
图1 不同时刻的非圆齿轮

从图1可知，在非圆齿轮传动的不同时刻，其节点位置，法线方向以及啮合力力臂都是变化的，即使外载不变，两非圆齿轮齿廓啮合力大小和方向也会随时间变化，从而产生激励。这种激励产生的根本原因在于非匀速传动比使非圆齿轮的啮合力力臂具有时变性。在不考虑其它激励的情况下，非圆齿轮也会由周期变化的啮合力力臂产生弹性振动，故其属于一种参数激励。

另外，由于非圆齿轮从动轮变速转动，从动轮及其连接机构会产生额外惯性力，该惯性力与负载综合作用，对非圆齿轮中的从动轮产生一种类似周期性外部激励效果。但本质上，惯性力是由非圆齿轮的传动特性决定，因此惯性力激励也是一种内部参数激励。

1.2 内部激励的计算方法

非圆齿轮的刚度激励，误差激励和啮合冲击激励可参照常规圆形齿轮的计算方法，但非圆齿轮的轮齿形状不规则，而且各不相同，不易通过理论计算得到精确的轮齿刚度，因此可采用有限元法。

首先应根据齿廓数学方程求出齿廓曲线数据，导入有限元软件建立非圆齿轮的轮齿模型，对单个轮齿进行网格划分，施加齿面法向载荷F以及定义边界等预处理，如图2(a)所示。通过计算得到轮齿的变形量如图2(b)，经多次计算发现，啮合线处的位移最大而且数值随网格的疏密程度变化。啮合线附近位移量大是因为该处除了弯曲变形外还有接触变形，而数值随网格变化是因为载荷施加点处出现奇异值。为了得到较为准确的轮齿变形量，可以采集啮合线以及啮合线附近区域的变形数据，取其平均值作为该受力方向上轮齿的变形量s，将平均变形量代入k=F/s，即可求出该啮合线处的单齿刚度k。改变轮齿啮合线位置，计算不同啮合点处轮齿刚度，将所得的数据进行拟合，可得单齿刚度曲线。同理可计算出另一个非圆齿轮上之配合的轮齿刚度曲线，将两个轮齿按串接弹簧处理，得到单对轮齿啮合刚度曲线。

图2 单齿有限元模型

按上述方法可得非圆齿轮副其它单对轮齿的啮合刚度，然后根据啮合过程单、双对轮齿的交替规律，计算出非圆齿轮在整个回转周期内的综合刚度km1，如图3所示。与圆齿轮不同的是，非圆齿轮单齿啮合刚度及单、双齿啮合区间不是固定的，因此若要得到精确的综合刚度，需要计算出所有轮齿的单齿刚度及相应的单、双齿啮合区间。

图3 轮齿综合刚度曲线

非圆齿轮的啮合力力臂不仅与节曲线的形状有关，而且还与非圆齿轮的转动方向有关。图4给出了一对非圆齿轮在同一位置转动方向不同时的啮合力力臂简图。若主动齿轮1顺时针旋转，如图4(a)所示，非圆齿轮的右齿廓接触，此时非圆齿轮啮合力力臂为

(1)

式中:r1、r2分别为两非圆齿轮在节点P处的节曲线向径;m为节点P处节曲线切线与向径的夹角;其表达式为:

(2)

式中:φ1为非圆齿轮1节曲线的极角，若非圆齿轮从极角为零时开始旋转，则非圆齿轮的极角和转角相等。为便于表示，下文推导中非圆齿轮的极角与转角均相等。

若主动齿轮1逆时针旋转，如图4(b)所示，非圆齿轮的左齿廓接触，此时非圆齿轮的啮合力力臂为

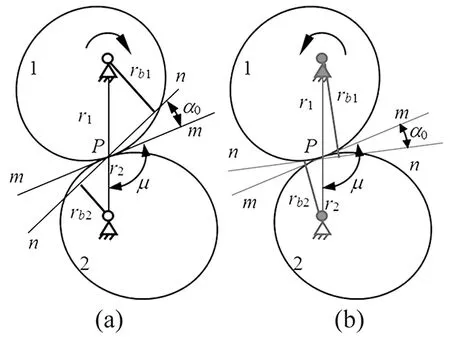
图4 非圆齿轮的啮合力力臂

(3)

惯性力激励计算可根据主动轮的转速和非圆齿轮的传动比算出从动轮的角速度，对其求时间的导数可得从动轮角加速度，然后与从动齿轮及负载的转动惯量之和相乘可得惯性力。

2 非圆齿轮的扭转振动模型

齿轮的扭转振动模型是齿轮系统动力学的基础，因此针对非圆齿轮最基本的扭转振动形式展开研究。在任意瞬时，将非圆齿轮等效成半径为rb1和rb2的集中转动惯量元件，如图5中虚线所示，其转动惯量不随半径变化。非圆齿轮的轮齿等效成弹簧和阻尼器，在任意瞬时其方向与齿廓法线相同。

图5 非圆齿轮的扭转模型

由于非圆齿轮转角间的非线性关系，两齿轮在齿廓法线上的相对位移不能像圆齿轮一样表示成x=rb1φ1-rb2φ2，而应表示成

(4)

式中:φ1、φ2为非圆齿轮1和非圆齿轮2的转角；i12为非圆齿轮1和非圆齿轮2的角速度之比。一般情况下，非圆齿轮传动比的积分运算无法获取解析函数，那么利用式(4)建立的非圆齿轮扭振微分方程中还包含积分项，其求解相当困难，因此基于弹性转角分离原理，提出了一种简单的非圆齿轮动力学模型构建方法，便于数学方程推导和求解。

2.1 非圆齿轮副扭振模型

将非圆齿轮作为弹性机构时，其真实转角φ可以看成是刚性转角和弹性转角之和。令图5中非圆齿轮1的真实转角、刚性转角和弹性转角分别为φ1、θ1和Δθ1，非圆齿轮2的真实转角、刚性转角和弹性转角分别为φ2、θ2和Δθ2。

由于刚性转动时，非圆齿轮在节点处的相对转速为零，故非圆齿轮在齿形法线上的相对移动都是由弹性转角所致，而与刚性转角无关。考虑到齿轮的弹性转角很小，可认为在t时刻，虽然齿轮发生弹性转动，但啮合力方向不变，即rb1和rb2不变。故非圆齿轮等效弹簧的位移为

x=rb1Δθ1-rb2Δθ2

(5)

式中:x为等效弹簧的位移;在t时刻，非圆齿轮等效阻尼器的速度为

(7)式中:I1，I2分别为非圆齿轮1和非圆齿轮2的转动惯量;非圆齿轮1的刚性速度可以是恒定的也可以是变化的。不考虑非圆齿轮齿侧间隙，根据非圆齿轮1和非圆齿轮2所受扭矩平衡，可得非圆齿轮副的扭振方程为

(8)

式中:km1，cm1分别为非圆齿轮副的综合啮合刚度和阻尼;e1为轮齿综合误差;T1为齿轮副的驱动力矩;T2为齿轮副的阻力矩。方程中弹性转角为未知参数，而刚性角加速度可根据传动机构的刚性角速度及结构参数进行求解。

2.2 非圆齿轮-转子扭振模型

在非圆齿轮副纯扭振模型基础上，考虑传动轴的扭转刚度以及原动机和负载的转动惯量，则形成齿轮-转子扭振问题，其典型的模型见图6。

图6 非圆齿轮-转子扭转模型

弹性转角分离原理同样适用传动轴上的扭矩求解，对于图6中的传动轴1，电机转动惯量和非圆齿轮1之间的扭矩可由二者的弹性转角表示为k1(ΔθM-Δθ1)，则整个传动系统的模型为

式中:IM、IL为电机和负载的转动惯量;k1、c1为电机与主动非圆齿轮连接轴的扭转刚度和扭转阻尼;k2、c2分别从动非圆齿轮与负载连接轴的扭转刚度和扭转阻尼;TM、TL为作用在原动机和负载上的扭矩;θM、θL为原动机和负载的刚性转角;ΔθM、ΔθL为原动机和负载的弹性转角。

3 非圆齿轮的扭振特性分析

非圆齿轮扭振方程为二阶线性变系数微分方程，相比圆齿轮动力学模型增加了时变的啮合力力臂和惯性力激励，通过解析方法求解比较困难，故本文应用Rounge-Kutta法求解高精度数值解。

为了更加直接的反映非圆齿轮的动态特性，不考虑误差影响，应用齿轮副模型，计算一对椭圆齿轮的动态响应，其中椭圆齿轮传动比为

(10)

式中:ε为偏心率，0<ε<1。椭圆齿轮的模数m=6 mm，刀具齿形角α0=20°，齿数Z=56。通过有限元计算，得到椭圆齿轮副刚度曲线见图7，齿轮的阻尼cm1为

(11)

式中:ζ为阻尼比。

图7 非圆齿轮综合刚度曲线

3.1 不同偏心率下的动态响应

椭圆齿轮的偏心率控制其传动比，偏心率越大，椭圆齿轮的传动比范围越大，啮合力力臂和惯性力变化越剧烈。令椭圆齿轮主动轮角速度为40 rad/s，从动轮阻力矩为1 000 N·m，椭圆齿轮的偏心率分别取0.01，0.2和0.5，则根据ROUNGE-KUTTA法原理，在MATLAB中编程对微分方程式(8)进行数值计算，得到从动轮弹性转角时域响应曲线及相应的幅频曲线如图8所示。

图8中左侧的时域响应曲线表明，非圆齿轮的动态响应随着偏心率的增大而增大。但非圆齿轮不仅有轮齿刚度激励，还有啮合力力臂及惯性力激励，因此进一步通过频谱分析，探索这些非线性因素在振动中所起的作用。在本例中刚度激励的频率为365 Hz，啮合力力臂及惯性力激励频率与椭圆齿轮的传动比变化频率相同，都为6.4 Hz，在分析中难以区分二者，故将啮合力力臂和惯性力统称为传动比综合激励。

通过频谱分析发现，当椭圆齿轮偏心率较低时，如图8(a)中ε=0.1时，传动比综合激励频率6.4 Hz对应的振幅小于刚度激励频率365 Hz对应的振幅，故刚度激励是产生振动的主要原因；随这偏心率ε提高到0.2，如图8(b)所示，刚度激励与传动比综合激励频率对应的振幅接近，二者对齿轮振动的影响程度相当；在图8(c)中，偏心率ε提高到0.3，传动比综合激励频率对应的振幅超过刚度激励频率对应的振幅，传动比综合激励成为非圆齿轮振动的主要原因。因此对于大传动比范围的非圆齿轮来说，通过齿廓修形改善非圆齿轮动态性能的效果将不会很明显，此时应采用串联非圆齿轮的形式，将传动比分配到两对或多对非圆齿轮上，以此减小传动比综合激励引起的振动。

(a) ε=0.1 (b) ε=0.2 (c) ε=0.3

另外，随着椭圆齿轮偏心率的增大，刚度激励的振幅略有增加，传动比激励的振幅则大幅增加，说明对于轮齿刚度相近的一对非圆齿轮和一对圆齿轮，非圆齿轮的动态性能要比圆齿轮差。将本例中的椭圆齿轮与一对传动比为1，刚度相同的圆齿轮进行对比，椭圆齿轮偏心率为0.1，0.2和0.5时，其弹性转角最大幅值相对圆齿轮分别扩大了3.13倍，3.49倍和7.59倍。

3.2 不同输入转速下的动态响应

图9为从动轮阻力矩为1 000 N·m，偏心率为0.3，主动轮输入角速度分别为50 rad/s，100 rad/s和200 rad/s条件下椭圆齿轮的动态响应及相应的幅频曲线。从图9中的时域响应曲线可知，虽然转速增加会导致惯性力变大，但椭圆齿轮的动态响应幅值并没有随输入转速升高而一直增大。通过频谱分析可以发现：在偏心率不变的情况向，随着输入转速的升高，椭圆齿轮刚度激励和传动比综合激励引起的动态响应都在增加，但二者对应的振幅比值基本保持不变，因此输入转速不会改变刚度激励和传动比综合激励在齿轮振动中的主次作用。

(a) 50 rad/s (b) 100 rad/s (c) 200 rad/s

3.3 不同扭矩下的动态响应

图10为椭圆齿轮输入角速度为40 rad/s，偏心率为0.3，从动轮阻力矩分别为1 000 N·m，2 000 N·m和3 000 N·m时的动态响应及相应的幅频曲线。

(a) 阻力矩1 000 N·m (b) 阻力矩2 000 N·m (c) 阻力矩3 000 N·m

从图10中可以看出，随着阻力矩的增大，椭圆齿轮的动态响应近似呈线性增加，这与圆齿轮是相同的，因此阻力矩也无法改变刚度激励和传动比综合激励在齿轮振动中所起的主次作用。对于小偏心率的动力非圆齿轮，可通过适当修形改善其动态性能，而对大偏心率的动力非圆齿轮，宜采用多对串联非圆齿轮替代的方式以提高传动系统的动态性能。

4 结 论

(1)将非圆齿轮弹性转角从总转角中分离，进而通过集中参数理论构建非圆齿轮动力学模型，不仅能有效避免非线性刚性转角给建模及求解带来的困难，而且可准确反映出非圆齿轮所特有的啮合力力臂及惯性力激励，同时该方法也可推广到非圆齿轮耦合动力学的研究中。

(2)非圆齿轮的传动比综合激励随偏心率的增大会逐渐超越刚度激励而成为非圆齿轮振动的主要原因。随着非圆齿轮转速和负载扭矩的增大，传动比综合激励及刚度激励所引起的动态响应都会增加，但并不改变二者在非圆齿轮振动中的主次作用，因此对于高速、重载非圆齿轮，应根据偏心率的大小，来确定改善其动态性能的有效方法。

[ 1 ] 刘大伟，任廷志. 非圆齿轮驱动结晶器非正弦振动的研究[J]. 中国机械工程，2013，24(3)：327-331. LIU Dawei, REN Tingzhi. Research on nonsinusoidal oscillation of mold driven by noncircular gears [J]. China Mechanical Engineering, 2013, 24(3): 327-331.

[ 2 ] TUCKER R W, WANG C, LIBROVICH B V. Mathematical modeling of rotary vane engines [J]. Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science, 2003, 217(6): 687-704.

[ 3 ] 高颖，王惠源，张鹏军. 非圆齿轮传动系统在优化转管武器功耗方面的应用[J]. 火炮发射与控制学报，2014，35(1)：40-43. GAO Ying, WANG Huiyuan, ZHANG Pengjun.The application of non-circular gear in optimizing the driving power of gatling gun [J]. Journal of Gun Launch and Control, 2014, 35(1): 40-43.

[ 4 ] LIU Xing, NAGAMURA Kazuteru, IKEJO Kiyotaka. Analysis of the dynamic characteristics of elliptical gears [J]. Journal of Advanced Mechanical Design，Systems and Manufacturing，2012, 6(4): 484-497.

[ 5 ] LIU Xing, NAGAMURA Kazuteru，IKEJO Kiyotaka. Vibration and noise characteristics of elliptical gears due to non-uniform rotation [J]. Journal of Advanced Mechanical Design，Systems and Manufacturing，2012, 6(4): 484-511.

[ 6 ] 王艾伦，马 强，刘琳琳. 椭圆齿轮动态特性仿真研究[J]. 机械传动，2006，30(4)：7-10. WANG Ailun, MA Qiang, LIU Linlin. Modeling and simulation of elliptical gears [J]. Journal of Mechanical Transmission, 2006, 30(4): 7-10.

[ 7 ] 张爱梅，蒋佳，魏丽君,等. 非圆齿轮的动力学特性研究[J]. 机械传动，2009，33(5)：20-23. ZHANG Aimei, JIANG Jia, WEI Lijun, et al. Study on dynamic characteristics of non-circular gear [J]. Journal of Mechanical Transmission, 2009, 33(5): 20-23.

[ 8 ] LIU Xing，NAGAMURA Kazuteru，IKEJO Kiyotaka. Simulation on the vibration characteristics of elliptical gears [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science，2012，227(4)：819-830.

[ 9 ] 李宪奎，杨红普，杨拉道. 椭圆齿轮驱动的结晶器低频共振分析[J]. 机械工程学报，2008，44(5)：231-237. LI Xiankui, YANG Hongpu, YANG Ladao. Low-frequencyresonance of mold driven by oval gears [J]. Chines Journal of Mechanical Engineering, 2008, 44(5): 231-237.

[10] 杨红普，李宪奎，张兴中,等. 结晶器非正弦谐波共振[J]. 机械工程学报，2007，43(7)：207-212. YANG Hongpu, LI Xiankui, ZHANG Xingzhong, et al. Harmonic resonance in non-sinusoidal oscillation of mold [J]. Chines Journal of Mechanical Engineering, 2007,43(7): 207-212.

Torsional vibration model and its dynamic characteristics for a noncircular gear based on separation of elastic rotating angle

LIU Dawei, REN Tingzhi, BA Yanbo, GU Dandan, YANG Erxu

(College of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China)

With the development of application of noncircular gears in high speed and heavy load field, their dynamic problems increasingly stand out. Aiming at the nonlinear ratating angle relationship of noncircular gears, a dynamic modeling approach was presented based on separation of elastic rotating angle. Firstly, according to transmission features of noncircular gears, the generation mechanism of the internal excitation was analyzed, the calculation method for itself special excitation of a noncircular gear was derived. Then based on the lumped parameter theory, the torsional vibration model for a noncircular gear was built with its elastic rotating angle as an independent variable considering time-varying stiffness, meshing damping, teeth error and the special nonlinear excitation of noncircular gears. Finally, with the high accuracy Rounge-Kutta method, the effect laws of internal excitations of a pair of elliptical gears on their dynamic responses were investigated under different working conditions quantitatively. The results were significant theoretically and valuable applicably for understanding and improving complicated dynamic characteristics of noncircular gears.

noncircular gear; parametric excitation; torsional vibration; dynamic response

河北省自然科学基金(E2016203183)；秦皇岛市科技支撑计划项目(201502A014)；燕山大学博士基金(B870)

2015-09-09 修改稿收到日期：2015-11-17

刘大伟 男，博士，讲师，1984年生

TH113.1