保证智能轮椅平滑通过狭窄通道的路径曲率优化算法

陈灵 王森 胡豁生 麦当劳-麦尔克劳斯 费敏锐

保证智能轮椅平滑通过狭窄通道的路径曲率优化算法

陈灵1王森2胡豁生3麦当劳-麦尔·克劳斯3费敏锐1

为了使用户更感舒适，智能轮椅应该能在具有复杂几何约束的室内环境下平滑地通过狭窄通道.本文提出一个基于路径曲率优化的算法以确保智能轮椅平滑地通过狭窄过道.考虑到路径平滑度取决于路径曲率及其变化率，在通过传感器数据计算出狭窄通道相对于轮椅的位置后，算法以贝塞尔曲线的曲率及其变化率最小为优化目标，以轮椅过通道时的方向及贝塞尔多边形应为凸多边形作为约束，规划出一条平滑的最优路径，然后控制轮椅实时跟踪这条路径.上述过程动态循环运行，实现了智能轮椅平滑通过狭窄通道.仿真中将本文算法同基于A*的路径规划导航算法进行了对比，结果表明本文提出的基于曲率优化的算法可以实现比A*算法路径曲率更小且更加平滑的过狭窄通道过程,并且即使在没有全局地图和定位信息情况下，算法也能控制轮椅平滑地通过狭窄过道.实验中详细阐述了算法的实现过程，实验结果也证实了算法的有效性.

智能轮椅,曲率优化,贝塞尔曲线,过通道

DOI10.16383/j.aas.2016.c160185

室内环境往往具有很多狭窄的过道,这给轮椅的正常工作带来较大挑战.另一方面,轮椅用户通常是行动不便者和老人,他们不能很好地控制轮椅.因此,一个巨大的需求在于智能轮椅能自动穿过较窄的过道,以便轮椅用户能感到安全和舒适[1].

智能轮椅过通道很大程度上依赖于其运动控制算法,可以分为两个部分:路径规划[2−5]和运动导航[6−7].路径规划用于计算一条穿过狭窄通道的可行的路径而不碰撞障碍物.传统的路径规划算法,如A*[8−9]和它的变体FHD*[10]运用优化的方法去找最短的避障路径.尽管这些算法已经成功用于通用移动机器人,它们却不能直接用于智能轮椅上而规划一条穿过狭窄通道的平滑路径,因为它们没有考虑环境的物理空间限制和用户舒适度.

由于通道宽度与轮椅宽度的比值较小(如英国标准研究院[11]所规定的,轮椅两边与通道墙之间只有300mm.图1(a)展示了在作者实验室里的相同的情况,留给轮椅通过过道的空隙两边共只有26cm),对轮椅来说很难使其在任意的航向角位置通过狭窄的门,如图1(b)所示,只有当轮椅的航向角垂直于门线时轮椅才能通过.而对于这样的物理空间的约束以及如何在此约束中平滑地通过通道,许多有关研究文献并没有考虑到.如Cheein等在文献[12]提出一种整合同时定位与地图构建算法的边界点方法用于轮椅通过过道.然而,它需要连续地产生平均边界点,从而使得轮椅的轨迹不平滑而且耗时.Peula等[13]提出基于案例推理的轮椅通过过道的方法,同样地,其也没有考虑规划路径的平滑性.

路径的平滑性一定程度上决定了轮椅用户在轮椅过狭窄通道时的舒适性,因此研究者提出了其他考虑路径平滑性的路径规划方法,如基于圆弧[14−15]、样条[1,16]和贝塞尔曲线[17−20]的方法.文献[1]提出基于B样条的方法,让一台仿真轮椅在仿真环境中通过一个狭窄的通道,而并没用真实轮椅进行测试.另外,文献[17]提出基于贝塞尔曲线的路径规划方法,用于一般的移动机器人,Choi等[21]也将类似方法用于自主驾驶汽车上,其约束由航路点和过道宽度产生.同样地,这些方法很难直接用在智能轮椅上.

本文提出一个基于路径曲率优化的算法以确保智能轮椅平滑地通过狭窄过道.算法以三次贝塞尔曲线的曲率及其变化率最小为优化目标,以通过传感器数据测得的过道相对于轮椅的位置、轮椅过通道时的方向及贝塞尔多边形应为凸多边形作为约束条件,实时计算满足优化目标和约束的三次贝塞尔曲线以作为期望路径,然后控制轮椅速度以跟踪此期望路径,从而实现轮椅光滑地通过狭窄通道的目的.相比于传统的A*算法及其变体,本算法使轮椅通过通道时路径更加平滑;而相比于其他考虑平滑性的路径规划方法,由于本算法利用在线测得的通道位置实时计算期望路径,因此不需要构建全局地图以及基于地图的全局定位,本算法更加简单和更易实现.

1 过通道策略

1.1 问题描述

过狭窄通道的问题可以看作是一个路径规划的问题.本文方法的目的是首先基于曲率优化产生一个平滑路径,然后控制轮椅去跟踪它.只要产生的期望路径能平滑通过狭窄过道且轮椅能够精确地跟踪它,那么过狭窄通道的问题就能成功解决.选择轮椅上的某个点作为控制的参考点.为了实现过通道,算法策略应该满足以下要求:

1)轮椅的实际路径必须是优雅且平滑的,没有震荡和模棱两可的情形.

2)由于轮椅的几何约束,路径的曲率应该限制在某个范围内.

3)当轮椅到达狭窄过道位置时,其航向角应该垂直于狭窄过道的平面.

图2所示为轮椅过狭窄通道的原理描述.为了产生平滑的过通道的路径,需要考虑轮椅的几何特征和大小.检测过道位置的传感器所在位置或者后轮的中心可以选为操作点.因此两个本地坐标系分别由{WL}(虚线)和{WC}(实线)表示,它们的原点分别是为全局坐标系G下狭窄通道的中心位置.和分别为轮椅的当前与期望位置,以及它们相对应的航向角Hs和Hd.除非特别声明,全文所有的位置和航向角都是相对于坐标系{WC}的.

1.2 算法结构

图3为提出的轮椅过狭窄通道的算法结构图.算法主要有三个模块,分别是:通道定位、路径规划和轮椅控制.在通道定位模块中,采用激光测距仪或者3D摄像头(如微软Kinect传感器),可以检测出相对于轮椅坐标系的通道中间位置.一旦通道位置被精确找到,它就被路径规划模块用于通过曲率优化产生一条期望的贝塞尔曲线路径.在轮椅控制模块中,期望的路径与轮椅当前位置之间的误差输入到PID控制器计算出轮椅二轮的速度,从而控制轮椅跟踪这个路径.这个过程反复实时运行.

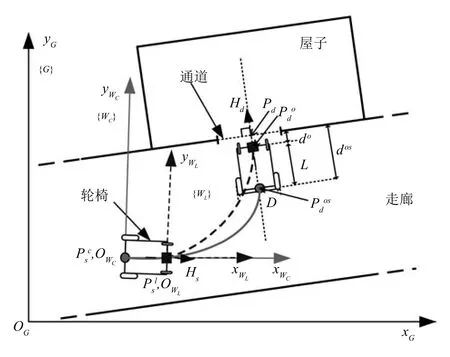
图2 轮椅过狭窄通道过程原理图Fig.2 The schematic description of the narrow gap passing process

每当检测到狭窄过道,算法动态产生一条平滑的路径,因此,过狭窄通道的策略可以连续不断进行而不需要里程计或者全局定位信息.这样可以大大减少来自轮椅和不确定环境带来的各种干扰,使得过狭窄通道过程更安全和有效.每个模块的详细描述如下.

1.2.1 通道定位

通道定位模块目的在于计算通道在轮椅坐标系里的相对位置(包括位置Pd和方向Hd,即过道法向量的方向),然后作为路径规划模块的输入.通道定位具体算法取决于所用的传感器类型.当使用二维激光测距仪时,结合分割和直线拟合的方法可以用来定位通道.后文实验部分将会详细介绍此方法.当使用深度摄像头时,红-绿-蓝颜色的图像数据首先通过分割算法被用于通道的识别,然后带有深度信息的深度图像用于精确找到通道相对于摄像头的位置.在摄像头的外部参数标定好的情况下,计算出来的结果可以很简单地通过平移旋转运算计算出通道相对于轮椅的位置.

1.2.2 路径规划

路径规划的目的在于采用优化方法确定贝塞尔曲线的控制点,使得由这些控制点决定的贝塞尔曲线路径具有最小的曲率变化率.最平滑的贝塞尔曲线满足各种来自轮椅和环境的约束.由于轮椅和过道之间的相对位置可实时计算得到,路径规划也连续不断地进行着.图2表示了弧线PsPd的控制点为Pi,i∈0,1,2,3,也就是三次贝塞尔曲线的控制点[21].

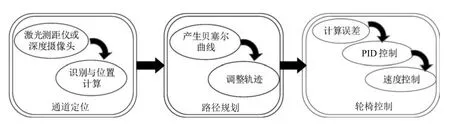
图3 轮椅过狭窄通道算法结构图Fig.3 Strategy architecture of narrow gap passing

然后,三次贝塞尔曲线便可生成,以连接点Ps和Pd,方向分别为Hs和Hd.也就是说,在检测到狭窄通道后,算法通过对贝塞尔曲线的曲率的优化,利用通道的中间点位置Ps及其对应的方向Hd进行控制点的计算.因为Ps和Pd分别已经对应了已知的控制点P0和P3,那么参数估计仅仅需要计算P1和P2,至此,在已知P0和P3情况下,整个贝塞尔曲线就被完全确定了.需要注意的是Hd期望是垂直于墙壁的.

为了满足前述的各项要求,根据环境和实际情况,为优化设计了两类约束:

1)方向.因为路径规划是从航向角Hs开始的,期望的贝塞尔曲线在位置P0处切线的斜率应该等于Hs.类似地,为了克服轮椅与通道宽度之间比值小的问题,点P3处的切线应该是通道的中间位置处的法向方向.因此,点P1和P2的可选范围进一步减小为一维.也就是说,由于贝塞尔曲线的第二个属性,点P1和P2必须分别处于点P0和P3的切线上.并且,P1需要沿着Hs的方向寻找,而P2只可能出现在Hd的反方向.因此,有关于方向的约束为

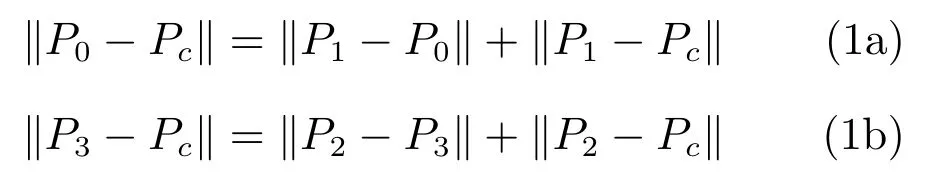
其中,Pc是直线P0P1和P2P3的交点,‖·‖表示二范数.这两个约束保证了由点P1和P2确定的贝塞尔曲线可以连接起点终点即P0和P3,并且对应的方向分别为Hs和Hd.

2)完全凸性.如前所述对曲率的约束要求曲线没有曲率的突然变化.于是,贝塞尔曲线必须是凸的.已经知道,如果贝塞尔曲线的控制点构成的多边形是凸的,那么贝塞尔曲线也呈完全凸性.因此,P1和P2必须在保证曲线的完全凸性的情况下进行约束.这里采用向量叉乘的方法来实现此约束.向量的叉乘ω1和ω2分别为

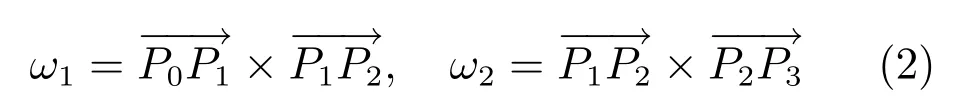
故而,完全凸性的约束表示为

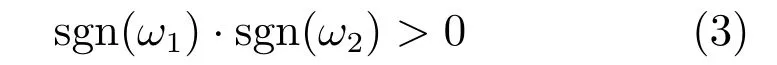
其中,sgn(ωi),i=1,2为向量ωi的旋转方向.

带约束的优化是为了找到控制点P1和P2使得曲线尽量光滑,也就是曲率及其变化率应当尽量小.由于这里只考虑二维环境,且为了平衡精度与算法复杂度,采用三次贝塞尔曲线,曲线坐标表示为B(t)=(x(t),y(t)),其中

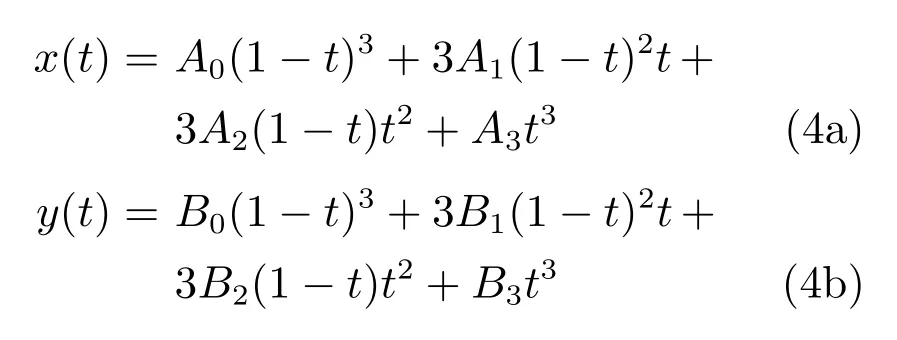
其中,(Ai,Bi)表示控制点Pi的坐标.那么贝塞尔曲线相对于变量t的曲率为

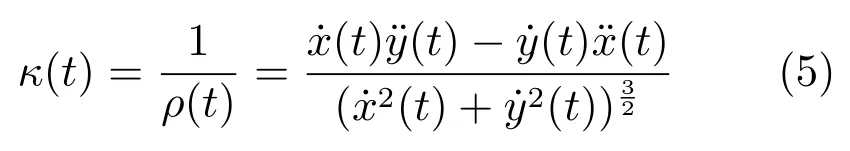
其中,ρ(t)为曲线半径.因此,P1和P2可由如下受约束于式(1)和式(3)的优化问题求得:

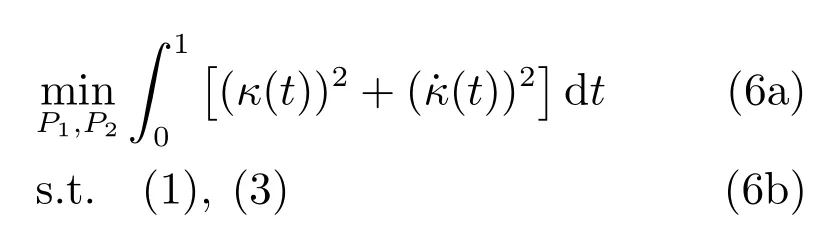
当轮椅到达狭窄的过道时,期望的轮椅航向角应该垂直于过道.但是由于干扰和控制的误差,最终的轮椅位置和方向可能有所偏离期望值.为了满足上述第3个要求,在轮椅通过过道前,轮椅的航向角必须调整为垂直于过道.

1.2.3 轮椅控制

为了使得轮椅能够跟踪规划好的路径,采用PID反馈控制器.轮椅实际的位置与参考路径之间的误差作为PID控制器的输入.如图4所示,沿着轮椅的航向角距离轮椅为Z的一点F用来定义位置误差,然后将点F投影到参考路径于点S,使得垂直于点S的切线.位置误差由点F和S之间的距离Derr表示.交叉跟踪误差Cerr由期望路径和轮椅重心位置(xr,yr)之间的最短距离表示.

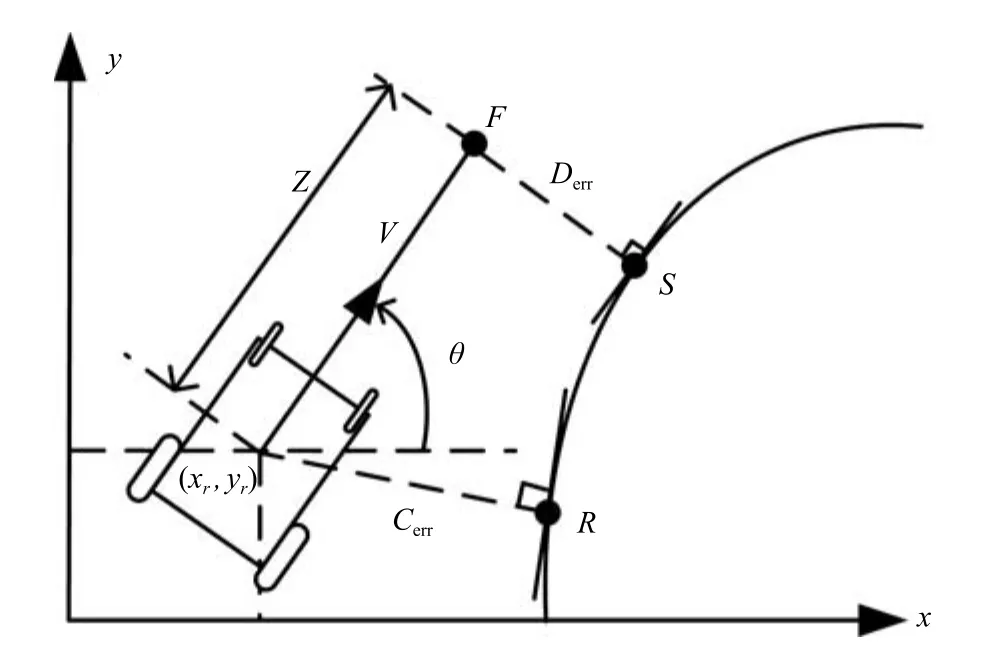
图4 位置误差的计算Fig.4 The calculation of the position error

在本文中,假定径向速度V为常量,角速度ω作为PID控制器的输出量.数字PID控制可以描述为

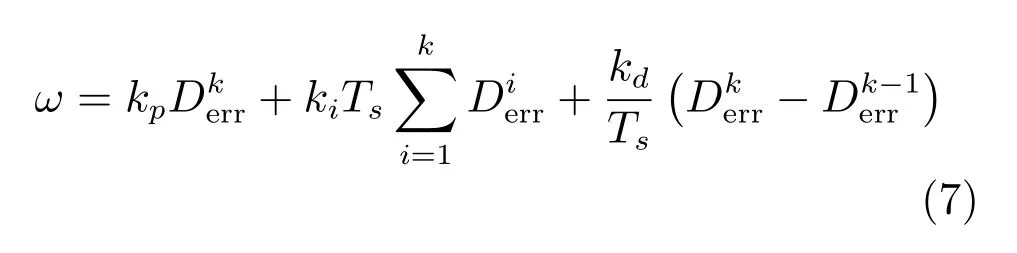
2 仿真和分析

2.1 仿真结果

首先,进行仿真来验证算法的核心部分,也就是基于贝塞尔曲线的曲率优化的路径规划算法.假设通道位置已知.进行了2种场景的仿真,分别为场景A(目标位置在通道左边)和场景B(目标位置在通道右边),如图5所示.

对于每一种情形,路径规划算法算出四个不同的最优参考轨迹.每一个参考路径对应不同的参数如轮椅的起始位置及其航向角,目标位置及其航向角.

表1列出了每一条参考路径对应的所需参数,其中,Ps,Pd和Pt分别表示轮椅在走廊里的起始坐标、通道中间点的坐标和在房间里的目标点位置坐标,单位为m.i(Hs,Hd)表示路径i的起始位置和通道中间位置对应的航向角(单位为度),i(Hd,Ht)表示路径i的通道中间位置和穿过通道之后的目标点位置对应的航向角.以路径1为例,对于场景A,对应轮椅的起始位姿由起始坐标Ps及航向角Hs构成,即(0.1,1.3,−20),终点位姿由通道中间点的坐标Pd及航向角Hd构成,即(1.6,1.8,90),路径2与路径1类似;再以路径3为例,对应轮椅的起始位姿由通道中间点的坐标Pd及航向角Hd构成,即(1.6, 1.8,90),终点位姿由目标点位置坐标Pt及航向角Ht构成,即(0.0,3.5,160),路径4与路径3类似.以这些参数作为输入,路径规划算法便可计算出平滑路径然后由PID控制器控制轮椅进行跟踪.PID控制器输出驱动轮椅行进的转速.控制器各系数选择为kp=0.01,ki=0.001和kd=0.001.

图5展示了计算出的参考路径及其对应的轮椅实际路径,各参考路径对应的参数如表1给出.由图5可以得出如下结论:

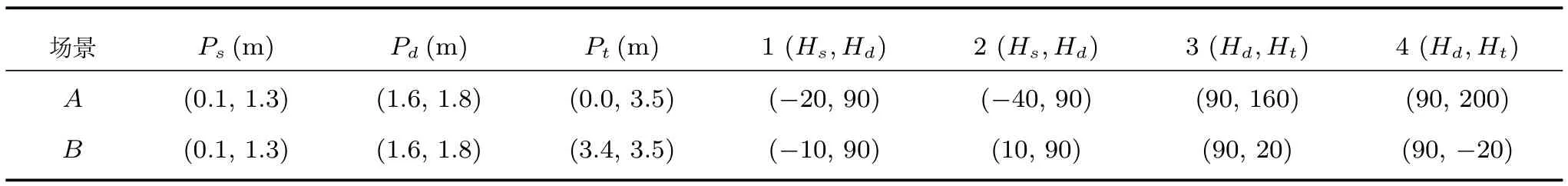
表1 每条路径的输入参数Table 1 The input parameters for each path

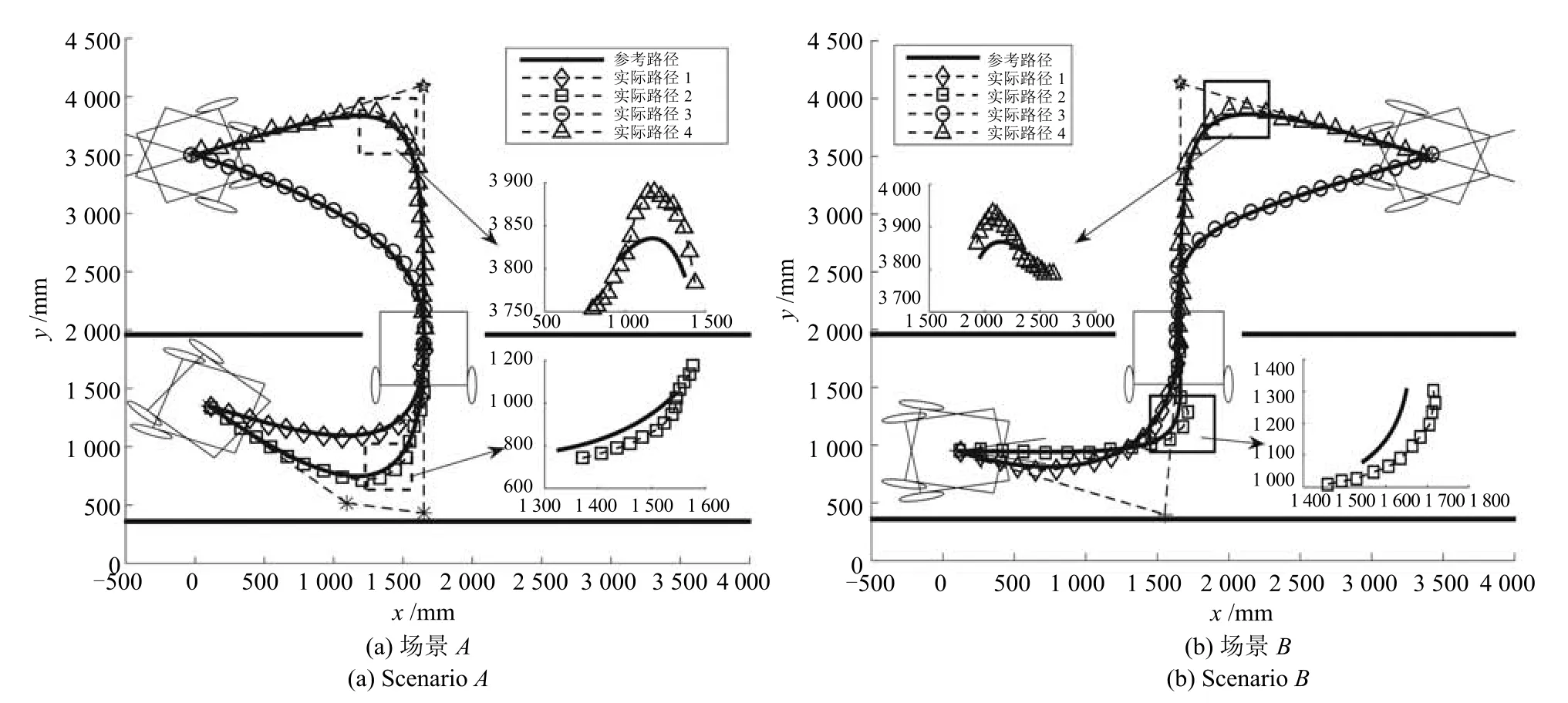
图5 轮椅的参考路径和实际路径Fig.5 Reference path and actual path of wheelchair

1)所有的最优参考路径满足在路径规划部分提到的约束:首先,轮椅始终在走廊里;其次,贝塞尔曲线在起始位置的切线方向等于轮椅的航向角,在目标位置也是如此;再次,计算出的贝塞尔控制多边形是凸的.

2)所有最优参考路径是平滑的.

3)尽管有小的跟踪误差(从图中放大部分可以看出),轮椅的实际轨迹能较精确地跟踪参考路径.

因此,仿真验证了过狭窄通道算法的有效性.

为了分析轮椅实际跟踪路径的平滑性和精确度,如图6(a)和图6(b)所示,分别展示了场景A仿真中的轮椅角速度ω和距离误差Derr相对于贝塞尔曲线参数t的变化曲线.由图6可知,角速度没有呈现出突变,表明了轮椅运动的平滑性.最大的跟踪误差约为55mm,都在合理和接受的范围,表明跟踪精度较高.

2.2 与其他算法的比较

为了验证本算法相对于其他主流室内路径规划算法的在过狭窄通道情况下的优越性,进行了另一个仿真以比较本文算法和基于A*[22]的开源算法在路径曲率(光滑度)上的表现.如图7所示,实验场景为包含2个80cm狭窄通道的室内环境,仿真平台为基于机器人操作系统(Robot operating system,ROS[23])的Gazebo[24]三维仿真器.仿真中,本文算法的核心部分在Matlab中运行,通过Matlab的Robotics工具箱可以实现与ROS和Gazebo系统的数据通信,一方面来自Gazebo中轮椅上的激光测距仪数据可以传入Matlab中通道定位模块,实现通道位置计算;另一方面Matlab中轮椅控制模块计算出的轮椅速度值可以发送给Gazebo中的轮椅,实现轮椅的控制.其中路径曲率优化算法采用Matlab优化工具箱中的内点法优化方法.而基于A*路径规划导航算法实现采用ROS的开源软件包Navigation Stack[25].仿真时,两种方法均控制轮椅从起点位姿(1.5m,0m,0rad)穿过2个狭窄通道并到达终点位姿(0.5m,3.5m,3.14rad),线速度设定为0.15m/s.其中位姿第3项表示轮椅的航向角.

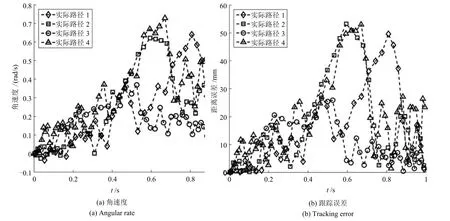
图6 在场景A中每一条路径对应的轮椅的角速度和跟踪误差Fig.6 The angular rate and the tracking errors for each path in ScenarioA

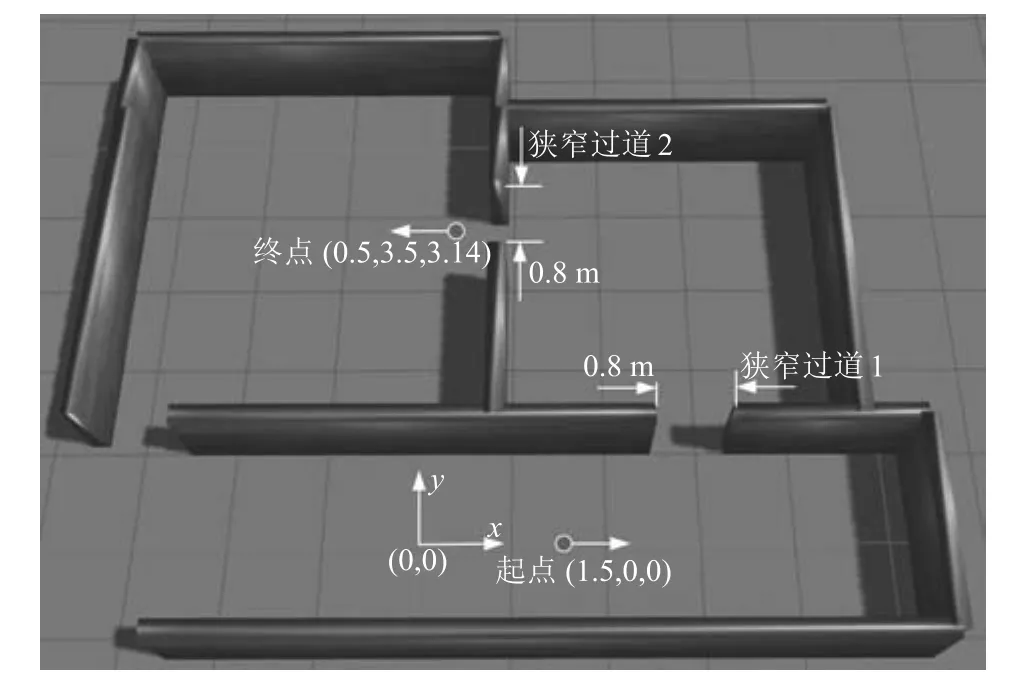
图7 算法比较的仿真环境Fig.7 Simulation environment for algorithm comparison

图8分别展示了由本文方法和A*算法产生的轮椅路径,由图8可以定性地看出A*算法产生的路径在2个狭窄通道处有“急转弯”,即有较大曲率,而本文提出的基于曲率优化方法产生的路径则没有“急转弯”,转弯过程较均匀的分配在整个路径中,而不会在通道处出现较大曲率,使路径较平滑.

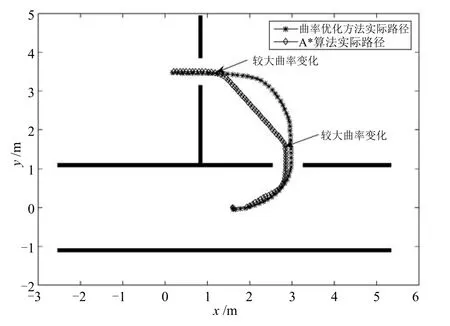
图8 基于本文方法和A*算法的轮椅路径Fig.8 Actual trajectories generated by the proposed method and A*algorithm

图9展示了两种方法产生的路径的曲率,可以看出,A*产生的路径的曲率具有多次跌宕起伏,最大曲率达到2.2,而基于曲率优化方法产生的路径的曲率只有2次起伏,且最大曲率仅为1.1,远小于A*产生的路径的曲率.因此,图9进一步说明了本文提出的基于曲率优化的算法可以实现比A*算法路径曲率更小且更加平滑的过狭窄通道过程.

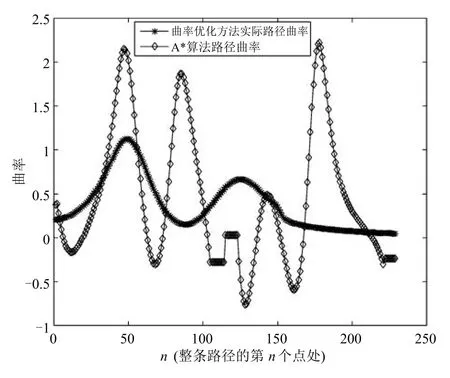
图9 基于本文方法和A*算法的路径曲率的比较Fig.9 The comparison of trajectory curvature generated by the proposed method and A*algorithm

另外,需要指出的是基于A*的路径规划导航算法需要事先构建好环境地图,然后再运行基于此地图的全局定位算法,而本文算法只需要根据传感器信息识别并计算狭窄过道相对于轮椅坐标系的相对坐标,而并不需要构建地图和全局定位,因此本文方法更简单且更易实现.

2.3 实时性分析

第2.2节仿真中基于内点法的优化方法计算复杂度较高,较大程度上影响了算法的实时性.为了评估本文算法的实时性,图10展示了算法每次循环中各模块运行时间及总时间.由图10可以看出,每次循环中基于内点法的路径规划模块所需运行时间在0.15s左右,而每次循环算法总时间约为0.2s,即5Hz,在轮椅线速度为0.15m/s时满足实时性要求.仿真运行的软硬件配置为:Intel i5 CPU,4GB RAM,操作系统为Linux 14.04,Matlab软件版本为R2015b.需要指出的是仿真算法是运行在解释性语言Matlab中,如果算法由编译性语言如C++等实现,算法运行时间将会更小,实时性可以更好.

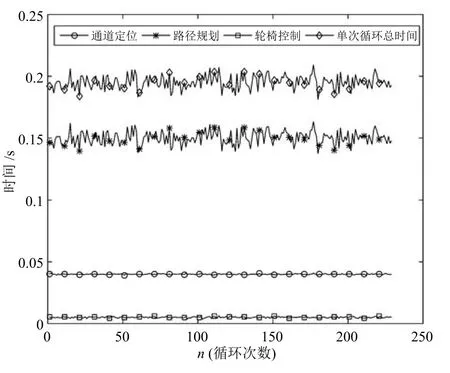
图10 算法每次循环中各模块运行时间及总时间Fig.10 Consuming time of each algorithm module and their total value for each iteration

3 实验

为了进一步验证和评估轮椅过狭窄通道的算法,用真实轮椅进行了实验.如图11(a)和图11(b)所示,轮椅的长度和宽度分别为85cm和65cm.采用激光测距仪测算通道位置.由于单个激光测距仪的视角不足以覆盖所有的安全区域,结合两个激光测距仪一起以构成更广视角.两个激光测距仪和后轮的距离为76cm,对应的偏向角θ1和θ2分别为46.36°和−56.50°.由于过道宽度为80cm,每一边留给轮椅的自由空间只有7.5cm.在实验之前,首先对两个激光测距仪之间的相对位置关系进行标定以使二者的数据具有一致性.

图11 轮椅和激光的配置Fig.11 Confguration of the wheelchair and the lasers

图12描述了实验场景(5m×5m),其中有一些墙壁和一间屋子.实线框住的是轮椅,其分别从A,B,C和D四个位置出发,穿过过道进入到屋子.轮椅的全局位置坐标由位置跟踪系统VICON获得,以评估算法的有效性.过通道算法的实现细节描述如下.

3.1 通道定位

利用来自两个激光测距仪的数据,通道定位算法计算通道中心位置及其对应的航向角Pd和Hd,其中航向角应垂直于过道平面,可由墙壁的斜率表示,即Hd=arctan(−1/Kw).Pd和Hd则作为产生贝塞尔曲线的输入参数.主要采用分割和直线拟合两个步骤计算Pd和Hd.

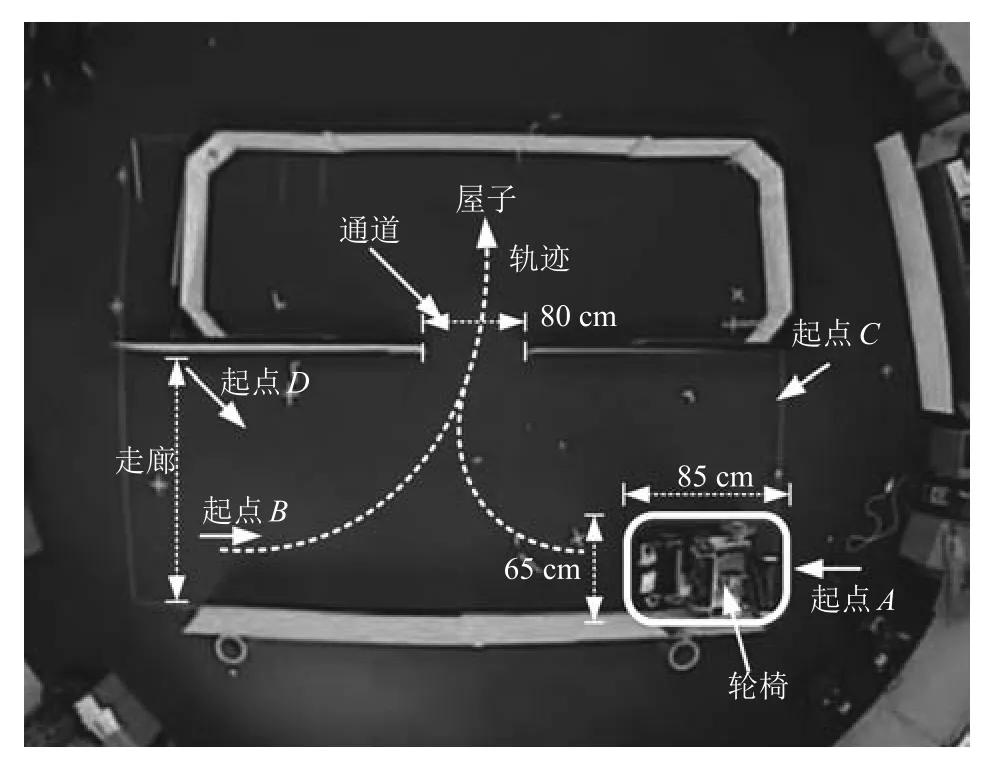
图12 实验场景Fig.12 Experimental scenario

3.1.1 分割

分割的目的在于将激光扫描数据分成几个不同的子集使得每个子集点属于一条直线.例如,如图12所示,一次完整的激光扫描数据点被分成6个子集.首先,采用算法Adaptive breakpoint detector (ABD)[26]通过检测断点来找到所有连续点集.如图13所示,共有三个点集:{1,2},{3}和{4,5,6}.然后,采用算法Iterative end-point ft(IEPF)[27]将每个连续点集分成不同的子集,以使每个子集的点都属于同一条直线.对每两个子集,计算第1个子集的末尾点(Pr)与第2个子集的起始点(Pf)之间的距离Drf,如果Drf等于过道的宽度,那么就找到了过道,并且Pd=(Pr+Pf)/2.如图9所示,通道在子集2和子集4之间找到了.

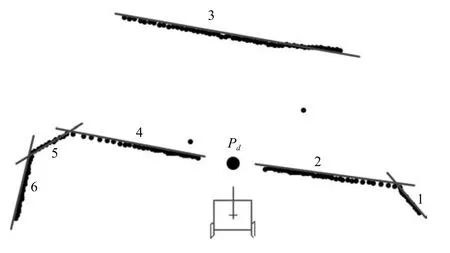
图13 一次激光扫描数据点及其分段Fig.13 A full scan of laser data points and its expected segmentations

3.1.2 直线拟合

在通道位置找到之后,接下来是要计算找到的通道所倚靠的墙壁的斜率Kw以确定Hd.Kw的计算可通过拟合对应于墙壁的所有激光数据点构成的直线来实现.直线拟合的目的是确定直线的参数.直线表示方法有多种,其中一个表示直线的参数形式为

其中,q和k分别为直线y的截距和斜率.假设有一个需要拟合的点集R={(xi,yi)|i=1,···,k},那么参数k和q可通过最小二乘直线拟合方法计算为

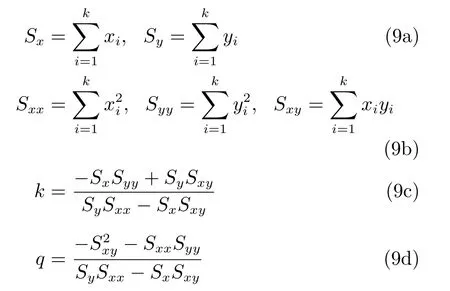
其中,式(9c)为直线斜率.

对于如图12所示的场景,激光点集2和点集4为构成墙壁的点.把这些点的笛卡尔坐标代入式(9a)～(9d)便计算出斜率Kw.

尽管路径规划算法已经设计好,但在实际中还不能直接用于轮椅,尤其是在轮椅大体积的情况下.下面就通过选择合适的起点P0和目标点P3,也就是Ps和Pd来解决这个问题.改进后的算法能产生在实际中令人满意的路径,且兼具光滑性和实用性.

3.2 控制点的选择

当新的贝塞尔曲线路径产生时,控制点P0的坐标总被设置为(0,0).然而,如图2所示,P0的位置可以是一般而言,应该选择因为有关过道的位置检测都是基于激光的位置.当轮椅作为一个质点或者激光和具有驱动力的轮子之间的距离很小时,选择是合理的.然而,由于轮椅的大体积,这两种情形都不适用于真实轮椅.而且,很难控制轮椅后轮使装在前面的激光跟踪规划好的路径.因此,在规划贝塞尔路径时,选为控制点如图2圆点所示.对应地,整个过通道算法策略都是基于坐标系{WC}.同时,选择比选择对于轮椅控制误差来说更具鲁棒性,因为对于相同的控制误差造成的偏差,的情形要多于因为Pcs距离Pls较远,在坐标系{WL}中计算出的通道的坐标需要平移至坐标系{WC}中.这个平移量只有沿X轴的量,且平移量为Pcs和Pls之间的距离,也就是如图2所示的L.

3.3 期望位置的选择

当轮椅到达过道中心时,激光位置可能恰好和墙壁共线,它们可能不能精确地检测到过道的位置甚至根本检测不到.同时由于现实情况下的各种干扰,轮椅的航向角不能恰好到达期望值.因此,轮椅需要在过通道时调整其航向角以使其垂直于过道平面,从而减小碰撞到过道框架的可能性.

为了克服这个问题,在确定Pd时,在过道定位环节中计算出来的值的基础上沿着Hd的方向设置一个偏移量,以保证激光有足够的前方距离来检测墙壁.于是,轮椅可以在位置而不是Pd调整其航向角垂直于过道平面,如图2所示.设偏移量为do,则新的Pd可表示为然而,由于贝塞尔曲线的控制点为偏移之后的点要被进一步偏移到才被当作控制点P3进而产生贝塞尔路径.可由下式计算出:

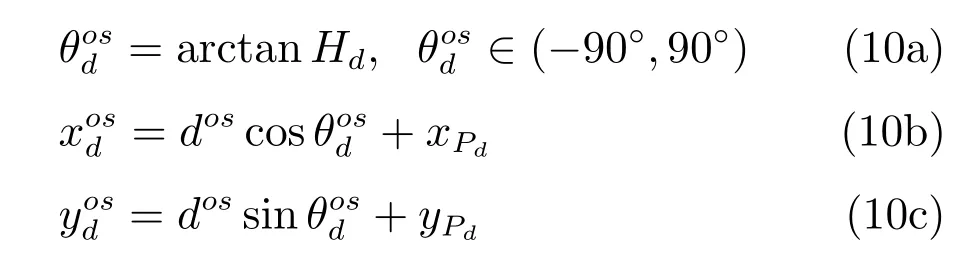
其中,(xPd,yPd)为通道位置Pd的坐标,为的坐标,dos为偏移量大小,包括实际偏移量do和轮椅的长度L.

从图14可以看出,由于轮椅尺寸大,单个激光测距仪不能检测整个通道的范围,这就可能造成计算出错误的路径和不合适的控制.而结合两个激光测距仪的方法可以为通道定位提供完整范围.

图14 两个激光测距仪相对于单个的优势Fig.14 Advantage of two lasers compared with single laser

图15展示了4个不同起点位置对应的轮椅的轨迹.对于每个起始位置,进行了2次试验.可以显然地看到,在每个起点,轮椅都能找到通道位置,然后平滑而精确地通过过道而不碰撞到通道两边边缘,证实了本文所提出算法的精确度和有效性.

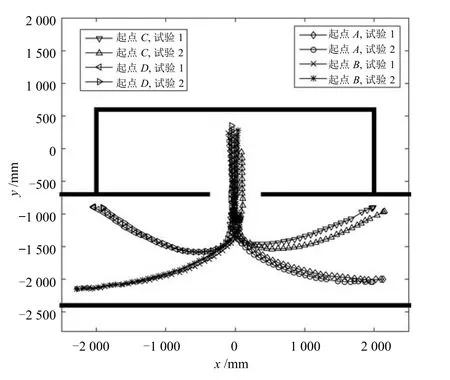
图15 轮椅轨迹Fig.15 Trajectories of the wheelchair

图16分别展示了轮椅在起点位置A,B,C和D对应的到达期望位置时的实际位置.可以看出,几乎所有的实际位置都在期望位置的附近,只略有较小误差,并且多数航向角都按期望的那样垂直于通道平面,尽管有些轻微地偏离了期望值.这些误差主要有两个原因:1)轮椅前面的随动轮在方向上造成较大干扰;2)选择Pd过程中的长偏移量放大了通道定位的误差.而实际位置和期望位置之间的水平误差都小于7.5cm,表明本文所提算法能减小来自现实的干扰和不确定性,从而使轮椅成功通过即使只有狭窄自由间隙的通道.这归功于根据轮椅位置连续不断地进行路径规划的策略.值得一提的是,如果不是采用这种策略,而采用只在第1次检测到通道时规划一条路径再控制轮椅跟踪这条路径的方法,会使轮椅不能到达期望位置,因为轮椅在跟踪此路径时需实时估计自身位置,而如果只依赖轮椅上的航位推算法而不借助其他定位算法,由于航位推算位置估算方法无限地累计误差会使跟踪误差越来越大,从而造成跟踪失败.

图17为每次试验在三个不同阶段的角速度变化曲线.在第一个阶段,角速度递增直到轮椅快要到达过道中间的位置;在第二个阶段,轮椅调整其航向角以保证航向角垂直于过道;在第三个阶段,轮椅径直走向屋子.需要指出的是在所有试验的第一个阶段,角速度平滑递增而没出现突变现象,再一次证明了算法成功实现了平滑过通道的目的.另外,对于同一个起始位置的两次不同试验,对应轮椅的角速度曲线重叠,表明算法的高可重复性.

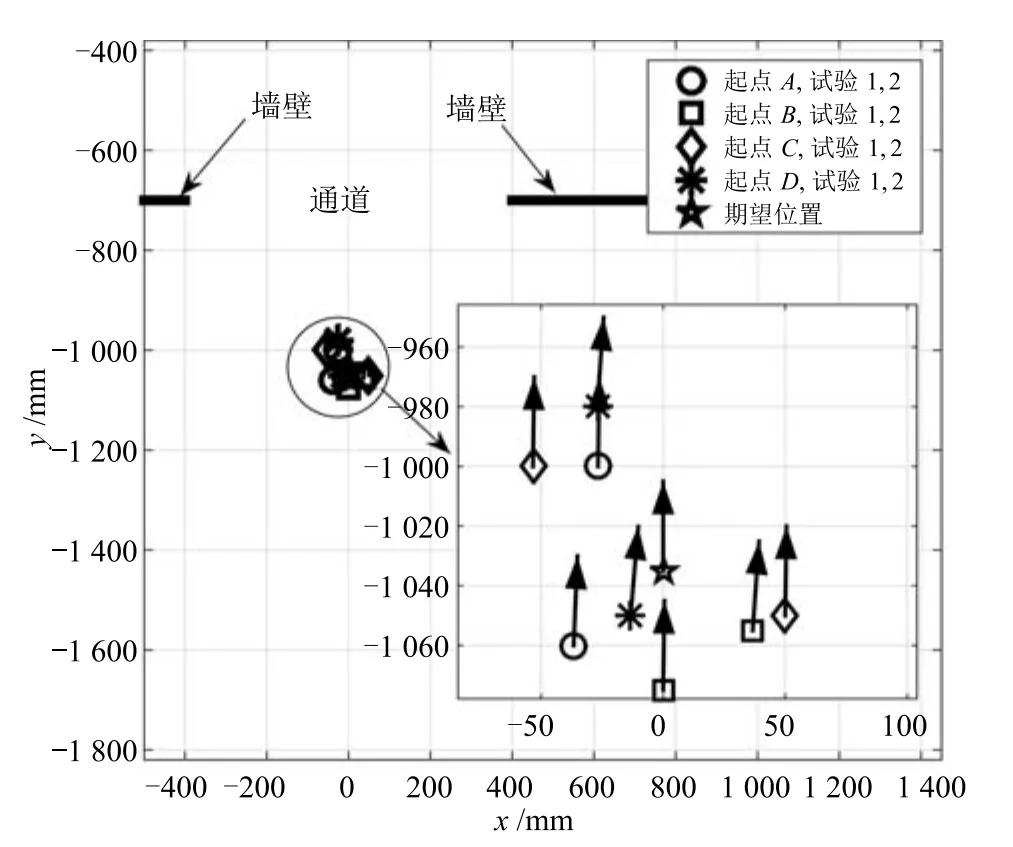
图16 轮椅从不同起点到达终点位置时的实际位置Fig.16 Actual wheelchair poses when arriving at the desired pose with diferent starting posesA,B,CandD

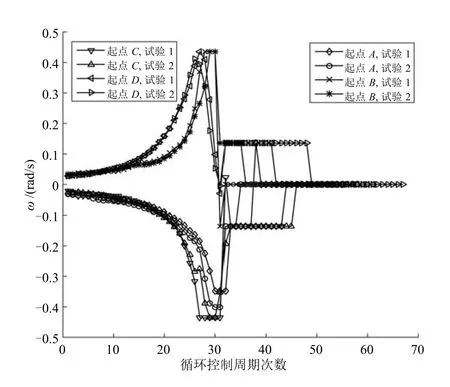
图17 轮椅的角速度Fig.17 Angular rate of the wheelchair

图18为轮椅从起点A和D出发的轨迹截图(因为相似性,起点B和C的截图在此省略),包括了几个重要的位置,如起点和在过通道前后的位置.在两个起点的第5张截图中,轮椅几乎在通道的中间位置,航向角也几乎垂直于通道平面,证实了算法的有效性.第6张截图也表明轮椅能以期望的航向角穿过通道.

图18 轮椅从起点A和D出发过通道轨迹截图((a)～(f)对应于起点A,(g)～(l)对应于起点D)Fig.18 Snapshots of the wheelchair's trajectories when passing gap,starting from poseAandD((a)～(f), (g)～(l)are with poseAandD,respectively.)

4 结论

本文提出了一种智能轮椅通过狭窄通道的新颖方法.狭窄通道指自由空间只有几厘米的门或者过道.所提出的路径规划算法基于贝塞尔曲线曲率优化,从而产生平滑的路径以控制轮椅跟踪此路径.算法按照“定位通道”→ “产生贝塞尔曲线路径”→“跟踪产生的路径”的顺序连续执行.算法考虑轮椅和环境的各种约束,能够在没有全局坐标或者里程计的情况下平滑地穿过狭窄通道.

首先,进行了仿真来验证算法的核心部分,即基于贝塞尔曲线的曲率优化的路径规划算法.然后仿真比较了本文算法与基于A*的路径规划开源导航算法在路径平滑度上的表现,分析了算法实时性.最后用装有两个激光测距仪的真实轮椅进行对算法的实验验证,结果证实了整个算法的可行性和有效性.算法不仅适用于轮椅,还可用于其他各类想要通过狭窄通道的移动机器人.未来的工作主要测试轮椅在不同复杂室内环境下的过通道算法,比如办公室、购物中心、居家和医院等,主要解决过不规则障碍物的问题.

1 Elbanhawi M,Simic M,Jazar R N.Continuous path smoothing for car-like robots using B-spline curves.Journal of Intelligent and Robotic Systems,2015,80(1):23−56

2 Yoon S,Yoon S E,Lee U,Shim D H.Recursive path planning using reduced states for car-like vehicles on grid maps.IEEE Transactions on Intelligent Transportation Systems, 2015,16(5):2797−2813

3 Pan Z,Li J Q,Hu K M,Zhu H.Intelligent vehicle path planning based on improved artifcial potential feld method.Applied Mechanics and Materials,2014,742:349−354

4 Zhang Hao-Jie,Gong Jian-Wei,Jiang Yan,Xiong Guang-Ming,Chen Hui-Yan.Research on incremental heuristic path planner with variable dimensional state space.Acta Automatica Sinica,2013,39(10):1602−1610 (张浩杰,龚建伟,姜岩,熊光明,陈慧岩.基于变维度状态空间的增量启发式路径规划方法研究.自动化学报,2013,39(10):1602−1610)

5 Zu Di,Han Jian-Da,Tan Da-Long.LP-based path planning method in acceleration space for mobile robot.Acta Automatica Sinica,2007,33(10):1036−1042 (祖迪,韩建达,谈大龙.加速度空间中基于线性规划的移动机器人路径规划方法.自动化学报,2007,33(10):1036−1042)

6 Park J W,Im W S,Kim D Y,Kim J M.Safe driving algorithm of the electric wheelchair with model following control.In:Proceedings of the 16th European Conference on Power Electronics and Applications.Lappeenranta,Finland: IEEE,2014.1−10

7 Sinyukov D A,Padir T.Adaptive motion control for a differentially driven semi-autonomous wheelchair platform.In: Proceedings of the 2015 International Conference on Advanced Robotics.Istanbul,Turkey:IEEE,2015.288−294

8 Zhang Z Y,Zhao Z P.A multiple mobile robots path planning algorithm based on a-star and Dijkstra algorithm.International Journal of Smart Home,2014,8(3):75−86

9 Bhadoria A,Singh R K.Optimized angular a star algorithm for global path search based on neighbor node evaluation.International Journal of Intelligent Systems and Applications, 2014,6(8):46−52

10 Seder M,Mostarac P,PetroviI.Hierarchical path planning of mobile robots in complex indoor environments.Transactions of the Institute of Measurement and Control,2011,33(3−4):332−358

11 BSI.Design of Buildings and Their Approaches to Meet the Needs of Disabled People.Code of Practice.Standard Number BS 8300:2009+A1:2010,ISBN 978 0 580 70730 8，British Standards Institute,2009.

12 Cheein F,De La Cruz C,Guimaraes E,Bastos-Filho T, Carelli R.Navigation system for UFES's robotic wheelchair.Devices for Mobility and Manipulation for People with Reduced Abilities.Boca Raton,FL:CRC Press,2014.41−93

13 Peula J M,Urdiales C,Herrero I,Fernandez-Carmona M, Sandoval F.Case-based reasoning emulation of persons for wheelchair navigation.Artifcial Intelligence in Medicine, 2012,56(2):109−121

14 Rastelli J R,Lattarulo R,Nashashibi F.Dynamic trajectory generation using continuous-curvature algorithms for door to door assistance vehicles.In:Proceedings of the 2014 IEEE Intelligent Vehicles Symposium.Dearborn,USA: IEEE,2014.510−515

16 Chu C H,Hsieh H T,Lee C H,Yan C Y.Spline-constrained tool-path planning in fve-axis fank machining of ruled surfaces.The International Journal of Advanced Manufacturing Technology,2015,80(9−12):2097−2104

17 Simba K R,Uchiyama N,Sano S.Real-time smooth trajectory generation for nonholonomic mobile robots using Bzier curves.Robotics and Computer-Integrated Manufacturing, 2016,41(1):31−42

18 Yang L,Song D L,Xiao J Z,Han J D,Yang L Y,Cao Y.Generation of dynamically feasible and collision free trajectory by applying six-order Bezier curve and local optimal reshaping.In:Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS).Hamburg,Germany:IEEE,2015.643−648

20 Chen Cheng,He Yu-Qing,Bu Chun-Guang,Han Jian-Da.Feasible trajectory generation for autonomous vehicles based on quartic Bzier curve.Acta Automatica Sinica, 2015,41(3):486−496 (陈成,何玉庆,卜春光,韩建达.基于四阶贝塞尔曲线的无人车可行轨迹规划.自动化学报,2015,41(3):486−496)

21 Choi J W,Curry R,Elkaim G.Piecewise Bezier curves path planning with continuous curvature constraint for autonomous driving.Machine Learning and Systems Engineering.Netherlands:Springer,2010.31−45

22 Hart P E,Nilsson N J,Raphael B.A formal basis for the heuristic determination of minimum cost paths.IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100−107

23 Open Source Robotics Foundation(OSRF).Robot operating system[Online],available:http://www.ros.org,May 21, 2016

24 Open Source Robotics Foundation(OSRF).Gazebo[Online],available:http://www.gazebosim.org/,May 21,2016

25 Open Source Robotics Foundation(OSRF).Global planner of navigation stack in ROS[Online],available:http://wiki. ros.org/global_planner?distro=indigo,May 21,2016

26 Borges G A,Aldon M J.Line extraction in 2D range images for mobile robotics.Journal of Intelligent and Robotic Systems,2004,40(3):267−297

27 Duda R O,Hart P E.Pattern Classifcation and Scene Analysis.New York:Wiley,1973.

陈 灵上海大学机电工程与自动化学院助理研究员.主要研究方向为机器人定位与导航.本文通信作者.

E-mail:lcheno@shu.edu.cn

(CHEN LingAssistant professor at the School of Mechatronics Engineering and Automation,Shanghai University. His research interest covers localization and navigation of robots.Corresponding author of this paper.)

王 森英国牛津大学计算机科学学院助理研究员.主要研究方向为机器人定位和多传感器融合.

E-mail:sen.wang@cs.ox.ac.uk

(WANG SenAssistant professor in the Department of Computer Science, University of Oxford,Oxford,UK.His research interest covers robot localization and multiple sensor fusion.)

胡豁生英国埃塞克斯大学计算机科学与电子系统学院教授,机器人实验室主任.主要研究方向为自主机器人和网络化机器人.E-mail:hhu@essex.ac.uk

(HU Huo-ShengProfessor at the School of Computer Science and Electronic Engineering,University of Essex, UK,leading robotics research.His research interest covers autonomous robots and networked robots.)

麦当劳-麦尔·克劳斯英国埃塞克斯大学计算机科学与电子系统学院教授.主要研究方向为嵌入式系统和机器人应用.E-mail:kdm@essex.ac.uk

(MCDONALD-MAIER KlausProfessor at the School of Computer Scienceand ElectronicEngineering, University of Essex,UK.His research interest covers embedded systems and application of robotics.)

费敏锐上海大学机电工程与自动化学院教授.主要研究方向为网络化控制系统,智能机器人系统.

E-mail:mrfei@staf.shu.edu.cn

(FEIMin-RuiProfessor at the SchoolofMechatronicsEngineering and Automation,Shanghai University. His research interest covers networked control system and intelligent robot system.)

Novel Path Curvature Optimization Algorithm for Intelligent Wheelchair to Smoothly Pass a Narrow Space

CHEN Ling1WANG Sen2HU Huo-Sheng3MCDONALD-MAIER Klaus3FEI Min-Rui1

This paper presents a novel algorithm to address the smooth narrow pass traversing issue,which is based on optimizing the curvature of the wheelchair path.Being aware of the fact that the path smoothness is determined by the path curvature and its change rate,after calculating the position of the narrow pass relative to the base frame of the wheelchair from perception sensor data,the algorithm takes the curvature and its change rate of Bezier curve as the optimal objective,and the wheelchair heading and the condition that the Bezier curve polygon should be convex polygon as constraints,and plans a smooth and optimal path for the controlled wheelchair to follow.This process is iterated dynamically to enable the intelligent wheelchair to traverse the narrow pass smoothly.Simulation is frstly conducted to compare the performances of our method and the A*-based path planning navigation algorithm,which shows that the proposed algorithm is able to achieve more smooth path with smaller curvature when the wheelchair traverses narrow path.Furthermore,the algorithm can control the wheelchair to traverse narrow pass smoothly even without any global map and localization.Real experiment with detailed explanation of algorithm implementation is also given to verify the efectiveness of the proposed algorithm.

Intelligent wheelchair,curvature optimization,Bezier curve,pass traversing

陈灵,王森,胡豁生,麦当劳-麦尔·克劳斯,费敏锐.保证智能轮椅平滑通过狭窄通道的路径曲率优化算法.自动化学报,2016,42(12):1874−1885

Chen Ling,Wang Sen,Hu Huo-Sheng,Mcdonald-Maier Klaus,Fei Min-Rui.Novel path curvature optimization algorithm for intelligent wheelchair to smoothly pass a narrow space.Acta Automatica Sinica,2016,42(12):1874−1885

2016-03-01 录用日期2016-07-11

Manuscript received March 1,2016;accepted July 11,2016

上海市科委扬帆人才计划项目(16YF1403700),上海市科委重点项目(15411953502,14JC1402200),上海高校青年教师培养资助计划(ZZ SD15088)资助

Supported by Shanghai Sailing Program(16YF1403700),Key Project of Science and Technology Commission of Shanghai Municipality(15411953502,14JC1402200),and Shanghai Colleges and Universities Young Teachers Training Funding Scheme(ZZS D15088)

本文责任编委程龙

Recommended by Associate Editor CHENG Long

1.上海大学机电工程与自动化学院上海200072中国 2.牛津大学计算机与电子工程学院牛津OX1 3QD英国 3.艾塞克斯大学计算机与电子工程学院科尔彻斯特CO4 3SQ英国

1.School of Mechatronics Engineering and Automation,Shanghai University,Shanghai 200072,China 2.Department of Computer Science,University of Oxford,Oxford OX1 3QD,UK 3.School of Computer Science and Electronic Engineering,University of Essex,Colchester CO4 3SQ,UK