一种基于非线性振荡器的步态轨迹自适应算法

罗林聪 侯增广 王卫群 彭亮

一种基于非线性振荡器的步态轨迹自适应算法

罗林聪1,2侯增广1,3王卫群1彭亮1

步态训练轨迹是影响康复训练效果的一项重要因素,而自适应性对于下肢康复机器人的临床应用具有重要的意义.振荡器可通过在线调节参数而输出不同波形的周期信号,常用于康复机器人步态轨迹的生成.本文在高斯核函数非线性振荡器的基础上提出了一种下肢康复机器人步态轨迹自适应算法.该算法通过轨迹偏差实现对参考轨迹波形的调节,并且用相位偏差曲线面积实现参考轨迹周期的自适应.本文首先介绍了用于生成步态参考轨迹的非线性振荡器的数学模型;其次,详细描述了基于该模型的参考轨迹波形和周期自适应算法;最后,以悬挂减重式下肢康复机器人为研究对象,建立机器人与人体下肢仿真模型,对所提出的步态参考轨迹自适应算法进行仿真实验,并验证了该算法的可行性.

下肢康复机器人,步态轨迹,振荡器,自适应算法,步态训练

DOI10.16383/j.aas.2016.c160205

脊髓损伤和中风使患者丧失了部分肢体运动功能,严重影响了患者的日常生活[1].为了恢复或改善下肢运动功能,患者需要做大量的步态康复训练[2].传统的步态训练方法,通常需要在多个理疗师的辅助下才能完成.由于体力限制,理疗师不能长时间辅助患者进行康复训练,加上传统训练方法精度低、可重复性差使得康复训练效果并不理想[3].

为了弥补传统康复训练方法的不足,机器人和自动化技术被引入到康复领域[4−7].采用康复机器人辅助或代替理疗师为患者做步态康复训练,可以使理疗师从高密度的体力劳动中解放出来,从而把更多的时间放在康复训练的指导和决策上.根据步态轨迹的不同驱动机理[8],可把下肢步态训练康复机器人分为外骨骼式和末端牵引式.外骨骼式康复机器人是通过外骨骼机械臂带动人体下肢做步态训练.图1是由瑞士Hocoma公司商业化的Lokomat下肢外骨骼康复机器人,其具有4个自由度,能实现对髋膝关节的康复训练[9].与Lokomat相比,ALEX和PAM/POGO添加了对骨盆关节的康复训练,前者的第三代样机已经发展为具有12自由度的外骨骼康复机器人[10−11],后者是由骨盆驱动机构和下肢外骨骼两部分组成的6自由度康复机器人[12].为了增加关节柔顺性,LOPES利用具有柔顺特性的弹性驱动器实现对各关节的驱动[8].末端牵引式康复机器人通过踏板带动患者的脚部按一定轨迹做步态训练,如GT I[13]和HapticWalker[14].与外骨骼式康复机器人相比,这类康复机器人可以更加灵活地模拟出人体各种步态轨迹,但难以实现对髋膝关节准确的力矩/位置控制,目前多数科研人员还是选择外骨骼式的下肢康复机器人作为研究对象.

无论哪种下肢康复机器人,在给患者进行步态训练时都要面临参考轨迹的规划问题.步态参考轨迹的规划在一定程度上会影响患者的康复效果.一般可通过采集健康人的步态轨迹或者记录理疗师辅助患者做步态训练时的轨迹作为康复机器人的参考轨迹[15−17].但该方法所得到的参考轨迹比较单一,难以调动患者参与步态康复训练的积极性,影响康复效果.此外,也容易因患者与康复机器人的步态相位不同步造成患者肌肉损伤.

图1 Lokomat康复机器人[18]Fig.1 Lokomat rehabilitation robot[18]

为了解决参考轨迹单一的问题,科研人员给出了不同的解决方案.Vallery等提出一种CLME (Complementary climb motion estimation)方法,该方法根据健侧的运动轨迹生成患侧的参考轨迹[19].Banala等在康复训练系统中设定了一系列参考轨迹模板,根据患者在康复训练中的状态调用不同的参考轨迹模板[10].为了使步态康复训练过程中的参考轨迹与人的步态轨迹同步,科研人员提出了参考轨迹自适应的方法.Riener等先建立参考轨迹的参数模型,分别从人机系统的直接动力学和逆动力学出发,利用求取的人机交互力矩去优化目标函数,从而实现轨迹参数的自适应[20].此方法可以做到对参考轨迹波形和周期的调整,但函数优化的复杂计算会对临床运用中康复机器人的实时控制造成影响.Aoyagi等把参考轨迹以时间序列的形式存储在列表中,基于最短距离原理,利用机器人的执行轨迹与参考轨迹的相位偏差去修正参考轨迹时间序列的输出速率[12].该方法虽然比较简单,但只能根据患者的不同步态速率调整参考轨迹的周期,而不能修改轨迹的波形,导致参考轨迹过于单一.CPG (Central pattern generator)常常被运用于仿生类机器人周期性的运动控制[21].因为人体步态是一种节律性动作,有科研人员把振荡器运用于康复机器人轨迹的预测和自适应设计.Zanotto等结合频率自适应振荡器和非线性滤波器,通过学习患者的健侧步态轨迹,生成患侧的参考轨迹[11].其中对步态轨迹频率的学习是该方法的重点.Seo等利用自适应频率振荡器估计人体步态的频率,实现了外骨骼机器人与患者步态的同步[22].Ronsse等利用振荡器实现了单关节单一正弦波运动轨迹频率的学习[23],但是,如果要估计的周期信号是非正弦的周期信号时,需通过并联多个振荡器去估计每个频率分量,然后利用逻辑算法判断出基频(步态周期所对应的频率).该方法存在某些不足,频率初始化不合适时会出现频率重叠甚至负频率的现象,另外振荡器的收敛值还受频率分量的幅值影响[24−25].

本文将一种基于高斯核函数的非线性振荡器作为步态参考轨迹生成的参数化模型,针对步态康复训练中参考轨迹的波形与周期的自适应问题,分别提出了相应的解决方法.本文利用参考轨迹与康复机器人实际轨迹的关节角度、角速度和角加速度的偏差去调节非线性振荡器参数,从而实现参考轨迹波形的自适应.此方法与上述利用交互力矩去优化参考轨迹的方法相比,无需测量人机交互力,并且省去复杂的参数优化过程.而与存储轨迹时间序列的自适应方法相比,本方法增加了参考轨迹波形的多样性.另外,为了实现参考轨迹周期的自适应,本文提出了一种相位偏差曲线面积法,利用相位的偏差修正参考轨迹的周期.与用频率自适应振荡器估计非正弦周期信号的基频方法相比,该方法无需对周期信号中的每个频率进行估计,而且可以避免出现负频率,能有效地实现对参考轨迹周期的调整.

本文的结构安排如下:第1节主要介绍用于生成参考轨迹的非线性振荡器的数学模型;第2节给出参考轨迹波形与周期的自适应算法;第3节进行系统仿真实验,并对实验结果进行分析和讨论;第4节对全文进行总结.

1 步态轨迹的参数化模型

为了防止混淆,本文中的步态轨迹是指关节角度.在步态康复训练中参考轨迹的生成可以利用某种数学模型来完成.该模型应相对简单且参数可调.参考轨迹的数学建模方法主要有如下几种方法:

1)以采集的步态轨迹数据作为参考轨迹的输出时间序列[12].该方法简单直接,可根据步态周期来调整输出的时间序列.但是,为了能反映出步态轨迹的更多细节信息,需要较大的存储空间.另外,该方法无法通过简单的参数调整来改变输出轨迹的波形.

2)存储关键的数据点,通过插值方法算出轨迹的其他数据点.该方法解决了方法1)存储空间不足的问题,但此方法存在输出曲线不平滑的问题.

3)考虑到人体步态轨迹的周期性,可以用多阶傅里叶级数去拟合步态轨迹[26].通过改变频率参数去适应不同周期下的步态轨迹.然而,当需要重新调整步态轨迹波形时,需要经过较为复杂的拟合和优化的过程去求取傅里叶级数的参数,该计算过程将对临床运用中康复机器人的实时控制造成影响.

因为人体的步态轨迹是一种节律性信号,所以本文选用一种基于核函数的非线性振荡器来实现对参考轨迹的建模,并运用于参考轨迹的自适应算法.利用步态轨迹采样点的角度、角速度和角加速信息确定模型中的待定参数,然后在生成参考轨迹时,通过调节非线性振荡器的参数来改变参考轨迹的上下偏移量、幅值和周期.非线性振荡器的数学模型如下式:

其中,Ω是周期信号的角频率,φ是相位;y和z是状态变量,其中y在本文作为参考轨迹所对应的关节角度;g是系统状态y的吸引子,y围绕其上下变化,本文取g=0;α、β是正的常系数,取α=4、β=1, 4:1的比值是为了确保系统能在临界阻尼状态下围绕吸引子单调变化;ψi是关于相位φ的类高斯核函数;N是类高斯核函数ψi的个数,本文取N=100;ωi是核函数的权重系数,该系数的分布决定轨迹的形状;r是正系数,它决定轨迹的幅值,本文取r=1;h是正的系数,决定核函数的宽窄,本文取h=2.5N;ci是在0～2π区间上等间隔分布的数值;关于该模型的详细介绍可参考文献[24].

在Ω一定的情况下,由上面的非线性动态系统产生的轨迹y将绕g做周期性变化.轨迹的波形由权值ωi的分布决定.换句话说,只要求得模型中的权值ωi就能确定参考轨迹的波形,并且可以通过修改Ω、g、r来调整轨迹的频率,上下偏移量和幅值.

为了实现参考轨迹向期望轨迹的调整,首先需要设定一个初始参考轨迹.初始参考轨迹的生成可以参考本文前面所提到的参考轨迹生成方法(选用网上的步态数据、采集健康人的步态轨迹、采集在理疗师辅助下的步态轨迹).在获取步态轨迹数据后,为了能用上述非线性振荡器模型复现所对应的参考轨迹曲线,我们需要求出参考轨迹所对应的权值ωi.

在文献[24]中Gams等用带遗忘因子的加权最小二乘递归算法求取权重系数ωi,而当h=2.5N时,下式成立

其中,i将根据参数φ的变化而在1～N区间上取不同的整数.

因此,可以根据采样点的角度、角速度和角加速度,直接求得权重系数ωi,省去繁琐的寻优过程,减小了运算量,提高了参考轨迹自适应算法的实时执行效率.

2 参考轨迹的自适应算法

假设患者在下肢康复机器人上做步态训练时,自身会有一个期望步态轨迹.在康复机器人按设定的参考轨迹运动过程中,当人的期望步态轨迹和康复机器人的参考轨迹不一致时,人体和康复机器人之间会产生作用力,该作用力使康复机器人偏离参考轨迹而趋向人的期望步态轨迹,使康复机器人的实际轨迹和参考轨迹之间形成误差.当患者的期望轨迹与康复机器人的参考轨迹相差越大时,则产生的这种误差越大.在理想情况下,初始的参考轨迹和患者的期望步态轨迹一致时,人体和康复机器人之间不会有作用力,那么康复机器人将完全按照设定的参考轨迹运动.综上,利用康复机器人的实际轨迹与参考轨迹的误差曲线可以调整参考轨迹趋近人的期望轨迹.下面将分别介绍参考轨迹的波形自适应算法和周期自适应算法.

2.1 参考轨迹波形的自适应算法

考虑参考轨迹的周期与患者的期望步态轨迹周期相同的情况下,只对参考轨迹的波形进行调整.即固定上述非线性振荡器数学模型中决定信号周期的参数Ω,只对模型中的权重系数ωi进行调整.算法的执行周期为一个步态周期,即当康复机器人执行完一个完整的步态轨迹时,自适应算法调整下一个周期的参考轨迹.具体的算法如下:

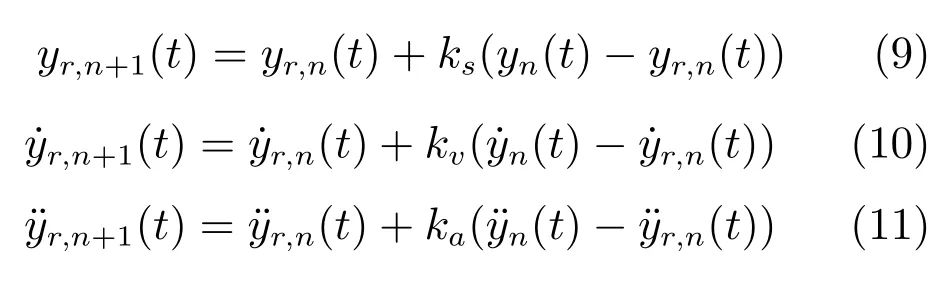
2.2 参考轨迹周期的自适应算法

周期信号频率的自适应可以采用自适应频率振荡器实现.Ronsse等利用Hopf振荡器成功跟随单一频率的正弦波信号[23].对于非正弦的周期信号,信号中的每个频率分量都是一个吸引子会对振荡器产生吸引作用.导致振荡器频率的收敛值会受振荡器的初始设定频率以及输入信号中各频率分量的幅值影响[25],只有当周期信号中基频信号幅值远大于其他频率幅值时,才能使振荡器频率收敛到基频值.为了解决这个问题Petric等提出并联多个振荡器去估计周期信号中的不同频率成分[24,27],只有当各个振荡器的初始化频率合适时,此方法才能使振荡器的频率分别收敛到周期信号的不同频率值,但在初始频率不恰当时,会出现频率重叠甚至负频率的现象.

考虑到人体步态轨迹的频率不会出现突变或激烈变化,本文提出了一种利用自定义的轨迹相位偏差曲线面积去修正参考轨迹周期的方法.本文在利用上述参考轨迹波形自适应的算法去跟随人体期望步态轨迹时,当人体期望步态轨迹的周期比机器人的参考轨迹的周期要大(小)时,如图2所示机器人的实际执行轨迹要比参考轨迹滞后(超前).这种超前或滞后是两周期信号相位偏差的反映.而相位的偏差,可以认为是周期信号角频率(周期)的不一致,造成相位偏差的累积.于是本文提出了如下参考轨迹周期的修正方法:

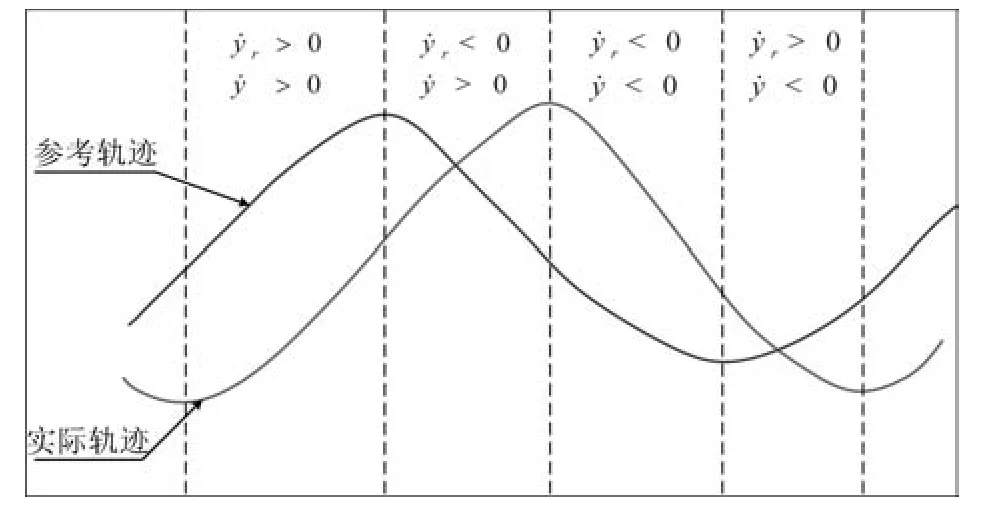
图2 相位偏差Fig.2 Phase deviation

其中,yr(t)、y(t)分别是参考轨迹和实际轨迹;∆s(t)是一种自定义的偏差曲线,它能反映两周期信号之间相位的偏差.当两轨迹所对应的角速度同向时,∆s(t)等于两者的差值,当速度方向相反时,∆s(t)计为零;∆Tint是轨迹偏差的积分时间;Sn+1是在∆Tint内对∆s(t)积分的平均值,一定程度上反映两个周期信号之间的周期差值;对于积分时间∆Tint较小的取值能加快算法的自适应速度,但过小的积分时间容易引起步态周期的振荡不利于算法的稳定;Ωn、Ωn+1是调整前后的非线性振荡器角频率参数;参数Kp、Ki是参考轨迹周期自适应算法的调节参数,等式(14)右边的第2项起到减小超调量的作用;Tn+1是更新后的参考轨迹周期值.

3 实验仿真与结果分析

为验证上述参考轨迹自适应算法在康复机器人步态训练中的可行性.本文以外骨骼式带悬挂减重系统的康复机器人作为研究对象.上述提出的步态自适应方法并不局限于该类平台,也可以运用于其他形式的下肢康复机器人的步态训练.

3.1 仿真模型的建立

当人体在外骨骼式带悬挂减重系统的康复机器人上做步态运动时,假定通过减重系统把人体上身的重力抵消,而人体下肢则依附在康复机器人的机械腿上,患者在机器人的带动下做步态训练.假定人的踝关节固定在康复机器人的踝关节处,人腿和机械腿之间不产生相对运动.本文把康复机器人的机械腿和人腿看作质量均匀分布的两连杆结构.考虑到人体步态的对称性,只研究一侧的下肢关节运动.图3是整个系统的结构示意图.

图3 系统结构图Fig.3 System block diagram

利用拉格朗日-欧拉方程建立两连杆的人机系统动力学方程[9]:

为了实现参考轨迹的自适应,人体必须提供一定的主动力矩去影响机械臂的运动轨迹,因此要建立从人体期望步态轨迹到主动力矩的模型.文献[9]利用虚拟弹簧去模拟人腿和康复机器人之间的作用力矩.根据前文的假设,当人体的期望步态轨迹和机械腿的实际轨迹不一致时,将会产生主动力矩影响机器人轨迹.另外根据人体的阻抗特性,本文假设人腿是一个虚拟的阻尼弹簧,可根据当前康复机器人的步态轨迹和人的期望轨迹的角度、角速度偏差产生一定的输出力矩.这个假设符合我们的直观感受:在步态训练中当机器人关节角度与人体期望的角度不一致时,人体会设法改变当前的关节角度;另外关节角速度太快而跟不上时,人体将会产生一个阻碍机器人运动的力矩.于是可用下式表示人体的主动力矩:

其中,Kh、Bh分表是弹簧系数和阻尼系数;∆qh、∆h分别是关节空间中人体期望的步态轨迹与康复机器人实际步态轨迹的角度偏差和角速度偏差;

阻抗控制[28]是康复机器人领域常用的一种控制算法.因为它能在康复机器人和患者之间产生柔顺的交互作用,能够激发患者的主动运动.在没有外力或干扰作用下,机器人稳定在期望的位置和速度.当有外力作用时,它允许机器人的末端位置和参考轨迹有一定的偏差.阻抗控制的这种特性允许人体主动力矩影响机器人轨迹,从而实现步态轨迹自适应的目的.因为康复训练过程中角加速度很小,可以简化阻抗控制方程:

此外,加上科氏力和重力的补偿项可得机器人的输出力矩如下式:

其中,τi是阻抗控制输出项;τr是机器人的输出力矩;Kr、Br分别是康复机器人的刚度系数和阻尼系数;TC、TG分别是科氏力和重力补偿项;∆qr、∆r分别是参考轨迹与机器人实际轨迹的角度偏差和角速度偏差.

3.2 实验结果与分析

本节以上文建立的仿真模型为基础,在Matlab/Simulink环境下对所提出的参考轨迹自适应算法进行仿真.为了模拟真实的人体步态轨迹,本文利用参考文献[26]中的四阶傅立叶级数生成人体期望轨迹yd.为了充分验证参考轨迹波形自适应和周期自适应算法的有效性,分别在以下三种不同的初始条件下,考察自适应算法的效果.

1)假定期望轨迹的周期已知,初始参考轨迹和期望轨迹的周期相同但波形不同;

2)假定期望轨迹的波形已知,初始参考轨迹和期望轨迹的波形相同但周期不同;

3)假定期望轨迹的波形和周期都未知,初始参考轨迹与期望轨迹的波形和周期都不同.

采用初始化条件1)时,设定期望轨迹的周期Td=2s,并且把参考轨迹的周期也固定为2s.在式(9)～(11)中,髋关节所对应的调节参数ks,kv,ka取值都为0.65,膝关节所对应的参数取值都为0.5.

参考轨迹波形自适应算法的结果如图4所示.图4(a)中的实线是参考轨迹,点画线是机器人实际轨迹,虚线是人的期望轨迹.可以看到参考轨迹一直处在机器人的实际轨迹和人体期望步态轨迹之间.大致经过三个步态周期后,髋关节的参考轨迹和期望的髋关节轨迹基本一致,膝关节的参考轨迹大致经过三个步态周期后跟踪上期望轨迹.因为不同患者不同条件下不同关节角度的范围有所差异,为了统一定量刻画髋膝关节参考轨迹的自适应效果,本文以一个步态周期内参考轨迹yr和期望轨迹yd的相对均方根误差(Relative root mean square error, RRMSE)作为评价指标,具体表达式如下:

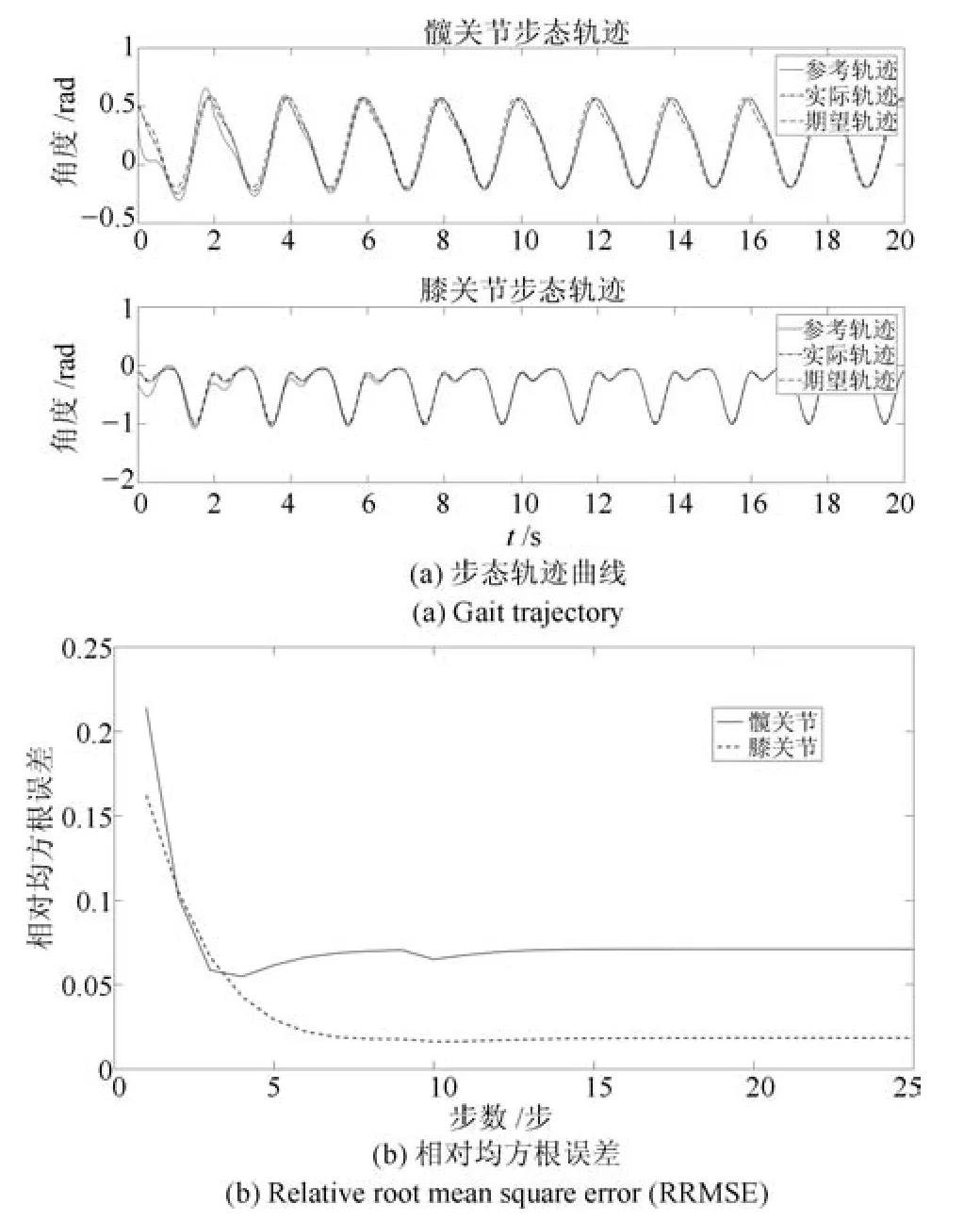
图4 条件1)下的波形自适应结果Fig.4 The waveform adaptation results on condition 1)

其中,yd,max、yd,min分别是期望轨迹的最大值和最小值.如图4(b)所示,髋关节相对均方根误差由0.22降到了0.06,并在第5个步态周期稳定下来;膝关节由0.17降到了0.02,并在第6个步态周期稳定下来.

采用初始条件2)时,初始参考轨迹的波形与期望轨迹一样,期望步态轨迹的周期Td=2s,初始参考轨迹的周期Tr=1.5s.式(13)中相位偏差曲线积分时间取值为1/32个步态周期,式(14)中参数Kp、Ki的取值分别是2.5、1.1.根据人体步态的特征,髋关节和膝关节的步态轨迹周期可不作区分.另外补充一点,尽管该条件下的实验是为了验证周期自适应的算法,但波形调节算法也需要同时执行,否则会因为参考轨迹和期望步态轨迹波形的长时间不一致,而导致康复机器人实际输出轨迹的混乱.初始条件2)下的实验结果如图5所示.

图5(a)中的上图是式(12)中定义的∆s变化曲线,而图5(a)中的下图是参考轨迹周期的变化曲线.从图5(a)可以看出参考轨迹和实际轨迹持续着正的相位偏差,说明参考轨迹超前于期望步态轨迹.从周期的调节曲线可以看出,在第5个步态周期时,参考轨迹的周期已经达到目标值并有所超调,在15s后稳定于目标值.周期超调是因为在跟踪上目标值之前参考轨迹的周期一直小于目标值,导致相位有所超前于目标轨迹.为了补偿相位的偏差,参考轨迹的周期值有所超调.

采用初始条件3)时,期望轨迹周期Td=2s,初始参考轨迹周期Tr=1.5s,并且两者波形不一致.实验结果如图6所示,从图6(a)可以看出参考轨迹的波形在第5个步态周期后基本跟上了期望轨迹,从图6(b)可以看出参考轨迹的周期在第5个步态跟上了期望轨迹的周期,而在第10个步态后达到稳定值.从图6(c)均方根误差曲线来看,参考轨迹与期望轨迹的偏差程度从初始的0.45左右降到了0.06以下.在这过程中均方根误差还出现了一段小小的波动,根据实验2)的分析可以知道,这个小的波动是周期超调导致的.把实验3)和前两个实验对比分析,可以看出在波形和周期都不确定的情况下,参考轨迹的自适应时间有所增加.

图5 条件2)下的周期自适应结果Fig.5 The period adaptation results on condition 2)

图6 条件3)下的步态轨迹自适应结果Fig.6 The gait trajectory adaptation results on condition 3)

4 结论

无论是外骨骼式还是末端牵引式的康复机器人,在康复训练时都需要设定相应的参考轨迹,由于人体步态轨迹差异性的存在,设计具有个性化以及可调整的步态参考轨迹显得尤为重要.在已有的步态轨迹自适应算法基础上,本文以高斯核函数的非线性振荡器为基础,利用轨迹偏差实现参考轨迹波形的自适应,另外为了使参考轨迹周期适应人体期望轨迹周期而提出了一种相位偏差曲线面积法.在建立的仿真模型基础上,分别验证了参考轨迹波形和周期自适应算法的可行性.实验结果表明,本文提出的自适应算法能在不同的初始条件下实现从初始参考轨迹到期望轨迹的调整,这对于康复机器人的临床运用具有重要意义.另外,虽然本文的方法是针对下肢康复机器人参考轨迹的自适应而提出的,但该方法不限于康复类机器人,也可以运用于假肢或外骨骼助行机器人的步态轨迹设计.下一步将在实际的下肢康复机器人平台上,分别以健康人和患者为实验对象实现参考轨迹的自适应.在临床运用中,可能需要根据患者的实际情况对算法做一些调整.比如当检测到患者出现肌肉痉挛或者肌肉疲劳时,需要对算法做相应的改变以防止参考轨迹的过度修正而对患者造成二次损伤.此外,该方法只运用了轨迹的误差信息,为了提高该算法的性能,可以加入能直观反映患者运动意图的信息,如人机交互力和肌肉表面电信号等.

1 Bourbonnais D,Noven S V.Weakness in patients with hemiparesis.American Journal of Occupational Therapy,1989,43(5):313−319

2 Barbeau H,Ladouceur M,Norman K E,Ppin A,Leroux A.Weakness in patients with hemiparesis:evaluation, treatment,and functional recovery.Archives of Physical Medicine and Rehabilitation,1999,80(2):225−235

3 Teasell R W,Kalra L.What's new in stroke rehabilitation.Stroke,2004,35(2):383−385

4 Dobkin B H.Strategies for stroke rehabilitation.The Lancet Neurology,2004,3(9):528−536

5 Huo W G,Mohammed S,Moreno J C,Amirat Y.Lower limb wearable robots for assistance and rehabilitation:a state of the art.IEEE Systems Journal,2016,10(3):1068−1081

6 Marchal-Crespo L,Reinkensmeyer D J.Review of control strategies for robotic movement training after neurologic injury.Journal of Neuroengineering and Rehabilitation,2009,6(1):Article No.20

7 Chen G,Chan C K,Guo Z,Yu H Y.A review of lower extremity assistive robotic exoskeletons in rehabilitation therapy.Critical Reviews in Biomedical Engineering,2013,41(4−5):343−363

8 Veneman J F,Kruidhof R,Hekman E E G,Ekkelenkamp R,Van Asseldonk E H F,van der Kooij H.Design and evaluation of the LOPES exoskeleton robot for interactive gait rehabilitation.IEEE Transactions on Neural Systems and Rehabilitation Engineering,2007,15(3):379−386

9 Jezernik S,Colombo G,Morari M.Automatic gait-pattern adaptation algorithms for rehabilitation with a 4-DOF robotic orthosis.IEEE Transactions on Robotics and Automation,2004,20(3):574−582

10 Banala S K,Kim S H,Agrawal S K,Scholz J P.Robot assisted gait training with active leg exoskeleton(ALEX).IEEE Transactions on Neural Systems and Rehabilitation Engineering,2009,17(1):2−8

11 Zanotto D,Stegall P,Agrawal S K.Adaptive assist-asneeded controller to improve gait symmetry in robotassisted gait training.In:Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA).Hong Kong,China:IEEE,2014.724−729

12 Aoyagi D,Ichinose W E,Harkema,S J,Reinkensmeyer D J,Bobrow J E.A robot and control algorithm that can synchronously assist in naturalistic motion during body-weightsupported gait training following neurologic injury.IEEE Transactions on Neural Systems and Rehabilitation Engineering,2007,15(3):387−400

13 Hesse S,Uhlenbrock D.A mechanized gait trainer for restoration of gait.Journal of Rehabilitation Research and Development,2000,37(6):701−708

14 Schmidt H,Werner C,Bernhardt R,Hesse S,Krger J.Gait rehabilitation machines based on programmable footplates.Journal of Neuroengineering and Rehabilitation,2007,4(1): 218−227

15 Banala S K,Agrawal S K,Scholz J P.Active leg exoskeleton (ALEX)for gait rehabilitation of motor-impaired patients. In:Proceedings of the 10th International Conference on Rehabilitation Robotics.Noordwijk,Netherlands:IEEE,2007. 401−407

16 Wheeler J W,Krebs H I,Hogan N.An ankle robot for a modular gait rehabilitation system.In:Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems.Sendai,Japan:IEEE,2004. 1680−1684

17 Emken J L,Harkema S J,Beres-Jones J A,Ferreira C K, Reinkensmeyer D J.Feasibility of manual teach-and-replay and continuous impedance shaping for robotic locomotor training following spinal cord injury.IEEE Transactions on Biomedical Engineering,2008,55(1):322−334

18 Hocoma.Lokomat[Online],available: https://www. hocoma.com/world/en/media-center/media-images/lokomat/,June 27,2016

19 Vallery H,van Asseldonk E H F,Buss M,van der Kooij H.Reference trajectory generation for rehabilitation robots: complementary limb motion estimation.IEEE Transactions on Neural Systems and Rehabilitation Engineering,2009,17(1):23−30

21 Ijspeert A J.Central pattern generators for locomotion control in animals and robots:a review.Neural Networks,2008,21(4):642−653

22 Seo K,Hyung S,Choi B K,Lee Y,Shim Y.A new adaptive frequency oscillator for gait assistance.In:Proceedings of the 2015 IEEE International Conference on Robotics and Automation(ICRA).Seattle,Washington,USA:IEEE,2015.5565−5571

23 Ronsse R,Vitiello N,Lenzi T,van den Kieboom J,Carrozza M C,Ijspeert A J.Human-robot synchrony:fexible assistance using adaptive oscillators.IEEE Transactions on Biomedical Engineering,2011,58(4):1001−1012

24 Gams A,Ijspeert A J,Schaal S,LenariJ.On-line learning and modulation of periodic movements with nonlinear dynamical systems.Autonomous Robots,2009,27(1):3−23

25 Righetti L,Buchli J,Ijspeert A J.Dynamic Hebbian learning in adaptive frequency oscillators.Physica D:Nonlinear Phenomena,2006,216(2):269−281

26 Karnjanaparichat T,Pongvuthithum R.Synchronization control scheme for gait training robot and treadmill.In:Proceedings of the 2014 International Computer Science and Engineering Conference(ICSEC).Khon Kaen,Thailand: IEEE,2014.481−485

28 Hogan N.Impedance control:an approach to manipulation: Part II-implementation.Journal of Dynamic Systems, Measurement,and Control,1985,107(1):8−16

罗林聪中国科学院自动化研究所复杂系统管理与控制国家重点实验室控制科学与工程专业博士研究生.主要研究方向为康复机器人控制.

E-mail:luolincong2014@ia.ac.cn

(LUO Lin-CongPh.D.candidate in control science and engineering at the State Key Laboratory of Management and Control for Complex Systems,Institute of Automation, Chinese Academy of Sciences.His main research interest is rehabilitation robot control.)

侯增广中国科学院自动化研究所研究员.主要研究方向为机器人控制,智能控制理论与方法,医学和健康自动化领域的康复与手术机器人.本文通信作者.

E-mail:zengguang.hou@ia.ac.cn

(HOU Zeng-GuangProfessorat the State Key Laboratory of Management and Control for Complex Systems,Institute of Automation,Chinese Academy of Sciences.His research interest covers robotics,intelligent control with applications to rehabilitation,surgical robots for medical and health automation.Corresponding author of this paper.)

王卫群中国科学院自动化研究所复杂系统管理与控制国家重点实验室副研究员.主要研究领域为康复机器人,人机动力学,人-机交互控制,生物电信号处理.

E-mail:weiqun.wang@ia.ac.cn

(WANGWei-QunAssociate professor at the State Key Laboratory of Management and Control for Complex Systems,Institute of Automation,Chinese Academy of Sciences.His research interest covers rehabilitation robot,dynamics of human-robot system,human-robot interaction control,and biomedical signal processing.

彭 亮中国科学院自动化研究所复杂系统管理与控制国家重点实验室助理研究员.主要研究方向为机器人控制,生物信号处理.E-mail:liang.peng@ia.ac.cn

(PENG LiangAssistant professor at the State Key Laboratory of Management and Control for Complex Systems,Institute of Automation,Chinese Academy of Sciences.His research interest covers robotics and biomedical signal processing.)

A Gait Trajectory Adaptation Algorithm Based on Nonlinear Oscillator

LUO Lin-Cong1,2HOU Zeng-Guang1,3WANG Wei-Qun1PENG Liang1

Gait trajectory is an important factor to the efects of rehabilitation with adaptability has great signifcance for clinical application of lower limb rehabilitation robot.The oscillator can output various waveforms and periodic smooth signals by adjusting parameters online,which is frequently used to generate gait reference trajectory for rehabilitation robots.This paper proposes a gait trajectory adaptation algorithm for lower limb rehabilitation robot based on Gaussian kernel nonlinear oscillators.In the algorithm,trajectory deviation is used to adjust the waveform of reference trajectory, and the area of phase deviation curve is used to adjust the period of reference trajectory.Firstly,the paper introduces the nonlinear oscillator model for generating gait reference trajectory.Then,the adaptation algorithms for gait trajectory waveform and period are described based on this mathematical model.Finally,a human-robot simulation model is built based on a weight supporting rehabilitation robot system.These algorithms are validated by simulation experiments and the results demonstrate the feasibility of proposed algorithms.

Lower limb rehabilitation robot,gait trajectory,oscillators,adaptive algorithm,gait training

罗林聪,侯增广,王卫群,彭亮.一种基于非线性振荡器的步态轨迹自适应算法.自动化学报,2016,42(12): 1951−1959

Luo Lin-Cong,Hou Zeng-Guang,Wang Wei-Qun,Peng Liang.A gait trajectory adaptation algorithm based on nonlinear oscillator.Acta Automatica Sinica,2016,42(12):1951−1959

2016-03-02 录用日期2016-10-14

Manuscript received March 2,2016;accepted October 14,2016

国家自然科学基金(61225017,61421004,61533016),中国科学院先导科技专项(XDB02080000),北京市科技计划(Z161100001516004)资助

Supported by NationalNaturalScience Foundation of China(61225017,61421004,61533016),StrategicPriority Research Program oftheChineseAcademy ofSciences (XDB02080000),and Beijing Science and Technology Project (Z161100001516004)

本文责任编委王启宁

Recommended by Associate Editor WANG Qi-Ning

1.中国科学院自动化研究所复杂系统管理与控制国家重点实验室北京100190 2.中国科学院大学北京100049 3.中国科学院脑科学与智能技术卓越创新中心北京100190

1.State Key Laboratory of Management and Control for Complex Systems,Institute of Automation,Chinese Academy of Sciences,Beijing 100190 2.University of Chinese Academy of Sciences,Beijing 100049 3.CAS Center for Excellence in Brain Science and Intelligence Technology,Chinese Academy of Sciences,Beijing 100190