空间滞后误差自相关随机前沿模型参数的估计
2017-01-09窦剑军张辉国胡锡健新疆大学数学与系统科学学院乌鲁木齐830046
窦剑军,张辉国,胡锡健(新疆大学 数学与系统科学学院,乌鲁木齐 830046)
空间滞后误差自相关随机前沿模型参数的估计
窦剑军,张辉国,胡锡健
(新疆大学 数学与系统科学学院,乌鲁木齐 830046)
文章利用工具变量矩阵方法研究了空间滞后误差自相关随机前沿模型参数的估计问题,得到了参数估计的表达式。与极大似然估计相比较,工具变量矩阵法极大地简化了计算。蒙特卡罗模拟的结果表明,参数估计值十分逼近真值。
空间滞后误差自相关模型;随机前沿模型;工具变量矩阵;蒙特卡罗模拟
0 引言
随着产业经济学中投入-产出理论的深入发展,生产者越来越关注生产过程中的技术效率问题。作为技术效率测算的参数方法的随机前沿模型被广泛地应用于效率的测算中,该方法最早由Aigner、Lovell和Schmidt、Meeusen[1]和Van den Broeck[2]和Battese&Corra[3]三组研究人员于1977年同时独自提出。其基本思想和理论依据归结为:以盈利为目的的生产者追求的是利润的最大化,但是在实际的生产过程中,由于管理水平的不同以及其他一些因素,并不是所有的生产单元都能达到生产前沿面上,也就是厂商的产出未必能实现利润最大化,而是与前沿面有一个“垂直”的距离。在随机前沿模型的设定中,这一差异用技术无效率项和外生的随机扰动项来表示。所谓技术无效率项是指在给定的投入水平下,由于企业在生产过程中的各种管理不严和生产者个人技术问题引起生产过程中技术没有得到最大的发挥,企业生产者没有达到最大可能的产出,刻画的是某些生产单元位于前沿面下的事实;而外生的随机扰动是指不可控制的随机因素,例如天气、运气、测量误差等。
在以查尔斯·W·柯布和保罗·H·道格拉斯建立的C-D生产函数为基础的随机前沿模型中,其基本假定是不同生产单元之间相互独立,并不考虑它们的相互效应。但是在许多情况下,特别是涉及到区域经济研究、技术扩散过程中,地理位置上的邻接关系在生产单元之间起着至关重要的作用,生产单元相互独立的假设存在很大的缺陷。随着经济全球化的深入发展和区域之间经济合作的不断加强,任何一个国家或地区其经济发展都相互借鉴,进行全方位的经济合作和文化À流。当外生不确定性因素影响一个国家经济时,其影响以一定的方式进行扩散,影响到其他有经济合作关系的国家或地区,例如2008年美国爆发的金融危机。
近年来,空间计量经济学作为计量经济学的一个全新分支,其理论研究和实证分析迅速发展。空间结构关系成为空间计量经济学模型的一个重要组成部分,将空间效应引入经典计量和统计方法中,并广泛地应用于计量经济学、地理学、传染病学等诸多领域。如果存在空间的À互作用,但随机前沿模型中没有引入空间结构,仍然假设生产单元之间相互独立并对其技术效率做出定量分析,势必会掩盖空间层面和地理位置上的相互作用,从而导致参数估计和技术效率推断有偏。国内外将空间影响关系和随机前沿模型相结合的研究相对较少,开创性地将空间相互影响和随机前沿分析相结合的工作来自Druska和Horrace (2004)[4],随后国内也开始了空间随机前沿模型的研究工作。本文采用横截面数据,建立了空间滞后误差自相关随机前沿模型,同时考虑因变量在地理位置上的滞后和误差的空间相关性,用二阶段最小二乘法和矩估计方法估计空间滞后误差自相关随机前沿模型,具体来说,该方法首先选择工具变量矩阵对因变量的空间滞后作回归,这样因变量的空间滞后就和随机扰动项不相关,然后采用二乘法求参数的估计。相对于极大似然估计法无法得到参数的解析解,只能用迭代算法,该方法有效地解决了空间滞后误差自相关随机前沿模型的估计问题。
1 空间滞后误差自相关随机前沿模型的估计问题
待估计的模型为:
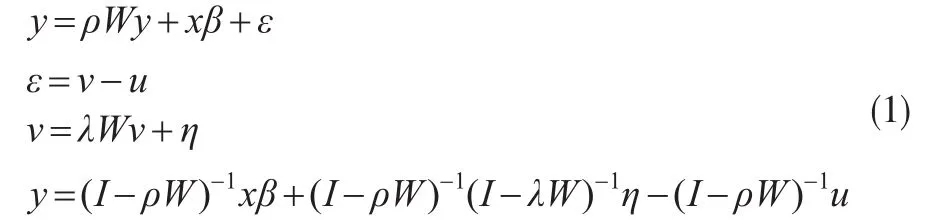
其中,y为因变量,x为自变量;β为回归系数;u为技术无效率向量;v为误差项,η为随机干扰项向量;W是空间权重矩阵,Wy为因变量的空间滞后,Wv为误差项空间滞后;ρ是待估计的空间自回归系数;λ是待估计的空间误差自相关系数。
在本文中假设技术无效率项ui~i.i.d.N+(0,σ2u),随机干扰项ηi~i.i.d.N(0,σ2e)。
ηi和ui相互独立且和自变量x之间不相关。对模型(1)进行极大似然估计,u的分布密度函数为:

因为η~N(0,σ2eI),ν=(I-λW)-1η根据正态分布的性质:

可得v的分布密度函数为:

由于u和v不相关,可得(u,v)的联合分布密度函数:
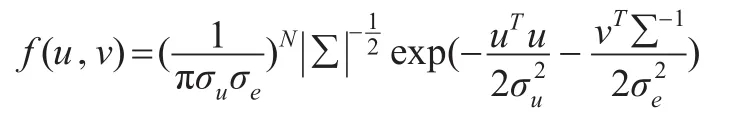
由ε=ν-u,根据二元变换定理可知(u,ε)的联合分布密度函数为:

然后将 f(u,ε)对u积分得到ε的边际分布密度函数:

由于ε=(I-ρW)y-xβ,基于式(2),可得到模型(1)的对数似然函数:

在上式对每个参数求偏导,令一阶导数等于0无法得到参数的解析解,因为计算过程涉及到概率密度函数和累计分布函数。如果直接用修正的最小二乘法(COLS)估计,首先要用普通最小二乘(OLS)方法估计式(1),但是,由于:

其中,A=I-ρW,在一般情况下,式(4)不等于0,即意味着误差项ε与Wy之间存在相关性,采用OLS方法估计模型(1)不满足高斯-马尔科夫条件,这样违背基本假设的估计值不是一致估计值,从而导致第二步的修正没有意义。
2 二阶段最小二乘和矩估计方法
通过上面的分析可知,修正最小二乘方法无法估计空间滞后误差自相关随机前沿模型的原因在于该方法的基本假定条件不成立。这样一个很自然的问题就是,如果通过工具变量矩阵做回归满足基本假定条件,是否可以得到参数的一致估计量?根据最小二乘原理,答案是肯定的,至此,接下来的问题就是如何用工具变量矩阵作回归满足基本假定条件,再用最小二乘法得到参数ρ,β(不含常数项)和λ的一致估计量;在第二阶段,由εˆ根据矩估计(MEE)得到σ2u和σ2e的一致估计,并对截距项进行修正。
待估计的模型为:

因为ν=λWν+η,可得ν=(I-λW)-1η,将ε=ν-u带入式(1)可得:

根据Lesage(2009)[5]的方法:

在这里只取前两项并带入式(5)得:
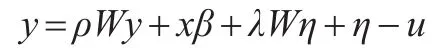
令ε=η-u,则模型可变为:

为表达方便,将模型(6)表示为:

其中,Z=(Wy,x,Wη),δ=(ρ,β,λ)T
由于变量存在内生性问题,无法直接对式(7)进行估计,一个有效的解决途径是通过构建工具变量矩阵Q对空间滞后因变量作回归得到的一致估计量:
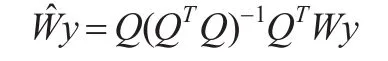
然后用Zˆ=(Wˆy,x,Wη)带入式(7),求得δ的2SLS估计量:

在上述求解过程中,一个重要的问题是工具变量的选择,在这里由于x和Wη共生Wy,所以在选择工具变量矩阵是应同时考虑x和Wη的作用。对模型(6)进行变形得:
(I-ρW)y=xβ+λWη+ε,进一步有:
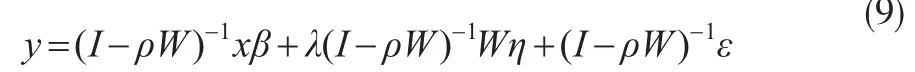
其中根据(I-ρW)-1=I+ρW+ρ2W2+ρ3W3+…并带入式(9)有:

所以工具变量矩阵选择为Q=[x,Wx,Wη,W2η]
另外一个问题是,对于空间滞后误差自相关随机前沿模型,采用式(8)得到常数项的估计值不是一致估计量。因为误差项ε中同时包含了对称的双边误差项η和非对称的单边非效率项u的均值的共同效应。
为了得到σe2和σu2的一致估计量,将第一阶段的估计量δ2SLS带入式(7),得到ε的残差项,以为基础,构建相应的二阶和三阶样本矩:
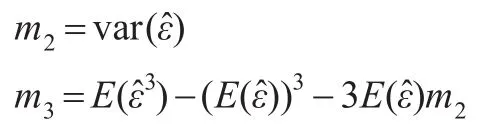
根据Olsen等(1980)[6]的方法,σ2u与σ2e的一致估计量为:


3 技术效率的估计
上述模型的参数估计是随机前沿模型估计的第一步,第二步是对生产单元进行技术效率的推断,找到技术无效率的生产单元,并评价无效率的程度。Jondrow、Lovell and Materovi等(JLMS)(1982)[7]指出各个生产单元的技术效率项ui可以通过E(ui|εi)或Mode(ui|εi)来估计,第i个生产单元的技术效率TEi=exp{-ˆi},其中ˆi=E(ui|εi)或Mode (ui|εi)。为此需要得到 f(u|ε),根据条件概率分布:

其中μ和Ω定义前面已经给出,易见 f(u|ε)服从N元截尾正态分布N+(μ,Ω),估其众数为:
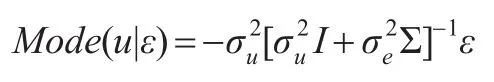
因此,一旦求出u的点估计,各生产单元的技术效率估计可表达为:

4 蒙特卡罗模拟
考虑如下数据数据生成过程:

其中ui~i.i.d.N+(0,0.82),ηi~i.i.d.N(0,0.22),(β0,β1,β2, β3)=(4,5,6,7),解释变量x1,x2和x3均服从标准正态分布,将 ρ的取值固定为0.5,误差自相关系数 λ考虑-0.9,-0.7,-0.5,-0.3,-0.1,0,0.1,0.3,0.5,0.7,0.9共11种情况。空间权重矩阵取为Rook规则型权重矩阵和Queen规则型权重矩阵,每种权重矩阵经过行标准化处理,考察的样本量为N=196,400,模拟次数均为50次。结果见表1和表2。

表1 Rook型权重矩阵估计结果
从表1可以看出,ρ,β0,β1,β2,β3的估计值不随λ的变化而变化,当样本量为196时ρ,β0,β1,β2,β3的估计值已经非常接近真值,当样本量增大时,这几个值没有显著的变化,但σu2,σe2的估计值当样本量增大时,估计值越来越接近真实值。λ的估计值有一点的偏差但偏差不大,基本接近真实值。

表2 Queen型权重矩阵估计结果
从表2可以看出,ρ,β0,β1,β2,β3的估计值和Rook型权重矩阵一样,仍然不随λ的变化而变化,在样本量为196时,ρ,β0,β1,β2,β3的估计值已经非常接近真实值,所以当样本量增大时,变化不是很大,但是σu2,σe2的估计值随样本量的增大越来越靠近真实值,λ的估计值和真实值有一点偏差但不大,基本接近真实值。
5 结论与展望
本文构建了半正态空间滞后误差自相关随机前沿模型,用二阶段最小二乘法和据估计方法对该模型进行了估计,得到了参数估计的表达式,该方法有效地解决了极大似然估计模型无法得到参数解析解只能用近似迭代算法的问题。蒙特卡罗模拟的结果表明,本文采用的方法对模型有很好的估计。
本文仅考虑了误差的空间自相关性的情况,没有考虑技术无效率项的空间自相关性。如何对空间滞后误差和技术无效率空间自相关模型作估计还需进一步的研究,对技术无效率项还可以作其他形式的假定,以及模型的具体应用还需进一步的讨论。
[1]Aigner D,Lovell K,Schmidt P.Formulation and Estimation of Sto⁃chastic Frontier Production Function Models[J].Journal of Econo⁃metrics,1977,(6).
[2]Meeusen W,van den Broeck J.Effciency Estimation From Cobb-Douglas Production Functions With Composed Error[J].International Economic Review,1977,(18).
[3]Battese G,Corra G.Estimation of a Production Frontier Model:With Application to the Pastoral Zone of Eastern Australia[J].Australian Journal of Agricultural Economics,1977,(21).
[4]Druska V,Horrace W.Generalized Moments Estimation for Spatial Panel Data:Indonesian Rice Farming[J].American Journal of Agricul⁃tural Economics,2004,86(1).
[5]James Le Sage,Robert K.Pace:Introduction to the Spatial Economet⁃rics[J].Statistical Papers,2011,52(2).
[6]Olson J,Schmidt P,Waldman D.A Monte Carlo Study of Estimators of the Stochastic;Frontier Production Function[J].Journal of Econo⁃metris,1980,13(1).
[7]Jondrow J,Lovell K,Materov I,et al.On the Estimation of Technical Ineffciency in the Stochastic Frontier Production Function Model[J]. Journal of Econometrics,1982,(19).
(责任编辑/易永生)
F222
A
1002-6487(2016)24-0004-03
国家自然科学基金资助项目(41261087);教育部人文社会科学青年研究项目(12XJJC91001);新疆大学博士启动基金资助项目(BS130103)
窦剑军(1987—),男,甘肃白银人,硕士研究生,研究方向:空间统计学、空间计量经济学。
