二次损失下带约束的增长曲线模型的Minimax估计

王理峰，朱道元(.南京铁道职业技术学院 社科部，南京003;.东南大学 数学系，南京 0096)

二次损失下带约束的增长曲线模型的Minimax估计

王理峰1，朱道元2
(1.南京铁道职业技术学院 社科部，南京210031;2.东南大学 数学系，南京 210096)

文章对于带椭球约束的增长曲线模型，在二次损失函数下给出回归系数在线性估计类中的Mini⁃max估计，证明该估计是压缩有偏、可容许估计。在一些特殊的情形下，该估计包括了增长曲线功效岭回归估计、多元线性Minimax估计等。

增长曲线模型；Minimax估计；二次损失函数；椭球约束

0 引言

Minimax估计是一类重要的估计，它使极大风险极小化，是避免损失的一种选择，因此在实际生活中有重要的用途。用Minimax原理来估计模型的回归系数最早由Kuks和Olman(1971，1972)提出，之后有许多学者用这种原理来研究模型的估计和预测问题。Minimax估计与损失函数和所考虑的估计类有关，主要是在矩阵损失与二次损失函数下，在齐次线性估计类和非齐次线性估计类中展开的。但实际应用中总是对参数有或多或少的认识，会得到一些约束条件。谭萄[1]和高婷婷[2]给出了带等式约束的多元回归系数线性估计在齐次线性估计类中的Minimax估计。周明华[3]在矩阵损失函数下，研究带椭球约束的增长曲线模型中回归系数的线性Minimax估计。HelgeBlaker[4]讨论二次损失下带约束的线性回归模型的线性Minimax估计。椭球约束下增长曲线模型的Minimax估计并不能通过拉直后利用HelgeBlaker的结论得到。本文将研究二次损失下带椭球约束的增长曲线的Minimax估计，一定意义上这也是将HelgeBlaker的主要结果推广到了增长曲线情形。

为了计算方便，将介绍几个符号及引理：

符号1[5]:a∨b=max(a，b),a∧b=min(a，b),x+=max(x，0)

若A为n×n阶对称矩阵，有谱分解A=PDP'，其中P为n×n阶正À阵，D为对角阵，其对角元记为di，i=1，2，…，n。定义 A+=PD+P′，其中 D+=diag((d1∨0)，…(di∨0)，…(dn∨0))。

引理1[5]:A⊗(B1+B2)=A⊗B1+A⊗B2,(A1⊗B1)(A2⊗B2)=(A1A2)⊗(B1B2),tr(A⊗B)=trA·trB

引理2[5]:E(xAx)=u'Au+tr(AΣ)，其中Ex=u，var(x)=Σ。

证明：参见文献[5]

引理4:对于线性模型y=Xβ+e，E(e)=0，cov(e)=σ2∑，∑＞0。若rk(Xn×p)=p，则ˆ～Cβ⇔A(X'∑-1X)-1A'≤A(X'∑-1X)-1C'

证明：参见文献[5]

本文采用的二次损失函数为L(Bˆ，B，A)=tr(Bˆ-B)'A (Bˆ-B)，A为 p×p阶正定阵，其相应的风险函数为EL(Bˆ，B，A)。

1 模型准备

其中Y为n×q阶观测矩阵，X1，X2为n×p，t×q阶设计矩阵且rk(X1)=p，rk(X2)=t。E=(e1…eq)为n×q阶误差矩阵，W=(wij)为已知的q阶非零非负定阵。B为 p×t阶未知参数矩阵，满足椭球约束tr(X2'B'X1'FX1BX2)≤ρ，其中F为n×n阶非负定阵。记≤ρ}，模型（1）的最小二乘估计为：

1．1 增长曲线模型典则化

增长曲线模型的估计问题，在典则形式下变的易理解。下面将把模型（1）化为典则形式。

对X1进行奇异值分解，其中U1、V1分别为n×n、p×p阶正À阵，为n×p阶矩阵。的(i，i)元为，其余位置为0，则：其中的非零特征根，其中

同理对X2进行奇异值分解U2、V2分别为t×t、q×q阶正À阵，为t×q阶矩阵，的(i，i)元为其余位置为0，则其中为的非零特征根，其中

模型（2）的最小二乘估计为:

1．2 将模型进一步简化处理

为使tr(B'X'FXB)、L(ˆ，B，A)能化为简洁形式，须规定A、F、W满足条件1：

估计R只需考虑模型（3）即可，而模型中D1，D2为对角阵，这样问题就变得简洁，易求。将模型（3）拉直得：

参数约束空间可简化为：

损失函数可简化为:

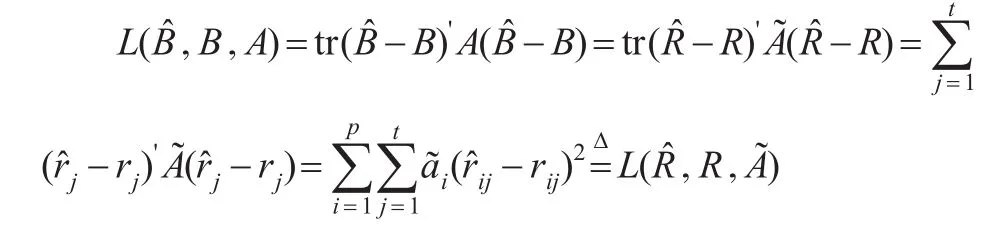
2 椭球约束下增长曲线模型的Minimax估计的求解

对于模型（3）有：

定理1：将模型（3）写成元素形式为：

则模型（3）的Minima风险为：

其中ς表示所有p×p阶矩阵组成的类，τ表示所有t×t阶矩阵组成的类，

证明：（1）首先证明使极大风险极小化的K，L是对角矩阵，本文利用Speckman[6]的思路来讨论。记KL的 (i，j)元为

取R满足：i≠m，j≠n时，rij=0。则：

所以：

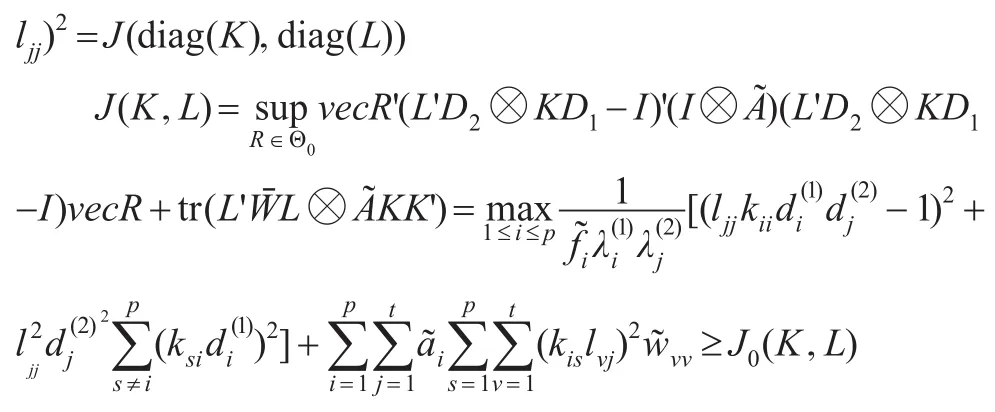
当且仅当矩阵K，L为对角阵时上面等号成立。即证明了使极大风险极小化的矩阵K，L是对角阵。

显然ν2在约束条件边界上达到。下面利用Lagrange乘子法求ν2：

对于 h＞0，i=1，…，p， j=1，…，t，记 G(R，h)=则

当kilj=(kilj)*，i=1，…，p，j=1，…，t时，上面不等式仍成立。而：

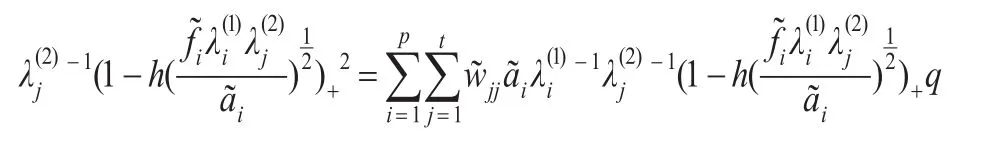
由上面的不等式及证明中的(1)部分可知：

由定义1知(kilj)*zij为rij的Minimax估计。即ˆM，ij= (kilj)*zij，i=1，…，p， j=1，…，t

综上即证定理。

由上面的定理容易得到本文的主要定理：

定理2：对于增长曲线回归模型(1)，B∈Θ={B| tr(X2' B'X1'FX1BX2)≤ρ}，F满足条件1，则 β=νec(B)的线性Minimax估计为：其中h满足:

令ς表示任意的p×n阶矩阵组成的类，τ表示任意的q×t阶矩阵组成的类。则线性Minimax估计的风险为：

证明：由前面的变换知：

则：

由定理1知：

写成矩阵形式为：

下面证明νecBˆM为νecB的线性Minimax估计：为R的线性Minimax估计，由定义1知

综上即证定理。

3 增长曲线Minimax估计的性质

增长曲线Minimax估计具有以下性质：

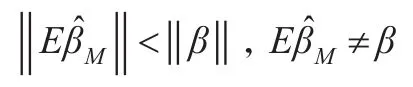
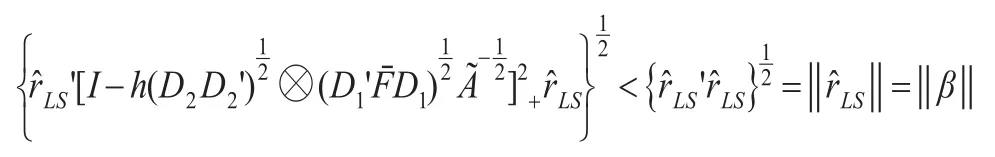
显然成立。

而β=(V2⊗V1)r，由引理3知ˆM是β的可容许估计。

4 增长曲线Minimax估计的特例

例2：当 X2X2'=I时，其中h满足：其Minimax风险为：

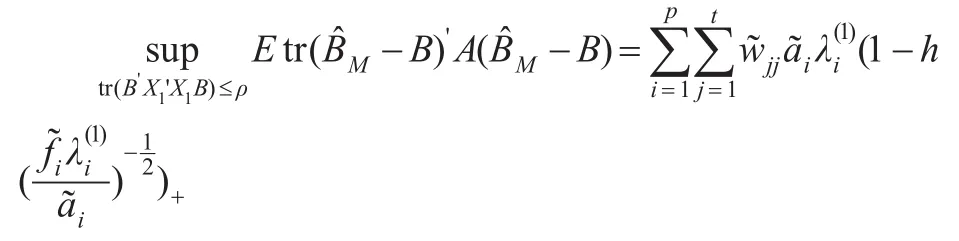
该结果与文献[7]所求的多元线性模型的Minimax估计结果一致。

[1]谭萄.多元回归系数线性估计的Minimax可容许性[J].广西师范大学学报，2001，19(1).

[2]高婷婷，田丽.矩阵损失下带约束的多元回归系数的Minimax估计[J].安徽师范大学学报(自然科学版),2009,32(1).

[3]周明华等.受椭球约束回归系数在矩阵损失下的线性Minimax估计[J].浙江工业大学学报,1998,26(3).

[4]Blaker H.Minimax Estimation in Linear Regression Under Restric⁃tions[J].Journal of Statistical Planning and Inference,2000,(90).

[5]王松桂.线性模型的理论及其应用[M].合肥：安徽科技出版社, 1987.

[6]Speckman P,Spline Smoothing and Optimal Rates of Convergence in Nonparametric Regression Models[J].Annals of Statistics,1985,(13).

[7]王理峰,朱道元.有约束的多元线性回归模型的Minimax估计[J].重庆工商大学学报（自然科学版）,2009,26(6).

（责任编辑/易永生）

O212.1

A

1002-6487（2016）24-0007-05

王理峰（1981—），女，河南平顶山人，硕士,讲师，研究方向：多元统计分析。（通讯作者）朱道元（1947—），男，江苏扬州人，教授，研究方向：多元统计分析与数学建模。