抽样调查校准估计法应用研究

李国正，张明玺，谢艾香(1.北京工业大学 a.经济与管理学院,b.应用数理学院 北京10014；.北京大学 光华管理学院，北京 100871)

抽样调查校准估计法应用研究

李国正1a，张明玺2，谢艾香1b
(1.北京工业大学 a.经济与管理学院,b.应用数理学院 北京100124；2.北京大学 光华管理学院，北京 100871)

文章归纳梳理了抽样调查校准估计法的理论发展，对最短距离法、工具向量法和参数校准法的基本理论与操作进行了对比分析。在此基础上，进一步对抽样调查的两阶段校准估计法原理及应用进行了分析，并选取了我国混合所有制经济国有企业中进行了国企产权改革的企业为样本，并基于这三种校准估计方法得到混合所有制国企产权改革的绩效数据与实际的绩效数据进行了比较，以判断抽样调查校准估计方法的有效性。研究发现，从均方误差和相对偏差的角度来看，最短距离法、工具向量法和参数校准法这三种抽样调查校准估计法都能很好的估计混合所有制国企产权改革绩效，但参数校准法更加有效。

抽样调查；校准估计法；混合所有制；国企产权改革；国企绩效

0 引言

在抽样调查中，样本结构与总体结构会存在着偏差。不管这些偏差是基于何种原因产生，都会影响抽样调查的精度和效度。当调查指标与目标量高度相关时，此时样本结构与总体结构的偏差若较大，会影响目标估计量的估计结果。此时，若要更好地估计出总体的相关信息并提高估计结果的精度，需要对调查样本结构进行调整。此时，校准估计法即利用现有的已知调查总体的辅助信息，在一定的约束条件下对样本进行调整，并使得样本结构尽量拟合总体结构估计方法。校准估计方法可以很好的减少样本总体与结构总体的差异性，提高抽样精度和偏差以及估计精度。

自从Deville and Sarndal（1992）提出校准估计量方法以来，大量的文献对这一研究方法进行了研究。现有对校准估计法的研究目前仍处于不断发展中，也在国外的抽样实践中得到了相对较好的应用。但在我国，对校准估计量方法的理论研究相对较少，主要以学习较少为主，特别是实践应用方面相对较少。事实上，相对于经验研究中占据主导地位的计量实证方面，校准估计的作用远被低估。因此，本文将在对抽样调查校准估计的现有研究进行对比分析的基础上，利用两阶段校准估计法原理，以我国混合所有制国企产权改革绩效为研究对象，研究抽样调查校准估计法在我国具体实践中的应用问题。

1 抽样调查校准估计法理论发展

对于抽样调查校准估计法，基本思路如下：假设总体k的入选概率为πk，原始设计权重为

此抽样调查时，根据相关的辅助信息对原始设计权重不断调整，形成新的校准权重wk。在这种情形下，新的样本结构可以更好地拟合总体结构，从而使得估计的精度得到提高。

现阶段，校准估计法主要有以下三种方法：

1．1 最短距离法

为了使得距离函数最小，最短距离法试图利用新的校准权重wk来代替原始设计权重dk以达到这一目标。令辅助变量集合xk=(xk1，...，xkj，...，xkJ)′，其中k∈s。总体X=(x1，x2，...，xJ)为已知参数。令原始设计权重与校准权重之间的距离定义为G(wk，dk)，为一个包含了比例因子qk的函数，其中qk＞0。令G(w ，d)对w的偏导g(w ，d)连续可微且g(0 ，0)=0。通常来讲，距离函数需要满足gk(w ，d)=是一个严格单调递增的函数，且满足g(1)=0， g′(1)=1。

对于最短距离法而言，其目标在于抽样调查时搜寻到最接近原始设计权重dk的校准权重wk，使得在约束条件下能得到最小的值。基于Lagrange乘子法，可以得到校准权重和总体的校准估计量：

通常来讲，常见的距离函数包括以下几种，用表1来表示：

表1 常见的距离函数

校准估计法是利用距离函数，其校准估计量都渐进接近于广义的线性回归估计量，尽管不同的距离函数会导致校准估计量的方差有较小的变化。

1．2 工具向量法

为了得到无偏一致的校准估计量，有学者将最短举例法中的约束等式用包含两个参数的简单函数F(·)来表示，只需要校准权重wk满足这一函数即可（Estevao and Sarndal,2000,2006）。

假设辅助向量xk的IV定义为其中k∈s。矩阵是一个J×J维的非奇异矩阵。此时，校准权重将满足：

其中，F(·)和前面的最短距离法有同样的效果。而λ则由校准式子决定。当本文将F(·)的函数形式设定为1+u=1+λ′zk时，此时有进而可以得到：

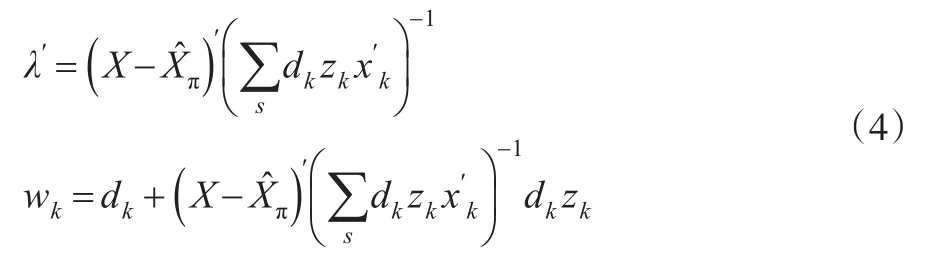
通常来讲，zk是xk的函数。工具向量可以表示为：

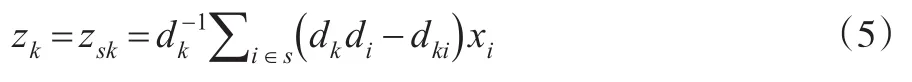
1．3 参数校准法

一般来讲，校准估计量会设定目标变量与辅助变量之间存在着线性关系，但若两者之间不存在线性关系时，此时得到的校准估计结果将À叉。为此，有学者提出了参数校准方法，利用模型估计的方法来解决这一问题（Wu and Sitter,2001）。具体来讲，其基本思路如下：当对于任何k∈U，xk是已知时，此时辅助信息是信息完全的，可以充分利用每个总体单位的所有辅助信息。

假设y与x之间满足以下关系：

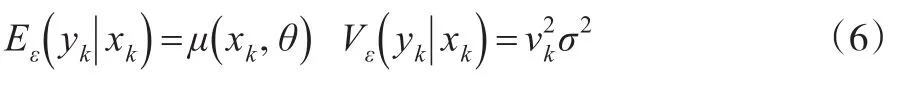
此时，总体的辅助信息可以用以拟合方程μ(xk，ˆ)，模型的校准估计量可以表示为：

相应的约束条件可以表示为：

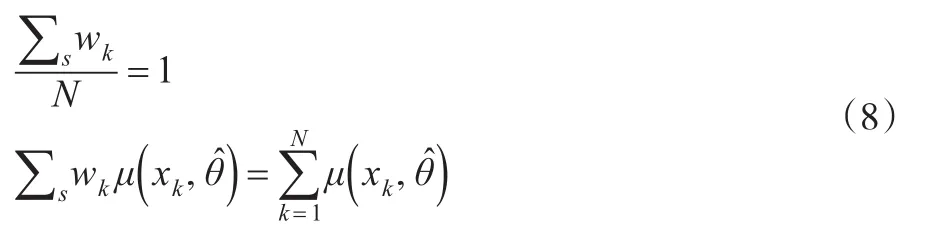
根据式（8）的约束条件可以得到校准权重。相应的卡方距离函数为

利用基于Lagrange乘子法：

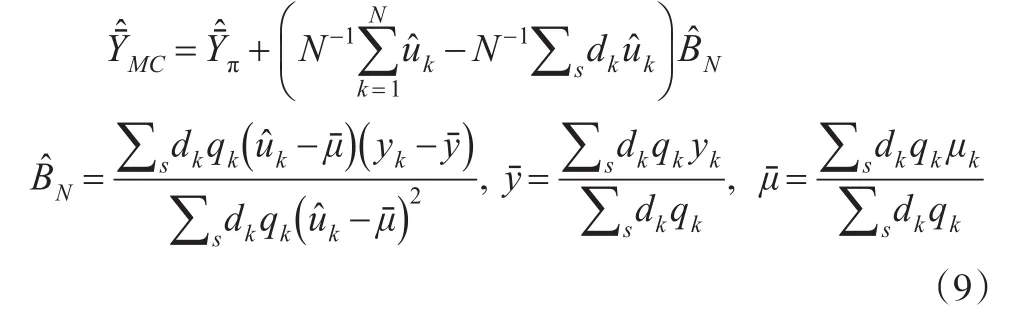
相应的，参数校准估计量的渐进方差以及其估计量可以表示为：

Rueda等（2010）利用非参数估计的方法，对有限总体分布函数进行了估计。具体来讲，基于局部线性Kernel回归来回归得到分布函数的校准估计量。

对比这三种方法，最短距离法是工具变量与参数校准法的一个特例。工具向量法和最短距离法相比，同样可以保证无偏与一致性，但其校准权重的得到方式更加多样化，并且其校准估计量也相对丰富。而参数校准法则可以解决总体目标变量与辅助变量之间的非线性问题，估计结果相对较好。同时，这三种方法对于辅助信息的要求程度也有较大不同。对于工具向量法和最短距离法而言，需要得到辅助变量的总体总值以及所有样本的辅助变量取值。而参数校准法对辅助信息的要求是最高的，还需要知道总体变量的总体总值以及所有总体单位的辅助变量取值。

2 抽样调查的两阶段校准估计法原理及应用

2．1 抽样调查的两阶段校准估计法原理

目前，校准估计法常用的是两阶段估计方法，其具体方法如下：

两阶段校准估计法的第一步是计算中间校准权重w1k，此时的校准约束条件可以表示为：

相应的中间校准权重为：

两阶段校准估计法的第二步是得到最终的校准权重wk，此时的校准约束条件可以表示为：

其中，zk是一个有效的IV。相应的校准估计量

2．2 两阶段校准估计法在混合所有制国企产权改革抽样调查中的应用

假设所有混合所有制企业的样本总体为U={1，...，k，...，N}，存在N1个单元，分别为U1，...，Ui，...，UN1。此时，两阶段抽样过程如下：

第一步，依据抽样方案 pI(·)，从U1中抽取初始单元样本sI，后者在抽样方案pI(·)中的概率为抽样方案πIi，

对于混合所有制国企产权改革，本文将群i的目标变量y(c)i的辅助变量为x(c)i。因此，对于总体k的目标变量y(u)k的辅助变量为x(u)k。此时，两阶段抽样的辅助信息包括两个方面的信息：（1）群水平。任意i∈sI与辅助变量x(c)i，并且是预先可知的；（2）总体单位水平。对于任意k∈s与辅助变量并且也是预先可知的。

接下来，本文将利用群水平和总体单位水平上的辅助信息来估计得到和当群校准权重wIi与总体单位的校准权重wk并不相关时，则此时群水平和总体单位水平上的约束信息可以表示为：

根据这些约束条件，可以得到群水平上相应的目标变量总值YI和总体单位水平上相应的目标变量总值Y的校准估计量。

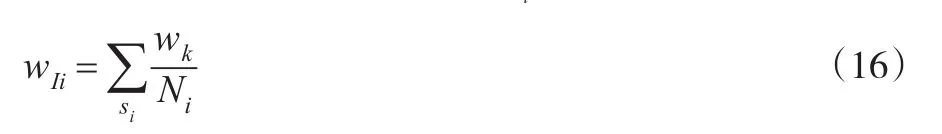
此时，新的校准约束可以表示为：

求解上式可以得出：

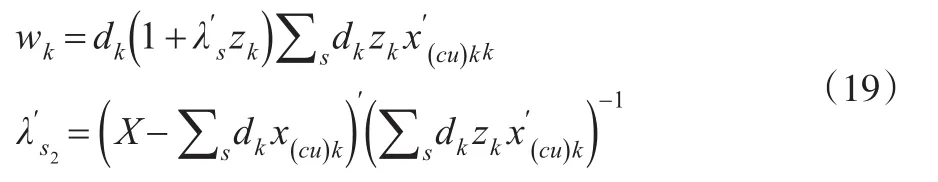
zk是有效的IV。

此时，可以得到相应的校准估计量：

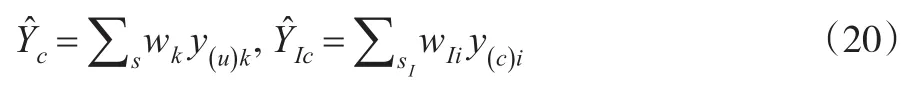
3 分析与结论

3．1 算例分析

对于我国而言，国有企业改革不断深化。以中央企业为例，截止2012年，中央企业的登记户数超过了21万户，其中混合所有制企业的登记户数超过6000户数，占登记企业总数28.5%以上。我国混合所有制企业的基本情况如表2所示。

表2 我国混合所有制企业的基本情况

本实验选取了我国混合所有制经济国有企业中进行了国企产权改革的企业为样本，共获得了1000家混合所有制国有企业。现有研究表明，国企产权改革会提升国企绩效（刘春、孙亮，2013；陈林、唐杨柳，2014）。为此，本文计算出了2008—2012年期间，这些国有企业的利润率提升（pr3）这一指标，用以衡量其绩效：

其中 pr3表示混合所有制经济中国企改革之后国企的绩效提升，用改革后3年的利润率提升（相对于改革前的最后一年）加权平均数来表示，rt表示第t的利润率提升水平。

通过上文所述的三种校准估计方法得到混合所有制国企产权改革的绩效数据，与实际的绩效数据进行比较，进而判断本文的抽样调查校准估计方法的有效性。

在模拟中，本文生成了一个独立同分布、样本量为1000的有效总体。由于模拟总体的真实值pr3是已知的，因此为了便于比较估计结果和真实值的差异，本文将用相对偏差（RB）和均方误差（MSE）来衡量：

3．2 研究结论

此时，本文可以得到这三种校准估计方法下国企业绩效改革的均方误差和相对偏差，见表3和表4。

表3 不同校准估计方法下混合所有制国企业改革绩效的均方误差

表4 不同校准估计方法下混合所有制国企业改革绩效的相对偏差

从表3和表4可以看出，在最短距离法、工具向量法和参数校准法这三种抽样调查校准估计法下，得到的均方误差都相差不大，但对于模拟中生成的5个总体，工具变量法得到的调整估计量要小于最短距离法得到的校准调整估计量，而参数校准法得到的调整估计量要小于工具变量法得到的调整估计量。对于相对偏差而言，三种的差距也不大：从绝对值的角度，工具变量法得到的调整估计量仍要小于最短距离法得到的校准调整估计量，而参数校准法得到的调整估计量同样要小于工具变量法得到的调整估计量。

[1]Estevao V M,Sarnda C E.A Functional Form Approach to Calibration [J].Journal of Official Statistics-Stockholm,2000,16(4).

[2]Estevao V M,Sarndal C E.Survey Estimates by Calibration on Com⁃plex Auxiliary Information[J].International Statistical Review,2006, 74(2).

[3]Harms T,Duchesne P.On Calibration Estimation for Quantiles[J].Sur⁃vey Methodology,2006,32(1).

[4]Rueda M,Sanchez-Borrego I,Arcos A.Model-Calibration Estimation of the Distribution Function Using Nonparametric Regression[J]. Metrika,2010,71(1)．

[5]Wu C,Sitter R R.A Model-Calibration Approach to Using Complete Auxiliary Information From Survey Data[J].Journal of the American Statistical Association[J].2001,96(453).

[6]刘建平等.辅助信息在抽样调查中的应用模型与方法[M].北京：中国统计出版社，2008.

[7]刘春,孙亮.政策性负担、市场化改革与国企部分民营化后的业绩滑坡[J].财经研究，2013,(1).

[8]陈林,唐杨柳.混合所有制改革与国有企业政策性负担——给予早期国有产权改革大数据的实证研究[J].经济学家，2014,(11).

[9]张明志,铁瑛,林娟.宏观经济学的经验研究方法：校准与估计之争[J].经济学动态，2014,(1).

（责任编辑/易永生）

C81

A

1002-6487（2016）24-0012-04

国家社会科学基金资助项目（14BGL038；13BGL054）

李国正（1986—），男，山东临沂人，博士，讲师，研究方向：公司治理。

张明玺（1986—），男，湖北武汉人，博士后，研究方向：消费金融。

谢艾香（1993—），女，湖北黄冈人，硕士研究生，研究方向：应用统计。