基尼系数理论最佳值的探讨与现实启示

2017-01-09冯玉广山西师范大学物理与信息工程学院山西临汾041004

统计与决策 2016年24期

郭军，冯玉广（山西师范大学物理与信息工程学院，山西临汾 041004）

基尼系数理论最佳值的探讨与现实启示

郭军，冯玉广
（山西师范大学物理与信息工程学院，山西临汾 041004）

文章以社会经济系统拟合类比热力学系统，通过探求玻尔兹曼系统的基尼系数达到探求社会经济系统基尼系数理论最佳值的目的。依据基尼系数的定义，直接利用玻尔兹曼统计的分布函数并借助Matlab软件，计算得到洛伦兹曲线和基尼系数，这一结果与现有讨论得到的值相当一致。

洛伦兹曲线；基尼系数；玻尔兹曼统计；收入分配；公平

0 引言

基尼系数是根据洛伦兹曲线定义的判断收入分配公平程度的指标，是国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标。其经济含义是：在全部居民收入中，用于进行不平均分配的那部分收入占总收入的比重[1]。关于基尼系数的定义及计算，首先需要说明的是洛伦兹曲线。洛伦茨曲线是用来反映社会收入分配或财产分配平等程度的曲线。由统计学家洛伦茨于1905年提出。洛伦兹把社会总人口按收入由低到高平均分为10个等级组，每个等级组均占10%的人口，再计算每个组的收入占总收入的比重。然后，以人口百分比为横轴，以收入百分比为纵轴，绘出一条实际收人分配曲线即洛伦茨曲线[2]。

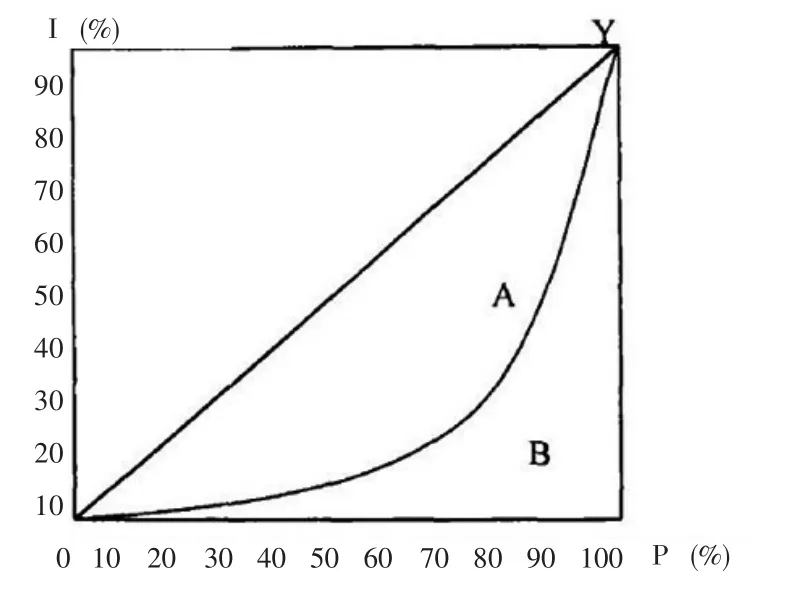
图1洛伦兹曲线图

图1中，OY表示绝对平均，等份的人数占有等份的收入或财产，OPY表示绝对不平均，社会财富全部集中在一个人。实际中的分配曲线介于二者之间，越接近于OY表示越平均，越接近于OPY表示越不平均。基尼根据洛伦兹曲线，计算出一个反映收入分配平等程度的指标，称为基尼系数。基尼系数是把洛伦茨曲线图中实际收入分配曲线与绝对平等线之间面积(用A表示)同这部分面积(A)加上实际收入分配曲线与绝对不平等曲线之间面积(用B表示)之和(A+B)相除，其商即为基尼系数。即：

基尼系数越小，表示越平均，反之则越不平均。

基尼系数的计算难在无法得到准确的洛伦兹曲线，所以通常的办法是依据大量的统计数据使用的五分法得到。有的学者以一些特殊的已知函数来拟合真实的洛伦兹曲线或分配函数，如多项式函数[3]、对数正态分布函数[4]广义χ2分布[5]等，从而计算基尼系数。大多数的文章是讨论基尼系数的理论计算及统计分析，很少有讨论基尼系数的理论最佳值。胡祖光（2004）最开始讨论了这个问题[6]，他指出：实践证明，收入分布平均或悬殊都不是最佳状态。收入悬殊的弊病人所共知，而收入平均不仅不利于效率，而且也不适应于生产与消费。那么，试问：某一时期的收入分布是否存在着一个理论最佳值呢？他假定收入分配服从简单的等差级数，后者收入比前者依次高出一个货币单位，当人口趋于无穷，也就是个人最高收入趋于无穷时，基尼系数趋于定值他认为这个值就是理论最佳值。洪兴建（2007）后来在假定收入分布为合意的橄榄型前提下计算出基尼系数的合意值也为并肯定了这一值的理论参考意义[7]。欧阳葵（2011）否定了认为这个值不仅不是最优值，而且是最差值，他指出胡祖光的假设太过特殊，洪兴建的收入分布类型太过经验性，缺乏理论基础[8]，但他并没有给出自己的最优值。本文需要说明的是，胡祖光的假设确实太过简单，太过理想，洪兴建的假定理论性不足。而且，在他们二人的讨论中，重在描述，给不出任何的现实意义和实际指导。事实上，基尼系数为的收入分布可以有很多种，陆善民（2006）在他的文章里指出，下面几条可能的洛伦兹曲线都能得到

所以，如果你说基尼系数g=1/3是理论最佳值，那首先要说清楚你给出的洛伦兹曲线为什么是最佳收入分配模式。

本文从另外一个方面考虑了这个问题，基于平衡态统计物理学中的玻尔兹曼统计。本文将洛伦兹曲线及基尼系数的概念引入到热力学平衡态中，以粒子数的累积比为人口累积比，以粒子的能量为人口获得的收入分配，以粒子的能量累积比为人口收入累积比。热力学平衡态并不是将系统的全部能量平均地分配给每一个粒子，这一点可以从麦克斯韦速度分布律看到。由此本文可以计算得到热力学平衡态系统的基尼系数近似于并以此类比社会经济系统，得出结论：社会经济系统的最佳基尼系数也是下面将计算出这一结果并讨论其带给我们的现实和理论思考，并且可以借用平衡态分布的物理意义来回答为什么这种分配模式就是最佳。

1 平衡态系统基尼系数的计算

统计物理学上给出玻尔兹曼系统的分布公式为[9]：

εl指第l能级的大小，ωl指第l能级的简并度，al指第l能级上的粒子数。上式必须满足两个平衡态约束条件：

需要说明的是：式（1）的导出是建立在平衡态统计物理的基本假设——等概率原理之上的，而正是这一假设对社会系统具有重要的启示和指导意义。

为了计算明了简单，本文做如下记号：

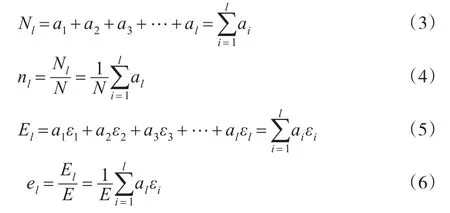
将al代入可得：

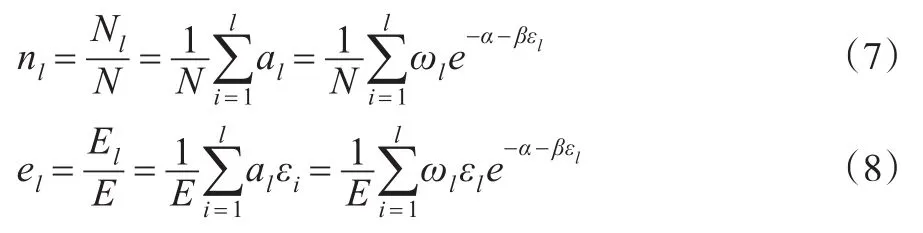
从上面两式可以得到如下公式：

下面先来计算nl，再根据上式得到el，由此便可描绘洛伦兹曲线，并计算基尼系数。在dxdydzdpixdpiydpiz范围内，分子可能的微观状态数为:

将上式代入公式可得:

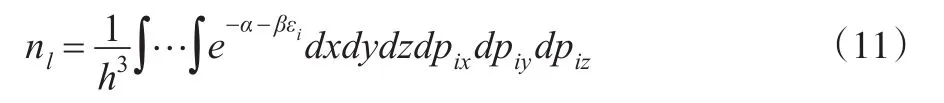
被积函数只是动量的函数，于是上式可写为:

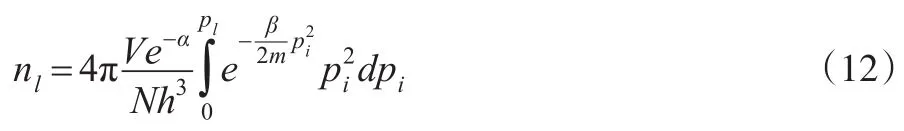
上式可以变换为如下形式:

只要求出后面的积分，则通过求导的方式可得到nl及el的表达式。这个积分是一个有限上下限的概率积分，被积函数的原函数不是初等函数，没有解析形式，但可以找到近似的函数来代替原函数[10,11]，王锦功(1981)和刘清珺等(2009)在各自的文章里提到了这一问题，本文在这里采用刘清珺等人给出的近似公式。令可将上式积分化为标准的概率积分，并利用近似公式可得：

于是nl的表达式如下：

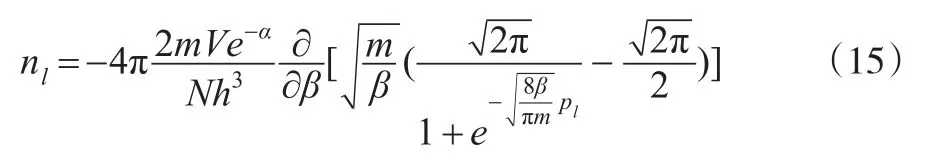
将偏导数求出，化简可得：

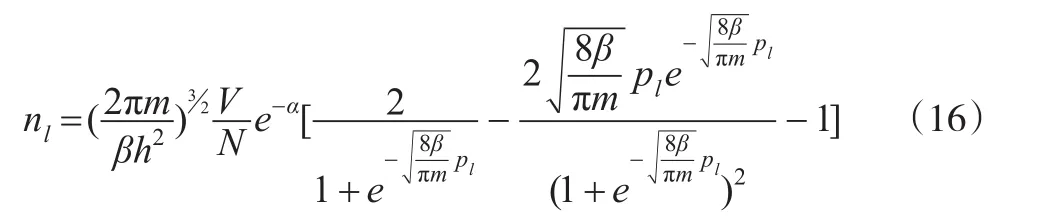
利用关系式（9），可得：

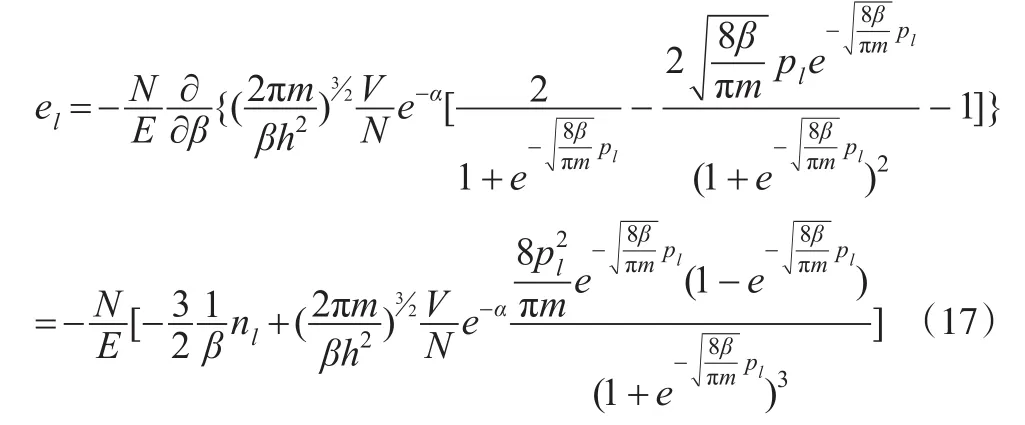
约束条件式（2）在统计物理学中表现为两个等式：

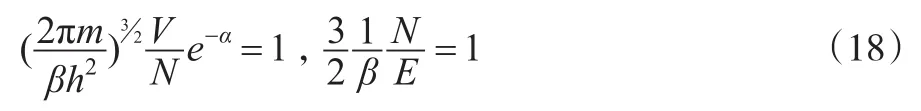
于是式（16）和式（17）化简为：

当 pl→∞，γ→∞，nl，el→1；当 pl→0，γ→0，nl，el→0，符合洛伦兹曲线的要求。

根据以上的关系式，并不能直接得到nl与el的关系式，但利用Matlab软件可以给出其相应的关系曲线。视γ为参数，图2描绘了nl，el与γ的函数曲线，其中实线表示nl与γ的关系，虚线表示el与γ的关系。图3即是根据参数关系式（21）和式（22）由Matlab软件给出的el与nl的函数关系曲线，即平衡态系统的洛伦兹曲线。

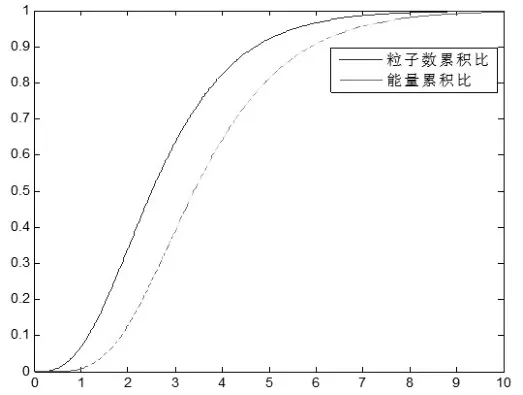
图2 nl，el与γ的函数曲线

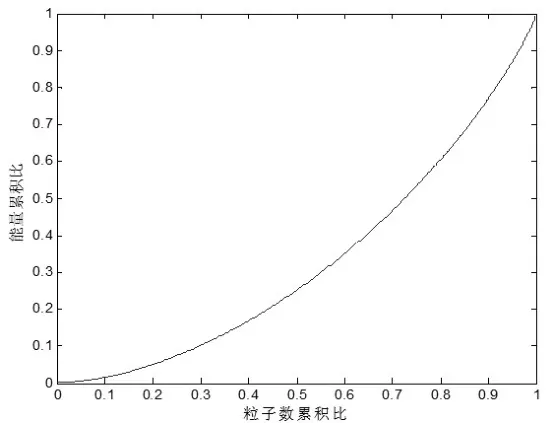
图 3el与nl的函数关系曲线

使用Matlab软件将nl20等分，可以找到其对应的el的值，见表1。如此可以用下面数据依据张建华给出的计算基尼系数的方法[12]来得到基尼系数。

表1 nl与el的20等分对照表

现在来计算基尼系数。按照国际上通用的五分法来计算，可得到基尼系数为：

用十等分和二十等分的数据得到的结果分别为：

用Matlab在图3的基础上，将nl10000等分，用插值法计算的结果为：

2 社会系统类比玻尔兹曼系统的几点说明

首先说明玻尔兹曼统计描述的系统的几个主要方面：

（1）系统由大量粒子组成，粒子数在1023数量级。

（2）系统处于平衡态，粒子数与能量不变。

（3）系统达到平衡态是通过自发的热运动。

（4）粒子之间通过碰撞传递能量，除此之外，别无其他相互作用。

（5）系统满足等概率原理和最概然分布。

等概率原理表明粒子与粒子之间是平权的，最概然分布是满足最大多数，基本上是全部状态出现的要求。

社会系统的几点说明：

（1）系统由全部人口组成，但国民收入分配不只以人为分配单位，收入的一部分给了地租，这一部分由土地的拥有者获得。

（2）在一定时间内，全部人口及全部国民收入基本稳定，不会出现跃变。

（3）系统的稳定，不仅表现在人的主观性上，还表现在国家的调控上，而且国家的控制对于稳定起到非常重要的作用。

（4）人与人之间的关系是相当复杂的，可以说，人的社会就是一个关系的社会，人与人之间的连带关系对于人的发展及收入分配有着决定性的作用。

（5）一般来说，除去特殊情况，人与人并不存在本质上的区别，无所谓天生的高与低，无论从生理上，还是智力上，人与人之间，除了“编号”，并没有什么不同。人一出生，从不曾就定下层级，定下能力，限制将来的所作所为。每个人都必须是平等的，每个人获得每种生活品质，得到任何一种分配报酬都是一样的可能性，就像玻尔兹曼系统的粒子，它们处在任何一个能级的概率都是一样的，在某个时间点是不公平的，但在全部时间内一定是平均的。

关于两个系统的共性，做一些类比，改变人类系统不同与自然系统的特点，可以将二者统一对待，自然系统的最佳基尼系数就是人类系统的最佳基尼系数，这也就是本文的目的。

（1）国民总收入类比于系统总能量。

（2）个人和土地类比于粒子，粒子是能量的载体，个人和土地是收入的载体，土地的收入会归在个人身上，但土地的归属可变，每个人拥有任何一块土地都是一样的可能性。

（3）个人按收入的分布类比于玻尔兹曼分布。本文认同人与人是平等的，每个人处在每一种生活状态的概率都是一样的，即已是类比了等概率原理和最概然分布。

虽然已经做了类比，但还有几个方面需要说明。在上文指出，社会系统与自然有很大不同，这些不同从根本上区别了社会系统与自然系统。自然系统是我们无法改变的，自然原理就是存在法则，自然规律就是自然界的宪法，任何存在都不可能违背该宪法，自然的存在就是对自然宪法最好的适应。既然平衡态系统是自然规律要求下达到的最终的状态，它无疑就是最佳的状态，这也是上文算出的基尼系数就是最佳值的原因。那么，如何改变社会系统，以使其达到最佳状态呢？参照前面给出的不同，本文提出如下几点意见：

（1）保证人与人之间的平等。这里主要包括两个方面的平等：第一，出生的平等，包括人的出生不带着先天的缺陷，人权上的平等，社会和政治上的平等。第二，发展的平等，包括成长环境的平等、教育的平等、公共资源分配的平等。

（2）国家宪法，这是类比于自然宪法而言的。个人在社会的合理存在必须遵从宪法原则，违背自然规律的现象是不可能存在的。前提是国家宪法必须合理有效。

（3）人与人之间的关系是最大的不同，这点似乎不可能克服。消除或者降低人与人的连带关系，也就是使个人的主观性在某个事态中不能起主要作用，那么，一切依照准则、规章、法律和制度，则能强调法律的作用，弱化人的干预。

3 结论

本文基于玻尔兹曼系统求得其基尼系数，并以社会系统拟合热力学系统，探求收入分配的理论最佳。本文得到这个值近似于在数值上，这与胡祖光和洪兴建给出的值一致。但他们并没有将问题说清楚。主要有以下几个方面：（1）为什么这个值是最佳值。（2）相应的分布也即洛伦兹曲线是如何的。（3）这样的分布在现实中的意义。（4）政府应该怎么做。下面来回答这几个问题。第一，平衡态是热力学系统发展的最终状态，它是在最大限度满足各种状态的出现的前提下实现的，等概率原理的假设完全满足了粒子与粒子之间的平等要求，这种平衡态是系统发展的理想状态，它所对应的基尼系数就是最佳值。社会系统不同于热力学系统，但热力学系统可视为社会系统一种简化的、理想的模型，因此热力学平衡态对社会系统具有一定的参考和指导价值，所以说是社会系统基尼系数的理论最佳值。第二，同一收入水平的人群数量与收入量的关系应满足玻尔兹曼分布函数，即式（1）。相应的洛伦兹曲线如图3所示。第三，该分布是在一定约束条件下的最概然分布，该分布表示在整体上，在人人平等的前提下，最大限度实现了公平。这也是玻尔兹曼系统带给我们的启示：真正的公平，决不是收入上的绝对平均，更不可能是收入上的绝对不平均，人与人的收入在本质上就一定会存在一定阶梯。那么什么才是真正的公平？玻尔兹曼系统告诉我们，本质上的公平就是粒子与粒子之间属性的相同，它们之间除了可区分的“编号”，都是一样的，都是平等的。也就是说，社会的公平，本质上在于人与人属性的相同，在生理、智力、环境、政治上，除了个人的“编号”，人与人都是一样。那么，这也就为国家更好地成为人民的保护伞提供了指导方向。第四，国家的存在，就是要尽可能的保证和促使人与人之间达到属性上的一致，身体上都是一样的健康，也就是医疗配置上的合理；智力上一样的发达，即教育资源上公平，本文认为这个最为关键，个人在意识上认同了人与人的平等，那么就能更好地发挥人的主动性，更好地认识、接受和适应本质上收入不平均的社会状态，更好地追求一切皆平等概率的社会生活可能。不存在怎样的主宰者赋予一些人高质量高收入的权利，也不存在一些人就应该长久待在社会最底层的限制。就业上一样的待遇，没有连带关系，没有主观差异；政治上享受同等的权利和尽责同等的义务。

[1]逄锦聚，洪银兴，林岗，刘伟等.政治经济学（第二版）[M].北京：高等教育出版社，2003．

[2]龚红娥.基尼系数及其实际应用[J].市场与人口分析，2002，8(6)．

[3]庄健，张永光.基尼系数和中等收入群体比重的关联性分析[J].数量经济技术经济研究，2007，(4).

[4]成邦文.基于对数正态分布的洛伦兹曲线与基尼系数[J].数量经济技术经济研究，2005，(2).

[5]张顺，郝卉，韩书平，林道荣.基于广义χ2分布的洛伦兹曲线简洁模型[J].数学的实践与认识，2015，45(3)．

[6]胡祖光.基尼系数理论最佳值及其简易计算公式研究[J].经济研究，2004，(9)．

[7]洪兴建.基尼系数合意值和警戒线的探讨[J].统计研究，2007，24(8)．

[8]欧阳葵.理论基尼系数及其社会福利含义的讨论[J].统计研究，2011，28(5)．

[9]汪志诚.热力学统计物理（第四版）[M].北京：高等教育出版社，2008．

[10]王锦功.概率积分在整个区间上的近似公式[J].吉林大学自然科学学报，1981，(4)．

[11]刘清珺，陈婷，陈舜琮，刘清.正态分布近似计算公式及其在实验结果中的应用[J].现代测量与实验室管理,2009，(9)．

[12]张建华.一种简便易用的基尼系数计算方法[J].山西农业大学学报（社会科学版）,2007，6(3)．