热力参数的KPCA-RBF网络建模及传感器故障诊断方法*

李鸿坤， 陈坚红，2， 盛德仁，2， 李 蔚，2

(1.浙江大学热工与动力系统研究所 杭州，310027) (2.浙江省制冷与低温技术重点实验室 杭州，310027)



热力参数的KPCA-RBF网络建模及传感器故障诊断方法*

李鸿坤1， 陈坚红1，2， 盛德仁1，2， 李 蔚1，2

(1.浙江大学热工与动力系统研究所 杭州，310027) (2.浙江省制冷与低温技术重点实验室 杭州，310027)

针对复杂恶劣环境下机组热力参数的数据监测及传感器故障诊断问题，建立了融合机理分析、核主元分析(kernel principle component analysis，简称KPCA)与径向基神经网络(radial basis function，简称RBF)的发电机组热力参数预测及传感器故障检测模型。首先，根据机理分析得到完备的辅助变量集，并利用核主元分析提取辅助变量的特征信息以有效处理发电机组中高维、强耦合的非线性数据；其次，将主元变量集输入径向基神经网络进行学习，实现热力参数的重构；最后，基于预测模型与窗口移动法实现传感器的故障诊断，并对故障数据进行及时修复和准确替换。以燃气轮机排气温度为例进行验证的结果表明，该预测模型具有更高的精度和泛化能力，能在传感器故障发生初期及时发现并识别故障类型，检测效果优良。

机理分析； 核主元分析； 径向基神经网络； 预测建模； 传感器故障诊断

引 言

传感器故障检测方法主要分为三大类：基于数据驱动、基于解析模型和基于知识的方法[1]。国内外学者对传感器故障诊断方法进行了大量的研究。单一的诊断方法有关联规则分类算法[2]、基于观测器方法[3]、神经网络方法[4-5]、支持向量机(support vector machine，简称SVM)[6-7]和专家方法[8]等。另外，许多混合的检测方法也被应用到实际中，取得了很好的效果[9-10]。Zhang等[11]提出利用主元分析法(principal component analysis，简称PCA)提取主元，通过自组织映射神经网络进行预测建模的传感器诊断方法。该方法被广泛应用于预测建模和复杂工业过程的故障诊断[12-14]。相比PCA，KPCA方法特征信息提取速度快、保留充分，是较多学者将KPCA应用于建模和诊断的主要原因[15]。然而，很多文献只是提出识别故障的方法，却没有考虑实际过程中数据修复和替代的准确性问题。基于预测模型的诊断方法不仅可以实时诊断，还可以对故障数据进行准确地替换。鉴于此，笔者提出基于预测模型的传感器故障检测和数据修复方法。

该方法通过机理分析得到与测量信号存在依赖关系的所有辅助变量，然后利用KPCA方法有效地提取辅助参数的高阶非线性特征，降低数据维数，消除数据的冗余与噪声。将经过特征值提取后的主元变量集作为RBF神经网络的输入，得到预测值后通过数据统计特征，以窗口移动法实现传感器的故障检测和故障数据的及时准确替换，保证热力系统运行的安全可靠。

1 发电机组运行参数预测模型

1.1 核主成分分析

发电机组热力参数具有非线性、强耦合、维数高等特点，对模型的精度产生较大的影响。通过KPCA的非线性映射去除数据冗余、减少噪声及降低数据维数的目的[14]。

(1)

(2)

1.2 RBF神经网络

RBF神经网络是个3层的前馈神经网络，其具有收敛速度快、不易陷入局部极小点、鲁棒性好和易于实现等优点，且可以在任意精度下逼近任意的非线性函数。笔者选择高斯函数作为径向基函数，则RBF网络的输出可以表示为

(3)

RBF网络具体的学习过程可参考文献[16]。影响RBF网络性能的主要为基函数中心ci、宽度系数σi和输出层权值wij。在设计时要选取合适的参数和数据预处理方法，以保证网络回归性能最优。

1.3 运行参数间依赖关系机理分析

运行参数建模需要选取与它存在依赖关系的辅助变量，而机理分析是其中非常关键的一步。笔者采用综合机理分析方法来确定与待建模参数相关的辅助变量以保证模型的合理性。通过质量守恒、能量守恒原理、机组运行机制、机组控制系统及工艺流程来分析相关的辅助变量。这样得到的相关变量组是预测建模的基础。完备的相关变量组可有效降低建模误差，提高模型的精度。

1.4 模型结构及参数选取

准确的模型是传感器故障诊断的关键，KPCA-RBF预测模型的建模思路是：首先，利用机理分析方法得到与建模参数存在依赖关系的且是完备的辅助变量；其次，利用KPCA方法提取数据的非线性特征信息；最后，将经过特征值提取后的高维空间主元变量集输入至RBF神经网络进行学习和重构。KPCA-RBF预测模型的实现结构如图1所示，其中箭头表示数据流向，虚线表示训练数据流，实线表示测试数据流。

图1 KPCA-RBF方法建模流程图Fig.1 Modeling flow chart of KPCA-RBF method

建模过程中，对训练数据及对应的输出值进行零均值归一化，并采用基于最大熵原则的非高斯性测度理论[17]对KPCA的核参数σk与CPV阈值E进行优化，选择合适的RBF学习算法确定RBF参数，最后采用测试数据测试模型的精度和泛化能力。

2 传感器故障诊断

笔者将基于KPCA-RBF预测模型得到的参数预测数据作为真实参照值，通过模型生成的残差对故障进行识别和分离。将模型参数保存于机组的实时数据库中，实现实时预测与诊断。诊断过程主要涉及的评价指标为：模型预测值及其均值和标准差、传感器实测值及其均值和标准差、残差及其均值和标准差及每个数据的相对误差等。

由于测量过程中各种噪声因素的干扰以及模型本身存在的误差影响，使得无故障状态下残差不为零，因而需要确定合理的阈值来判断是否发生了故障。笔者提出窗口移动法来检测和识别传感器故障类型。窗口移动法及判别步骤如下。

1) 设定L，M和N，设定阈值T0～T6。

3 实例分析

3.1 模型辅助变量选取

笔者以西门子V94.3A型燃气轮机排气温度为例来验证该建模方法。燃气轮机排气温度是判断燃气轮机运行状态的一个重要运行参数，如排气温度测量不准，将影响到透平进口温度的控制。通常会使用高精度的热电偶，并定期对燃气轮机排气温度测量系统进行准确性校验[19]。因此，建立燃气轮机排气温度的预测模型，对燃气轮机排气温度传感器进行监测，这对于机组的运行可靠性和安全性是非常重要的。

对于燃气轮机的排气温度，从能量守恒、质量守恒原理、机组工艺流程及传感器参数测量方法等角度进行综合机理分析，获取对其产生影响的辅助变量。分析可得相关参数为进入系统的天然气及压气机的压力、温度、流量；与燃机相关的转速、燃机排气压力、烟气流量等。此外，影响燃料进气量的预混控制阀阀位、值班控制阀阀位、扩散控制阀阀位(机组正常运行时为全关，建模时不考虑)、天然气危急遮断阀(emergency stop valve，简称ESV)阀后压力、天然气流量、进口导叶(inlet guide vane，简称IGV)的开度等参数也是影响燃机透平出口温度的重要因素。从燃机排气温度控制框图获知温度控制基准主要引入的修正参数有压气机排气温度、压气机排气压力、注水流量及燃机负荷等。

根据以上分析，选取表1所示的12个变量为燃气轮机排气温度模型的辅助变量。

表1 燃气轮机排气温度预测模型辅助变量

Tab.1 Auxiliary variables for model of gas turbine outlet temperature

编号变量名称编号变量名称1燃机功率7天然气ESV阀后压力2燃机转速8天然气ESV阀前温度3压气机出口压力9机组天然气体积流量4压气机出口温度10燃机IGV开度位置5预混控制阀阀位11燃气轮机排气压力6值班控制阀阀位12燃烧室注水(蒸汽)量

训练样本的选取是影响模型性能的重要因素。所以选取的样本要分布均匀，具有广泛的代表性，是各工况下的典型数据，以使所建模型泛化性能较好。笔者选取的训练样本覆盖了春、夏、秋、冬，温度从-5℃～35℃，大气压力从99 kPa～104 kPa，功率从30%～100%基本负荷之间的共250组典型运行工况数据。

3.2 KPCA-RBF模型的参数选取

KPCA方法的实质是将数据变换到一个更合适的空间，即特征空间，然后在这个空间中做PCA特征提取。PCA的前提约束是输入空间中的数据呈高斯分布，所以对KPCA来讲，最优的核函数形式及参数应使映射数据在特征空间中的分布尽量逼近高斯分布。基于此，笔者结合文献[17]，采用基于最大熵原则的多维变量非高斯性测度的KPCA核参数选取方法。

评价特征空间F中前P个主分量高斯分布的逼近程度，非高斯性测度定义及计算方法为

(4)

(5)

另外，合适的主元个数也是影响模型精度的重要因素。如图2所示，当阈值E不变时，随着核参数σk的增大，主元个数逐渐减少，当σk大于一定值后，主元个数保持不变，表明在大部分情况下主元个数主要取决于E。通过计算表明，特征子空间的整体非高斯性测度先增加后减小，当核参数σk>6时，非高斯性测度趋近于零，即较大的核参数使得KPCA的特征提取具有较好的性能。综合考虑主元个数及特征子空间的整体非高斯性测度，笔者选择CPV阈值E=90，核参数σk=18.7。此时的主元个数为5。5个主元的贡献率见图3，贡献率总和为92.56%。

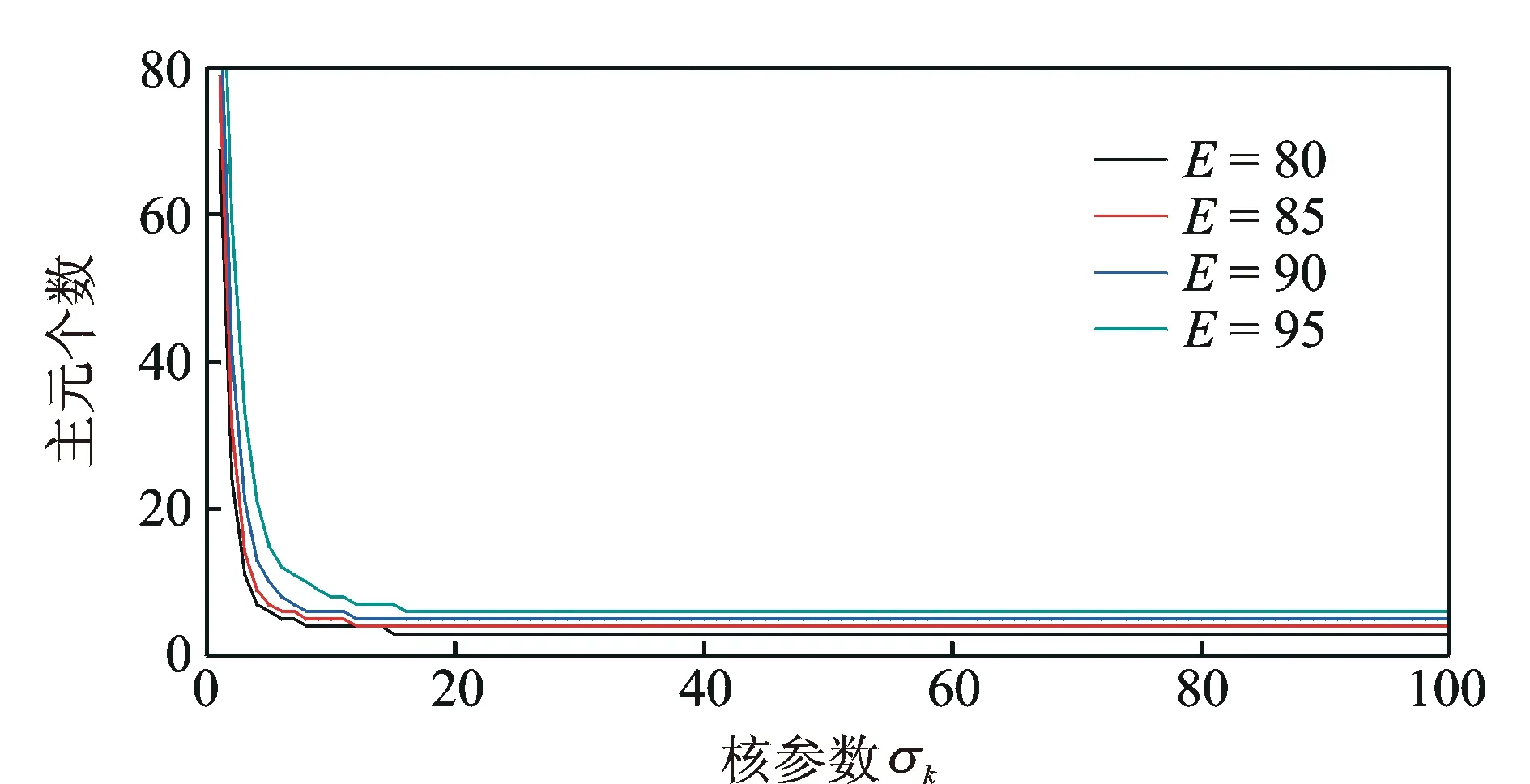
图2 主元个数随核参数σk的变化趋势图Fig.2 Variation tendency of the number of principal components along with σk

图3 模型主元的累积方差贡献率Fig.3 Cumulative percent of variance of pivot elements

将5个主元作为RBF神经网络的输入，构建燃气轮机排气温度传感器的预测模型。RBF网络采用自组织学习算法，通过K-均值聚类方法求取基函数中心ci，并确定高斯函数方差σi，根据最小二乘法确定隐含层到输出层之间的权值wij。综合KPCA和RBF的参数选择，按照以上参数建立基于KPCA-RBF的燃气轮机排气温度预测模型。

3.3 KPCA-RBF模型误差分析

为了测试模型的性能，选取250组各种运行工况作为训练样本，采用KPCA方法按照寻优后得到的主元个数作为RBF网络的输入，完成建模。另外选取200组数据作为测试样本检验模型。作为对比，用 RBF网络及PCA-RBF网络对相同数据建立燃气轮机排气温度软测量模型，相关结果见表2，KPCA-RBF模型的实际值与预测值对比见图4。

表2 各模型预测误差的比较

Tab.2 Forecasting errors of different models

模型RBFPCA⁃RBFKPCA⁃RBF平均相对误差/%0．74410．53200．1852

图4 KPCA-RBF模型预测值与真实值对比图Fig.4 Comparison between measured value and predicted value of KPCA-RBF model

由表2和图4的对比可以发现，对于同样的训练样本和测试样本，用RBF模型的预测误差比用PCA-RBF模型和KPCA- RBF模型的预测误差要大得多，这是因为RBF网络算法本身泛化能力较差，容易产生过拟合所导致的。由于采用了非线性的KPCA方法选取输入变量的独立主元，使 KPCA-RBF模型具有最小的预测误差，表明KPCA-RBF具有良好的预测效果。

3.4 传感器故障检测仿真及结果分析

以燃气轮机排气温度传感器为例，按照式(6)和表3[20]的规则仿真出4种传感器故障类型，其中yf为传感器故障仿真数据，ym为传感器正常工作状态下的真实值(取自电厂的实时数据库)，fk按照表3规则来选取，ξ为调整系数。按照第2节诊断规则在VS2010环境下编制程序，对各种故障进行检测和识别。由于KPCA-RBF模型的预测精度基本小于0.5%，所以将故障检测阈值T0设为0.005。综合考虑诊断程序的漏检率、误诊率及稳定性等实际因素，设定特征长度M为4，窗口长度N为25，窗口移动步长L为10。设定T1～T6如表4所示，预测及诊断结果如图5所示。

(6)

表3 传感器故障仿真算法

Tab.3 Expression for four types of sensor faults

故障类型表达式精度下降Efk()=0，Ef2k()=δ2f=δ2完全故障fk+ym，k/ξ=δ漂移故障fk=fk-1-δ，f0=δ恒定偏差fk=fk-1，f0=δ

针对以上4种故障类型，由检测诊断程序仿真结果表明，各加载故障发生时，程序检测的故障发生位置准确，故障类型判断准确。当诊断传感器故障时，彻底失效和精度下降故障需要一个窗口即可识别，漂移故障和恒定偏差需要窗口移动一次来识别。由于漂移故障初始阶段误差小于T0，所以识别漂移故障稍微滞后，但故障前期数据的极小偏差不影响机组的正常运行，因此也可以在故障发生初始阶段完成识别。实验结果表明，利用该方法进行传感器的故障诊断是切实可行的。

表4 燃机排气温度传感器诊断阈值设定

Tab.4 Thresholds of diagnostic procedure for compressor outlet temperature sensor

符号T0T1T2T3T4T5T6阈值0．0053．00．50．10．11．151．45

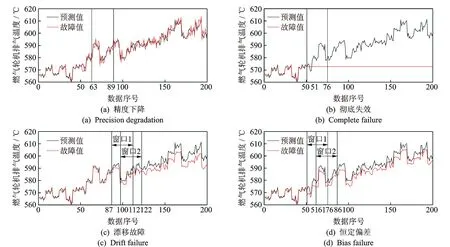
图5 4类传感器故障诊断仿真结果Fig.5 Four types of sensor fault diagnosis simulation results

4 结束语

笔者建立了融合机理分析、核主元分析与径向基神经网络的发电机组热力参数预测和传感器故障检测模型。利用机理分析得到完备的辅助变量，采用KPCA提取数据的非线性特征信息，消除变量之间的冗余，将经过特征值提取后的高维空间主元变量集输入至RBF神经网络进行学习和重构。基于该模型实现了对传感器的故障检测，并可以及时以精确的数据替换故障数据，保证热力系统的安全运行。以燃气轮机排气温度为例对预测模型及诊断方法进行了验证，结果表明其应用效果优良。该方法融合机理分析和数据驱动方法，适用于发电机组等复杂的工业过程运行参数建模，具有精度高、泛化能力强等特点。基于该模型与窗口移动法的传感器故障诊断具有高时效性、高准确性及工程可实现性强等优点，并能对故障数据实现及时修复和准确替换。

[1] Isermann R. Model-based fault-detection and diagnosis-status and applications[J]. Annual Reviews in Control, 2005, 29(1): 71-85.

[2] 鲍文，于达仁，王伟，等. 基于关联规则的火电厂传感器故障检测[J]. 中国电机工程学报, 2004, 23(12): 170-174.

Bao Wen, Yu Daren, Wang Wei, et al. Sensor fault detection in thermal power plants based on association rule[J]. Proceedings of the CSEE, 2004, 23(12): 170-174. (in Chinese)

[3] Li Zhenhai, Jaimoukha I M. Observer-based fault detection and isolation filter design for linear time-invariant systems[J]. International Journal of Control, 2009, 82(1): 171-182.

[4] Fast M, Palme T. Application of artificial neural networks to the condition monitoring and diagnosis of a combined heat and power plant[J]. Energy, 2010, 35(2): 1114-1120.

[5] Palmé T, Fast M, Thern M. Gas turbine sensor validation through classification with artificial neural networks[J]. Applied Energy, 2011, 88(11): 3898-3904.

[6] Sheibat-Othman N, Laouti N, Valour J P, et al. Support vector machines combined to observers for fault diagnosis in chemical reactors[J]. The Canadian Journal of Chemical Engineering, 2014, 92(4): 685-695.

[7] 万书亭,佟海侠,董炳辉. 基于最小二乘支持向量机的滚动轴承故障诊断[J]. 振动、测试与诊断,2010,30(2):149-152.

Wan Shuting, Tong Haixia, Dong Binghui. Bearing fault diagnosis using wavelet packet transform and least square support vector machines[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(2):149-152. (in Chinese)

[8] Wu Jianda, Liu Chiuhong. An expert system for fault diagnosis in internal combustion engines using wavelet packet transform and neural network[J]. Expert Systems with Applications, 2009, 36(3): 4278-4286.

[9] 林海军，滕召胜，迟海,等.基于信息融合的汽车衡称重传感器故障诊断[J].控制理论与应用，2010，27(1)：25-30.

Lin Haijun, Teng Zhaosheng, Chi Hai, et al. Diagnosis for load cells in truck scale based on information fusion[J]. Control Theory & Applications, 2010，27(1)：25-30. (in Chinese)

[10]冯志刚,王祁,Shida K. 基于EMD和SVM的传感器故障诊断方法[J]. 哈尔滨工业大学学报,2009(5):59-63.

Feng Zhigang, Wang Qi, Shida K. Sensor fault diagnosis based on empirical mode decomposition and support vector machines[J]. Journal of Harbin Institute of Technology, 2009,(5):59-63. (in Chinese)

[11]Zhang Yu, Bingham C, Gallimore M, et al. Applied sensor fault detection, identification and data reconstruction based on PCA and SOMNN for industrial systems[C]∥Proceedings of the 12th WSEAS International Conference on Applications of Electrical Engineering (AEE′13). Cambridge, USA: WSEAS,2013:38-43.

[12]Xu Ping, Wang Youcai, Wang Kai, et al. Fault detection and diagnosis for sensor in complex control system based on KPCA[J].Applied Mechanics and Materials, 2014, 623: 202-210.

[13]胡金海,谢寿生,侯胜利,等. 核函数主元分析及其在故障特征提取中的应用[J]. 振动、测试与诊断,2007,27(1):48-52.

Hu Jinhai, Xie Shousheng, Hou Shengli, et al. Kernel principal component analysis and its application to fault feature extraction[J]. Journal of Vibration, Measurement & Diagnosis, 2007,27(1):48-52. (in Chinese)

[14]Xu Tao. Sensor fault detection and identification method with KPCA in the process of aero-engine ground testing[J]. Applied Mechanics and Materials, 2013, 303: 297-301.

[15]Jia F, Martin E B, Morris A J. Non-linear principal components analysis with application to process fault detection[J]. International Journal of Systems Science, 2000, 31(11): 1473-1487.

[16]杨帆, 张玉杰, 张彩丽. 基于 PCA 和 RBF 网络的故障诊断技术及其应用研究[J]. 计算机测量与控制, 2008, 16(7): 903-905.

Yang Fan, Zhang Yujie, Zhang Caili. Research on PCA and RBF neural network based fault diagnosis technology and its application[J]. Computer Measurement & Control, 2008, 16(7): 903-905. (in Chinese)

[17]王毅娜. 基于非高斯估计的Kernel PCA核优化方法及应用[D].西安：西安电子科技大学,2006.

[18]Allano L, Dorizzi B, Garcia-Salicetti S. Tuning cost and performance in multi-biometric systems: a novel and consistent view of fusion strategies based on the sequential probability ratio test (SPRT)[J]. Pattern Recognition Letters, 2010, 31(9): 884-890.

[19]杨瑜文. 燃气轮机发电机组功率与排气温度控制[J]. 燃气轮机技术, 1998, 11(2): 26-28.

Yang Yuwen. Power of gas turbine generator unit under the control of exhaust gas temperature[J]. Gas Turbine Technology, 1998, 11(2): 26-28. (in Chinese)

[20]Dunia R, Qin S J, Edgar T F, et al. Identification of faulty sensors using principal component analysis[J]. AIChE Journal, 1996, 42(10): 2797-2812.

10.16450/j.cnki.issn.1004-6801.2016.06.002

*浙江省自然科学基金资助项目(LY13E060001)

2014-11-13；

2015-01-31

TK39； TH811

李鸿坤，男，1991年9月生，硕士生。主要研究方向为电厂故障诊断和热力系统优化。曾发表《The improved distribution method of negentropy and performance evaluation of CCPPs based on the structure theory of thermoeconomics》(《Applied Thermal Engineering》2006, Vol.96)等论文。 E-mail：lhk@zju.edu.cn

陈坚红，男，1967年1月生，博士、副教授。主要研究方向为电厂热力系统分析和热工自动化技术。 E-mail：power@zju.edu.cn