ARIMA模型在成都市成华区狂犬病暴露监测数据分析中的应用
2017-01-09杨静张强
杨 静 张 强
ARIMA模型在成都市成华区狂犬病暴露监测数据分析中的应用
杨 静1,2张 强1△
目的了解成都市成华区狂犬病暴露监测数据的基本情况和特征;利用狂犬病暴露数据建立ARIMA模型,对2016年狂犬病暴露数据进行预测,为人用狂犬病疫苗、免疫球蛋白需求计划,犬伤处置报销费用预算的制定提供参考依据。方法应用SPSS19.0对成都市成华区2009-2014年逐月狂犬病暴露数据构建ARIMA模型,以2015年狂犬病暴露数据为验证样本,验证模型的预测效果,并预测2016年逐月狂犬病暴露数据。结果最优模型ARIMA(1,0,0)(1,1,0)12能较好地拟合既往时间段的狂犬病暴露数据序列,拟合值与实际值基本保持一致的曲线趋势。2015年1月-12月检验样本的预测结果显示,暴露实际值均在预测可信区间内,均方根误差为28.79,平均绝对误差为82.36,平均绝对误差百分比为9.08%。结论ARIMA(1,0,0)(1,1,0)12模型能较好地拟合成都市成华区狂犬病暴露数变动趋势,适用于狂犬病暴露人数的预测。
狂犬病 ARIMA模型 预测
狂犬病是由狂犬病毒引起的一种侵犯中枢神经系统为主的急性人兽共患传染病。王梅、周航等人[1]的研究显示,狂犬病的发病具有明显的季节性,发病高峰在夏、秋季。开展狂犬病暴露监测数据的分析应用,是合理制定疫苗需求计划、犬伤处置费用报销政策等狂犬病防控措施的有力保障。ARIMA模型是时间序列分析中较为成熟和应用较为广泛的方法之一,通过差分对序列线性趋势、周期性等确定性信息进行提取,具有充分利用历史观测值,短期预测效果较好的优势。本文利用成都市成华区2009-2015年狂犬病暴露监测月报表数据构建ARIMA模型,预测2016年逐月狂犬病暴露数,为该区2016年人用狂犬病疫苗、免疫球蛋白的需求计划和犬伤处置报销费用预算的制定提供参考依据。
资料与方法
1.资料来源
数据来源于2009-2015年成华区各家犬伤门诊的《成都市成华区犬伤门诊月报表》。
2.ARIMA模型建模过程
(1)时间变量的定义与序列平稳化 将2009年1月-2015年12月成华区犬伤月报表数据序列的时间单位定义为年份、季度、月份型。通过时间序列图观察序列的平稳性,对不平稳的序列进行数据转化、差分处理,使其成为零均数的平稳时间序列,达到以下要求[2]:均数不随时间变化;方差不随时间变化;自相关系数与所在的时间点无关,仅与时间间隔距离有关。
(2)模型识别和定阶 自回归移动平均模型ARIMA(p,d,q),可以写成Φ(B)wt=θ(B)ut,其中wt为zt的d阶差分;ut为随机剩余项(又称为白噪声),p是自回归的阶数,d指差分的次数,q是移动平均的阶数。包含季节趋势的时间序列可通过ARIMA(p,d,q)(P,D,Q)s过程来拟合,其中P,D,Q,s分别是季节性自回归阶数、季节差分次数、季节性移动平均阶数、季节周期。定阶即利用自相关图(ACF)、偏自相关图(PACF)和互相关图(CCF)确定p、d、q等参数的过程,首先根据ACF、PACF图形的截尾或拖尾情况进行模型的初步拟合,再根据拟合的结果进行相应调整、不断修正,并结合评价指标由低阶向高阶选择模型的办法确定模型的p、d和q。
(3)参数的估计 依据BIC确定模型的阶数,采用最小二乘法估计出p个自回归参数φ1、φ2…φp,q个移动平均参数θ1、θ2…θq,P个季节自回归参数Ф1、Ф2…ФP,以及Q个季节移动平均参数
(4)模型的检验与优化 根据平稳的R方、正态化的BIC准则判断模型的拟合优度(BIC值相对较小的模型较好)。由Ljung-BoxQ检验结果对模型残差序列进行白噪声检验,判断所建模型的适合性。在所有通过检验的模型中,确定标准化的BIC值较小,模型较为简洁的为最优模型[4]。
(5)模型的验证和预测 以2015年1-12月犬伤暴露数据为验证样本,采用均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)作为评价指标,通过比较预测值和真实值来评价模型的预测精度。选用较优模型对2016年狂犬病逐月暴露数进行预测。
3.统计软件处理
利用SPSS 19.0统计软件建立ARIMA模型,P<0.05表示差异有统计学意义。
结 果
1.成华区狂犬病暴露监测数据基本情况
成都市成华区2009-2015年狂犬病暴露逐月监测数呈现明显的季节性波动,每年从1月开始呈逐月上升趋势,至7、8月份达到峰值,之后逐月下降。2009-2015年的狂犬病暴露数最低为8441例,最高为10285例,年平均数为9023例,年暴露监测数基本围绕该平均值波动。
2.序列的平稳化
观察原始序列自相关图发现序列有周期性变化规律,周期为12个月。原始偏自回归函数在k=1后呈现余弦衰减波形。因此,需对原始序列进行一次季节性差分,观察差分后的自相关和偏相关分析图,可见,其自相关函数在k=1后呈现衰减趋势,仅当k=1和k=12时,自回归系数明显突破了可信区间界值,其偏自回归函数在k=1后呈现逐渐衰减至零的趋势,并落入可信区间,此时的时间序列已基本趋于平稳,见图1。
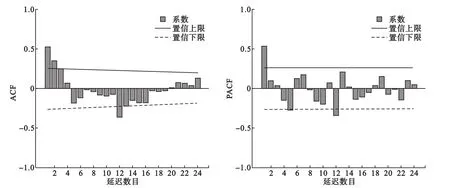
图1 成都市成华区狂犬病暴露监测数一阶季节差分自相关和偏相关分布图
3.模型的识别和定阶
由于成都市成华区2009年1月-2014年12月狂犬病暴露数序列存在明显的季节性趋势,季节性周期为12个月,故选用ARIMA(p,d,q)(P,D,Q)S过程来拟合建模。对序列进行了1次季节性差分,因此确定d=0,D=1。根据一阶季节差分的ACF图,k=1后函数呈现衰减趋势,只有k=1、k=2和k=12时,自回归系数突破了可信区间界值,可以选择q=1或2,Q=1。根据一阶季节差分的PACF图,k=1后函数呈现衰减趋势,可以选择p=1,P=1。因此可以选出5组模型,ARIMA(1,0,1)(1,1,1)12、ARIMA(1,0,0)(1,1,1)12、ARIMA(1,0,0)(1,1,0)12、ARIMA(2,0,1)(1,1,1)12、ARIMA(2,0,0)(1,1,0)12。
4.模型参数估计
模型ARIMA(1,0,0)(1,1,0)12的标准化BIC值=9.304,在拟合的所有模型中最小;模型拟合效果度量Ljung-Box Q差异无统计学意义(Q=22.076,P=0.141),模型的残差为白噪声;且模型中的参数检验均有意义,见表1,说明所拟合模型是有效的。
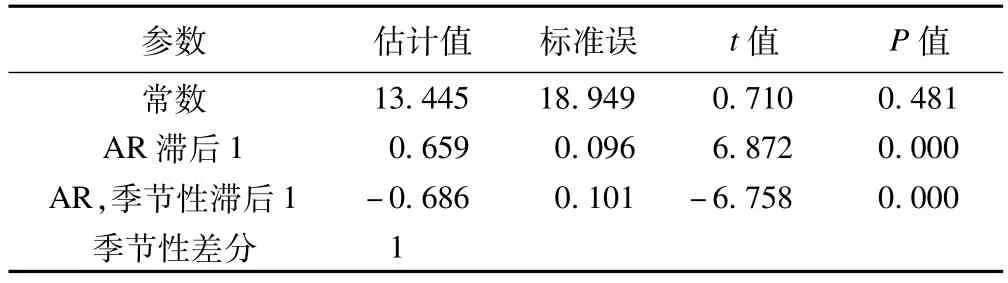
表1 成都市成华区狂犬病暴露监测数的ARIMA模型参数估计
5.预测效果分析
应用模型ARIMA(1,0,0)(1,1,0)12对2009年1月-2015年12月的狂犬病暴露数进行回代预测,结果显示拟合值与实际值基本保持一致的曲线趋势,且实际值均在预测可信区间内,预测均方根误差为28.79,平均绝对误差为82.36,平均绝对误差百分比为9.08%,见图2和表2。同时预测2016年狂犬病暴露数显示,2016年各月狂犬病暴露数的趋势继续跟历年数据趋势一致,暴露高峰将出现在5~8月,见图2和表3。

图2 成都市成华区狂犬病暴露监测数ARIMA(1,0,0)(1,1,0)12预测模型拟合图
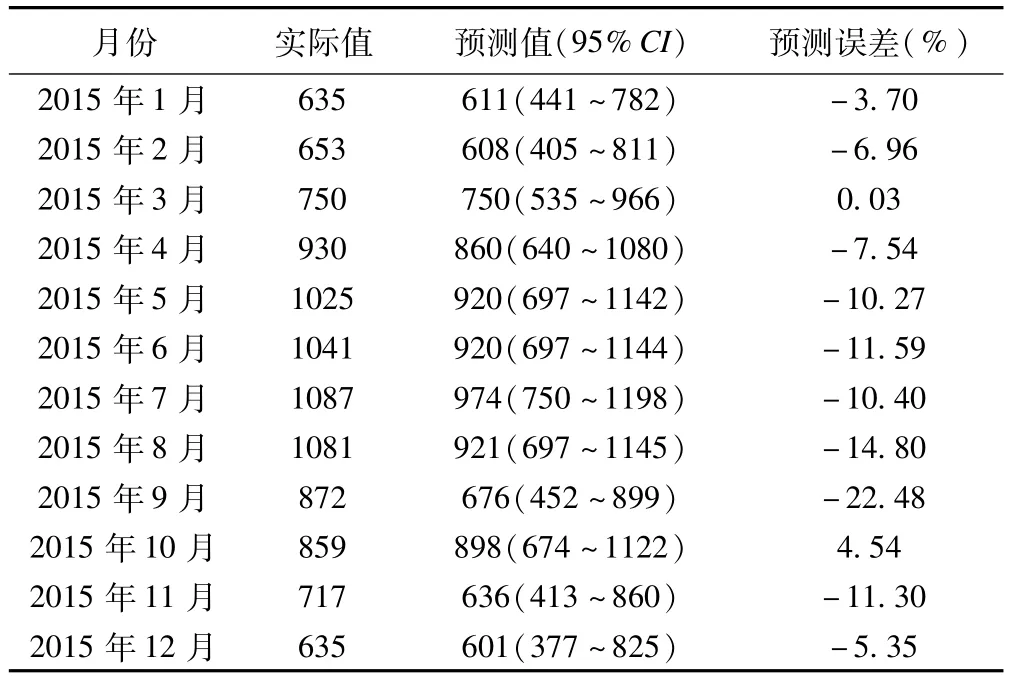
表2 ARIMA(1,0,0)(1,1,0)12模型预测成华区2015年狂犬病暴露数的验证结果
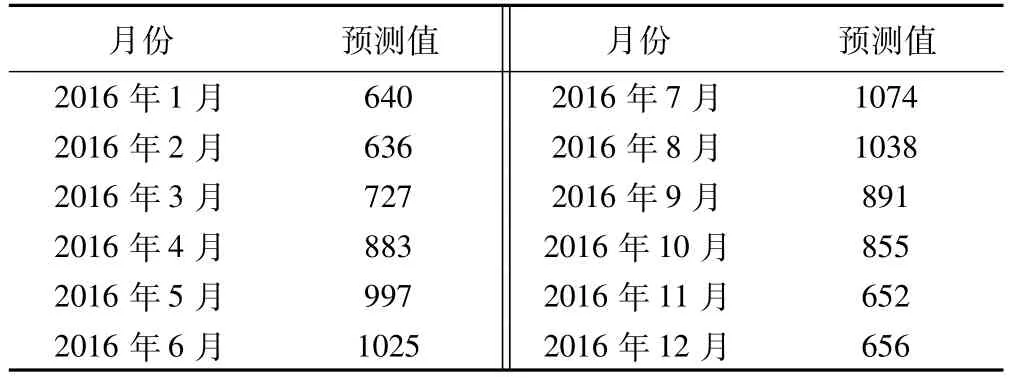
表3 ARIMA(1,0,0)(1,1,0)12模型对成华区2016年狂犬病暴露数的预测结果
讨 论
ARIMA模型是一种精确度较高的短期预测方法,通过季节性差分和非季节性差分削弱序列趋势性及季节周期性的干扰,并结合模型参数对时间序列进行拟合和预测[5]。在利用ARIMA模型对时间序列进行预测时,为保证模型的预测精度至少需要50个以上的历史统计数据[6]。本次研究利用过去6年的狂犬病暴露逐月监测数据,建立ARIMA(1,0,0)(1,1,0)12模型对成都市成华区狂犬病暴露数据进行预测。在实际应用中,需不断用新的数据对已建模型进行修正,提高模型预测的精度[7]。吴家兵[8]等人提出如果网络模型预测对象的惯性趋势发生了较大的变化(如采取了新的防控措施),则需要收集新的数据对模型进行修正或重新拟合。
目前,ARIMA模型已广泛应用于传染病发病的预测[9-12]。在模型的拟合过程中,首先对原始时间序列进行观察,如果未达平稳化要求,则进行差分或(和)季节差分,使其达到平稳化的要求,确定D或(和)d。随后通过对ACF图和PACF图的观察识别,对自回归模型和移动平均模型的p、q进行定阶,产生几个试用模型。依据BIC值诊断模型的拟合优度,并根据简洁、残差不相关的原则筛选出最优模型。本研究最终确定的最优模型为ARIMA(1,0,0)(1,1,0)12。该模型对成都市成华区2009-2015年狂犬病逐月暴露监测数据实际值进行了较好的拟合,回代预测2015年1月-12月狂犬病暴露数预测值与实际值的平均绝对误差百分比为9.08%,显示预测数据与实际数据吻合程度较高,提示利用ARIMA(1,0,0)(1,1,0)12模型能对狂犬病暴露数进行较好的预测。
全国狂犬病年暴露人数逾4000万[13]。狂犬病暴露的监测工作对狂犬病防控效果的评估、防控策略的调整及疫情趋势的预测分析均具有重要意义[14]。本研究结果显示:成都市成华区2009年-2015年的狂犬病暴露数围绕9023例的年平均值上下波动,说明成都市成华区近年积极开展狂犬病暴露监测及暴露后的规范化处置、犬伤处置费用限额报销及健康教育等综合防制措施的成效显著。ARIMA(1,0,0)(1,1,0)12模型的拟合预测曲线显示:每年狂犬病逐月暴露数呈季节性的单峰分布,7、8月份为高峰值月,这与王梅[1]等人研究结果一致;对2016年的预测结果显示:2016年逐月狂犬病暴露数与历年数据趋势一致,暴露高峰将出现在5-8月。
结合本研究的结果,在下一步工作中应继续加强狂犬病暴露数据监测,不断收集和使用新的数据修正预测模型,以提高预测精度,更好地提供参考依据;根据预测值和趋势,科学制定人用狂犬病疫苗的需求计划,做好经费预算,促进犬伤处置费用报销政策的顺利实施;在暴露高峰期加大健康教育工作力度。
[1]王梅,周航,殷文武,等.中国2005-2011年人狂犬病不同地区季节分布特征研究.中华流行病学杂志,2012,33(11):1151-1154.
[2]张文彤,董伟.SPSS统计分析高级教程.第2版.高等教育出版社,2013:395-398.
[3]陈斌,周伴群,焦亮,等.ARIMA模型在狂犬病暴露监测中的应用.中国预防医学杂志,2011,12(5):427-430.
[4]潘浩,郑杨,吴寰宇,等.ARIMA模型预测上海市手足口病发病趋势.预防医学情报杂志,2011,27(6):408-411.
[5]丁磊,丁淑军,张萌,等.应用时间序列分析研究秋冬型恙虫病时间分布特征及趋势.中华流行病学杂志,2012,33(7):698-701.
[6]刘重程,李宏通,唐雅清,等.ARIMA模型在细菌性痢疾预测中的应用.中国预防医学杂志,2011,12(10):842-844.
[7]张越,王胜难,刘媛,等.应用ARIMA模型对呼吸系统疾病月住院量及住院费用的预测.中国卫生统计,2015,32(2):197-200.
[8]吴家兵,叶临湘,尤尔科.ARIMA模型在传染病发病率预测中的应用.数理医药杂志,2007,20(1):90-92.
[9]李骊,钱俊,杨军,等.三种模型对广东省副伤寒逐月发病数预测的比较.中国卫生统计,2014,31(2):197-201.
[10]焦亮,阮峰,黄利群,等.基于ARIMA的流感症状预测模型.实用预防医学,2010,17(8):1482-1486.
[11]吴伟,郭军巧,安淑一,等.应用ARIMA-GRNN模型对肾综合征出血热发病率时间序列数据的预测研究.中国卫生统计,2015,32(2):211-213.
[12]陈伟,陈正利,李少芳,等.ARIMA模型在河南省梅毒月发病率预测中的应用.中国卫生统计,2013,30(4):604-606.
[13]Cui PY,Hang Z,HuiW.Analysis on Factors Related to Rabies Epidemic in China from 2007-2011.Virologica Sinica,2012,27(2):132-143.
[14]周兴余,刘学成,张佳珂.2010年四川省狂犬病监测.预防医学情报杂志,2012,28(1):34-37.
(责任编辑:刘 壮)
ARIMA Model in Prediction of the Rabies Surveillance in Chenghua District of Chengdu City
Yang Jing,Zhang Qiang
(Department of Epidemiology and Health Statistics,School of West China Public Health,Sichuan University(610041),Chengdu)
ObjectiveTo understand the basic characteristics of rabies surveillance data in Chenghua district of Chengdu.To establish ARIMA model based on rabies surveillance data collected from recent years,and to forecast the rabies exposed data from January to December in 2016 in Chenghua district,with the purpose of providing evidence for the standardization construction of dog injury clinic and demand planning of rabies vaccine and rabies immunoglobulin.MethodsSPSS 19.0 was used to establish ARIMA model based on the monthly rabies surveillance data from 2009 to 2014,and case numbers of rabies exposed from January to December in 2015 were used as sample to examine the model accuracy.The optimal ARIMA model was used to predict the monthly rabies exposed numbers in 2016.ResultsThe optimal ARIMA model was ARIMA(1,0,0)(1,1,0)12,which could fit very well with the rabies exposure series in the past period of time.Case numbers of rabies exposed from January to December in 2015 were used as sample to exam ine the model accuracy,the results showed all actual values fell in the 95% confidence intervals of expected values,the mean square error was 28.79,the mean absolute error was 82.36,the mean absolute percentage error was9.08%.ConclusionARIMA(1,0,0)(1,1,0)12could simulate the trend of rabies exposure in the Chenghua district of Chengdu,and can be applied for forecasting the case number of rabies exposed.
Rabies;Surveillance;ARIMA model;Prediction
1.四川大学华西公共卫生学院流行病与卫生统计学系(610041)
2.成都市成华区疾病预防控制中心
△通信作者:张强,E-mail:qiangzhang@scu.edu.cn
