SARIMA模型与SARIMA-GRNN组合模型在预测广东省登革热疫情中的应用*
2017-01-09南方医科大学公共卫生学院生物统计学系510515魏仁惠子沈双全欧春泉
南方医科大学公共卫生学院生物统计学系(510515) 魏仁惠子 沈双全 欧春泉
SARIMA模型与SARIMA-GRNN组合模型在预测广东省登革热疫情中的应用*
南方医科大学公共卫生学院生物统计学系(510515) 魏仁惠子 沈双全 欧春泉△
目的应用季节性差分自回归滑动平均(SARIMA)模型以及与广义回归神经网络的组合模型(SARIMA-GRNN)预测广东省登革热的月发病数,比较其预测效果,为登革热的预测预警和防控提供科学依据。方法该研究使用广东省2004年1月至2012年12月登革热的逐月发病资料,分别构建两种模型,并使用2013年1月至12月的数据对模型进行预测验证。结果登革热疫情呈现明显的周期性和季节性,周期为1年,8~10月份为高发期,在爆发年份发病人数急剧增多。SARIMA(1,1,3)(1,1,0)12模型为SARIMA预测部分的最优模型;神经网络的最优光滑因子为0.04。两种模型对2013年疫情预测的均方根误差(RMSE)为SARIMA(105.76)>SARIMA-GRNN(92.77),平均绝对百分比误差(MAPE)为SARIMA(2.78)>SARIMA-GRNN(2.15),平均绝对误差(MAE)为SARIMA(64.75)>GRNN-ARIMA(58),模型的决定系数(R2)为SARIMA(0.92)<SARIMA-GRNN(0.95)。结论两种方法均有较佳的预测效果。在SARIMA模型的基础上,结合GRNN模型可进一步提高预测精度。
自回归滑动平均模型 广义回归神经网络 登革热 预测
登革热是由登革热病毒引起的一种急性传染病,主要通过伊蚊叮咬传播。其传播迅猛、发病率高。近年,随着旅游业发展迅速、全球气候变暖,登革热疫情日益严重,已成为世界性的严重公共卫生问题。据世界卫生组织估计,全球每年约有5千万至1亿人感染登革热。我国广东地区具有典型的亚热带气候,一直是登革热高发地区。对登革热疫情的有效防控需要及时、准确地了解疫情的动态,对疫情提早进行预测。基于线性假定的自回归滑动平均混合模型(ARIMA)及其衍生模型(如SARIMA)是常见的时间序列预测模型,对于含有许多混杂因素的复杂问题,其预测能力也许欠佳。因而,作为ARIMA模型的补充,广义回归神经网络模型(GRNN)逐渐发展起来。本研究基于广东省近十年的登革热疫情数据,建立SARIMA模型及其与GRNN的组合模型预测登革热的发病情况,并对预测性能进行评估与比较,可为广东地区登革热疫情的预测预警提供科学依据,同时也可为其他地区的同类研究提供方法学上的借鉴。
资料与方法
1.资料来源
数据为广东省2004年1月到2013年12月登革热逐月发病人数,来源于广东省卫生和计划生育委员会网站(http://www.gdwst.gov.cn/)。采用2004年1月到2012年12月数据建立模型,2013年1月到12月数据进行前瞻性考核,验证模型的有效性。
2.方法原理
(1)SARIMA模型[1-2]
Box和Jenkins提出的差分自回归滑动平均模型(autoregressive integrated moving average model,ARIMA)是最基础也是最常用的时间序列预测模型,它由自回归(AR)模型和移动平均(MA)模型组合而成。季节性差分自回归滑动平均模型(seasonal autoregressive integrated moving average model,SARIMA)建立在ARIMA模型的基础上,加强了对季节性和周期性的分析。SARIMA(p,d,q)(P,D,Q)S模型的数学表达式为:

其中t表示时间,zt表示逐月登革热发病人数,μ表示常数项,B表示滞后算子,αt是误差项,函数φ(B)、Φ(BS)、θ(B)、Θ(BS)分别表示如下:
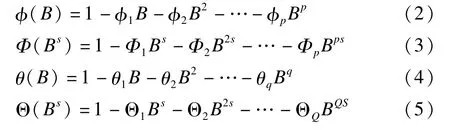
构建SARIMA模型的基本步骤包括:数据预处理、模型识别、参数估计、模型诊断及预测。
(2)SARIMA-GRNN组合模型
广义回归神经网络(general regression neural network,GRNN)是径向基函数的分支,是一种基于非线性核回归的前馈式神经网络,GRNN不需要设定模型的形式,但是其隐回归单元核函数中光滑因子的取值对网络有很大影响[3]。
GRNN训练过程只需改变光滑因子来调节各个单元的传递函数,以获得最佳的回归估计结果。常用的光滑因子确定方法是在学习样本中除去两三个待估点,其余的作为训练样本,让光滑因子在一定范围内按某一增量变化[4],待估点通常随机选取[5-8]。然后对待估点进行测试,将输出的测试值与待估点实际值的误差平方和(sum of square for error,SSE)作为网络性能的评价指标,选取使SSE最小的光滑因子作为最优光滑因子。由于人为控制的参数只有光滑因子,网络的学习全部都依赖于样本,所以使网络最大程度地避免了人为主观因素对网络构建的影响[5-6]。
SARIMA-GRNN组合模型是将SARIMA模型获得的拟合值作为广义回归神经网络的训练输入样本,以月发病数的实际值作为训练的目标输出样本来训练网络。然后使用最优光滑因子构建的网络对后续登革热疫情进行预测。
(3)模型评价指标
采用以下指标评价模型的预测准确性:均方根误差(RMSE),平均绝对误差(MAE),平均绝对百分比误差(即相对误差,MAPE)以及决定系数R2。各指标的计算方法如下:
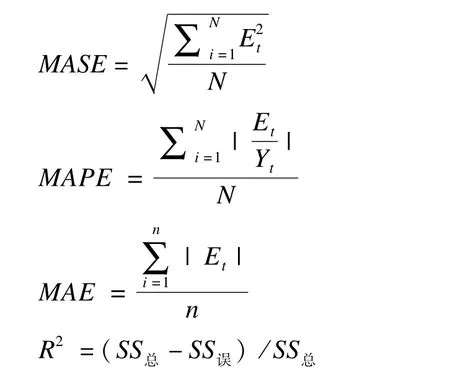
其中,N表示待分析时间序列的长度,即时间点的个数;Et表示预测误差,即实测值与预测值之差;Yt为时间序列的实测值。SS总为实际值的离均差平方和,SS误为误差项的离均差平方和。
3.统计软件
利用SPSS20.0软件构建SARIMA(p,d,q)(P,D,Q)S模型,利用MATLAB 8.1.0的神经网络工具箱编程实现SARIMA-GRNN模型的构建。
结 果
1.登革热疫情的季节性特征
2004年到2012年广东省登革热每月发病数见图1。9年期间共报告登革热病例2173例,死亡0例,年均发病率为2.32×10-6。由图1可以看出,登革热的发病有明显的周期性和季节性特征,周期为1年,8~10月份为发病高峰期,其他月份发病人数则较少。不同年份登革热疫情的流行强度存在明显的差别,2006、2007和2012年夏季均存在暴发流行。
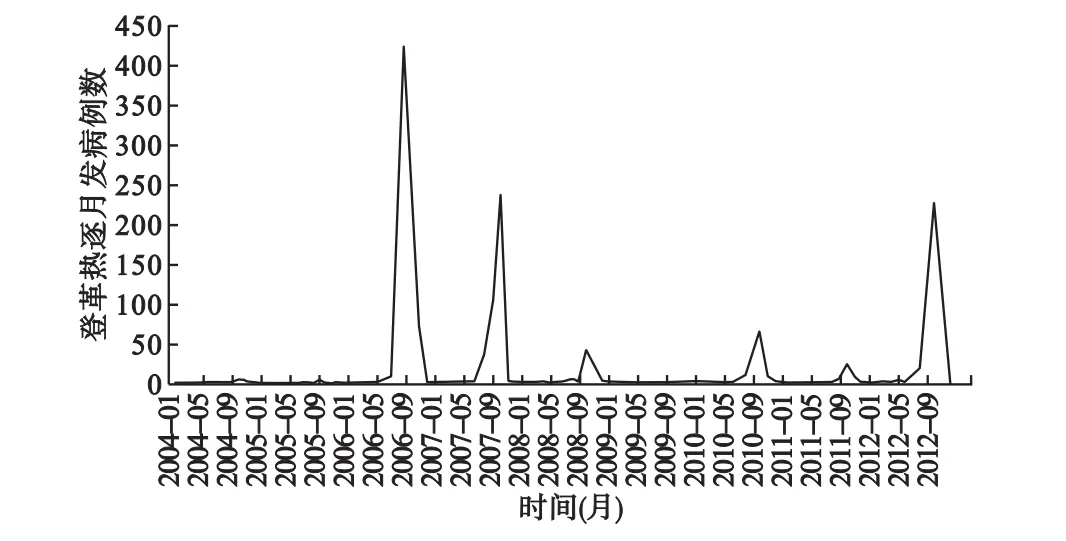
图1 2004-2012年广东省登革热逐月发病人数时序图
2.模型的构建
(1)SARIMA模型
SARIMA模型的建模是以平稳为前提的,为了使序列平稳,先对该数据进行预处理。从图1可以看出数据离散程度较大,故对数据进行对数转换;周期为1年且年份间发病人数差异较大,因此进行季节差分,发现序列仍然非平稳,故进一步对序列进行一阶差分,对差分后的数据做单位根检验,结果显示序列平稳(t=-9.41,P<0.001)。
根据以上的分析,我们尝试建立SARIMA(p,d,q)(P,D,Q)S模型。之前进行了一阶差分和一阶季节差分,因此d=1,D=1。决定采用不同阶数的ARIMA模型建模,根据BIC最小化准则并结合R2值确定模型参数。最终选定最优模型为SARIMA(1,1,3)×(1,1,0)12模型。
用所确定的SARIMA(1,1,3)×(1,1,0)12模型对模型的各参数进行估计,发现各参数均有统计学意义,得到拟合的SARIMA模型为:
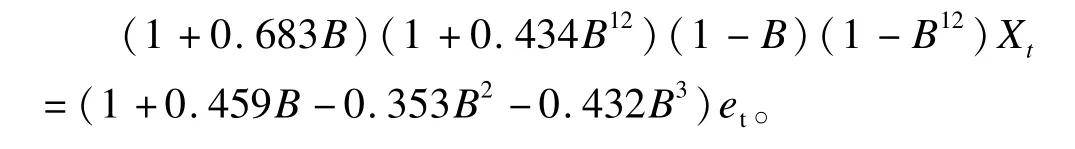
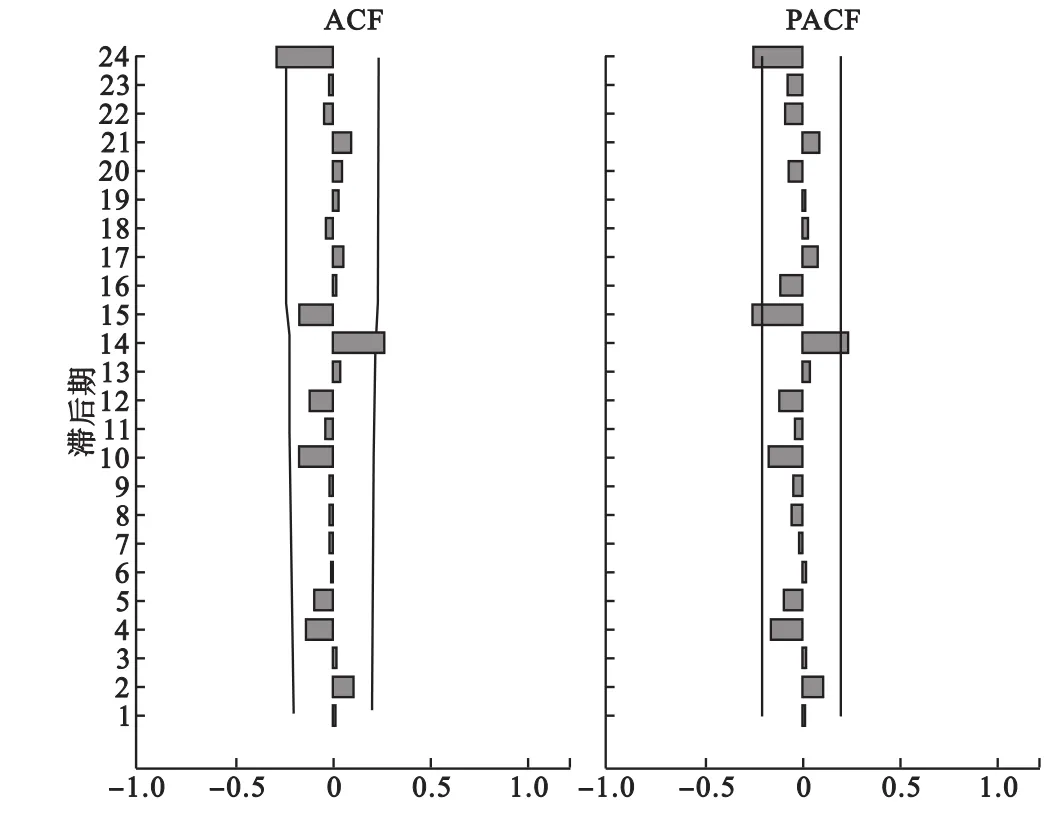
图2 残差序列的ACF及PACF图
由图2可见,残差序列的自相关函数与偏自相关函数基本都在95%可信区间范围内,Box-Ljung检验没有统计显著性(Q=19.953,P=0.096),认为残差序列为白噪声。利用该模型对2013年登革热逐月发病数进行预测,预测值分别为:2,6,22,10,36,22,76,123,550,1386,569,19。
(2)SARIMA-GRNN组合模型
ARIMA模型中进行了差分,导致13个数据丢失[4],随机选取2006年8月和9月的数据作为网络的测试样本(测试样本即代估点),其余的93个数据作为网络的训练样本。为了使网络能够更快地收敛且消除量纲的影响,先对数据进行归一化处理,使用[y,ps]=mapm inmax(x,m invalue,maxvalue)函数,将数据归入0到1之间。光滑因子从0.01到1以0.01的增量递增,每个光滑因子对应不同的SSE值,发现误差平方和在光滑因子处于0.02到0.06之间得到最小值,改变阈值,画出光滑因子对应的SSE值的图形,当光滑因子为0.04时,SSE值最小,约为0.0026547,故确定GRNN模型的spread=0.04。而后将最优spread值代入神经网络,得到2013年的预测值,对该预测值进行反归一化,使用函数y=mapminmax(‘reverse’,x,ps)。得到反归一化后的值分别为:11.7,12.1,14.2,12.6,16.6,14.2,29.5,65.8,477.1,1315.4,598.8,13.8。
3.两个模型预测效果的评估和比较
两个模型对2013年登革热的预测值序列与实际值的吻合程度如下图(图3)。由图看出,两种模型的整体拟合效果都较好,而SARIMA-GRNN组合模型预测出来的趋势与实际发病情况更为吻合,尤其对于峰值的拟合效果要优于单纯的SARIMA模型。
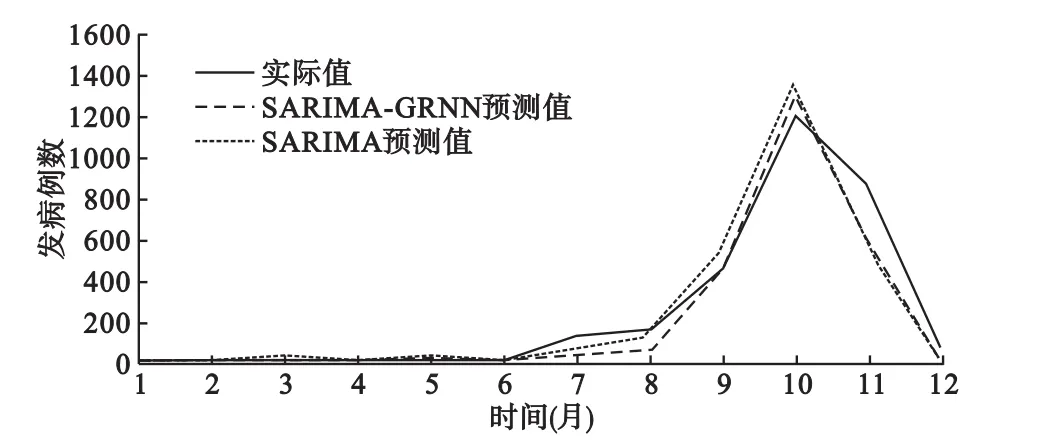
图3 两种模型对2013年登革热发病数的预测值比较
关于预测效果的具体评价指标见表1。相对于单纯的SARIMA模型,SARIMA-GRNN组合模型的均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)更小,决定系数更大,表明组合模型能更准确地对登革热疫情进行预测。
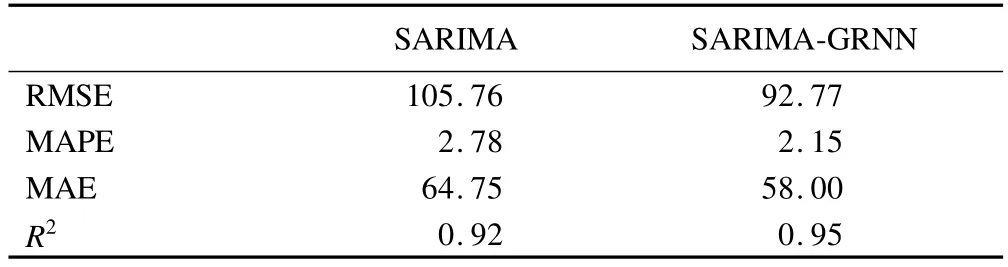
表1 SARIMA与SARIMA-GRNN模型的预测效果比较
讨 论
时间序列的预测模型很多,每种方法都有其自身的优点和不足,SARIMA模型是一种短期预测精度高的模型,基于线性模型估计的特点,使其在面对复杂的含有多重影响因素的问题时,预测精度往往会下降。GRNN神经网络是一种基于非线性理论的更具灵活性的神经网络,学习速度快,对模型的逼近能力强[3-4,6]。能够以任意精度逼近任意非线性连续函数,对非线性的数据映射能力很强,且GRNN的训练过程不需要迭代,其网络训练只需要确定一个参数,训练过程快捷,因而在对疾病的预测中广泛应用[7-8]。
在预测某一事物的发展状态时,单一使用某一种方法或模型可能会有局限性,这时组合模型应运而生。理论和实践的结果均证明了组合模型的预测效能更优于单纯模型,合适的组合模型能够更大程度地挖掘数据间的潜在联系,可以很好地提高预测精度,其模型也更稳定。当然,在构建组合模型时,我们也不只考虑各模型的预测精度,也要基于数据本身的特点选择合适的组合模型。
目前国内对于登革热的研究,大多集中在对登革热的爆发、流行等流行病学方面的分析以及登革热病例的临床分析,而很少有文献涉及登革热的发病预测。本研究将线性SARIMA模型和非线性神经网络相结合,二者取长补短,充分发挥自身模型的优势,使预测效果得到明显提升。登革热疫情的准确预测有助于疾控部门及时采取有效的干预措施,有效地分配健康资源,早期预警也有利于提高人群防患意识,积极加强防控能力。
[1]韩春阳.ARIMA季节乘积模型预测医院门诊量的试验研究.计算机光盘软件与应用,2014,2:72-74.
[2]张蔚,张彦琦,杨旭.时间序列资料ARIMA季节乘积模型及其应用.第三军医大学学报,2002,24(8):955-957.
[3]Zhang G,Huang S,Duan Q,et al.Application of a Hybrid Model for Predicting the Incidence of Tuberculosis in Hubei,China.Plos One,2013,8(11):e80969.
[4]张国良,后永春,舒文,等.三种模型在肺结核发病预测中的应用.中国卫生统计,2013,30(4):480-483.
[5]吴伟,郭军巧,周宝森.GRNN组合预测模型对辽宁省及部分地区肾综合征出血热发病率的预测研究.中国媒介生物学及控制杂志,2008,19(1):44-48.
[6]朱玉,夏结来,王静.单纯ARIMA模型和ARIMA-GRNN组合模型在猩红热发病率中的预测效果比较.中华流行病学杂志,2009,30(9):964-968.
[7]叶晓军,沈毅,任茹香,等.基于GRNN的组合预测模型在传染病发病率预测中的应用.浙江预防医学,2012,24(1):8-13.
[8]严薇荣,徐勇,杨小兵,等.基于ARIMA-GRNN组合模型的传染病发病率预测.中国卫生统计,2008,25(1):82-83.
(责任编辑:郭海强)
Application of SARIMA Model and SARIMA-GRNN Hybrid Model in Predicting Incidence Number of Dengue in Guangdong Province
Wei Renhuizi,Shen Shuangquan,Ou Chunquan
(Department of Biostatistics,School of Public Health and Tropical Medicine,Southern Medical University(510515),Guangdong)
ObjectiveTo apply Seasonal Autoregressive Integrated Moving Average(SARIMA)model and SARIMAGRNN hybrid model to forecast monthly number of Dengue Fever,and compare the prediction performance of these two models.MethodsBased on data of monthly number of Dengue Fever from January 2004 to December2012 in Guangdong Province,we constructed the SARIMA(p,d,q)(P,D,Q)Smodel and SARIMA-GRNN hybrid model,and data from January to December in 2013 were used to assess the predictive validity of models.ResultsThe incidence of Dengue Fever is characterized by an apparent cyclic pattern with a one-year seasonal cycle,with a peak occurring during August to October.The epidem ic strength and peak differed by years.In SARIMA section,SARIMA(1,1,3)(1,1,0)12model is the optimal model.The optimal spread of GRNN model is 0.04.The root mean square error(RMSE)of these two models was SARIMA(105.76)>SARIMA-GRNN(92.77);the mean absolute percent error(MAPE)was SARIMA(2.78)>SARIMA-GRNN(2.15);the mean absolute error(MAE)of the two models was SARIMA(64.75)>SARIMA-GRNN(58);the determination coefficient(R2)was SARIMA(0.92)<SARIMA-GRNN(0.95).ConclusionBoth of the two models had satisfactory prediction capacity.Relatively,the SARIMA-GRNN hybrid model is the optimal model to predict the incidence of Dengue Fever.
SARIMA model;GRNN;Dengue Fever;Forecasting
广东省科技计划项目(2013B021800041);国家自然科学基金项目(81573249);广东省自然科学基金(2016A030313530)
△通信作者:欧春泉,E-mail:ouchunquan@hotmail.com
