二次推断函数与广义估计方程缓控释制剂工艺数据建模比较*
2017-01-09王华芳仇丽霞
王华芳 王 婷 王 祥 魏 珍 范 瑾 武 鹏 张 洁 仇丽霞△
二次推断函数与广义估计方程缓控释制剂工艺数据建模比较*
王华芳1王 婷2王 祥1魏 珍1范 瑾1武 鹏1张 洁1仇丽霞1△
目的比较二次推断函数(QIF)及广义估计方程(GEE)对具有重复测量特征的缓控释制剂制备工艺累积释放度数据的建模效果。方法选取三种作业相关矩阵对缓控释制剂制备工艺正交试验设计数据建立QIF模型并进行拟合优度检验,用评价指标AIC、BIC选择模型及选择合理的作业相关矩阵;基于此合理的作业相关矩阵建立广义估计方程(GEE)模型;用均方误差(MSE)比较QIF模型及GEE模型的建模效果。结果累积释放度数据用QIF方法以可交换相关矩阵建立的模型评价指标AIC、BIC最小(AIC=24.000、BIC=26.367),均方误差MSE=0.0123,而基于可交换相关矩阵建立的GEE模型MSE=32.6535,QIF的建模效果要优于GEE。结论在具有重复测量数据特征的缓控释制剂的建模研究中,二次推断函数建模可以用评价指标AIC、BIC选择模型,并且建模效果优于广义估计方程,具有应用价值。
缓控释制剂 重复测量数据 二次推断函数 广义估计方程
缓控释制剂属于第三代药物制剂,具有定位、定速、定时释放及有效减缓药物“峰谷现象”等特点,克服了普通药物的诸多弊端,具有良好的发展前景。在缓控释制剂处方工艺研究中,需要对具有重复测量特征的工艺评价指标—累积释放度数据建立模型。传统方法建模时要求观测值之间相互独立,不能利用释放度数据相关性的特点,较难得出合理有效的模型。广义估计方程(generalized estimating equations,GEE)可以用于重复测量资料的模型拟合。但是,GEE在模型选择时不能进行拟合优度检验,如果选取作业相关矩阵错误,模型可能会失效[1-2];另外,GEE没有合理有效的指标评价模型效果,只能用均方误差(MSE)估计模型误差大小[3]。二次推断函数(quadratic inference functions,QIF)可以进行拟合优度检验,并且能用AIC、BIC指标评价模型效果,选择出最优模型[4]。本文将对尼美舒利缓释片正交试验设计数据[5]用QIF方法建模及拟合优度检验,然后与GEE的模型比较,为缓释片的处方优化提供更好的建模方法。
资料与方法
1.资料来源
引用文献《尼美舒利缓释片处方优化研究》正交试验设计数据[5]进行分析,影响药物释放的主要因素有3个,即HPMC(x1)、乳糖(x2)、5%PVPK30无水乙醇(x3),每个因素各有3个水平,按L9(34)正交表进行9次试验,评价工艺的指标为2h、6h、12h的累积释放度(Y,%),试验结果见表1。
2.方法
(1)广义估计方程
广义估计方程是1986年Liang和Zeger在拟似然方法(QL)和广义线性模型(GLM)的基础上提出的[6],一种能够分析应变量具有相关性的回归模型。重复测量资料中假设应变量Yij为第i个个体的第j次测量的变量,其中i=1,…,k,j=1,…,t,解释变量为Xij=(Xij1…Xijp),是对应于Yij的p×1维向量。针对模型提出了三个假设:第一,假设Yij的边际期望E(Yij)=μi与解释变量Xij具有线性组合关系,即第二,假设Yij边际方差Var(Yij)与边际期望μi具有函数关系,即Var(Yij)=V(μij)·Ф,其中V(μij)是已知的方差函数,Ф是尺度参数;第三,假设Yij协方差是边际均数μij和参数α的函数,即Cov(Yis,Yit)=c(μis,μit;α)。构造出广义估计方程:

通过解估计方程得到β的一致性估计。其中,Vi=是对角元是Var(Yij)的对角阵,R为工作相关矩阵,包含参数α,如果相关矩阵R被错误估计,回归系数依然具有相合性。

表1 尼美舒利缓释片正交设计方案及结果
(2)二次推断函数
Annie Qu等人在2000年提出了QIF方法,该方法是对广义估计方程的一个推广,是把工作相关矩阵R用一些初等矩阵的线性组合来估计[7],即

其中,I是单位矩阵,M1,M2,…Mm是以0和1为元素的初等矩阵,a0,a1,…am是未知系数,将R-1代入广义估计方程,在广义估计方程的基础上建立一个新目标函数

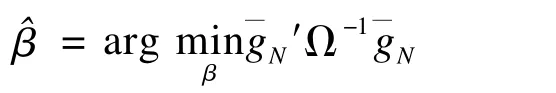
其中Ω=var(gi),假设N个个体是独立的且是恒等分布,应用广义矩估计法的思想,构造β的一个估计,使得中的估计方程gi的线性组合尽可能地趋于0。如果估计方程gi是非线性独立的,那么协方差Ω是可逆的。协方差Ω通常是未知的,它可以通过CN(β)=来估计,且估计结果是一致的。其中要求N≥dim(gi)。通过这种扩展的分向量元素的线性组合,建立一个二次随机函数
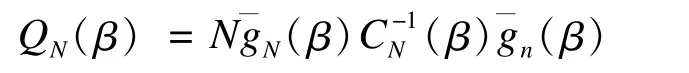
将QN(β)称为二次推断函数,二次函数达到最小的估计值即为参数β的值。
(3)模型拟合及效果评价[8-9]
缓控释制剂研究中需将所有可能的影响因素纳入模型,因此,以累积释放度(Y,%)为反应变量,以x1(HPMC)、x2(乳糖)、x3(无水乙醇)、t(时间)及它们交互作用为自变量,采用可交换相关、一阶自相关、无结构相关三种作业相关矩阵对正交试验设计数据建立QIF全模型,并进行拟合优度检验(统计量为Q),如果检验结果P>0.05,说明模型有意义,指标AIC、BIC值最小者所建的模型较好,模型采用的工作相关矩阵最符合累积释放度数据结构。基于此作业相关矩阵建立GEE模型,并用MSE(MSE=∑SE2)比较两种模型的效果。
3.统计软件
软件SAS 9.1,二次推断函数利用宏语句程序SASMACRO QIF MANUAL:Version 0.2建模,广义估计方程利用程序语句PROC GENMOD建模。
结 果
1.QIF建模及选择合理的工作相关矩阵
采用可交换相关矩阵建立的模型中所有自变量均有统计学意义(P<0.05),而采用其他两种作业相关矩阵建立的模型只有部分自变量有统计学意义。三种模型的拟合优度检验P均大于0.05,说明模型有意义。累积释放度数据以可交换相关矩阵建立的模型AIC、BIC最小(AIC=24.000、BIC=26.367),计算出的均方误差MSE=0.0123。结果见表2及表3。
2.GEE模型拟合
以可交换相关矩阵建立GEE模型,模型系数基本与二次推断函数一致,但是影响因素无水乙醇(x3)与时间(t)的交互作用(x3*t)检验结果没有统计学意义(P>0.05)。计算出评价指标均方误差MSE=32.6535,结果见表4。
3.模型效果比较
基于可交换相关矩阵,用QIF方法建立的模型均方误差MSE=0.0123,用GEE建立的模型均方误差MSE=32.6535,QIF的建模效果要优于GEE。

表2 二次推断函数模型拟合结果

表3 拟合优度检验结果

表4 广义估计方程模型拟合结果
讨 论
缓释片制备工艺试验各时点累积释放度具有相关性,属于重复测量数据,采用传统线性回归等方法是不合理的。二次推断函数是Annie Qu等人在2000年提出的一种对重复测量数据建模的方法[7],能够弥补广义估计方程的不足。二次推断函数不含有讨厌参数,减小了估计的复杂度,提高了估计效率,并且在建立模型之后可以进行和似然比检验类似的拟合优度检验,考察模型是否有统计学意义,可以根据AIC、BIC评价指标选取较好的模型。在一定条件下得到的二次推断函数估计总是相合的、渐近正态的和有效的[1]。广义估计方程没有似然比检验函数,无法进行拟合优度检验,没有合理的评价指标评价模型效果,只能用均方误差MSE估计模型误差大小。
二次推断函数以三种作业相关矩阵建立的模型均有统计学意义,缓释片试验数据适合用二次推断函数的方法建立模型。药物累积释放度数据以可交换相关矩阵用二次推断函数方法建立的模型比广义估计方程模型效果好。因此,尼美舒利缓释片工艺建模可以采用二次推断函数方法以交换相关矩阵建立全模型。以该模型作为尼美舒利缓释片工艺条件优化的目标函数,可以进一步实现优化分析。
本研究只对尼美舒利缓释片工艺建模方法进行了探索性研究,没有进行优化分析,下一步工作可以采用多目标遗传算法进行遗传算法寻优,得到一组可供选择的Pareto最优解集[10],为尼美舒利缓释片的工艺研发提供一个更好的思路。
[1]赵明涛,许晓丽.半参数纵向模型的惩罚二次推断函数估计.统计与信息论坛,2014,29(8):3-8.
[2]杨炜明,廖书,陈相臻.基于改进方差估计的二次推断函数.中国卫生统计,2014,31(1):78-81.
[3]吴秋红,张裕青,李国平,等.不同模型处理纵向缺失数据的模拟研究及应用.中国卫生统计,2013,30(6):855-858.
[4]Serahati S,Biglarian A,Bakhshi E.An assessment of quadratic inference functions method.Turkiye Klinikleri Journal of Biostatistics,2014,6(1):1-7.
[5]梁金英,卢光洲,赵繁荣,等.尼美舒利缓释片处方优化研究.中国药房,2011,22(9):823-825.
[6]Liang K,Zeger SL.Longitudinal data analysis using generalized linear models.Biometrika,1986,73(1):13-22.
[7]Qu A,Lindsay BG,Li B.Improving generalized estimating equations using quadratic inference functions.Biometrika,2000,87(4):823-836(14).
[8]Diggle PJ,Heagerty P,Liang K,et al.Analysis of Longitudinal Data Second edition.Oxford:Oxford University Press,2002.
[9]储岳中.一类基于贝叶斯信息准则的k均值聚类算法.安徽工业大学学报,2010,27(4):410-412.
[10]仇丽霞.基于遗传算法的最优决策值选择及医药学应用研究.太原:山西医科大学,2007.
(责任编辑:郭海强)
Com parison of Generalized Estimation Equation and Quadratic Inference Functions in Modeling Study of the Sustained-release and Controlled-release Formulation
Wang Huafang,Wang Ting,Wang Xiang,et al.
(Shanxi Medical University(030001),Taiyuan)
Ob jectiveTo compare the modeling effects of application of generalized estimation equation(GEE)and quadratic inference functions(QIF)in the modeling of the sustained-release and controlled-release formulation.MethodsEmploys three different work correlation matrixes to establish equation with QIF and according to the test result of goodness of QIF,obtain a suitable work correlation matrix type by AIC and BIC.Based on the suitable work correlation matrix type,GEE and QIF were applied,and results were compared by MSE.ResultsAccording to the test result of goodness QIF,the AIC and BIC are minimal by adopting the exchangeable work correlation matrix type(AIC=24.000、BIC=26.367)and the MSE value is 0.0123.Based on the same work correlation matrix type,GEE were applied in modeling and the MSE value is32.6535,which illustrates the QIF modeling effect is better than that of the GEE.ConclusionIn the modeling of the sustained-release and controlled-release formulation which display repeated and interrelated character,QIF can select the modeling methods by using AIC and BIC criterion,and the QIF modeling effect is better than that of the GEE,so the QIF has value of application.
Sustained-release and controlled-release formulation;Repeated measure data;Generalized estimation equation;Quadratic inference functions
*山西省自然科学基金项目(2013011059)
1.山西医科大学卫生统计教研室(030001)
2.山西省疾病预防控制中心
△通信作者:仇丽霞,E-mail:qlx_1126@163.com
