三塔自锚式悬索桥合理成桥状态研究
2017-01-06丘奕奇赵炜肖汝诚
丘奕奇, 赵炜, 孙 斌, 肖汝诚
(同济大学 土木工程学院,上海200092)
三塔自锚式悬索桥合理成桥状态研究
丘奕奇, 赵炜, 孙 斌, 肖汝诚
(同济大学 土木工程学院,上海200092)
三塔自锚式悬索桥作为一种新兴的自锚式悬索桥体系其在国内的建设方兴未艾。通过对该类桥型合理成桥状态的取得进行了原则和方法上的探讨,给出了一组确定合理成桥状态的具体步骤。同时以某实际工程桥梁为例,验证了该方法可行性,得到了较好结果。
三塔自锚式悬索桥;合理成桥状态;吊索力优化
在我国桥梁工程随着经济发展进入了不断升级创新的阶段,其中自锚式悬索桥作为一种新式桥型受到了桥梁工程师越来越多的青睐。自锚式悬索桥可以省去在软土地基上锚锭的建造费用,还可以为主梁提供“免费”的预应力,在中等跨度的桥梁上取得了一定的经济性优势。同时,自锚式悬索桥还具有较高的美学、社会价值的特点。三塔自锚式悬索桥增加了自锚式悬索桥跨越能力,继承了自锚式悬索桥的优点并满足了较大通航净空的需要,在我国的发展刚刚起步,具有较大发展空间[1-2]。对三塔自锚式悬索桥合理成桥状态的确定有助于提高桥梁建设的合理性和经济性。
1 自锚式悬索桥的受力特点
自锚式悬索桥由主缆、主梁、吊索和主塔组成,其中主缆并非锚固在锚锭上而是锚在主缆的两端。因此,主梁受到了由主缆水平分力产生的轴力影响,在弯曲作用下,将因为轴力的“负刚度”,降低主梁的抗弯刚度,同时,由于主梁竖曲线的影响将产生附加弯矩。此类效应进行叠加,将抵消一大部分主缆受到强大拉力引起的“重力刚度”效应,致使自锚式悬索桥跨径受到限制。这一效应也将地锚式悬索桥与自锚式悬索桥的受力特点显著区分[3-4]。自锚式悬索桥与地锚式悬索桥的主梁受力方程[5]如下所示:
(1)
(2)
其中y为恒载作用下主缆挠度,η为活载作用下主缆附加挠度。可以看出自锚式悬索桥与地锚式悬索桥相比,缺少了地基所提供的主缆轴拉力产生的重力刚度一项,在活载受力方面表现与连续梁更接近,其刚度主要依赖于加劲梁的刚度。
2 三塔自锚悬索桥合理成桥状态的确定方法
2.1合理成桥状态确定原则与方法
合理成桥状态的确定[5-7],是指一座桥在荷载作用确定的情况下,通过调整某些结构参数,使得结构体系在确定的荷载下,某种反映受力性能的目标达到最优。合理成桥状态的设定,一般有刚性支承连续梁法、零位移法等指定受力方式的方法;以及弯矩平方和最小法、弯曲能量最小法、用索(缆)量最小法等制定目标函数的方法。对于斜拉桥而言,可调的参数是斜拉索的索力,对于自锚式悬索桥而言则是吊索索力。
通过调整吊索力达到目标合理成桥状态,需要满足一下几点:在满足力学原理下使目标函数最优;吊索力不发生大的突变;吊索力作用下主梁位移线性平顺不发生突变。
三塔自锚式悬索桥的成桥状态确定时,由于索鞍在施工过程中可以自由滑动,一般假设中跨以及边跨主缆水平分力相等,此时可以通过先中跨再边跨来确定主缆的线型,主塔在该情形下,塔顶水平力相等,塔底弯矩为0或者接近于0,主梁的弯曲应变能占全桥弯曲应变能比重大。对于此种情况,可以采用主梁弯曲能量最小法作为结构优化目标。目标函数为
U=ʃLM2(x)/(2E(x)I(x))dx
(3)
采用有限元软件计算时可以离散为:
(4)
对于自锚式悬索桥主梁,选择吊索对主梁的力为变量,记为fi则主梁弯矩可以写成:
(5)

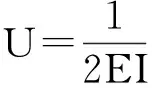
(6)
要使得能量最小,有必要条件
(7)
注意到

(8)
此即为力法方程
(9)
即在水平力给定情况下,弯曲能量最小法等价于刚性支承连续梁法。
2.2三塔自锚式悬索桥的成桥状态确定步骤
三塔自锚式悬索桥的合理成桥状态在主桥参数拟定之后,主缆对主梁的水平力需要进行迭代求出,在初次预估主缆水平力时,可以采用主缆为抛物线形的水平力计算公式H0=ql2/(8f)求得。考虑到自锚式悬索桥单跨跨度不会太大,并且有较大矢跨比,该公式提供了足够的初始精度,且计算相对容易。
三塔自锚式悬索桥的合理成桥状态确定步骤如下:
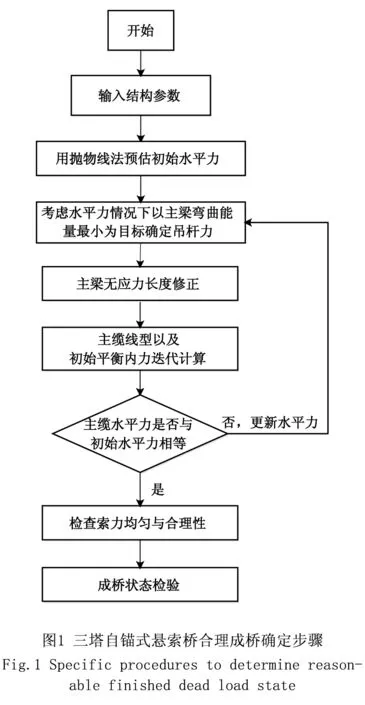
步骤1: 确定桥梁结构总体参数,如跨径、矢跨比、吊索间距等以得到荷载集度;
步骤2:施加主梁荷载集度,估算初始吊索力以及主缆水平力;
步骤3: 将主缆端部水平力施加到主梁上,以吊索力为变量,求得在水平荷载下主梁弯曲能量最小对应的吊索力;
步骤4: 主缆找形以及初始平衡内力计算,用吊索力求得主缆水平力用来来修正原有水平力,检查是否满足收敛条件,若否,则用修正水平力替代原有水平力,重复步骤3。
步骤5:收敛后成桥状态确定。检查索力是否均匀、合理,并对成桥状态进行检验,不满足则重新进行步骤1。
在迭代水平力时,可以使用有限元直接进行主缆迭代得出水平力,也可以采用解析方法求解水平力。该方法对于三塔自锚式悬索桥收敛较快,一般只需几次迭代便可以使计算结果收敛。
2.3 迭代收敛准则
迭代的收敛性有多种选择,常用的指标有水平力误差,最大吊索力误差以及索力差的平方和误差,前两个以及第三个分别对应∞-范数、2-范数。其中前两个较为常用,索力差的平方和可用于多跨悬索桥不对称的情况。对称布置自锚式悬索桥可以使用水平力误差作为收敛准则。
2.4 主梁桥塔无应力修正
自锚式悬索桥加劲梁在受到主缆水平力作用时,主梁将承受压应力,梁的长度将有所缩短。此时主缆在梁端的IP点将移动,主缆的内力也随之变化。为使主缆IP点在求解过程中固定,求解过程中将对主梁施加一温度增量T,使IP点保持不动。如此,在计算中单独对梁施加此温增荷载便可得到主梁的无应力长度值。同理,由于成桥状态下桥塔受到轴压力作用,亦可对其施加一温度增量,保证主缆与塔结合的IP点保持不动。
3 实例分析
3.1 实例介绍
某三塔四跨自锚式悬索桥主桥跨径布置为88m+218m+218m+88m,沿中塔横向对称,全长612m;桥面宽度4.15m,双钢主梁叠合梁断面,主梁高度3.855m,桥梁纵坡为0.5%。设计荷载为公路-I级按八车道计算。主塔高96m,边墩高46.04m,主缆中跨垂度43.6m,矢跨比1/5。实例采用杆系有限元建模,主塔、主梁包括桥面板采用梁单元模拟,主缆以及吊索采用索单元模拟。模型共计节点1 314个,单元1 306个。该模型主塔底部固结,主梁在端部受到扭转的约束(Rx)以及顺桥向(x)以及横桥向(y)的位移约束。主梁与塔弹性连接,限制横向位移约束以及扭转约束。吊索底部与主梁用刚臂进行模拟。
该桥主要截面参数如表1所示:

表1 主要构件截面参数
本文采用ANSYS建立塔梁模型,用于求得弯曲能量最小对应的吊索力,同时使用自行编制的PuCable程序对主缆进行找形,将各主缆初始应变输入ANSYS,将两者模型组装得到合理成桥状态。
3.2 吊索力计算结果
由梁端往跨中,记吊索号为#1、#2…#66,由对称性,取#1至#33结果列出,如图2所示。
由图2所示,吊索力结果总体上呈均匀布置,在主塔附近有较大突变。该突变由主塔附近吊索间距增大、梁截面增加以及设置混凝土双结合段引起。
端吊索力与其相邻吊索变化不大的原因,是主缆与主梁锚固的IP点设置在主梁形心以下,如此在杆系模型中,主梁端部将出现较大负弯矩。但此时可以大量减低端吊索索力,对于结构受力而言,是更加合理的。主缆与主梁锚固IP点的处理方式对比如图3所示。
3.3 主梁弯矩及应力结果
合理成桥状态下弯矩如图4所示,除端部有较大幅度的负弯矩外,主梁各处弯矩成连续锯齿状分布,符合目标要求。



合理成桥状态下,主梁各组成部分应力状态如表2所示。

表2 成桥状态主梁应力绝对值最大值
如表所示,主梁受到强大水平力作用,钢与混凝土在成桥状态下皆呈受压状态。
3.4 主缆吊点坐标及无应力长度
通过解析算法程序PuCable,可以求得成桥状态下主缆各吊点距离中塔正下方桥面板标高的竖向坐标,并求得其相应段无应力长度。该结果分别以图5以及表3、表4所示。


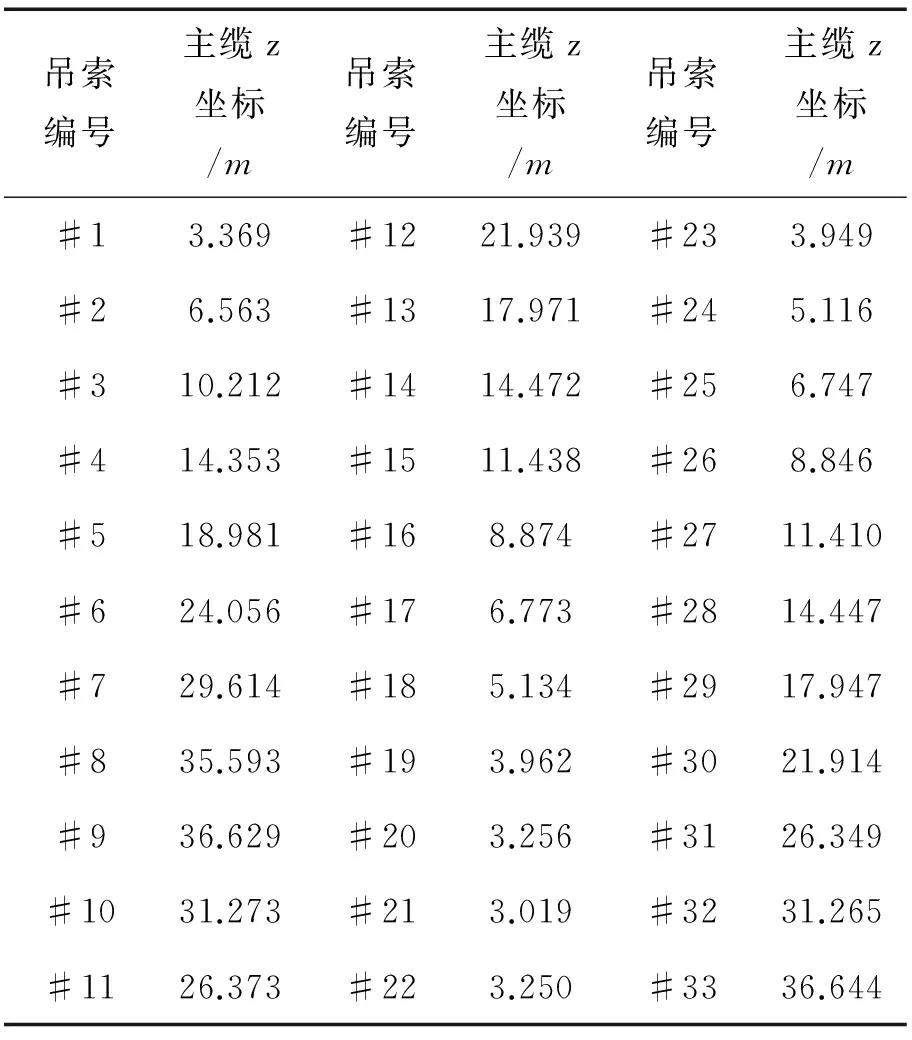
表3主缆吊点竖向坐标(半幅)

表4各吊点间主缆无应力长度(半幅)
表4中各段无应力长度,尚未考虑鞍座对主缆无应力长度影响等因素,为计算理论中的无应力长度。
4 小结
本文讨论了三塔自锚式悬索桥合理成桥状态的取得方法,明确了其主梁最小弯曲能量法的取值以及水平力相等时与刚性支承连续梁法的等价性,给出三塔自锚式悬索桥合理成桥状态的确定方法与步骤。然后,通过某实例三塔自锚式悬索桥,对该成桥状态确定方法进行验证,证明该方法能快速、合理地取得三塔自锚式悬索桥的合理成桥状态。
[1]肖汝诚.桥梁结构体系[M].北京:人民交通出版社,2013.
[2]逯东洋,肖汝诚,孙 斌,等.三塔自锚式悬索桥经济性能研究[J]. 河北工程大学学报:自然科学版,2016,33(2):49-52.
[3]张元凯,肖汝诚,金成棣.自锚式悬索桥的概念设计[J].公路,2002(11):46-49.
[4]GIMSINGNJ,GEORGAKISCT.Cablesupportedbridges:conceptanddesign[M].JohnWiley&Sons, 2011.
[5]石 磊,刘春城,张 哲.自锚式悬索桥挠度理论基础微分方程近似推导[J].哈尔滨工业大学学报, 2004, 36(12): 1733-1735.
[6]谭冬莲.大跨径自锚式悬索桥合理成桥状态的确定方法[J].中国公路学报, 2005(2):51-55.
[7]胡建华.大跨度自锚式悬索桥结构体系及静动力性能研究[D].长沙:湖南大学,2006.
(责任编辑 李军)
Research on determination of reasonable finished dead load state of multi - tower self - anchored suspension bridges
QIUYiqi,ZHAOWei,SUNBin,XIAORucheng
(CollegeofCivilEngineering,TongjiUniversity,Shanghai200092,China)
Self-anchoredsuspensionbridgesareincreasinglywelcomedbyChinesebridgeengineersduetoitsanchor-block-freefee-reduction,adaptationtosoftsoilgroundanduniqueaestheticeffects.Thetriple-towerself-anchoredsuspensionbridge,asabrandnewstructuralform,isjustcontinuingitsmassconstruction.Itsprinciplesandanalysismethodswereexplored.Specificproceduresweregiventodeterminethereasonablefinisheddeadloadstateandapracticalprojectwasusedforverificationofthemethod.
Triple-towerself-anchoredsuspensionbridges;reasonablefinisheddeadloadstate;optimizationoftensionforceofhangers
1673-9469(2016)04-0051-05doi:10.3969/j.issn.1673-9469.2016.04.012
2016-07-25
国家重点基础研究发展计划973项目(2013CB036300);国家自然科学基金资助项目(51378387)
丘奕奇(1990-),男,广东梅州人,硕士,主要从事大跨度桥梁结构方面研究。
TU
A
