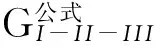I-II-III复合型裂缝应力强度因子与能量释放率的关系
2017-01-06曹晨曦王向东
曹晨曦,王向东,吴 京
( 河海大学 力学与材料学院,江苏 南京210098)
I-II-III复合型裂缝应力强度因子与能量释放率的关系
曹晨曦,王向东,吴 京
( 河海大学 力学与材料学院,江苏 南京210098)
基于断裂力学理论,应用复合型断裂判据中的最大周向应力判据和最大拉应变判据,以单一型裂缝应力强度因子K与能量释放率G的关系为基础,推导出I-II-III复合型裂缝应力强度因子KI、KII、KIII与能量释放率GI-II-III关系公式;并应用有限元软件进行I-II-III复合型裂缝的有限元模拟,模拟值与理论值之间相差为1.14%,拟合良好,分析验证了复合型裂缝应力强度因子KI、KII、KIII与能量释放率GI-II-III关系公式的合理性。
I-II-III复合型裂缝;应力强度因子;能量释放率;有限元模拟
断裂力学是研究带裂纹结构的强度以及裂纹扩展规律的一门学科。很多混凝土结构不可避免的会带缝工作,因此在对带缝混凝土结构的安全分析中,较重要的任务就是研究裂缝的稳定性,而对混凝土结构裂缝安全性分析主要是基于线弹性断裂力学中的K判据与G判据,即分为两种不同的方法:应力强度因子法和能量释放率法。在弹性范围内,应力强度因子K与能量释放率G,是断裂力学中的两个重要断裂参数。因此不仅应该研究它们的计算方法,而且还应该研究二者之间的关系。目前,对单一型裂缝的强度因子K与能量释放率G的关系已有完善的研究和相应的理论公式[1],但在实际工程中,纯单一型裂缝很少,大多数结构所受的荷载都是多向复杂型的,裂缝也是复合型的,因此对于复合型裂缝应力强度因子K与能量释放率G关系的研究是有必要的。本文以带穿透缝的无限大平面板为模型,基于最大应力准则和最大主应变准则,从断裂力学理论入手,并以单一型裂缝以及吴京等[2-6]推导出的 I-II复合型裂缝﹑I-III复合型裂缝和II-III复合型裂缝应力强度因子K与能量释放率G的关系的基础上,推导出I-II-III复合型裂缝应力强度因子KI、KII、KIII与能量释放率GI-II-III的关系公式,并利用有限元软件对其进行分析验证。
1 I-II-III复合型裂缝KI、KII、KIII与GI-II-III的关系
根据线弹性断裂力学理论,I-II-III复合型裂缝可以分解为四种情况:I-II复合型裂缝与III型裂缝叠加;II-III复合型裂缝与I型裂缝叠加;I-III复合型裂缝与II型裂缝叠加;I型裂缝、II型裂缝与III型裂缝叠加。由于I型和II型断裂问题属于平面问题,III型断裂问题属于空间问题,本文采用I-II复合型裂缝与III型裂缝叠加的方法来计算I-II-III复合型裂缝应力强度因子KI-II-III与能量释放率GI-II-III的关系。其应力场以及位移场公式由叠加原理得:
应力场:

(1)
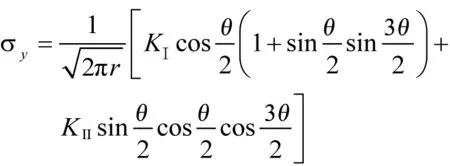
(2)
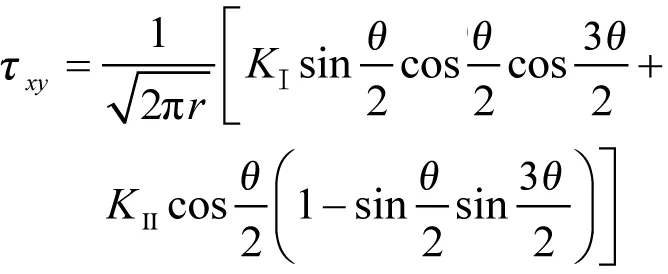
(3)

(4)

(5)
位移场:

(6)
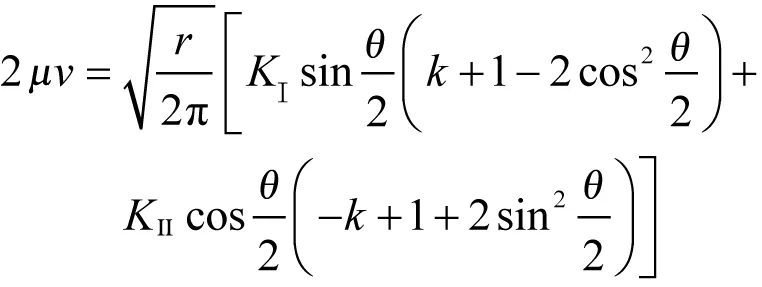
(7)

(8)
由功的叠加原理可得I -II-III复合型裂缝扩展所做的功等于I-II复合型裂缝扩展所做的功、III型裂缝扩展所做的功及I-II复合型裂缝在III型裂缝扩展方向所做的功和III型裂缝在I-II复合型裂缝扩展方向所做的功之和。

如图1所示,I-II复合型裂缝在其扩展方向上扩展的长度为Δm,θ为I-II复合型裂缝的开裂角;纯III型裂缝在其扩展方向上扩展的长度为Δc,其开裂角θ等于0。则裂缝开裂时所需要的能量为:

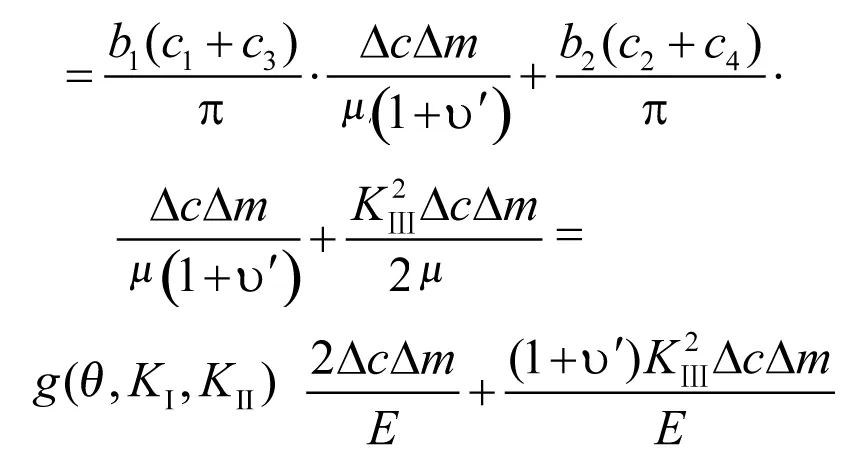
(9)
其中,
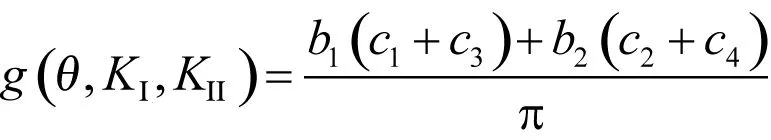
(10)

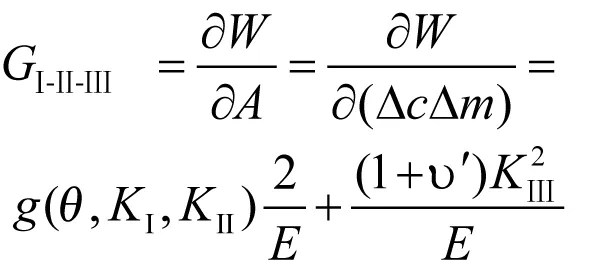
(11)
其中,

(12)
ci为与扩展角θ有关的函数,i=1、2、3、4,具体算式如下:


(13)
其中β=-θ+π。
式(11)即为I-II-III复合型裂缝应力强度因子KI、KII、KIII与能量释放率GI-II-III的关系式。
2 I-II-III复合型裂缝KI、KII、KIII与GI-II-III关系的验证
2.1 公式的退化分析验证
当KII=0,θ=0,KIII=0,且取平面应力状态时,则I-II-III复合型裂缝退化为纯I型裂缝,公式(1-11)可以简化为:

当KI=0,KIII=0,且取平面应力状态时,则I-II-III复合型裂缝退化为纯II型裂缝,公式(11)可以简化为:
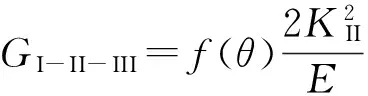
当KI=0,KII=0,且取平面应力状态时,则I-II-III复合型裂缝退化为纯III型裂缝,公式(11)可以简化为:

2.2 有限元分析验证
以带有中心穿透裂缝的结构作为研究对象,应用有限元分析软件ANSYS建立I-II-III复合型裂缝计算模型。有限大板的长度为10 m,宽度为4 m,中心穿透裂缝长为0.5 m,厚度为1 m,面上的拉应力为1 MPa,面内的剪应力以及面外的剪应力都为1 MPa,其荷载和约束情况如图1所示。泊松比为0.167,弹性模量取21 GPa,裂缝尖端设置了24个奇异点,裂缝尖端局部区域网格见图2。
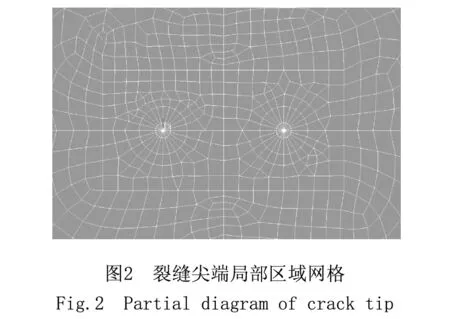
经过有限元软件计算后,得到了I-II-III复合型裂缝的应力图以及应力强度因子K和能量释放率G的数值,图3裂缝尖端区域处应力图。

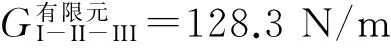
3 工程实例
在某压力容器筒体上有一长为2a=0.2 m的穿透性长裂纹,与筒体周线的倾角为β=45°,筒体壁厚为t=0.1 m,半径为R=5 m,压力p=0.02 MPa。如图4所示,取裂缝周围一有限大板进行受力分析。

根据材料力学的应力状态理论,
可以求得垂直于裂纹线的正应力为
相应的剪应力为
且有
KIII=0
由最大周向应力理论可得,开裂角θ0=-31.37°[8]。
取参数ν=0.25,E=2.1×104MPa,将KI=0.42 MPa·m1/2,KII=0.14 MPa·m1/2,KIII=0 代入式(11)得GI-II-III= 7.6 N/m ,查阅文献[9]得KIc=0.5 MPa·m1/2,KIIc=0.35 MPa·m1/2同上代入式(11)得混凝土的临界能量释放率Gc= 18.2 N/m。显然,GI-II-III [1]王 铎.断裂力学[M].哈尔滨: 哈尔滨工业出版社,1989. [2]吴 京.复合型裂缝应力强度因子和能量释放率的关系[J].济南大学学报:自然科学版,2014,28(6): 425-428. [3]刘梦和.Ⅰ-Ⅱ复合型裂缝应力强度因子和应变能释放率的关系[J].水利水电科技进展,2012, 32(6): 31-33. [4]邵 兵.空间复合型裂缝的性能参数[J]. 水利水电科技进展, 2012, 32(5): 52-55. [5]KAPLANM.F.Crackpropagationandthefractureofconcrete[J].JournaloftheAmericanConcreteInstitute, 1961, 58(5): 591-610. [6]RICEJ.R.Limitationstothesmallscaleyieldingapproximationforcracktipplasticity[J].JournaloftheMechanicsandPhysicsofSolids, 1974, 22(1): 17-26. [7]赵建生.断裂力学及断裂物理[M]. 武汉: 华中科技大学出版社, 2003. [8]洪启超.工程断裂力学基础[M]. 上海: 上海交通大学出版社, 1987. [9]吴智敏.混凝土断裂韧度及临界裂缝尖端张开位移——基于虚拟裂缝模型的分析[J]. 三峡大学学报:自然科学版, 2002,24(1):29-34. (责任编辑 李军) Relationship between stress intensity factor and strain energy releaserate of I-II-III mixed mode cracks CAO Chenxi,WANG Xiangdong,WU Jing ( College of Mechanics and Materials, Hohai University, Jiangsu Nanjing 210098, China) Based on the theory of fracture mechanics,the maximum stress criterion and the maximum principal strain criterion,the relationship between stress intensity factor and strain energy release rate of I - II - III mixed mode cracks was studied. And the I - II - III mixed mode fracture cracks were simulated by using the finite element software. And the relative error between the simulated value and the theoretical value is ,which is within the tolerance range. It is shown that the formula of the relationship between stress intensity factor and strain energy release rate of I - II - III mixed mode cracks is reasonable. I-II-III mixed mode cracks; stress intensity factor; strain energy release rate; finite element simulation 1673-9469(2016)04-0010-04 10.3969/j.issn.1673-9469.2016.04.003 2016-09-12 国家自然科学基金资助项目(50878077) ; “十一五”国家科技支撑计划( 2008BAB29B03) 曹晨曦( 1993-) ,女,江苏泰兴人,硕士,主要研究方向为工程断裂与损伤。 TV313 A4 结论