南水北调南干渠边坡有限元稳定性分析
2017-01-06张坤勇李广山李旺林
张坤勇,李广山,李旺林,杜 伟
(1.河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;2.江苏省岩土工程技术工程研究中心,江苏 南京 210098;3.济南大学 环境与资源学院,山东 济南 250022)
南水北调南干渠边坡有限元稳定性分析
张坤勇1,2,李广山1,2,李旺林3,杜 伟1,2
(1.河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;2.江苏省岩土工程技术工程研究中心,江苏 南京 210098;3.济南大学 环境与资源学院,山东 济南 250022)
采用有限元强度折减法,对南水北调南干渠典型断面进行稳定性分析。计算采用邓肯非线性弹性模型,对渠道边坡的实际开挖施工过程进行模拟。以最大水平位移作为失稳判据,建立最大水平位移和折减系数之间关系曲线,得到不同折减系数下土坡应力变形分布规律和边坡安全系数。计算结果表明,有限元强度折减法,能够较真实地考虑土体应力应变关系和施工过程影响,所得边坡稳定系数略大于毕肖普法计算结果,计算断面稳定安全系数满足规范要求。
有限元;强度折减;边坡稳定; 南水北调;邓肯模型
传统的边坡稳定性分析建立在极限平衡理论基础上,以边坡达到极限状态时土体强度参数的降低程度来评价边坡稳定性[1-2],计算时需要许多假定。大型渠道边坡稳定性计算的目的是为了对渠道稳定性进行合理评估和预测,为设计计算和施工提供参考依据,极限平衡方法只能得到特定条件下单一的边坡安全系数,仅对边坡宏观安全特性进行描述,得不到具体的边坡土体应力及变形分布规律,理论上的安全系数无法结合现场监测结果对边坡稳定进行直观判断和预测。有限元法用于土坡的稳定分析有以下优点[3-6]:可以考虑土体的非线性本构关系,可考虑复杂的荷载及模拟施工过程,从而反映边坡土体真实应力应变关系以及应力历史对土体强度变形特性的影响,使得滑动面上的计算应力比较真实,计算结果更为可靠。本文对南水北调东线工程南干渠的典型开挖渠道断面进行有限元强度折减稳定计算,为渠道边坡的设计、施工和运行管理提供相应安全稳定预测、预警和决策依据。
1 有限元强度折减法
有限元强度折减法通过不断地增加强度折减系数Fs,调整土体的强度指标c、φ,对土坡反复进行有限元分析,以达到临界破坏状态的强度折减系数作为边坡稳定安全系数。随着折减系数Fs不断增加,直至达到临界破坏状态,有限元计算的边坡土体应力和变形也相应变化,从而可以将稳定性和变形量的发展联系起来,建立安全系数和边坡土体变形之间对应关系,如公式(1)、(2)所示:
(1)
(2)
有限元强度折减法的优点是安全系数可以直接得出,并具有明确的物理意义,而该方法的关键问题是临界破坏状态的确定,即如何定义失稳判据。目前主要有三种失稳判据[7]:边坡某个部位的位移或最大位移;土体塑性应变、应力水平等某些内在物理量的变化和分布;迭代求解过程的不收敛。边坡的变形破坏总具有一定的位移特性,因此有限元计算的位移结果是边坡失稳最直观的表达。
以往研究表明[8]:最大竖向位移和水平位移的曲线都适合作为判别是否失稳的标准,但最大的竖向位移往往是边坡后部沉降大的部位,与滑面的位置相差太远,不能代表滑动的特征;而最大水平位移,在各种情况下,和边坡整体的运动具有相似的特征,可以在一定程度上反映边坡的变形过程。所以比较而言,以最大水平位移与折减系数的关系曲线作为失稳判据更合理。本文即以边坡最大水平位移与折减系数关系曲线为失稳判据,并用曲线拐点位置作为极限平衡状态,相应的折减系数即为边坡安全系数。
2 计算程序
本文在河海大学固结有限元计算程序BCF的基础上,应用前述相关失稳判据,编制有限元强度折减边坡稳定计算程序。
2.1本构模型
本文计算中,土体本构模型采用邓肯-张E-ν非线性弹性模型[9-10],切线弹性模量和泊松比分别表示为:
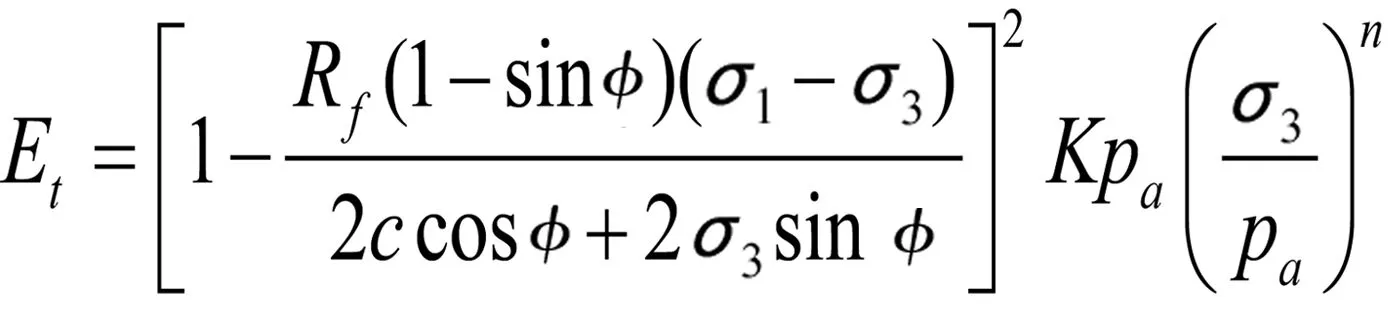
(3)
(4)
其中:
(5)
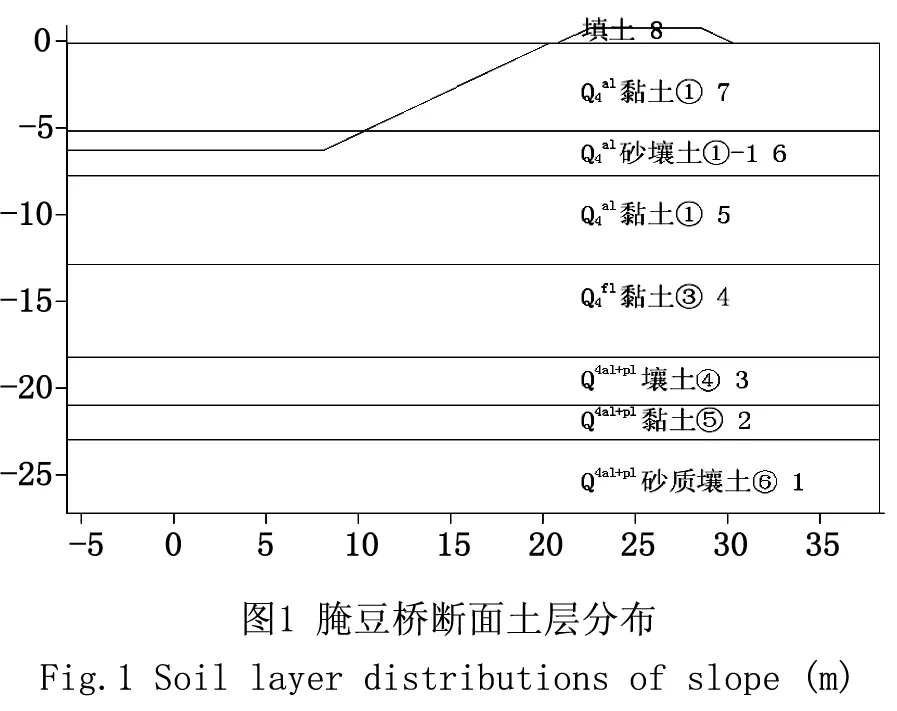
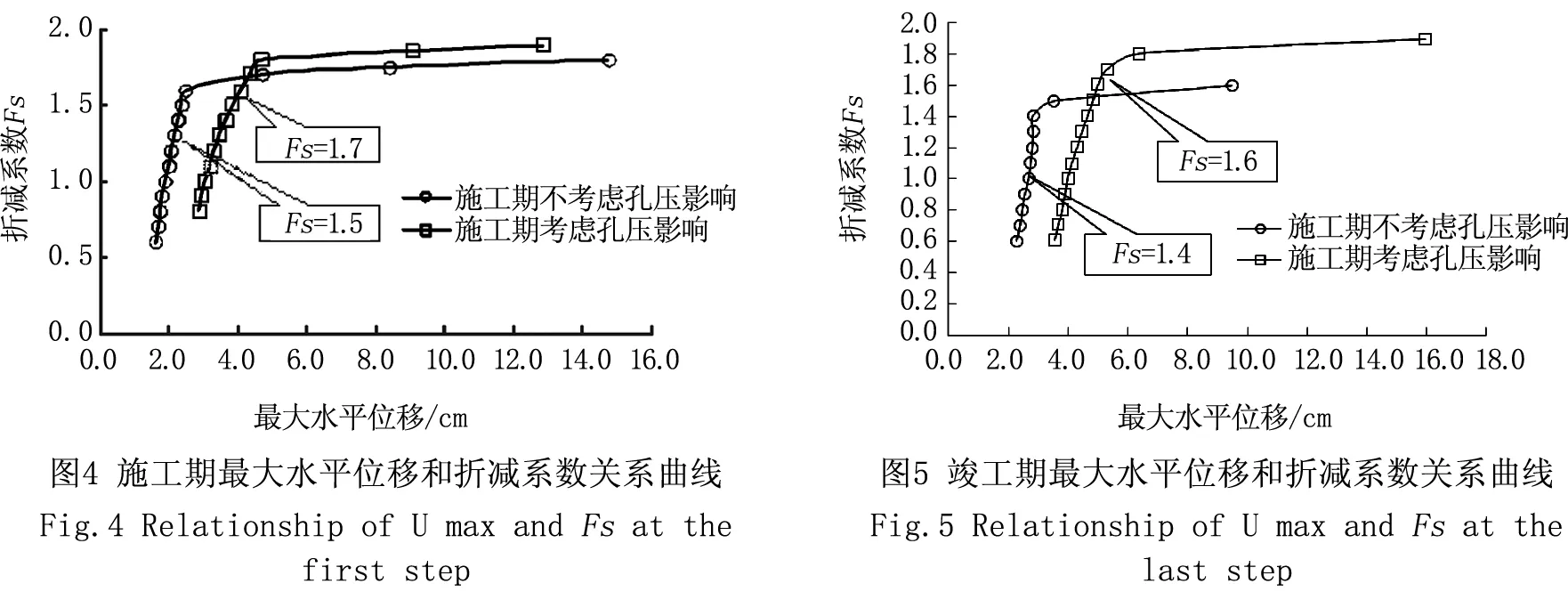
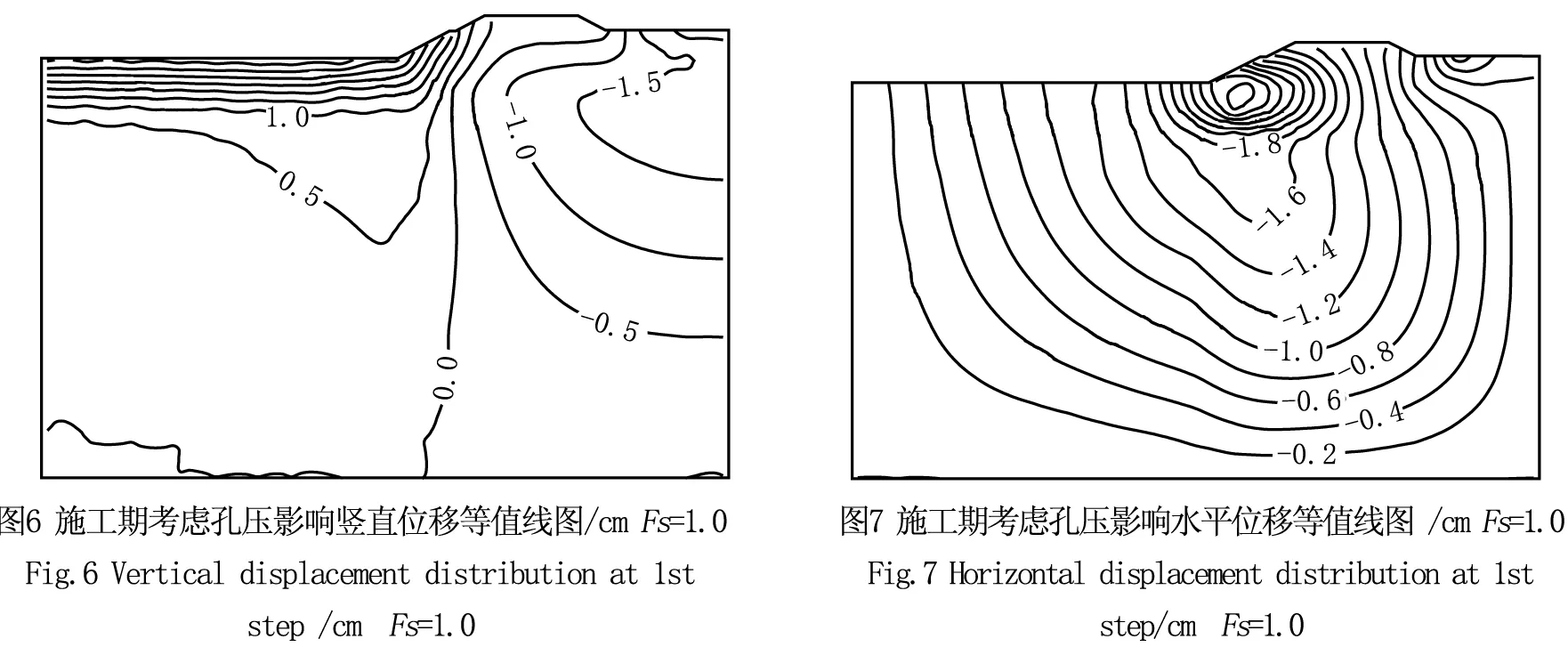
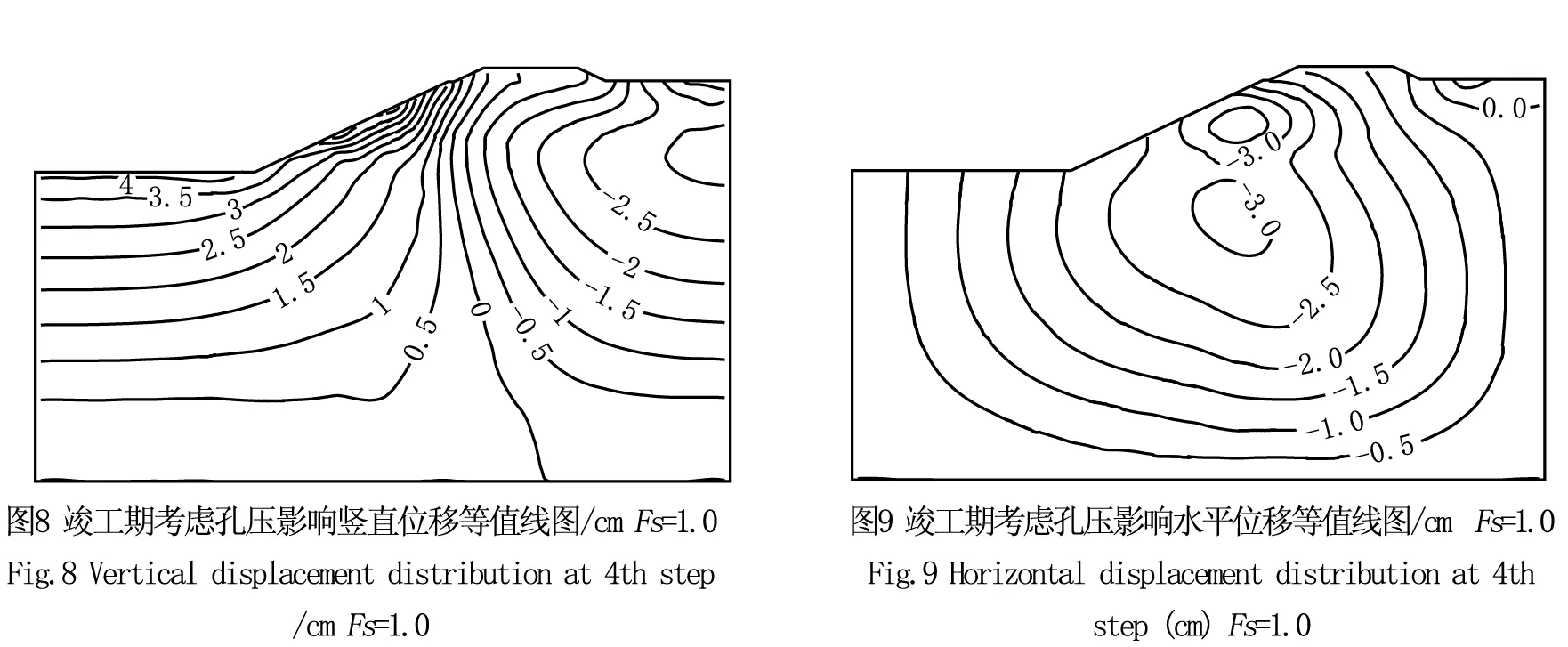
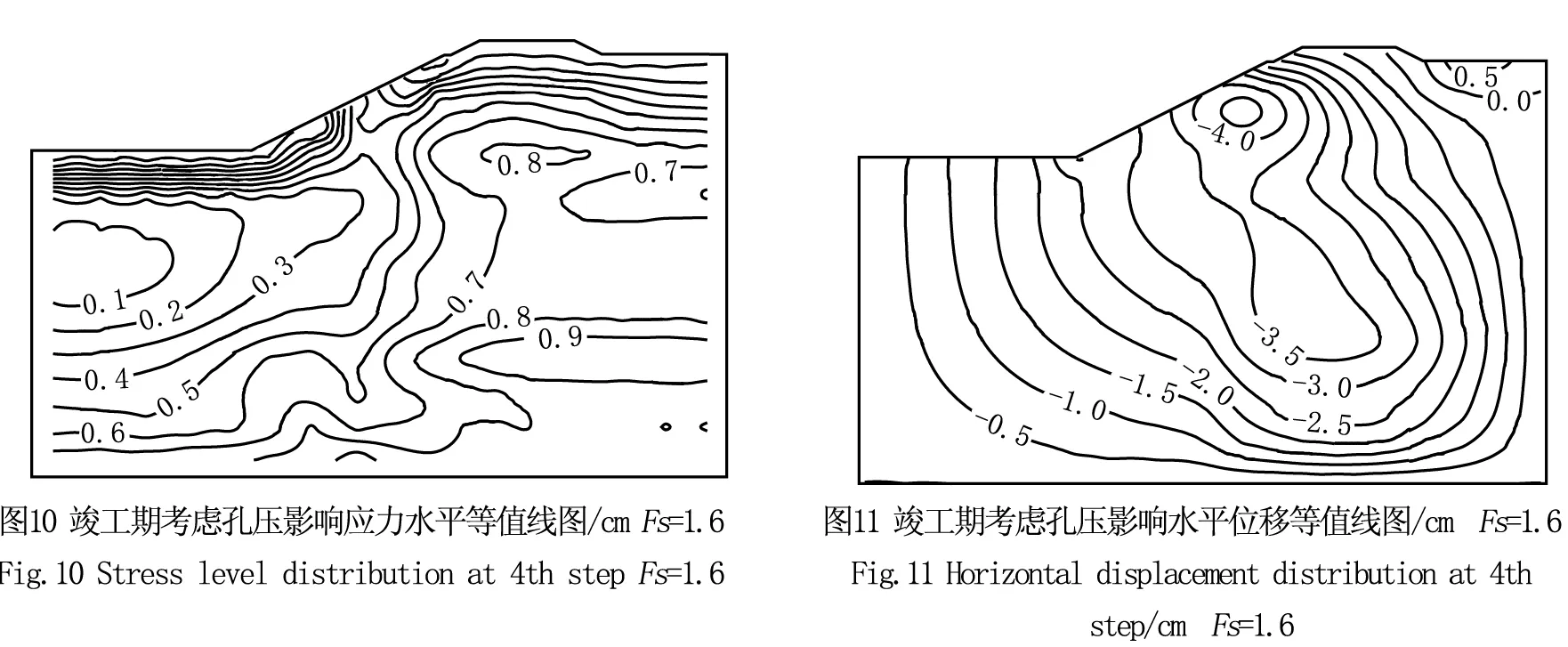
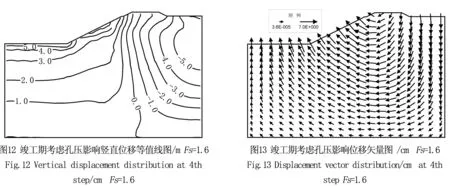
依据邓肯-张模型,对卸荷采用下述方法判别:当σ1-σ3<(σ1-σ3)0,且S 对卸荷情况,弹性模量用下式计算: (6) 式中,c=土体粘聚力; φ=土体内摩擦角;Pa=大气压力;Rf、K、n、G、F、D、Kur为模型参数。 2.2 单元破坏后的应力修正 有限元计算过程中,单元发生破坏后,需对相应单元的应力进行修正,计算才能继续进行。修正的方法是[11]:假定大主应力σ1不变,改变小主应力σ3使其与σ1构成的应力摩尔圆与抗剪强度包络线相切。中主应力σ2则根据修正前后的应力洛德参数不变来确定,即: (7)式中,σ1、σ2、σ3为修正前的三个主应力;σ1′、σ2′、,σ3′是修正后的三个主应力。再根据修正前后的主应力方向不变的原则,求出修正后的6个应力分量。 2.3 开挖卸荷模拟 程序中,对于开挖过程采用如下模拟:第1级荷载计算渠坡开挖前土体的初始自重应力,每级开挖时,将挖去单元的弹性模量取一小值(本程序中取10kPa),在挖去单元节点上加反向等效荷载,以模拟开挖卸荷;如此逐级开挖卸荷,直至开挖至设计标高。绘出相应渠道边坡土体位移和折减系数之间的关系曲线,按照相应安全系数确定方法,进行分析整理,得到不同开挖荷载条件下施工过程阶段以及渠坡竣工完成阶段的安全稳定系数。 南干渠上接穿黄河工程东平湖出湖闸,下连穿黄河工程埋管进口检修闸,是南水北调东线穿黄河工程南岸输水渠段的骨干工程,设计方案为:渠道采用梯形断面,底宽18m,一般挖深6m左右。渠首底高程34.21m,渠末底高程34.13m,纵坡i=1/28 900。 南干渠地处黄泛冲积平原地带,场区地形平坦开阔,土层主要有:裂隙粘土、砂壤土、壤土、粘土、砂质壤土等,可分为七大层:①层裂隙粘土(Q4al),黄褐色,可塑—硬可塑状态,层厚7.10~13.00m,底板高程33.50~27.60m;①-1层砂壤土(Q4al),黄褐色,松散,湿—饱和状态,分布于①层裂隙粘土中部,层厚2.10~3.80m,底板高程34.70~33.00m;②层砂壤土(Q4al),黄褐色,松散,饱和状态,层厚2.30~9.30m,底板高程27.00~23.60m;③层粘土(Q4fl),深灰色,可塑状,粘性很强,层厚0.60~7.00m,底板高程23.00~20.80m;④层壤土 (Q4al+pl):黄褐色夹灰色褐色条纹,可塑状态,底板高程20.50~15.00m;⑤层粘土(Q4al+pl):棕黄色夹蓝灰色条纹,硬可塑状态,粘性很强,层厚2.00~3.00m,底板高程18.50~15.90m;⑥层砂质壤土(Q4al+pl),黄褐色,可塑状态,略有粘性,夹大量细砂粒。土层分布如图1所示: 引水渠设计开挖底高程为34.48m,位于①层裂隙粘土和①-1层砂壤土下部,开挖深度内为①层裂隙粘土和①-1层砂壤土。该两层土均为新近堆积的欠固结土。①-1层砂壤土结构松散,影响边坡稳定,该层具中等透水性,抗渗稳定性和抗冲刷能力差。①层裂隙粘土呈软塑—可塑状,裂隙发育,一般具高压缩性,力学强度不均一,具有失水干裂,遇水软化的典型特征,现多位于地下水位以上,从现有物理力学指标看,物理力学强度并不很差,但工程运用后,受水浸泡饱和后,力学强度会明显降低,工程地质条件变差,影响边坡稳定。 按照《水利水电工程等级划分及洪水标准》(SL252—2000),穿黄河工程为Ⅰ等工程,南干渠等主要建筑物级别为1级。正常运行条件的稳定安全系数允许值为1.30,非正常运行条件的稳定安全系数允许值为1.20。根据《南水北调东线第一期工程穿黄河工程 南干渠工程标 施工图设计说明书》,采用毕肖普法计算腌豆桥断面的安全系数为1.4,以下采用有限元强度折减法对渠道边坡稳定性进行校核。 对南水北调东线工程土质渠道典型断面,腌豆桥断面(设计桩号2+300)边坡,根据提供的边坡土体室内试验资料,考虑渠道边坡挖方实际施工过程,建立符合工程实际的有限元分析物理及几何模型,进行考虑施工过程的有限元强度折减法稳定性分析,并和常规极限平衡方法稳定计算结果进行比较。 4.1 计算模型及参数 计算中,考虑渠道边坡开挖施工过程,一共四级,如图2所示。相应有限元网格如图3所示,计算中采用一次形成网格,通过调整开挖单元的物理力学指标施加开挖荷载以模拟施工过程。为考察开挖中固结过程的影响,分别进行了考虑固结过程和不考虑固结过程的计算,以比较孔压对结果的影响。 计算坐标系在竖直方向(Y方向)以向上为正,水平方向(X方向)以向右为正。计算的变形分布等值线中,由于均为开挖卸荷,竖直方向的位移呈向上回弹,一般为正;水平方向位移为从渠道边坡向渠道内,一般为负。计算断面各土层邓肯模型计算参数见表1。 4.2 渠道稳定安全分析 根据有限元计算结果,分别做出施工开始期(第一级开挖完成后,以下简称施工期)和竣工期(第四级开挖至设计标高)的最大水平位移与折减系数的关系曲线。如图4和图5所示。 表1 腌豆桥断面土层计算参数 图4、图5中,最大水平位移系指由于开挖引起渠道边坡卸荷,导致边坡土体向渠道方向的变形。从图中可见,位移和折减系数曲线呈明显的双曲线形态且拐点位置明显,因此可以用曲线拐点处所对应的折减系数作为渠道边坡稳定安全系数。从上述曲线中,可以明确确定拐点位置对应的位移及折减系数。考虑孔压影响竣工期对应的最大水平位移为4.98cm,计算安全系数为1.6;不考虑孔压影响竣工期最大水平位移为2.89cm,对应的安全系数为1.4。 随着开挖的进行,相应的安全系数会逐渐降低,考虑孔压影响的第一级开挖渠道边坡安全系数为1.5,不考虑孔压影响为1.7;第四级开挖完成后,渠道开挖至设计标高,竣工期不考虑孔压影响的渠坡安全系数为1.4,考虑孔压影响的安全系数为1.6,均大于规范要求的1.3,说明渠道边坡在开挖过程和竣工期均是稳定的。不考虑孔压影响的有限元强度折减法的安全系数计算结果和采用毕肖普方法计算结果基本一致,均为1.4。 4.3 不同开挖阶段渠道边坡位移 图6、图7分别给出了渠道施工期(第一级开挖完成),考虑孔压影响条件下,折减系数等于1.0所对应的渠道边坡土体竖直位移,水平位移。图8、图9分别给出竣工期(第四级开挖完成),考虑孔压影响条件下,折减系数等于1.0所对应的渠道边坡土体竖直位移,水平位移等值线图。从图中可见:由于开挖卸荷,开挖面附近的水平位移和竖向回弹变形均较施工期明显增大,最大水平位移4.01cm和最大竖直位移5.32cm集中在潜在滑弧附近,整个边坡土体变形矢量呈向开挖面发展趋势。 从上述图示可知,随着开挖过程的开展,渠道开挖面上应力水平逐渐增大,水平位移和竖向位移也有所增加,反映在渠道稳定安全系数上,从1.7降低到1.6。从分析可知,对竣工期考虑孔压影响计算方案,Fs=1.6的时候,渠道边坡土体进入临界状态,图10—图13分别给出了在此临界状态下所对应的渠道边坡土体应力水平,水平位移,沉降的等值线图,以及变形矢量图。 根据前面分析,Fs=1.6意味着渠道边坡处于临界滑动状态,和前述Fs=1.0计算结果相比,由于强度折减,大主应力变化不大,但小主应力降低,导致应力水平,尤其是开挖面附近应力水平有所增大;并且在渠道局部转角位置出现连续的应力水平大于1.0区域,说明土体局部发生了破坏;同时,水平位移和竖向回弹变形均明显增大,变形矢量呈明显呈向开挖面发展趋势;最大水平位移的位置由于应力重新分布,也从渠道坡面位置下移,最大水平位移为4.98cm;断面整体位移增加,从位移矢量图可见,开挖面以竖向回弹位移为主,最大竖向回弹变形为6.36cm;从位移矢量图可知,坡顶位移矢量呈圆弧滑动趋势,坡后土体下沉,整个渠道边坡呈临界滑动状态。 南水北调东线工程南干渠典型断面的有限元折减稳定计算结果表明,考虑孔压影响竣工期对应的最大水平位移为4.98cm,计算安全系数为1.6;不考虑孔压影响竣工期最大水平位移为2.89cm,对应的安全系数为1.4,均大于规范规定的要求的1.3。且均较施工期的土坡安全系数有所降低,说明随着开挖过程,渠道安全系数逐渐降低。但南干渠渠道边坡仍然在稳定安全范围内。此外,由于开挖卸荷影响,渠道土体内实际为负孔压,有效应力较不考虑孔压影响的结果大,所以考虑孔压影响的相应安全系数亦较高。 以边坡最大水平位移作为失稳判据具有明确的物理意义,可以作为边坡临界状态的判断标准。根据最大水平位移和强度折减系数关系曲线的曲线特征,不仅可以对既有边坡进行安全性评估,而且也方便对渠道边坡在施工及运行过程中的安全稳定性进行实时监测及预警。 [1]BISHOPW.TheuseoftheslipcircleinthestabilityanalysisofSlopes[J].Geotechnique,1955,5(1): 7-17. [2]MORGENSTERNR,PriceV.Theanalysisofthestabilityofgeneralslipsurfaces[J].Geotechnique,1965,15(1):79-93. [3]DUNCANJM.Stateoftheart:Limitequilibriumandfiniteelementanalysisofslopes[J].JournalofGeotechnicalEngineering,ASCE,1996,122(7):477-596. [4]GRIFFITHSDV,LANEPA.SlopeStabilityAnalysisbyFiniteElements[J].Geotechnique,1999,49(3):387-403. [5]DAWSONEM,ROTHWH,DRESCHERA.SlopeStabilityAnalysisbyStrengthReduction[J].Geotechnique,1999,49(6):835-840. [6]SALGADOJK,YUHS.LimitAnalysisofSoilSlopesSubjectedtoPore-WaterPressures[J].JournalofGeotechnical&GeoenvironmentalEngineering,1999,125(1):49-58. [7]ZHANGYS,WANGHC.NumericalSimulationoftheStabilityofHighSandLoessSlopes[J].JournalofGeomechanics,2004,10(4):357-364. [8]吕擎峰.土坡稳定分析方法研究[D].南京:河海大学,2005. [9]DUNCANJM,CHANGCY.Nonlinearanalysisofstressandstraininsoils[J].JournalofSoilMechanicsandFoundationDivision,ASCE,1970,96(5):1629-1653. [10]KULHAWYFH,DUNCANJM.StressesandMovementsinOrovilleDam[J].JournalofSoilMechanicsandFoundationDivision,ASCE,1972,98(7):653-665. [11]钱家欢,殷宗泽.土工原理与计算[M].北京:水利电力出版社,1996. (责任编辑 王利君) Finite element stability analysis on slope of South Main Canal of South to North Water Diversion Project ZHANGKunyong1, 2,LIGuangshan1, 2,LIWanglin3,DUWei1, 2 ( 1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering,Hohai University, Jiangsu Nanjing 210098,China; 2. Jiangsu Research Center for Geotechnical Engineering Technology,Hohai University, Jiangsu Nanjing 210098,China; 3. School of Resources and Environment,University of Jinan,Shandong Jinan 250022,China) The strength reduction finite element method was used to analyze the stability of the typical section of the South Main Canal of South to North Water Diversion Project. The Duncan - Chang nonlinear constitutive model was employed to describe the stress and strain relationship of the soils. The displacement mutation of the maximal horizontal displacement of the slope was used as a criterion for evaluating the instability. The research results based on the FEM reduction stability analysis was verified by traditional simplified Bishop Method. There is good accordance between both methods,which proved that the analysis is reasonable. And both results fulfil the designation requirement. FEM;Strengthreduction;Slopestability;South-to-NorthWaterDiversion;Duncanmodel 1673-9469(2016)04-0027-06doi:10.3969/j.issn.1673-9469.2016.04.007 2016-06-16 国家自然科学基金资助项目(51578214);中央高校基本科研业务费专项资金资助项目(2015B17714);中国交通建设股份有限公司科技研发项目(2012-ZJKJ-11) 张坤勇(1975-),男,安徽濉溪人,博士,副教授,研究方向为土的基本特性、边坡稳定性分析、岩土工程数值分析等。 TU A3 南干渠工程概况
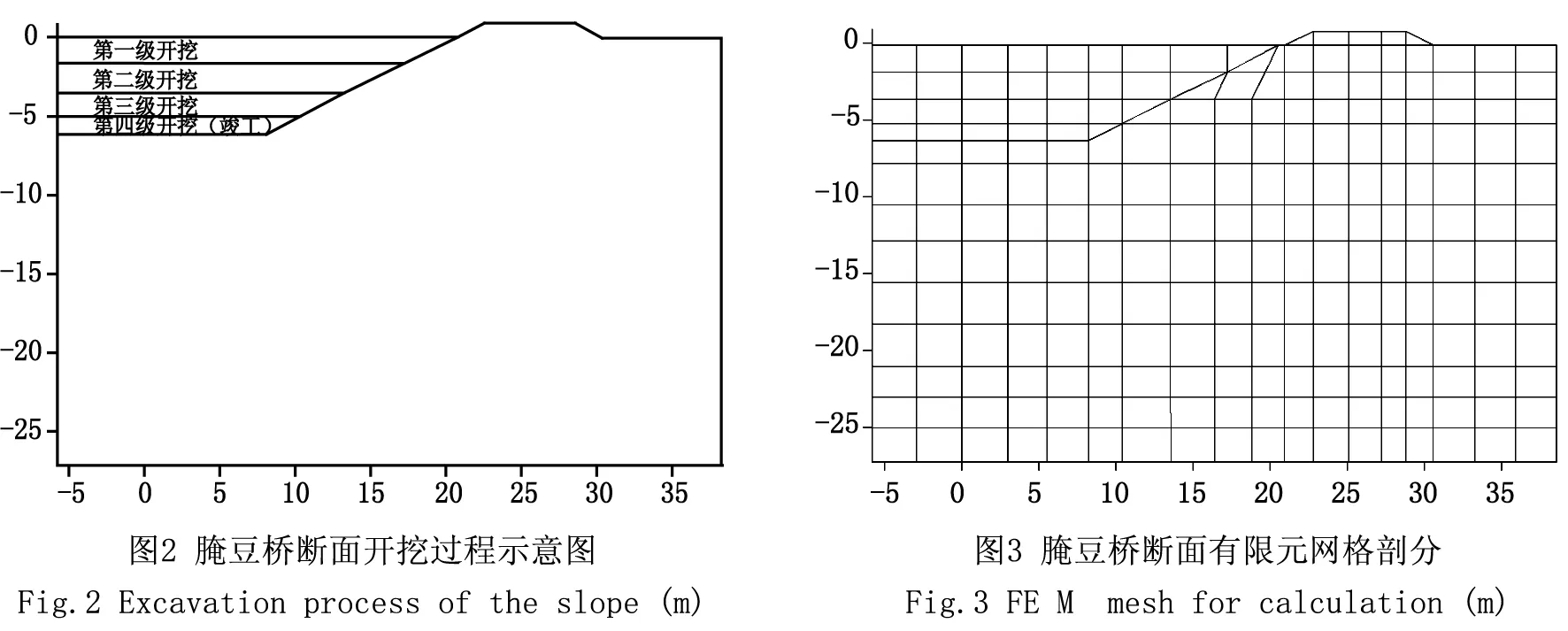
4 南干渠典型断面稳定性分析
5 结论
