加拿大小学数学课程标准中的数感与运算能力评析——以安大略省为例

张文宇，宋 军



加拿大小学数学课程标准中的数感与运算能力评析——以安大略省为例

张文宇1，宋 军2

（1．渤海大学教育与体育学院，辽宁锦州 121013；2．盘锦市鹤乡小学，辽宁盘锦 124000）

加拿大安大略省于2005年颁布了《安大略数学课程（修订）》．数感与运算能力作为小学1~6年级数学课程内容的一个分支，被看作是其它分支的基础．在介绍数感与运算能力核心思想的基础上，分析了各核心思想具有的特征；提出了对中国小学数学课程与教学研究的借鉴与启示．

数感与运算能力；数量关系；计数；运算意识；比例关系

在近年来的PISA测试中，加拿大学生的数学成绩始终位居前列[1~2]．作为教育分权制的国家，加拿大各省可以自行制定、实施课程标准．安大略省（以下简称安省）一流的基础教育水平和成熟、完善的课程框架已经成为加拿大其余各省课程改革的典范．研究者以安省为例，分析加拿大小学数学课程标准中的数感与运算能力，希望对中国的小学数学课程教学研究提供借鉴和参考．

1 数感与运算能力的课程期望

安省小学阶段目前使用的数学课程标准是2005年颁布的《安大略数学课程（修订）》（以下简称《课程标准》），该文件是小学数学教材编写、教学、考试评价的依据[3]．《课程标准》规定小学数学内容主要包含5个分支：数感和运算能力、测量、几何和空间观念、模式和代数、数据管理和概率．其中数感和运算能力这一分支是小学数学的基础．因为数感与运算能力遍及其它数学分支，可以和其它分支的数学教学、数学活动相联系．

《课程标准》将数感和运算能力界定为：对数字和运算的总体理解，以灵活的方式应用这种理解，做出数学判断，为了解决问题发展有价值的策略．在这个分支中，学生通过学习不同的表征数字的方式及数字之间的关系，发展对数字的理解；他们学习以不同的方式计数，发展对“大数”的认识，发展对四则运算的深刻理解，学习使用各种工具和策略流利地计算．发展良好的数字理解包含掌握“多与少的关系”，“部分与整体的关系”，特殊数字（例如5和10）所发挥的作用，数字和现实的量、环境中的测量之间的关系等[4]．根据儿童数学思维发展的特征、规律以及数学课程内容的编排，整个小学阶段的数感与运算能力包含的核心思想也是发展变化的．1~3年级的核心思想包含：数量关系、计数、运算意识；从四年级开始，在此基础上添加了比例关系；六年级不再包含计数．

《课程标准》对小学各个年级的课程期望做了详尽的阐述，为教材的编写、教师的教学提供了具体的、有针对性的指导．课程期望分为总体期望和具体期望，总体期望以一般性、概括性的术语描述了期望学生在各学年结束时所具备的数感与运算能力方面的知识与技能；具体期望则对各年级的核心思想进行具体的阐述，更详细地描述了预期的知识和技能．由于篇幅所限，表1仅列举出各年级的总体期望，各年级的课程期望（包含总体期望与具体期望）见附录．

2 对数感与运算能力课程期望的评析

2.1 数量关系

关注儿童对数字的表征、比较和排序．

数量是对现实生活中事物量的抽象，数量的本质是多与少[5]．理解数字所表征的数量是学生具有数感的重要表现．儿童在入学前就已经了解现实生活中的量，他们知道量之间的大小关系、多少关系．理解数量是理解十进位值制、运算的意义和分数的重要前提条件，是发展学生数感的基础．数量关系课程期望所体现出的最显著特征是关注儿童对数字的表征、比较和排序，促进儿童对数量关系的理解．

第一，关注儿童对数字的表征．在支持学生理解数学概念和数学关系方面，表征是基本的元素．在小学低年级阶段，《课程标准》要求学生表征1 000以内的整数，使用四则运算的符号，分数符号也被引入．到了四年级以后，知识扩展到了1 000 000以内的大数，以及新的符号（小数点、百分号、比）．同时要求使用各种工具（操作硬币、数轴、互相连接的正方体等）表征整数，使用具体的材料（分数条、分数圆和10×10方格纸）、文字和标准的数学符号表征分数和小数、百分数．

第二，关注儿童对数字的比较和排序．在小学低年级尤其在一年级，学生对数量关系理解的证据是能根据大小及多少，对数量比较和排序，认识到数字如何与其它数字相联系．《课程标准》在一年级提出将数字5、10作为“锚”，将0~9的数字与5和10建立联系．这是理解整十数、整百数的重要基础；也能够帮助学生更好地理解数字的组合与分解．当儿童能够分解和组合数字进行运算，他们能够看到数字间的联系，儿童认识和使用数字模式的技能得到提高[6]．而对数字模式的意识是儿童早期数感发展的关键因素[7]．具备数字模式直观把握的学生很容易从已知的组合中得出未知数字的答案，这种能力反过来帮助学生掌握数字的组合与分解．对四~六年级的学生而言，将数字与基准数字相联系是对数字比较和排序有价值的策略．《课程标准》四年级要求将0、、1作为基准数字，比较分数的大小．六年级要求将10%，25%，50%，75%，100%作为基准数字，估计数量．

表1 数感与运算能力的总体期望

2.2 计 数

重视培养儿童灵活的计数策略．

计数是发展低年级学生数感的重要途径和策略．学生在小学低年级阶段学习的数学概念与计数有密切联系．通过真实的计数经验，学生发展基本的概念和策略，帮助他们理解和描述数字，发现数字之间的关系和模式（例如数字0~9之间的关系，10~19之间的关系）．计数技能是学习十进制概念的基础．当儿童开始计数比9大的数字时，他们的十进位值制的概念得到发展．当低年级儿童确定运算问题的答案时，计数是他们最先采用的策略．儿童计数策略的多样性和精确性是衡量低年级阶段儿童数感发展水平的重要指标[8]．低年级学生在计数上存在的缺陷与他们的数学学习困难密切相关，也是影响后续数学学习成就的重要因素[9]．

《课程标准》强调培养学生灵活的计数策略：一一对应是低年级儿童计数的一个重要原则[10]．《课程标准》在一年级要求学生使用具体材料说明数字和计数对象之间的一一对应关系；将向前数和向后数相结合，渗透加法和减法的意识；同时扩展学生的计数模式：除了从1开始，一个一个地计数外，要求学生借助各种工具和策略逐渐掌握每2个、5个、10个一组，以任一数字作为起点进行计数．随着儿童逐渐获得更加复杂的计数技能，计数的对象也从整数扩展到了小数、分数和百分数．《课程标准》要求一~三年级涉及到整数的计数；四、五年级涉及到分数、小数的计数；六年级对计数不做要求．

2.3 运算意识

注重理解加减乘除运算的性质以及运算间的关系．

运算意识帮助学生理解加减乘除运算的意义，在问题解决情境中有意义地运用这些运算．《课程标准》强调在理解加减乘除运算的性质以及运算间的关系的基础上发展儿童的运算意识．与加、减法相关的运算意识发展是一~三年级关注的焦点，低年级学生通过计数、对数字的组合与分解的策略理解加、减法的含义．《课程标准》也在二年级要求学生探索乘法和除法的概念：乘法被看作是重复的加法；除法被看作是对数量的等分．与乘、除法相关的运算意识发展是四~六年级关注的焦点．理解运算的性质会帮助学生发展灵活的、有效的心算策略．而学生能够灵活地使用各种运算策略，表明他们具备较强的运算意识．《课程标准》在各年级均要求学生使用各种心算策略解决运算问题；鼓励学生使用学生设计、生成的算法和标准的算法，这有助于学生获得对运算的概念性理解．学生理解运算间的关系能提高他们的运算技能．学生在最初学习减法时，经常使用加、减法互为逆运算解决问题．在除法运算中也经常运用乘除法之间的逆运算关系解题．此外，《课程标准》将估算作为运算策略的一种，重视估算在发展各年级学生数感中所发挥的重要作用，强调学生在解决运算问题时，使用估算获得问题的近似解，判断答案的合理性．

2.4 比例关系

强调使用整数、小数和分数表征数量之间的乘法关系．

《课程标准》从四年级开始，增加比例关系为数感的组成元素．比例涉及到两个或更多相等的比．能理解比例关系，并根据比例关系进行推理是儿童数学思维的重大进展．比例关系是小学数学课程的顶点，为理解其它重要数学概念提供必要的基础和前提．例如：等值分数是分数学习中的重点和难点．“等值分数建立在两个量具有确定比例关系的基础上．”[11]理解比例关系会帮助学生实现分数、小数、百分数之间的转换．另一方面，比例推理是中学数学课程内容的基础[12]．也是科学、地理等其它学科的基础，在日常生活中有广泛的应用．

比例关系涉及到认识两个比之间的乘法关系．思考两个比之间的乘法关系是比例关系的基础．儿童在低年级就学习了两个量之间加法关系的比较（我有5个桔子，你有7个桔子，你比我多2个桔子）．儿童在最初接触比例关系时，可能进行两个量间的加法关系的比较．（例如认为1∶3=3∶5，因为每个比的两个数字的差都是2）因此，在乘法的情境中能区分乘法与加法被看作是比例推理的重要元素[13]．《课程标准》四年级要求使用整数描述两个量间的乘法关系，即用整数表示两个数量的比．五年级要求使用分数和小数描述两个量间的乘法关系，即用分数、小数表示两个数量的比．

3 对中国小学数学教育的启示

3.1 重视低年级儿童数感的发展

“数感发展的关键期是小学低年级．数感教学的重点应在第一学段．”[14]计数是儿童学习用数表示多少的第一步．计数降低了算术问题的难度，使它们能被儿童所接受．纵观中国的小学低年级数学教材，对计数的关注不多．“人教版”和“苏教版”一年级教材中的“数一数”并没有呈现多种计数模式和策略．只有“北师版”一年级教材中呈现灵活多样的计数策略：一个一个计数、两个两个计数、五个五个计数、十个十个计数，正向计数和反向计数相结合．因此建议在小学数学教材中适当增加计数的内容，扩展学生的计数模式，呈现灵活多样的计数策略，渗透加法和减法的意识，帮助学生理解数的本质和运算的意义．另一方面，教育工作者目前关注的重点是在学校数学或课堂教学中对学生数感的培养，而较少关注利用学生日常生活中的非正式经验发展儿童的数感．有研究表明：“儿童的数感很大程度上是在日常生活中的数学经验交流中获得的．”[15]因此需要将低年级的数学教学与日常生活的经验相联系，为学生提供计数的经验和机会．“让学生学会用自己的语言解释教学，用数学的语言去解释现实问题．”[16]例如：借助儿歌，故事，强调计数数字的顺序，既包含向前数又包含向后数．在爬楼梯的同时计数，建立计数的数字和步伐之间的一一对应关系；为学生创造参加游戏的机会，渗透计数策略，等等．

3.2 重视学生对运算的理解

“数感也是一种运用数字和运算法则进行灵活运算的能力，数字与计算之间的联系对学生形成数感具有重大的影响．”[17]对运算的理解，对运算知识、运算性质的把握与熟悉不仅是数感的重要组成部分，也是形成数感的基础[18]．而数感的发展又会促进运算能力的提升[19]．《义务教育数学课程标准（2011年版）》对数感的表述侧重于对数与数量、数量关系的意识、理解、领悟，对运算则仅仅强调感悟对运算结果的估计[20]．另一个核心概念运算能力关注的是根据法则和运算律正确地进行运算的能力[20]．综上可见对运算的理解关注不足．

在实际教学中，发展儿童对运算的概念性理解并没有受到普遍的关注．教材将运算的算法作为一系列的步骤、程序呈现给学生，而很少关注运算间的关系，很少关注儿童对运算基础概念的理解．例如，人教版小学数学教材在三年级上册讲授“有余数的除法”，教材首先关注的是标准的除法算式，整章的内容并没有将除法与乘法及减法相联系[21]．仅仅依靠记忆运算步骤的学生很少能使用数学推理解决问题．事实上，花费在促进运算的概念性理解上的时间并不会妨碍，甚至会提高运算的有效性．可以从如下方面提高学生对运算的理解：第一，理解运算间的关系．认识到加减乘除运算之间的相互联系能够帮助学生提高运算意识，促进对运算的深入理解，发展灵活的解题策略．在学生学习标准算法之前，他们应该有机会探索和发展各种策略和算法．当学生使用自己的策略解决问题时，他们发展对运算情境性的、概念性、程序性的理解．这帮助学生理解标准算法中程序、步骤的意义．第二，理解运算的性质．这会帮助学生发展灵活的、有效的心算策略．运算性质应该在问题解决的情境中引入和强调，不应该作为记忆的规则而被孤立地讲授．教师可以使用模型（具体的材料或图表、数轴）帮助学生将运算的性质可视化．例如可以将乘法分配率例如用图1所示的方格表征．

图1 乘法分配率的表征

3.3 进一步完善中国义务教育数学课程标准中的数感

数感在《全日制义务教育数学课程标准（实验稿）》以及《义务教育数学课程标准（2011年版）》中均作为核心概念被提出，由此可见数感是义务教育阶段数学课程内容的核心和聚焦点，是最应培养的数学素养之一，是促进学生发展的重要方面．为了帮助教师将学生数感的培养落实在数学教学过程中，那么对学生数感的发展与特征进行深入的研究，有清晰明确的认识是必要的前提条件．《义务教育数学课程标准（2011年版）》并没有界定数感的内涵，而是采用外延描述的方式，认为数感主要是指关于数与数量、数量关系、运算结果估计方面的感悟[20]．《义务教育数学课程标准（2011年版）解读》也从这3方面对数感进行了比较详尽的阐述．但是并没有分学段和年级，只是较为笼统地阐述了小学阶段这3方面的发展的特征、规律[22]．数感有一个后天的发展过程[23]．数感作为一种特殊的数学能力和数学素养，必然具有其自身发展的年龄特点，规律．有必要对数感进行进一步的深入的研究，尤其是进行量化的实证性的研究，分析探讨小学各年级或各学段的学生在数与数量、数量关系、运算结果估计3个方面发展的规律、特征，各年级或学段间在这3个方面是否存在显著性差异，是否存在发展的阶段性，是否存在性别差异等．根据各年级或各学段学生数感学习的特点，提出有针对性的教学策略，为教师的教学提供有价值的借鉴和参考．

[1] OECD2009. PISA 2009 Results: What Students Know and Can Do: Student Performance in Reading, Mathematics and Science (Volume I) [EB/OL]. http://www.oecd.org/pisa/pisaproducts/pisa2009/ pisa 2009 results what students know and can do student performance in reading mathematics and science volumei. htm

[2] OECD2012. PISA 2012 Results in Focus: What 15-year-olds Know and What They Can Do with What They Know [EB/OL]. http://www.oecd.org/pisa/keyfindings/pisa-2012-results-overview.pdf

[3] 张文宇，张守波．加拿大小学数学课程标准中的空间观念评析[J]．外国中小学教育，2013，（6）：53-58．

[4] Ontario Ministry of Education.[M]. Toronto: Author. 2005.

Target population:healthy people aged between 20 and 70 in universities,enterprises,institutions and communities in Beijing.

[5] 史宁中．数学思想概论——数量与数量关系的抽象[M]．长春：东北师范大学出版社，2008．

[6] Threfall J, Frobisher L. Patterns in Processing and Learning Addition Facts [A]. In: Orton A.[C]. London: Cassell, 1999.

[7] Ginsburg H P. Mathematics Learning Disabilites: A View from Developmental Psychology [J]., 1997, 30(1): 20-33.

[8] Geary D C, Hoard M K, Hamson C O. Numerical and Arithmetical Cognition: Patterns of Functions and Deficits in Children at Risk for a Mathematical Disability [J]., 1999, 74(3): 213-239.

[9] Geary D C. Learning Disabilities in Arithmetic: Problem Solving Differences and Cognitive Deficits [A]. In: Swanson H L, Harris K, Graham S.[C]. New York: Guilford Publishers , 2003.

[10]  Nancy C Jordan, David Kaplan. Number Sense Growth in Kindergarten: A Longitudinal Investigation of Children at Risk for Mathematics Difficulties [J]., 2006, 77(1): 153-175.

[11] 韩玉蕾，辛自强，胡清芬．等值分数概念的理解[J]．心理发展与教育，2012，（2）：210-217．

[13]  Van Dooren W, De Bock D, Hessels A, et al. Not Everything is Proportional: Effects of Age and Problem Type on Propensities for Overgeneralization [J]., 2005, 23(1): 57-86.

[14] 史宁中，吕世虎．对数感及其教学的思考[J]．数学教育学报，2006，15（2）：9-11．

[15] 浦晓黎．国外学前儿童数感研究综述[J]．幼儿教育（教育科学版），2006，（10）：41-46．

[16] 叶蓓蓓．对数感的再认识与思考[J]．数学教育学报，2004，13（2）：34-36．

[17] 徐文彬，喻平．“数感”及其形成与发展[J]．数学教育学报，2007，16（2）：8-11．

[18] 陆珺．国内数感研究综述[J]．课程·教材·教法，2009，（6）：46-50．

[19] 马云鹏，史炳星．认识数感与发展数感[J]．数学教育学报，2002，11（2）：46-49．

[20] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[21] 课程教材研究所小学数学课程教材研究开发中心．义务教育课程标准实验教材数学（三年级上册）[M]．北京：人民教育出版社，2009．

[22] 教育部基础教育课程教材专家工作委员会．义务教育数学课程标准（2011年版）解读[M]．北京：北京师范大学出版社，2012．

[23] 郑毓信．《数学课程标准（2011）》的“另类解读”[J]．数学教育学报，2013，22（1）：1-7．

附录：数感与运算能力的课程期望

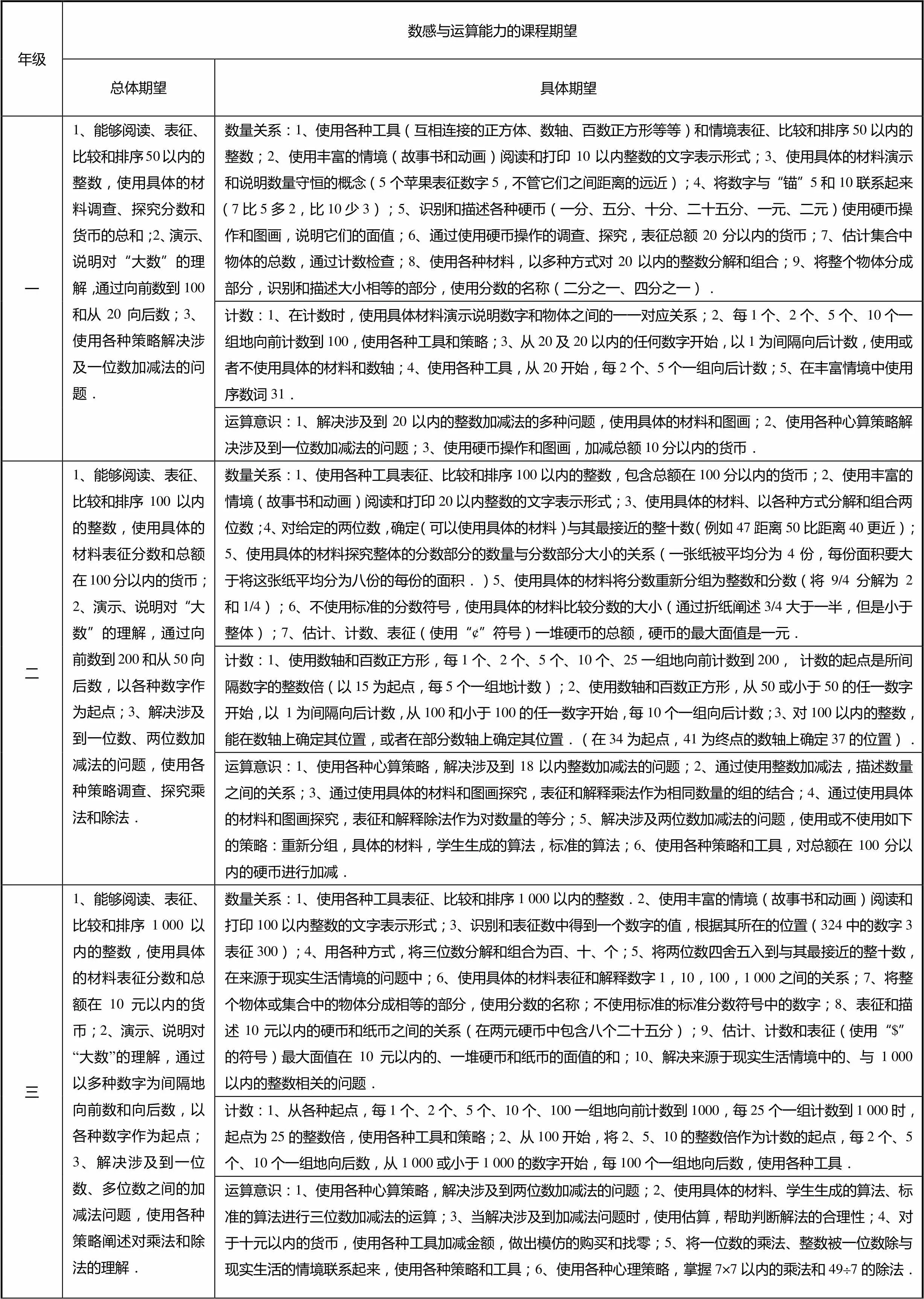
年级数感与运算能力的课程期望 总体期望具体期望 一1、能够阅读、表征、比较和排序50以内的整数，使用具体的材料调查、探究分数和货币的总和；2、演示、说明对“大数”的理解，通过向前数到100和从20向后数；3、使用各种策略解决涉及一位数加减法的问题．数量关系：1、使用各种工具（互相连接的正方体、数轴、百数正方形等等）和情境表征、比较和排序50以内的整数；2、使用丰富的情境（故事书和动画）阅读和打印10以内整数的文字表示形式；3、使用具体的材料演示和说明数量守恒的概念（5个苹果表征数字5，不管它们之间距离的远近）；4、将数字与“锚”5和10联系起来（7比5多2，比10少3）；5、识别和描述各种硬币（一分、五分、十分、二十五分、一元、二元）使用硬币操作和图画，说明它们的面值；6、通过使用硬币操作的调查、探究，表征总额20分以内的货币；7、估计集合中物体的总数，通过计数检查；8、使用各种材料，以多种方式对20以内的整数分解和组合；9、将整个物体分成部分，识别和描述大小相等的部分，使用分数的名称（二分之一、四分之一）． 计数：1、在计数时，使用具体材料演示说明数字和物体之间的一一对应关系；2、每1个、2个、5个、10个一组地向前计数到100，使用各种工具和策略；3、从20及20以内的任何数字开始，以1为间隔向后计数，使用或者不使用具体的材料和数轴；4、使用各种工具，从20开始，每2个、5个一组向后计数；5、在丰富情境中使用序数词31． 运算意识：1、解决涉及到20以内的整数加减法的多种问题，使用具体的材料和图画；2、使用各种心算策略解决涉及到一位数加减法的问题；3、使用硬币操作和图画，加减总额10分以内的货币． 二1、能够阅读、表征、比较和排序100以内的整数，使用具体的材料表征分数和总额在100分以内的货币；2、演示、说明对“大数”的理解，通过向前数到200和从50向后数，以各种数字作为起点；3、解决涉及到一位数、两位数加减法的问题，使用各种策略调查、探究乘法和除法．数量关系：1、使用各种工具表征、比较和排序100以内的整数，包含总额在100分以内的货币；2、使用丰富的情境（故事书和动画）阅读和打印20以内整数的文字表示形式；3、使用具体的材料、以各种方式分解和组合两位数；4、对给定的两位数，确定（可以使用具体的材料）与其最接近的整十数（例如47距离50比距离40更近）；5、使用具体的材料探究整体的分数部分的数量与分数部分大小的关系（一张纸被平均分为4份，每份面积要大于将这张纸平均分为八份的每份的面积．）5、使用具体的材料将分数重新分组为整数和分数（将9/4分解为2和1/4）；6、不使用标准的分数符号，使用具体的材料比较分数的大小（通过折纸阐述3/4大于一半，但是小于整体）；7、估计、计数、表征（使用“¢”符号）一堆硬币的总额，硬币的最大面值是一元． 计数：1、使用数轴和百数正方形，每1个、2个、5个、10个、25一组地向前计数到200，计数的起点是所间隔数字的整数倍（以15为起点，每5个一组地计数）；2、使用数轴和百数正方形，从50或小于50的任一数字开始，以 1为间隔向后计数，从100和小于100的任一数字开始，每10个一组向后计数；3、对100以内的整数，能在数轴上确定其位置，或者在部分数轴上确定其位置．（在34为起点，41为终点的数轴上确定37的位置）． 运算意识：1、使用各种心算策略，解决涉及到18以内整数加减法的问题；2、通过使用整数加减法，描述数量之间的关系；3、通过使用具体的材料和图画探究，表征和解释乘法作为相同数量的组的结合；4、通过使用具体的材料和图画探究，表征和解释除法作为对数量的等分；5、解决涉及两位数加减法的问题，使用或不使用如下的策略：重新分组，具体的材料，学生生成的算法，标准的算法；6、使用各种策略和工具，对总额在100分以内的硬币进行加减． 三1、能够阅读、表征、比较和排序1 000以内的整数，使用具体的材料表征分数和总额在10元以内的货币；2、演示、说明对“大数”的理解，通过以多种数字为间隔地向前数和向后数，以各种数字作为起点；3、解决涉及到一位数、多位数之间的加减法问题，使用各种策略阐述对乘法和除法的理解．数量关系：1、使用各种工具表征、比较和排序1 000以内的整数．2、使用丰富的情境（故事书和动画）阅读和打印100以内整数的文字表示形式；3、识别和表征数中得到一个数字的值，根据其所在的位置（324中的数字3表征300）；4、用各种方式，将三位数分解和组合为百、十、个；5、将两位数四舍五入到与其最接近的整十数，在来源于现实生活情境的问题中；6、使用具体的材料表征和解释数字1，10，100，1 000之间的关系；7、将整个物体或集合中的物体分成相等的部分，使用分数的名称；不使用标准的标准分数符号中的数字；8、表征和描述10元以内的硬币和纸币之间的关系（在两元硬币中包含八个二十五分）；9、估计、计数和表征（使用“$”的符号）最大面值在10元以内的、一堆硬币和纸币的面值的和；10、解决来源于现实生活情境中的、与1 000以内的整数相关的问题． 计数：1、从各种起点，每1个、2个、5个、10个、100一组地向前计数到1000，每25个一组计数到1 000时，起点为25的整数倍，使用各种工具和策略；2、从100开始，将2、5、10的整数倍作为计数的起点，每2个、5个、10个一组地向后数，从1 000或小于1 000的数字开始，每100个一组地向后数，使用各种工具． 运算意识：1、使用各种心算策略，解决涉及到两位数加减法的问题；2、使用具体的材料、学生生成的算法、标准的算法进行三位数加减法的运算；3、当解决涉及到加减法问题时，使用估算，帮助判断解法的合理性；4、对于十元以内的货币，使用各种工具加减金额，做出模仿的购买和找零；5、将一位数的乘法、整数被一位数除与现实生活的情境联系起来，使用各种策略和工具；6、使用各种心理策略，掌握7×7以内的乘法和49¸7的除法． 四1、能够阅读、表征、比较和排序10 000以内的整数、十分位的小数、简单的分数、总额在100元以内的货币；2、阐述对“大数”的理解，通过向前数和向后数，以0.1和分数为单位；3、解决涉及一位整数和多位整数的四则运算问题，涉及到十分位小数的加减法问题，使用各种策略；4、说明和演示对于比例推理的理解，通过探究整数的单位比例．数量关系：1、表征、标记和排序10 000以内的整数，使用各种工具；2、对于从0.1到10 000的小数和整数，阐述对位置值的理解，使用各种工具和策略；3、使用丰富的情境（故事书和动画）阅读和打印1 000以内整数的文字表示形式；4、将四位数四舍五入到与其最接近的十位、百位、千位，在来源于现实生活情境的问题中；5、表征、比较、排序十分位的小数，使用各种工具；6、使用具体的材料、文字和标准的分数符号表征分数，解释分母与分子的含义；7、对分子相同或分母相同的分数比较和排序；8、将分数与基准数字0、1/2、1比较大小；8、阐述和解释等值分数之间的关系，使用具体的材料；9、阅读和表征100元以内的加拿大货币；10、解决来源于现实生活情境中的、与10 000以内的整数相关的问题． 计数：1、使用具体的材料和数轴，以1/2、1/3、1/4、1/10为单位向前数，超过1；2、使用具体的材料和数轴，以十分位的任一小数为起点，以1/10为单位向后数． 运算意识：1、使用各种心算策略，解决两位数的加减法；2、解决涉及四位数加减法问题，使用学生生成的算法和标准的算法；3、十分位小数的加减法，使用具体的材料、学生生成的算法；4、对于一百元以内的货币，使用各种工具加减金额，做出模仿的购买和找零；5、使用各种心算策略，计算9×9以内的乘法和81¸9的除法；6、使用各种心算策略，解决涉及到的一位数的乘法问题；7、使用心算策略，计算整数乘以10、100、1 000，整数被10、100除；8、计算两位数乘以一位数，使用各种工具、学生生成的算法、标准的算法；9、计算两位数除以一位数；10、当解决涉及到整数的加减乘法运算时，使用估算，判断答案的合理性． 比例关系：1、描述涉及到的简单的整数乘法关系；2、通过探究、确定和解释分数与十分位小数之间的关系，使用各种工具和策略；3、阐述对涉及到的单位比例的、简单乘法关系的理解，使用具体的材料和图画． 五1、能够阅读、表征、比较和排序100 000以内的整数、百分位的小数、真分数、假分数、带分数；2、阐述对“大数”的理解，通过向前数和向后数，以0.01为单位；3、解决涉及多位整数的乘法和除法问题，百分位小数的加减法问题，使用一系列的策略；4、阐述对比例推理的理解，通过探究整数的比率．数量关系：1、表征、比较和排序从0.01到100 000的小数和整数；2、对于从0.01到100 000的小数和整数，阐述对位置值的理解，使用各种工具和策略；3、使用丰富的情境（故事书和动画）阅读和打印10 000以内整数的文字表示形式；4、将小数四舍五入到十分位，在来源于现实生活情境的问题中；5、对于同分母分数表征、比较和排序、使用一系列工具、使用标准的分数符号；6、阐述和解释等值分数的概念，使用具体的材料；7、阐述和解释小数的等价表示，使用具体的材料和图画；8、、阅读和表征1 000元以内的加拿大货币；9、解决来源于现实生活情境中的、与100 000以内的整数相关的问题． 计数：以任一小数为起点，以0.01为单位向前数，使用具体的材料和数轴． 运算意识：1、使用心算策略，解决涉及的整数的加减乘除问题；2、百分位小数的加减法，包含金钱总数，使用具体的材料，估算，和算法；3、两位数乘以两位数，使用估算，学生生成的算法和标准算法；4、三位数除以一位数，使用估算，学生生成的算法和标准算法；5、小数乘以10、100、1 000，小数除以10、100，使用心算策略；6、使用估算，当解决设计整数的加减乘除运算时，帮助判断答案的合理性． 比例关系：1、描述数量之间的乘法关系，通过使用简单的分数和小数；2、通过使用具体材料、图画、计算器探究，确定和解释分数与它的等值小数形式；3、阐述对简单乘法关系的理解，涉及到整数比率，通过使用具体材料和图画进行探究． 六1、能够阅读、表征、比较和排序1 000 000以内的整数、千分位的小数、真分数、假分数、带分数；2、解决涉及整数乘除法的问题，千分位小数的加减法问题，使用一系列的策略；3、阐述对百分比，比和单位比率关系的理解．数量关系：1、表征、比较和排序从0.001到1 000 000的小数和整数；2、对于从0.001到1 000 000的小数和整数，阐述对位置值的理解，使用各种工具和策略；3、使用丰富的情境（故事书和动画）阅读和打印100000以内整数的文字表示形式；4、对于分母不同的分数（包含真分数假分数和带分数）能够表征、比较和排序，使用一系列的策略，使用标准的分数符号；5、以10%，25%，50%，75%，100%为基准数字，估计数量的大小；6、解决来源于现实生活情境中的、与1 000 000以内的整数相关的问题；7、确定合数和质数，解释他们之间的关系． 运算意识：1、使用各种心算策略解决整数的加减乘除问题；2、解决涉及四位数与两位数之间的乘除法，使用一系列的工具和策略；3、解决千分位小数的加减法，使用具体的材料、估算、算法和计算器；4、整数与十分位小数间的乘除法，使用具体的材料、估算、算法和计算器；5、整数乘以0.1、0.01、0.01，使用心算策略；6、小数乘以或除以10，100，1 000和10 000，使用心算策略；7、当解决涉及整数、小数的加减法问题时，使用估算，帮助判断答案的合理性；8、解释实施运算标准顺序的需要，探究进行一系列运算时，改变顺序对结果的影响． 比例关系：1、表征现实生活中发现的比，使用具体的材料，图画和标准的分数符号；2、通过使用具体的材料、图画、计算器去探究，确定和解释分数、小数和百分数之间的关系；3、通过使用单位价格表征关系．

Review on Number Sense and Numeration in Canada Primary Mathematics Curriculum Standards——Taking Province of Ontario as an Example

ZHANG Wen-yu1, SONG Jun2

(1. College of Education and Physical Education, Bohai University, Liaoning Jinzhou 121013, China; 2. Crane Township Primary School, Liaoning Panjin 124000, China)

. In 2005, Ontario ministry of education publishedNumber sense and numeration are viewed as the foundation of other Strands. First, the big ideas of Number sense and numeration are introduced; then analyzes characteristics. These features Provide some references for research on curriculum and construction in primary mathematics

number sense and numeration; quantity relationships; counting; operational sense; proportional relationships

[责任编校：周学智]

G40-059.3

A

1004–9894（2016）03–0038–06

2016–02–10

辽宁省教育科学“十二五”规划项目——基于CBAM模式的初中数学课程改革实施研究（JG14CB010）；辽宁省社会科学规划基金项目——辽宁省少数民族基础教育现状调查与对策研究（L12DMZ012）；辽宁省教育厅一般项目——基础教育课程改革背景下的小学数学教材国际比较研究（W2013161）

张文宇（1980—），男，辽宁朝阳人，副教授，教育学博士，主要从事数学课程与教学论研究．