基于并行策略的热固耦合多材料柔顺机构设计*

张宪民 胡凯 王念峰 郭浩

(华南理工大学 机械与汽车工程学院∥广东省精密装备与制造技术重点实验室, 广东 广州 510640)

基于并行策略的热固耦合多材料柔顺机构设计*

张宪民 胡凯 王念峰†郭浩

(华南理工大学 机械与汽车工程学院∥广东省精密装备与制造技术重点实验室, 广东 广州 510640)

热效应在结构设计领域受到广泛的重视，文中利用拓扑优化的方法，对热驱动柔顺机构设计进行了研究，提出了相应的基于并行策略的求解模型.该模型的核心是将一个复杂的多材料热固耦合问题离散成为单材料热固耦合子问题，然后对这些子问题并行求解，并根据整体目标的需要，对所有子问题的解进行调整以得到原始问题的解.对所有的单材料子问题，基于SIMP(固体各向同性材料惩罚模型)材料插值模型，建立了热固耦合拓扑优化求解模型，然后利用顺序耦合方法进行热-结构多物理场耦合分析，独立并行求解.该模型在理论和实践上都比较简单，可以处理任意多种材料，并且可以避免零碎的拓扑结构，因而有利于制造.文中还通过数值算例说明了此方法的有效性.

拓扑优化；柔顺机构；热固耦合；敏度分析

拓扑优化一直是结构优化领域的热点问题，采用拓扑优化的方法设计柔顺机构具有较大的设计自由度，因而受到人们的重视[1- 5].常用的拓扑优化设计方法主要有变密度法[6- 8]、基础结构法[9- 10]、水平集法[11- 12]等.

多场耦合是指在一个系统中，热、电、磁和结构场等相互作用和影响的现象，多场耦合下的结构拓扑关系比较复杂，与直观感觉和经验相差较大，需要一种能够综合考虑多场关系来设计结构布局形式的方法，因而涉及耦合场结构分析的拓扑优化应用研究成为一个重要的发展方向[13].Sigmund[14- 15]研究了电热场耦合下的双材料插值模型问题和驱动器的拓扑优化建模、设计和制造问题；李冬梅等[16]将可靠性分析用于热固耦合拓扑优化中，提出了一种基于概率约束的可靠性拓扑优化设计方法；Takezawa等[17- 18]研究了拓扑优化中结构强度和热传导约束问题，在优化的后续阶段采用PFM法更新密度函数，从而避免中间密度单元，得到清晰的结构边界；Koga等[19]采用拓扑优化的方法，在稳态热模型中综合考虑传导和强制热对流的影响，设计了完整的循环对流性能最佳的散热器.然而迄今为止，基于多材料的多场耦合问题的研究相对较少，尚有待深入研究.

在给定约束条件和负载下，以一定的设计目标，寻求多种材料在设计域内的最优分布，即为多材料的拓扑优化.相比于单材料机构，多材料机构能够充分发挥各种材料的优良属性，拥有更大的设计自由度，受到了许多的关注与研究.Guo等[20]提出基于水平集的变分一致策略，研究了应力约束下多材料拓扑优化问题；Wang等[21]提出了基于水平集的多材料拓扑优化模型，每一相材料由不同的水平集函数组合而成，优化得到光滑的边界和清晰的表面结构；Tavakoli[22]基于多相体积约束的金兹堡-朗道能量泛函，提出一种解决多材料拓扑优化问题的模型，采用分步投影的最速下降法对设计变量进行更新.上述情形中没有涉及多材料与多场耦合组合拓扑优化的问题，同时对机构及耦合驱动也尚未有深入的研究.

文中重点研究了多材料柔顺机构的热固耦合拓扑优化问题.首先，将原始的多材料多场耦合优化问题按照材料的种类离散成单材料多场耦合优化子问题；其次，对所有的单材料子问题，基于SIMP(固体各向同性材料惩罚模型)建立了热固耦合拓扑优化模型，利用顺序耦合方法进行热-结构多物理场耦合分析，独立并行求解；接着调整所有子问题的解以得到符合原始的多场耦合问题的解；最后通过算例对所提方法的有效性进行了验证.

1 材料插值模型及并行优化策略

1.1 基于SIMP模型的变密度法

各向同性材料的SIMP法又称变密度法，其基本思想为：设计域被离散成为微结构单元，设计变量定义为离散单元的相对密度，可取0到1之间任意值.单元的材料属性，比如杨氏模量与单元相对密度呈指数变化关系.设E0为材料原始的弹性模量，E是单元相对密度值等于xe时的弹性模量值，则存在关系式：

E=(xe)pE0

(1)

其中，p为惩罚因子，其目的在于对中间密度单元项进行惩罚，以尽量减少结构中间密度单元的数目，使结构单元密度尽可能靠近1或0两极.通常p取值大于3[14].

1.2 并行优化策略

由于原始的问题为多材料多场耦合拓扑优化问题，当按照材料的种类离散为单材料子问题后，所有的子问题都成为单材料多场耦合问题.对于单材料多场耦合拓扑优化问题，国内外学者已经做了许多研究[23- 24].文中提出一种并行优化策略，作为一种用于同时解决多材料的多场耦合问题的新方法.

所谓并行优化，就是对所有的单材料子问题独立并行求解.不难看出，这种优化策略的核心与难点在于后续如何统筹所有子问题的解，以得到原始优化问题的解.

(2)

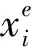
2 热固耦合理论分析与建模

2.1 耦合场有限元分析

耦合场分析是指在有限元分析的过程中综合考虑了多种物理场的交叉作用和相互影响.常见的耦合分析方法有直接耦合与间接耦合方法[13].文中采用间接耦合中的顺序耦合分析方法，首先进行热场有限元分析，计算得到热场作用下的温度分布矩阵，然后将热分析得到的节点温度用于计算热载荷，作为体力施加给弹性场，最后求解热载荷驱动下的结构响应.

根据SIMP模型，单元材料的属性值依赖单元相对密度值，热和结构耦合系统可以用下面两个有限元方程描述：

(3)

其中：x=(x1,x2,...,xM),表示多种材料相对密度向量；K1表示热刚度矩阵；K2表示结构刚度矩阵；U1为温度向量；U2为位移矢量；P1、P2分别为热载荷向量和结构外载荷矢量.

2.2 耦合场的敏度分析

基于SIMP法的优化问题采用基于梯度算法更新设计变量，因而需要求解结构响应对设计变量的敏度信息.敏度分析一般有3种方法：直接法、半解析法和伴随矩阵法.此处采用伴随矩阵法求解目标函数对各种材料设计变量的敏度.

对于一个热固耦合柔顺机构的优化问题可描述为

(4)

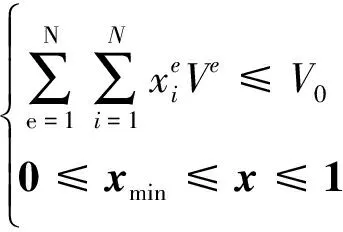
其中Ve和V0分别为单元体积和最大许用体积,xmin是最小允许相对密度值向量.结构响应规定为给定点的输出位移uout，可写为

uout=LTU2

(5)

LT是一个矢量，除了输出自由度方向的值为1，其他分量全部为0.假定有限元方程(3)已经求得，则式(5)可重写为

(6)

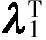
(7)

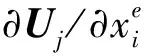
(8)

这可以通过设置如下伴随向量的值实现：

(9)

(10)

目前适用于拓扑优化的算法主要有优化准则法和数学规划算法两大类[25]，文中采用优化准则算法对设计变量进行求解更新.它是一种简单方便、收敛迅速的算法，非常适合于文中并行求解单材料子问题.采用SIMP模型求解的过程中，不可避免地会出现棋盘格现象，文中采用Sigmund[26]提出的敏度过滤技术抑制棋盘格式问题.

3 设计变量并行更新

当单材料子问题全部求解之后，得到包含M种单材料的解向量xi.按照前述的SIMP模型，在一个单元中，密度值是一个0到1之间的连续值.则对于一个多材料问题，任意种材料均可在任意单元存在，则单元密度之和可能超过1，这种单元称为过饱和单元.显然，这种单元的存在违背了SIMP模型的原理.出于对模型有效性的考虑，需要对过饱和单元进行处理，从而保证所有的单元密度之和均不超过1.此处为每种材料预先设定一个优先级，优先级最低的材料最先从过饱和单元中去除，假设材料的优先级顺序为S1,S2,…,SM(从高到低)，调整后的过饱和单元密度值为

(11)

需要注意的是，这里处理过饱和单元的过程是一个人工选择的过程.它根据人为设定的方法确定出优先度顺序对过饱和单元的材料进行取舍.这种更新方法的流程如图1所示.

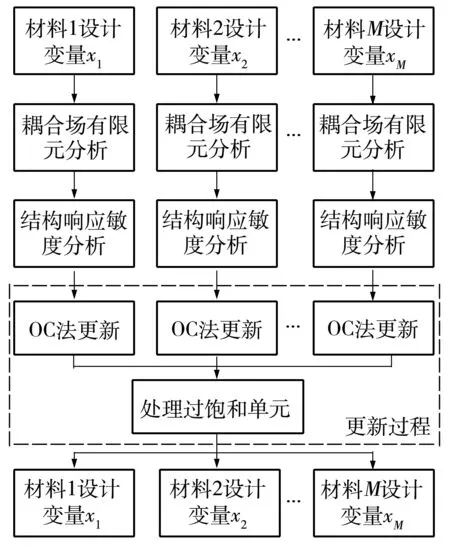
图1 设计变量更新流程

该方案是基于单材料拓扑优化的理论研究提出的，其本质是通过特殊策略将多材料问题分解为多种材料对应的单材料子问题进行更新，并保证设计结果的可行性.因此，该方案下除了可以使用擅长处理复杂约束问题的移动渐近线法等进行更新外，还可以使用对简单约束问题具有较优收敛结果以及速度的优化准则法进行更新，从而使得多材料拓扑优化问题的解决效率得到提高.此外，这种方案的执行过程具有很高的分立性与并行性，因此可以很容易地扩展到更多种材料的拓扑优化问题.

文中的收敛准则定义为任意种材料的设计变量最后相邻两步的改变量不大于某一极小值.假定迭代进行了t步，修正后的设计变量的t-1与t步之间最大差值为

ε=max|(xi)t-(xi)t-1|

(12)

其中,ε是收敛算子，通常取ε≤0.01.

4 数值算例及讨论

本节选取几个基于多材料多场耦合拓扑优化的的例子，说明前述理论模型的有效性.为不失一般性，在给出双材料拓扑结果之后，三材料的例子也已给出.设计域内温度向量为恒量，所有算例均不施加外在负载，只需要考虑纯热驱动下柔顺机构的设计问题.

4.1 双材料热驱动器

本例(算例1)采用一个比较常见的热驱动器作为优化对象，两种材料的设计参数初始值如表 1所示.设计域与边界条件如图2所示，上、下、左3个壁均绝热，在右边中间区域获得位移输出.由于对称性，只需要对上半部分进行优化就可得到整体机构结果.图3(a)-3(d)分别为两种材料(红：绿)体积比为5∶1的热驱动器设计中间结果，图3(e)、图4分别为热驱动器最终结果以及优化迭代曲线.

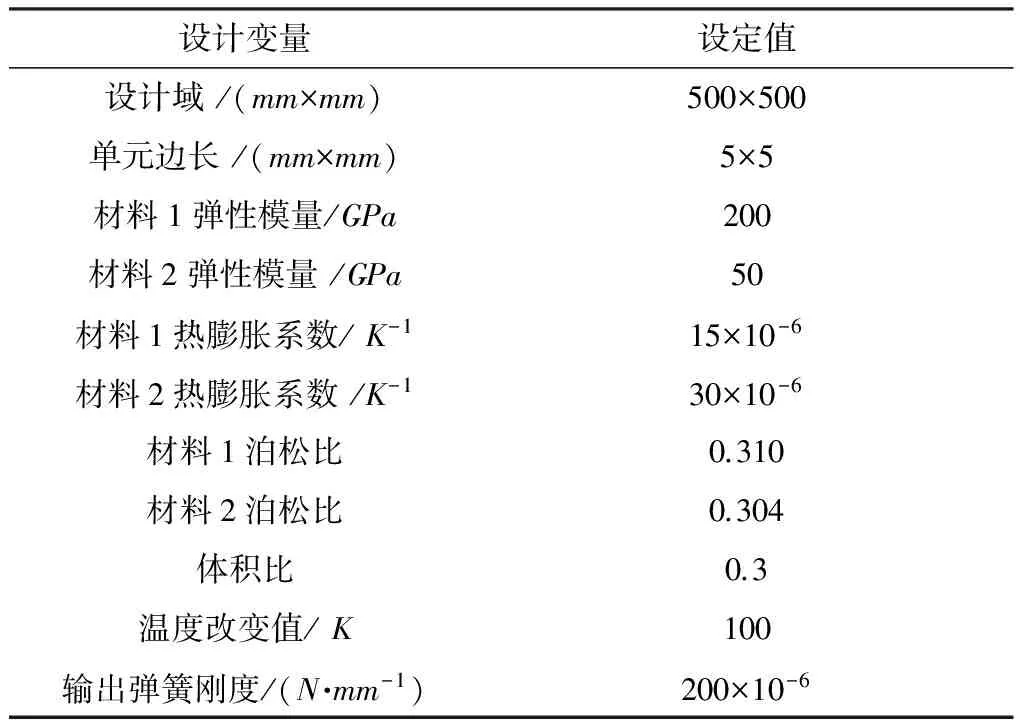
表 1 设计参数初始值(算例1)

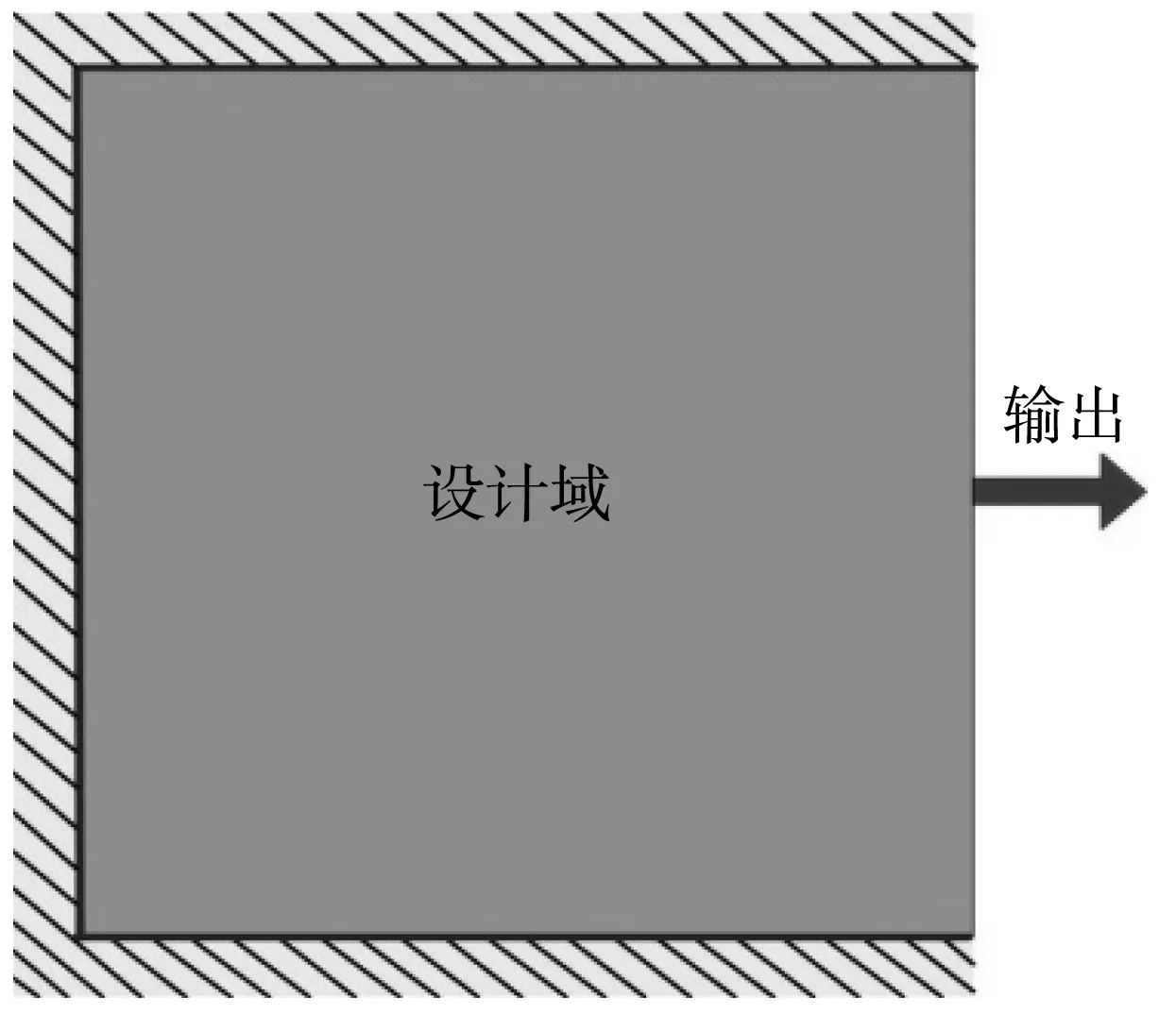
图2 热驱动器设计域及边界条件(算例1)

Fig.2 Design domain and boundary conditions of heat actuator (Example 1)

图3 热驱动器设计结果(算例1)

图4 对应图3中热驱动器的优化收敛曲线

Fig.4 Conversion history of heat actuator corresponding to Fig.3

观察图3最终的拓扑结果，可以发现使用文中提出的多材料设计方法得到的机构分块明显而独立，从制造的角度看非常适用，可以先分块制造，再使用搭接等连接技术连接成一体以生产.

4.2 有约束区域的双材料热驱动器

本例(算例2)设计一个材料分布区域受到限制的双材料热驱动器，设计域与边界条件如图5所示，设计域中间区域作为主动受热驱动材料分布区，禁止被驱动材料存在，而周围区域作为受动材料分布区，禁止主动材料存在，同时结构上、下两侧允许水平方向移动.两种材料的设计参数初始值与算例1相同，其中中间限制区域的大小为34 mm×34 mm.图6(a)、图7(a)分别为两种材料的体积比均为5∶1的热驱动器设计结果以及目标函数收敛曲线；图6(b)、图7(b)分别为两种材料(红∶绿)体积比分别为2∶1的热驱动器设计结果以及收敛曲线.

图5 热驱动器设计域及边界条件(算例2)

Fig.5 Design domain and boundary conditions of heat actuator (Example 2)

同样，从图6中的设计结果可以看出，两种材料边界清晰，分块独立.通过迭代曲线不难发现，优化迭代过程收敛稳定，说明对于复杂的多材料和多场耦合组合优化问题，文中所提出的方法具有较好的鲁棒性.

图6 热驱动器不同约束下的设计结果(算例2)

Fig.6 Design result of heat actuators under different constraints(Example 2)

Fig.7 Conversion history of heat actuators corresponding to Fig.6

4.3 三材料热驱动器

为不失一般性，此处(算例3)用一个三材料的热驱动器说明方法的有效性.其设计域和边界条件与算例1相同，3种材料的设计参数初始值如表 2所示，其他参数与之前算例相同.图8(a)、图9(a)为3种材料体积比为4∶1∶1的热驱动器设计结果及收敛曲线；图8(b)、 图9(b)为3种材料体积分别为10∶1∶1的热驱动器设计结果及收敛曲线.

图8 三材料热驱动器不同约束下的设计结果

Fig.8 Design result of three-materials heat actuators under different constraints

表2 设计参数初始值(算例3)

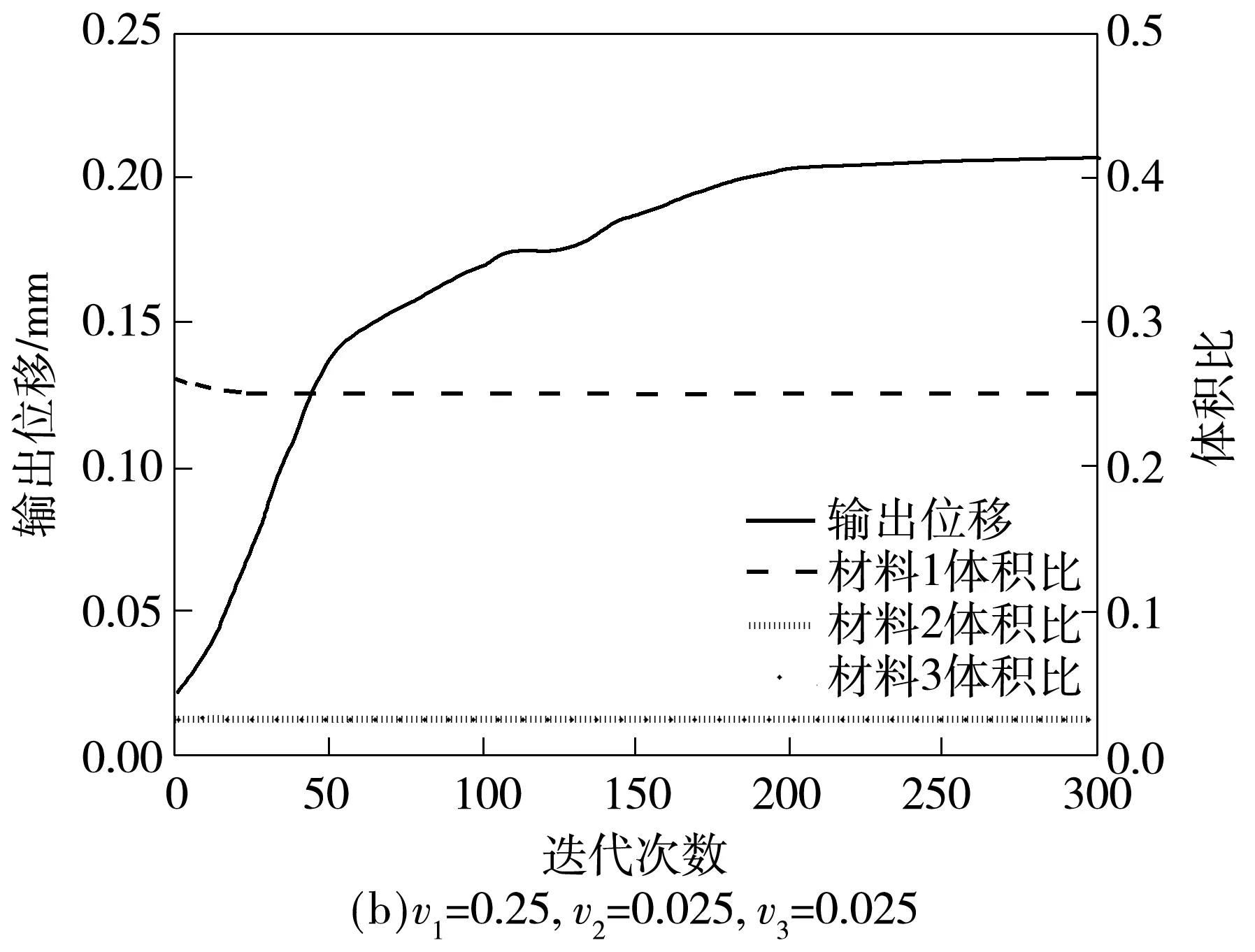
图9 三材料热驱动器对应图8中设计结果的收敛曲线

Fig.9 Conversion history of three-materials heat actuators in Fig.8

从图8的设计结果可以看到，优化三材料热驱动柔顺机构时，依然能够得到比较理想的拓扑结构，各材料之间边界清晰，分块独立.这说明基于并行优化策略的模型能够突破传统的双材料限制，进行真正意义上的任意多种材料的拓扑优化设计.

5 结论

(1)提出了一种新的基于多材料设计多场耦合柔顺机构的求解方法.将复杂的多材料问题离散为简单的单材料子问题，然后并行独立求解.

(2)基于刚度可加性理论，得到了全局刚度矩阵与各材料之间呈线性关系，并将之推广至其他耦合物理场.

(3)该方法在理论和应用上都比较简单，并且能够处理任意多种材料.数值算例表明，新方法设计的机构合理，各材料之间分块明显，利于加工，因而方法是有效的.

(4)重点研究了多场耦合中的热固耦合效应，为后续的热、电、结构场耦合理论分析和研究提供了极为重要的参考价值.

(5)算例部分只给出了依靠纯热驱动作用下的柔顺机构设计与分析，表明热效应对结构变形的巨大影响.需要说明的是，对于已有较多的外力和热场同时作用下的结构分析，文中所提方法也是有效的，热载荷与外力同时作用下的情形类似于多输入柔顺机构设计；其次，并行优化策略尚未在数学上得到严格证明，也无法说明优化的结果是全局最优的，但是大量的算例证明了该方法的有效性.

[1] 张宪民.柔顺机构拓扑优化设计 [J].机械工程学报,2003,39(11)：47- 51. ZHANG Xian-min.Topology optimozation of compliant mechanisms [J].Chinese Journal of Mechanical Engineering,2003,39(11)：47- 51.

[2] HAO G.Towards the design of monolithic decoupled XYZ compliant parallel mechanisms for multi-function applications [J].Mechanical Sciences,2013,4：291- 302.

[3] 于靖军,宗光华,毕树生.全柔性机构与MEMS [J].光学精密工程,2001,9(1):1- 5. YU,Jing-jun,ZONG Guang-hua,BI Shu-sheng.Fully compliant mechanisms and MEMS [J].Opt Precis Eng,2001,9(1)：1- 5.

[4] 陈贵敏,李端玲.平面柔顺机构的自由度 [J].机械工程学报,2010,46(13)：48- 53. CHEN Gui-min,LI Duan-ling.Degree of freedom of planar compliant mechanisms [J].Journal of Mechanical Engineering,2010,46(13)：48- 53.

[5] ROZVANY G I N.A critical review of established methods of structural topology optimization [J].Structural and Multidisciplinary Optimization,2009,37(3)：217- 237.

[6] SIGMUND O.On the design of compliant mechanisms using topology optimization [J].Journal of Structural Mechanics,1997,25(4)：493- 524.

[7] 罗震,蒙永立,郭文德,等.分布式柔性机构拓扑优化设计的理论和算法 [J].机械工程学报,2006,42(10)：27- 36. LUO Zhen,MENG Yong-li,GUO Wen-de,et al.Theoretical and algorithmic on topology optimization design of distributed compliant mechanisms [J].Chinese Journal of Mechanical Engineering,2006,42(10)：27- 36.

[8] BRUNS T E.A revaluation of the SIMP method with filtering and an alternative formulation for solid-void topology optimization [J].Structural and Multidisciplinary Optimization,2005,30(6)：428- 436.

[9] RAMRAKHYANI D S,FRECKER M I,LESIEUTRE G A.Hinged beam elements for the topology design of compliant mechanisms using the ground structure approach [J].Structural and Multidisciplinary Optimization,2009,37(6)：557- 567.

[10] WANG Nian-feng,ZHANG Xian-min.Multi-material topology optimization of complaint mechanism using ground structure approach [C]∥Proceedings of International Conference on Manipulation,Manufacturing and Measurement on the Nanoscale(3M-NANO).[S.l.]：IEEE,2014：249- 254.

[11] ZHU Ben-liang,ZHANG Xian-min,WANG Nian-feng.Topology optimization of hinge-free compliant mechanisms with multiple outputs using level set method [J].Structural and Multidisciplinary Optimization,2013,47(5)：659- 672.

[12] 罗俊召,陈立平,罗震.基于半隐式格式的水平集法连续体结构形状和拓扑优化方法 [J].固体力学学报,2008,29(2)：175- 180. LUO Jun-zhao,CHEN Li-ping,LUO Zhen.A level set method for topology optimization using AOS scheme [J].Chinese Journal of Solid Mechanics,2008,29(2)：175- 180.

[13] 李冬梅.多场耦合及多相材料的柔顺机构拓扑优化研究 [D].广州：华南理工大学,2011.

[14] SIGMUND O.Design of multi-physics actuators using topology optimization(Part I)：one-material structures [J].Computer Methods in Applied Mechanics and Engineering,2001,190(49)：6577- 6604.

[15] SIGMUND O.Design of multi-physics actuators using topology optimization(Part II)：Two-material structures [J].Computer Methods in Applied Mechanics and Engineering,2001,190(49)：6605- 6627.

[16] 李冬梅,张宪民,王念峰,等.基于可靠性约束的热固耦合结构拓扑优化 [J].华南理工大学学报(自然科学版),2011,39(6)：42- 46. LI Dong-mei,ZHANG Xian-min,WANG Nian-feng,et al.Topology optimization of thermo-mechanical coupling structures based on reliability constraint [J].Journal of South China University of Technology(Natural Science Edition),2011,39(6)：42- 46.

[17] TAKEZAWA A,NISHIWAKI S,KITAMURA M.Shape and topology optimization based on the phase field method and sensitivity analysis [J].Journal of Computational Physics,2010,229(7)：2697- 2718.

[18] TAKEZAWA A,YOON G H,JEONG S H,et al.Structural topology optimization with strength and heat conduction constraints [J].Computer Methods in Applied Mechanics and Engineering,2014,276：341- 361.

[19] KOGA A A,LOPES E C C,NOVA H F V,et al.Deve-lopment of heat sink device by using topology optimization [J].International Journal of Heat and Mass Transfer,2013,64：759-772.

[20] GUO X,ZHANG W,ZHONG W.Stress-related topology optimization of continuum structures involving multi-phase materials [J].Computer Methods in Applied Mechanics and Engineering,2014,268：632- 655.

[21] WANG Y,LUO Z,KANG Z,et al.A multi-material level set-based topology and shape optimization method [J].Computer Methods in Applied Mechanics and Engineering,2015,283：1570- 1586.

[22] TAVAKOLI R.Multimaterial topology optimization by volume constrained Allen-Cahn system and regularized projected steepest descent method [J].Computer Methods in Applied Mechanics and Engineering,2014,276：534- 565.

[23] 左孔天,钱勤,赵雨东,等.热固耦合结构的拓扑优化设计研究 [J].固体力学学报,2006,26(4)：447- 452. ZUO Kong-Tian,QIAN Qin,ZHAO Yu-dong,et al.Research on the topology optimization about thermo-structural coupling field [J].Acta Mechanica Solida Sinica,2005,26(4)：447- 452.

[24] 庄春刚.基于水平集的多材料结构拓扑优化设计方法与应用 [D].上海：上海交通大学,2007.

[25] 罗震.基于变密度法的连续体结构拓扑优化设计技术研究 [D].武汉：华中科技大学,2005.

[26] SIGMUND O.A 99 line topology optimization code written in Matlab [J].Structural and Multidisciplinary Optimization,2001,21(2)：120- 127.

Design of Thermal-Mechanical Coupling Multiple-Material Compliant Mechanisms Based on Parallel Strategy

ZHANGXian-minHUKaiWANGNian-fengGUOHao

(School of Mechanical and Automotive Engineering∥Guangdong Provincial Key Laboratory of Precision Equipment and Manufacturing Technology,Guangzhou 510640, Guangdong, China)

In the field of structural design, thermal effects have been extensively discussed. In this paper, based on the topology optimization method, the design of the thermally-driven compliant mechanism is investigated, and a corresponding parallel penalization model is constructed. The core of this model is to decompose a complex multiple-material thermal-mechanical coupling problem into a series of single-material thermal-mechanical coupling sub-problems. Then, the sub-problems are solved concurrently, and according to the requirement of the overall system, the solutions to all the sub-problems are coordinated so as to achieve the solution to the original problem. For all the sub-problems, the thermal-mechanical coupling optimization models are constructed based on the solid isotropic material with penalization(SIMP) model, and then the sequential coupling method is adopted to conduct the thermal-structural coupling physics analysis, thus achieving concurrent and independent solutions. The constructed model is simple in concept and practice and can be used to handle an arbitrary number of candidate materials. In addition, it can avoid fragile topologies and is, therefore, helpful in manufacturing. Finally, the effectiveness of the constructed model is verified by several numerical examples.

topology optimization; compliant mechanism; thermal-mechanical coupling; sensitivity analysis

2015- 12- 07

国家自然科学基金资助项目(51205134,51575187,91223201)；广州市产学研协同创新重大专项(2014Y2-00217)；广东省自然科学基金资助项目(S2013030013355)；黄埔区重大专项(20150000661)；华南理工大学中央高校基本科研业务费专项资金资助项目(2015ZZ007) Foundation items: Supported by the National Natural Science Foundation of China(51205134,51575187,91223201) and the Natural Science Foundation of Guangdong Province(S2013030013355)

张宪民(1964-)，男，教授，博士生导师，主要从事机构学及精密制造装备研究.E-mail：zhangxm@scut.edu.cn

† 通信作者: 王念峰(1978-)，男，教授，博士生导师，主要从事结构优化及机器人技术研究.E-mail：menfwang@scut.edu.cn

1000- 565X(2016)10- 0022- 07

TB 112；TB 114

10.3969/j.issn.1000-565X.2016.10.004