基于时域显式法的非平稳随机地震响应灵敏度分析*

李雪平 李栋泓 苏成 魏鹏

(华南理工大学 土木与交通学院∥亚热带建筑科学国家重点实验室， 广东 广州 510640)

基于时域显式法的非平稳随机地震响应灵敏度分析*

李雪平 李栋泓 苏成 魏鹏†

(华南理工大学 土木与交通学院∥亚热带建筑科学国家重点实验室， 广东 广州 510640)

分别采用精细积分格式和Newmark-β积分格式推导了非平稳随机地震响应灵敏度的时域显式表达式.并分别将其应用于平面框架与平面桁架问题的灵敏度分析,研究了积分时间步长对两种积分格式的计算精度和效率的影响.发现:当结构主频处于地震主频范围内时,在同等精度条件下,基于精细积分的时域表达式效率更高;而在结构主频偏离地震荷载主频范围时,基于Newmark-β积分格式的时域表达式效率更高.该研究成果可以为在考虑非平稳随机振动的结构优化问题中的数值积分算法选择提供有效的参考和借鉴.

灵敏度分析；时域显式法;非平稳随机动力响应

灵敏度分析即求导信息,在结构优化、最优控制和系统辨别等领域都有广泛的应用.它是评价结构参数的改变引起结构响应特性变化率的方法.在随机响应灵敏度分析中,国内外已有相关学者对此进行了研究.文献[1]对结构受随机激励的响应灵敏度进行分析,建立了有色噪声下响应协方差并推导了相应灵敏度表达式.文献[2]采用虚拟激励法推导平稳激励下的响应及灵敏度,并应用于求解带有不确定参数结构在平稳激励下的响应.文献[3]采用虚拟激励法,多次利用状态空间解耦及矩阵微分理论等,推导出多源随机激励下响应均方根的参数灵敏度表达式,并应用于汽车平顺性分析.文献[4]基于虚拟激励法,分别采用Newmark-β法推导了响应功率谱的一阶和二阶灵敏度的计算列式.文献[5]对于随机激励下随机结构动力响应的灵敏度问题进行分析,采用基于点估计法求解结构响应均方值的均值对结构参数的敏度信息.文献[6]在虚拟激励法的框架下,采用泰勒展开表达式求解随机结构受平稳激励的响应,并进行灵敏度分析.

近年来,由苏成等[7- 8]提出的时域显式法可显式表达出结构的动力响应表达式,并可高效求解结构在非平稳激励下的动力响应及动力可靠度.陈太聪等[9]基于精细积分格式提出了非平稳随机响应灵敏度的时域显式法.无论是动力响应还是灵敏度分析,其显式解均可表示为与结构参数有关的系数矩阵和与荷载有关的荷载向量乘积的表达式,而其中与结构参数有关的系数矩阵可采用精细积分法[10]、Newmark-β法[11]等积分方法来推导求得.而这些数值积分方法的计算效率和精度均与积分时间步长有关,但目前并未有文献对此进行细致分析.结构动力灵敏度分析是结构动力拓扑优化过程中所需要求解的重要信息.由于结构优化是一个动态逐步迭代的过程，每一步都需要求解目标函数和约束函数对设计参数的灵敏度,这样灵敏度的计算效率变得非常重要.因此,有必要对不同积分格式下的时域显式灵敏度分析方法进行研究，以便找到更高效的算法.文中首先基于时域显式法的思想，推导了两种积分格式下的非平稳随机响应灵敏度的时域显式理论公式,接着应用上述方法分别对一个平面框架和一个平面桁架在非平稳随机地震激励下的灵敏度进行了分析，并对计算精度和效率进行对比.

1 随机地震响应灵敏度分析的时域显式表达

1.1 基于精细积分法的时域显式表达式

考虑某n个自由度的线性结构系统,在随机地震作用下的动力学方程可以写为

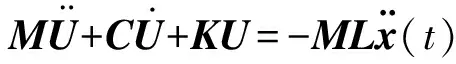
(1)

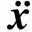
(1)

式中,

(3)

I为单位矩阵,当系统的初始状态V0=0时,由文献[7]可推导出第i时刻的响应Vi的时域显式表达式为

(4)

(i=1,2…,l)

式中,

(5)

其中,

(6)

式(4)中Ai只与结构参数有关,反映结构参数对动力响应的影响.则响应Vi可进一步表达为

(7)

式中,

(8)

(9)

(10)

式中,

(11)

1.2 基于Newmark-β法的时域显式表达式

采用Newmark-β数值积分格式推导出动力学方程(1)在第i时刻的响应Vi的显式递推关系式[12- 13]:

(12)

(i=1,2,…,l)

式中,

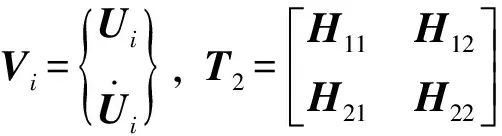
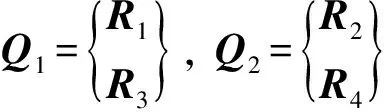
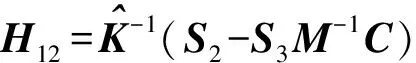
H21=a4(H11-I)+a6M-1K,

H22=a4H12-a5I+a6M-1C,

R3=a4R1-a6M-1,R4=a4R2,

S1=a1M+a4C,

S2=a2M+a5C,

S3=a3M+a6C,

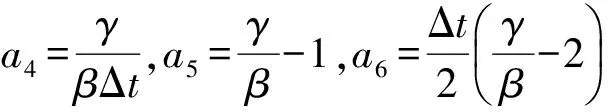
积分参数γ和β可分别取0.5和0.25,以保证数值积分的稳定性.注意此时递推矩阵T2与式(6)中T1不同.当系统的初始状态V0为零向量,并且记N=T2Q2+Q1时,由递推关系式可以推导出响应Vi的时域显式表达式:

(13)

式中,

(14)

其中,Ai也是只与结构参数有关,响应Vi也可进一步表达为与式(7)相同的形式,但其中的系数Bi表示如下:

(15)

由于在结构振动分析中一般只对结构某些关键部位响应感兴趣,通常并不需要求解所有的响应向量,从而可以节省大量的计算工作量.由式(7)可知,在时刻i某一关键部位的响应vi及方差可写为

(16)

(17)

其中,φ为关注结构响应的定位行向量,其元素由0和1组成.

同样,基于此思路也可推导动力响应灵敏度的时域显式求解列式.设θ代表结构的某设计参数,则对动力学方程式(1)两端求偏导,并考虑荷载与结构参数无关,则可得:

(18)

式中,

(19)

对比式(1)和式(19)可见,两方程仅荷载项不同，因此也可以采用Newmark-β法推导其灵敏度的时域表达式,形式与式(10)相同,其中的系数表示如下:

(20)

由式(7)和(10)可以看出,无论是响应还是灵敏度都可通过与结构参数相关的系数矩阵和与荷载相关的系数矩阵求得.而与结构相关的系数矩阵可通过精细积分法或Newmark-β法求得.根据随机响应的方差灵敏度的一般计算公式[14]:

(21)

将式(10)和(17)代入,整理可得第i时刻结构响应vi的方差对设计参数θ的灵敏度的计算表达式为

(22)

式中,

(23)

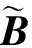
2 数值算例

以下将通过平面框架结构和桁架结构的算例对比两种积分格式在不同时间步长下所求得的响应及灵敏度,并分析时间步长对两种积分格式精度和效率的影响.

2.1 平面框架结构

(24)

其中,t1=3s,t2=6s,t3=15s,c=0.157 2.f(t)为一零均值高斯平稳随机过程,其功率谱密度函数取为Kanai-Tajimi过滤白噪声谱,即

(25)

式中ωg=14rad/s(地基土的卓越频率),ζg=0.6(地基土的阻尼比),S0=0.07N2/Hz(谱强度因子),其功率谱密度图如图2所示.设计参数分别取为柱边长、梁高、材料的弹性模量.计算步长分别取Δt=0.005,0.010,0.020,0.050s,则A点的位移方差灵敏度时程曲线如图3所示.

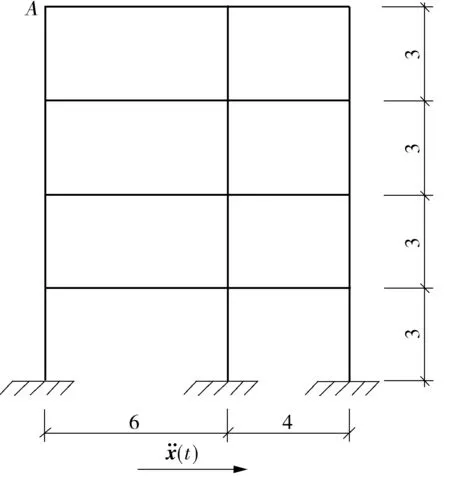
图1 平面框架结构模型(单位：m)

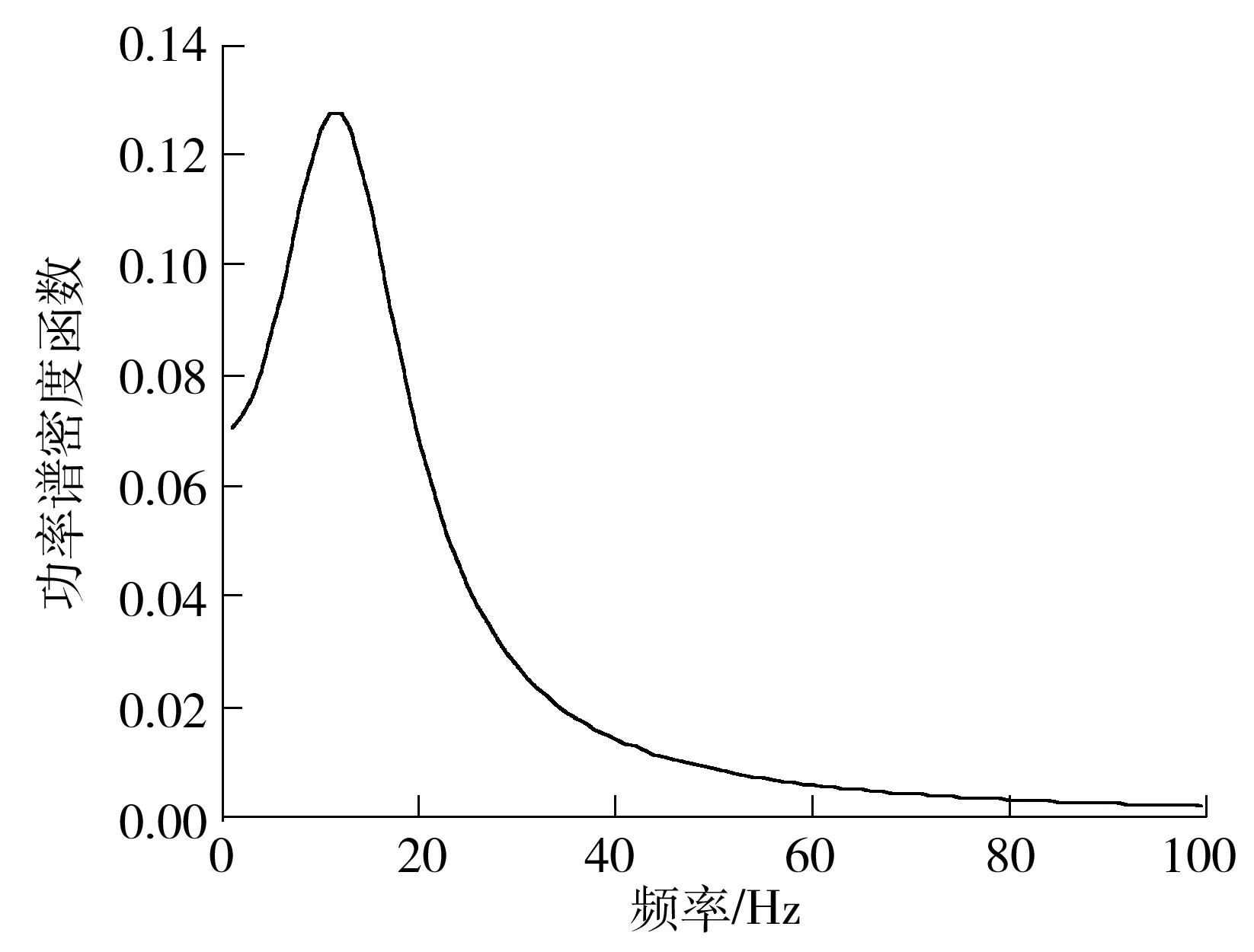
图2 功率谱密度函数

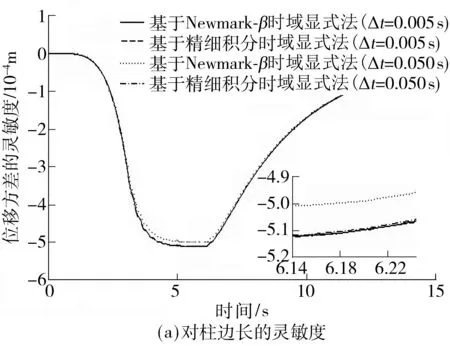
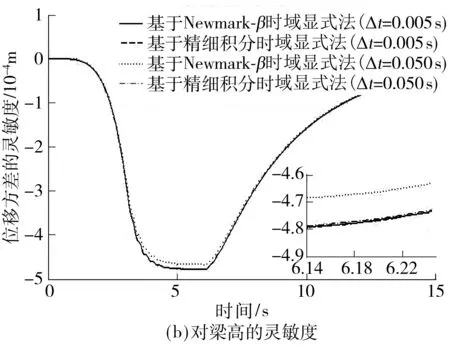
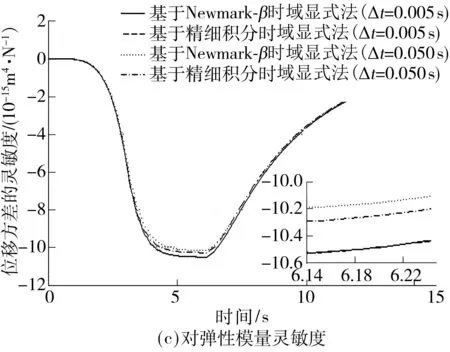
图3 A点的位移方差的灵敏度时程曲线

Fig.3 Sensitivity time history of the displacement variance of nodeA

表1给出了A点位移方差对弹性模量的灵敏度时程.从表1中可以看出,当积分步长为0.005 s时,基于两种积分格式的时域显示法求得的位移方差及灵敏度一致,以此作为精确解.随着积分步长的变大两种积分格式的精度受到不同程度的影响.若以最大相对误差在5%以内为界限,则Newmark-β法允许的最大积分步长为0.020 s,而精细积分法允许的最大积分步长为0.050 s,两种方法所用时间比为1.4∶0.2(即7倍).此时在相同精度下基于精细积分法的时域显式法计算效率更高,而此时结构的主频正处于荷载的主频范围内.

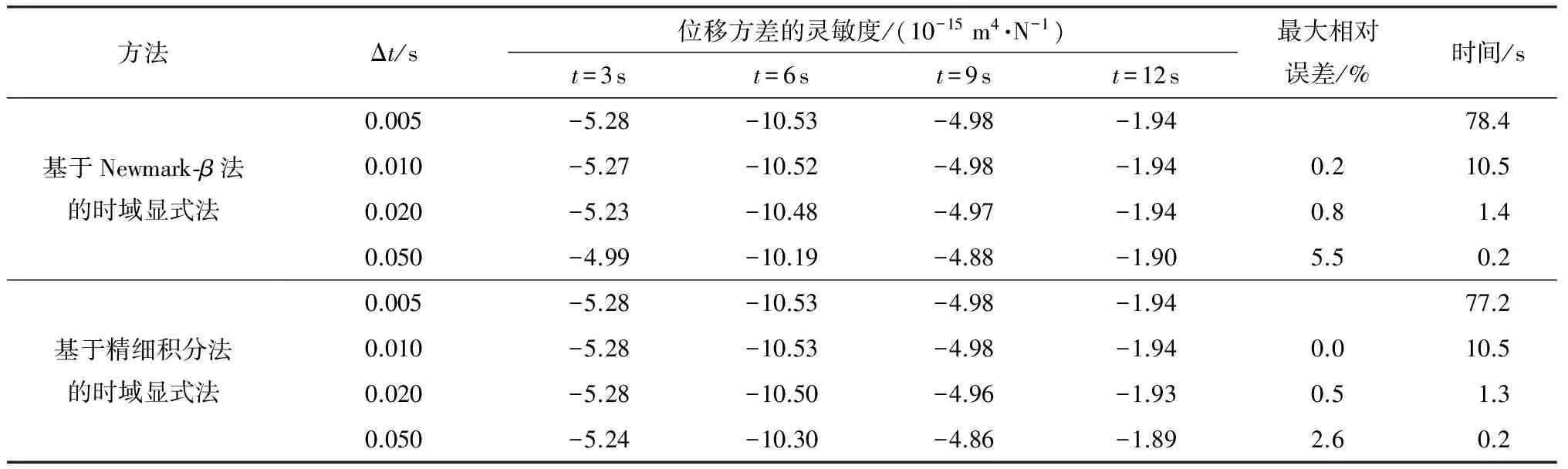
表1 A点位移方差对弹性模量的灵敏度时程

2.2 平面桁架结构

某输电塔结构如图4所示,该结构有限元模型采用24个平面杆单元,共20个自由度,材料弹性模量E=2.1×1011N/m2,质量密度ρ=7 800 kg/m3,考虑输电线的自重,节点9和节点12具有集中质量m=1 200 kg,其余节点具有集中质量m=600 kg.阻尼采用Rayleigh阻尼,其中的阻尼系数α1=0.2,α2=0.005,结构前三阶频率分别为35.7、128.3、136.6 rad/s.考虑非平稳地震作用与算例2.1节相同.设计参数分别取为节点8的x坐标和21号杆截面面积A1.计算步长分别取Δt=0.002,0.005,0.010,0.020 s,则节点12的水平位移方差灵敏度时程曲线如图5所示.

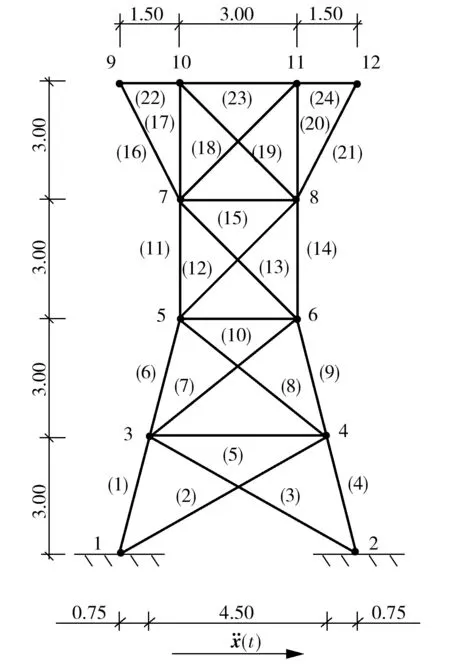
图4 平面桁架结构模型(单位：m)

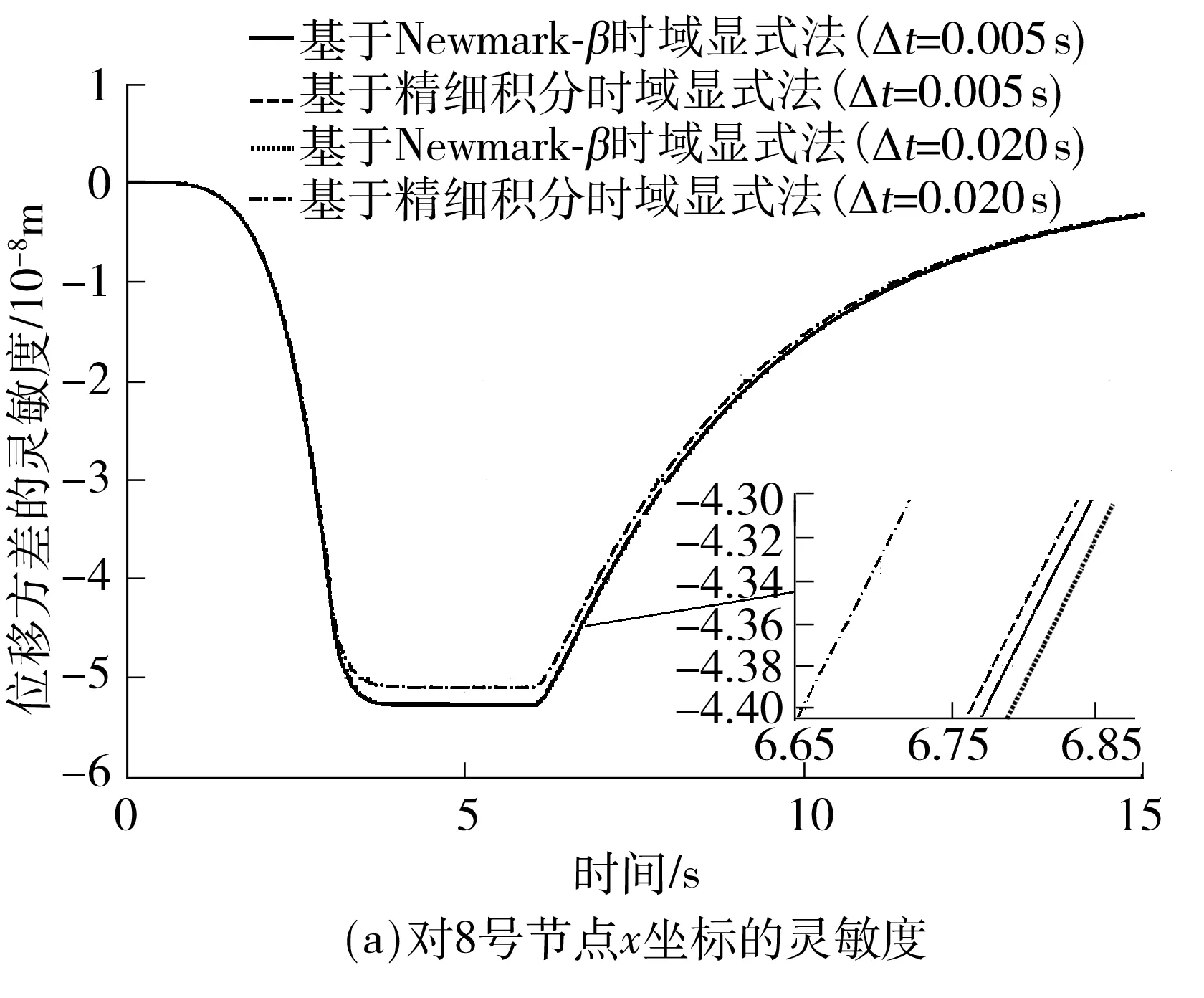
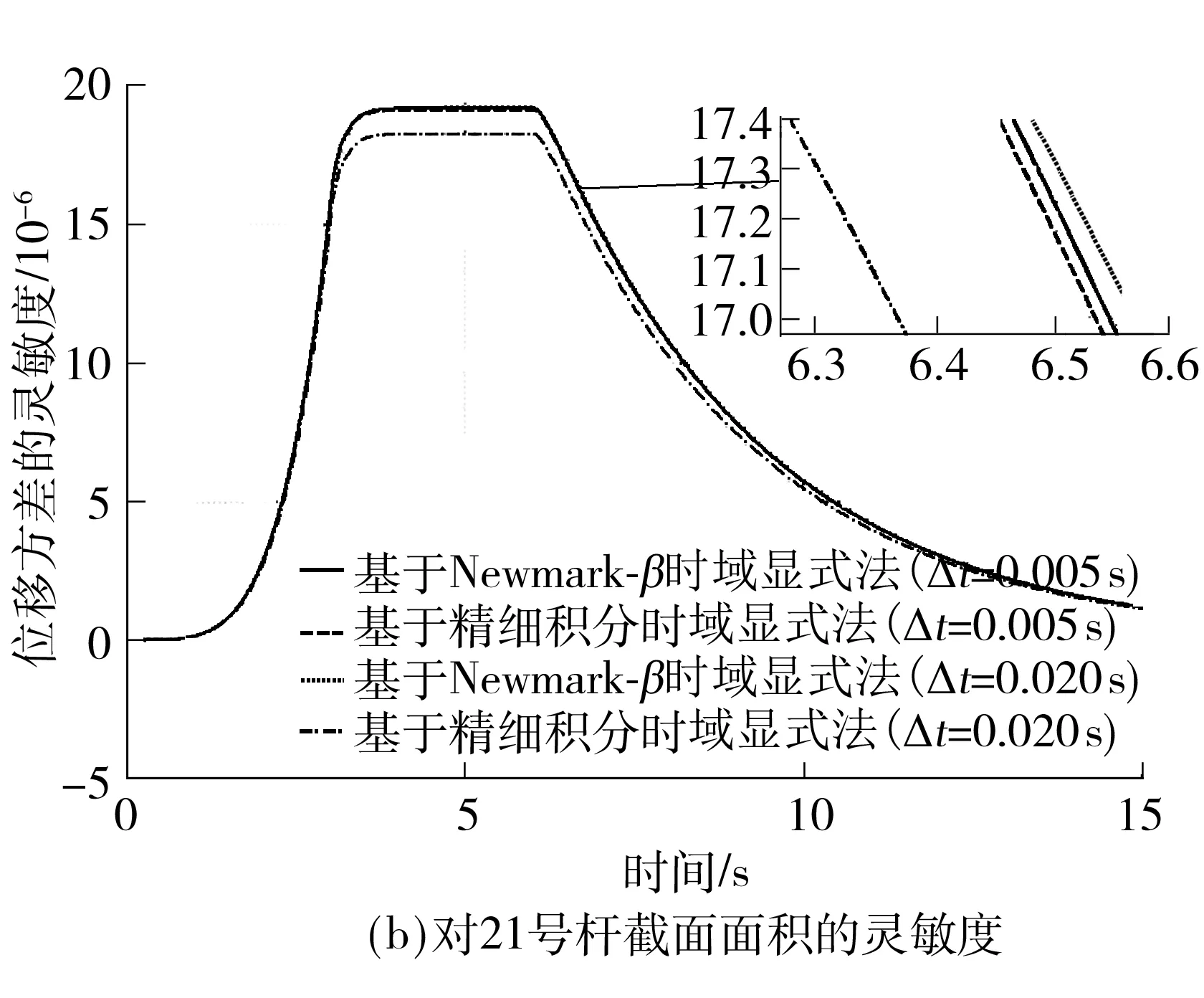
图5 节点12的位移方差灵敏度时程曲线(单位：m)

Fig.5 Sensitivity time history of the displacement variance of node 12(Unit:m)

由以上推导已求得结构的位移和速度的方差及相应的灵敏度,若关注的是桁架结构在随机地震下的应力方差及相应的灵敏度则可进一步推导第j根杆的第i时刻的应力为

(26)

式中,

(27)

相应的第j根杆的第i时刻的应力灵敏度为

(28)

则第j根杆的第i时刻的应力方差为

(29)

相应的第j根杆的第i时刻的应力方差灵敏度为

(30)

式中,

(31)

以下选取21号杆进行应力方差灵敏度的求解,设计参数同上,结果如图6所示.

同样,当积分步长为0.002 s时,两种积分格式求得的位移方差及灵敏度一致,以此作为精确解.表2列出了21号杆截面面积在某些时刻点处对其

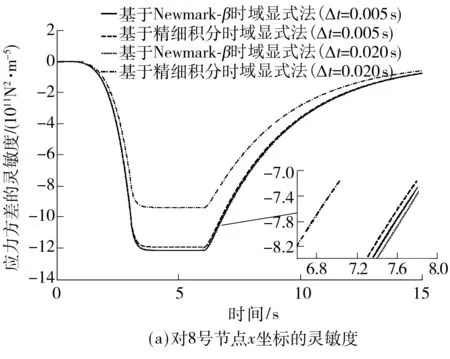
图6 21号杆件应力方差的灵敏度时程曲线

应力方差的灵敏度值,若以最大相对误差在5%以内为界限,则Newmark-β法允许最大的积分步长为0.02 s,精细积分允许最大的积分步长为0.01 s.两种方法所需时间比为33.8∶5.1(即6.62倍).即在相同的精度下,基于Newmark-β法的时域显示法计算效率更高,而此时的结构主频偏离荷载主频范围.

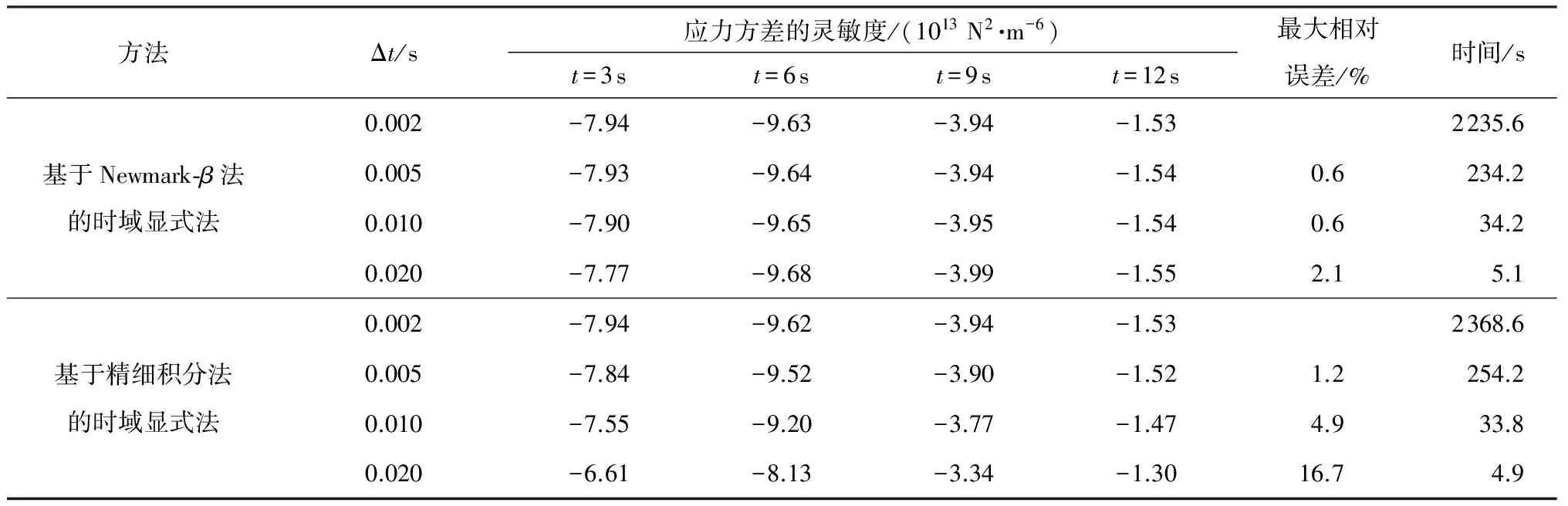
表2 21号杆的应力方差对其截面面积的灵敏度时程

3 结论

文中用两种不同的数值算法推导了结构动力响应灵敏度的两种时域显式格式,通过两个数值算例的对比发现:在求解非平稳随机地震响应的灵敏度过程中,当结构的主频位于地震荷载主频范围内时,在同等精度条件下,基于精细积分法的时域显式的灵敏度计算效率更高;而在结构的主频偏离地震荷载主频范围时,基于Newmark-β法的灵敏度计算效率更高.因此,为了提高结构动力响应优化的计算效率,在保证精度的前提下,对不同结构选用具体的数值计算方法时必须考虑结构的主频与地震荷载频率的分布特性.文中结论可以广泛应用于结构在随机荷载下的动力灵敏度分析，为数值积分算法的选择提供依据.

[1] 姚昌仁,麻永平.结构随机激励的响应灵敏度分析 [J].力学学报,1990,22(1):438- 445. YAO Chang-ren，MA Yong-ping.The response sensitivity analysis for structural systems in random excitation [J].Chinese Journal of Theoretical and Applied Mechanics，1990,22(1):438- 445.

[2] 王凤阳.基于虚拟激励的随机振动灵敏度分析及其应用 [D].大连:大连理工大学,2010.

[3] 唐帆,王锡平,朱文海,等.多源随机激励系统的参数灵敏度分析 [J].振动与冲击,2012,31(1):82- 85. TANG Fan，WANG Xi-ping，ZHU Wen-hai，et al.Parameter sensitivity analysis for a system with multi-source random excitation [J].Journal of Vibration and Shock，2012,31(1):82- 85.

[4] LIU Q.Sensitivity and Hessian matrix analysis of power spectral density functions for uniformly modulate devolutionary random seismic responses [J].Finite Elements in Analysis and Design，2012,48:1370- 1375.

[5] 乔红威,吕震宙.随机结构随机激励下的响应灵敏度分析 [J].振动与冲击,2008(3):60- 62,179. QIAO Hong-wei，LÜ Zhen-zhou.Response sensitivity analysis of stochastic structures under random excitation [J].Journal of Vibration and Shock，2008(3):60- 62,179.[6] ZHAO Y，WANG F.Sensitivity analysis for structures subjected to stationary random excitations [J].Procedia Engineering，2011,14:2475- 2480.

[7] 苏成,徐瑞.非平稳激励下结构随机振动时域分析法[J].工程力学,2010,27(12):77- 83. SU Cheng，XU Rui.Random vibration analysis of structures subjected to non-stationary excitations by time domain method [J].Engineering Mechanics，2010,27(12):77- 83.

[8] 苏成,徐瑞.非平稳随机激励下结构体系动力可靠度时域解法 [J].力学学报，2010,42(3):512- 520. SU Cheng,XU Rui.Time-domain method for dynamicreliability of structural systems subjected to non-stationary random excitations [J].Chinese Journal of Theoretical and Applied Mechanics，2010,42(3):512- 520.

[9] 陈太聪,苏成,胡智强,等.非平稳随机响应灵敏度分析的时域显式法 [J].振动工程学报,2015,28(4):43- 49. CHEN Tai-cong，SU Cheng，HU Zhi-qiang，et al.An explicit time-domain method in sensitivity analysis of non-stationary stochastic responses [J].Journal of Vibration Engineering，2015,28(4):43- 49.

[10] 钟万勰.结构动力方程的精细时程积分法 [J].大连理工大学学报,1994,34(2):131- 136. ZHONG Wan-xie.On precise time-integration method for structural dynamics [J].Journal of Dalian University of Technology，1994,34(2):131- 136.

[11] NEWMARK N M.A method of computation for structural dynamics [J].Journal of Engineering Mechanics Division，1959,85(3):67- 94.

[12] 余超.基于时域显式法的结构瞬时最优控制 [D].广州:华南理工大学，2015.

[13] SU Cheng，HUANG Huan，MA Hai-tao，et al.Random vibration analysis of hysteretic systems by explicit iteration Monte-Carlo simulation method [J].Earthquakes and Structures，2014,7(2):119- 139.

[14] CACCIOLA P，COLAJANNI P，MUSCOLINO G.A modal approach for the evaluation of the response sensitivity of structural systems subjected to non-stationary random Processes [J].Computer Methods in Applied Mechanics and Engineering，2005,194:4344- 4361.

Sensitivity Analysis of Non-Stationary Random Seismic Response Based on Time-Domain Explicit Method

LIXue-pingLIDong-hongSUChengWEIPeng

(School of Civil Engineering and Transportation∥State Key Laboratory of Subtropical Building Science，South China University of Technology，Guangzhou 510640，Guangdong，China)

In this paper，two time-domain explicit expressions of the non-stationary random seismic response sensitivity are derived respectively based on the precise integration format and the Newmark-βintegral format，and they are respectively used to analyze the sensitivity of a plane frame and a plane truss structure.Then，the effects of the integral time step on the calculation accuracy and the efficiency of the two integral formats are investigated.It is found that，when the main frequency of the structure is within the range of the main load frequency，the time-domain explicit expression based on the precise integration has a higher efficiency with the same accuracy，but when the main frequency of the structure deviates from the main load frequency range，the time-domain explicit expression based on the Newmark-βintegral format achieves a higher efficiency.The research achievements can provide an effective reference for the choice of the numerical integration algorithms used in the structure optimization consi-dering the non-stationary random vibration.

sensitivity analysis；time-domain explicit method；non-stationary random seismic response

2015- 10- 19

国家自然科学基金资助项目(11372004);华南理工大学中央高校基本科研业务费专项资金资助项目(2014ZZ0071) Foundation items: Supported by the National Natural Science Foundation of China(11002056,11372004)

李雪平(1978-),男,博士,副研究员,主要从事结构振动、控制、优化与系统可靠度分析研究.E-mail:xueping@scut.edu.cn

† 通信作者: 魏鹏(1978-),男,博士,副教授,主要从事结构优化方法研究.E-mail:ctpwei@scut.edu.cn

1000- 565X(2016)10- 0110- 07

O 324;TU311

10.3969/j.issn.1000-565X.2016.10.016