考虑重力影响的单层网壳冲击相似律及数值验证*

姜正荣 钟渝楷 石开荣† 罗斌

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640； 3.东南大学 土木工程学院， 江苏 南京 211189)

考虑重力影响的单层网壳冲击相似律及数值验证*

姜正荣1,2钟渝楷1石开荣1,2†罗斌3

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640； 3.东南大学 土木工程学院， 江苏 南京 211189)

考虑重力作用和材料的应变率效应，根据量纲分析，推导出单层网壳在顶点受冲击物冲击的相似律表达式，并在此基础上，提出可通过特别制备材料或添加配重的方法来满足相似条件.采用非线性有限元软件LS-DYNA建立与已有文献一致的模型，对比试验结果，验证数值方法的可靠性；建立凯威特-联方型单层网壳分析模型，以节点位移为考察量，分别对提出的两种方法进行验证.结果表明：文中提出的两种方法均能较好地预测原型的位移，相对误差绝对值分别小于15%和12%；均能准确预测网壳的倒塌模式，特别是工程关注的整体倒塌；添加配重的方法具有更高的精度和可操作性.

相似律；应变率效应；重力；单层网壳

由于造型优美、轻巧且刚度大，网壳结构被广泛应用于体育场馆等人员密集的建筑.但近年来，恐怖袭击和意外爆炸冲击时有发生，此类建筑一旦遭受破坏，必将造成严重的社会影响.因此，对网壳结构的抗冲击性能研究很有必要.

目前，国内外对单层网壳冲击动态响应的研究已较为全面，并取得了一系列成果[1- 5].然而上述研究均未涉及相似律，鉴于此，有必要建立试验模型与原型之间的相似关系.

由于材料的应变率效应、重力、材料断裂等因素的影响，结构在冲击荷载下往往难以满足传统的相似关系[6].Oshiro等[7- 8]对应变率引起的相似畸变进行了深入的研究，并通过修正模型速度以考虑应变率的影响；秦健等[9]采用该方法较好地预测了船舶原型在爆炸荷载下的动态响应.除了应变率效应，单层网壳受冲击时还需考虑重力影响[4]，目前对重力影响的研究主要集中于模型在振动台上的动力试验[10]，且极少有综合考虑应变率效应和重力影响的相似律研究.

为此，文中考虑应变率效应和重力作用，对单层网壳在冲击荷载下的相似律进行推导，得到模型预测原型所需满足的相似关系，并根据试验条件，提出两种满足相似律的实用方法.采用LS-DYNA建立凯威特-联方型单层网壳算例，对理论推导结果进行数值模拟分析验证.

1 考虑重力作用的相似律

与冲击荷载相比，重力相对较小，一般可以忽略，故绝大部分冲击相似律研究不考虑重力影响.但网壳在冲击下有倒塌的可能性，临界倒塌时，考虑重力与否的计算结果往往差别很大，故重力作用不能忽略[4].

假设模型和原型冲击姿态和边界条件相同，同时忽略碰撞过程中的热效应，考虑冲击作用为双重非线性问题，忽略弹性模量的变化，则网壳顶点受冲击物冲击时的位移可表示为

w=f(aq,aq1,…,aqn,ρq,νq,Yq;

(1)

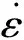
以l、ρ和Y为基本物理量，式(1)可化为无量纲函数关系：

(2)

考虑原型与模型几何相似、冲击物与网壳采用相同材料，式(2)可简化为

(3)

与模型相关的物理量用下标m表示，与原型相关的物理量用下标p表示，βX=Xm/Xp表示模型和原型相关物理量的比值.若原型和模型满足相似关系，需满足(Πi)m=(Πi)p,i=1,2,3.

由(Π1)m=(Π1)p得

(4)

由于模型与原型重力场一致，即βg=1，由(Π2)m=(Π2)p得

βY=βlβρ

(5)

由式(5)得密度比

βρ=βY/βl

(6)

将式(5)代入式(4)，得速度比

(7)

由式(5)和(Π3)m=(Π3)p得应变率比

(8)

材料在冲击荷载作用下，考虑应变率可用Cowper-Symonds模型表示[6]：

(9)

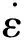
由式(9)有

(10)

将式(10)代入式(6)得

(11)

其中，由于原型采用钢材，故Ysp=235MPa.

由式(11)可知，由于应变率的变化，要满足相似关系，不同几何比下，需变化质量密度或动态屈服强度，这与余同希等[12]得出的结论是一致的.对此，有两种处理方式.

方法一 根据相似关系直接选择模型材料，不同几何比和冲击速度下选择的材料不同，且材料可能需特别制造.

模型与原型满足相似关系，由式(7)、(8)和(11)可得网壳材料参数(见表1).

表1 材料参数1)

1)1/10和1/20表示模型与原型的几何比.

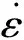
方法二 模型采用现有的材料，通过添加配重变相满足质量密度比的要求.

以模型与原型材料相同(模型也采用钢材)为例，式(10)化简为

(12)

由式(6)得质量密度比

(13)

表2给出了不同速度和几何比下动态屈服强度比βY和质量密度比βρ.

表2 不同速度和几何比下βY和βρ的值1)

Table2ValuesofβYandβρunderdifferentvelocitiesandgeometricscalings

速度/(m·s-1)βYβρ1/101/201/101/2051．06941．098510．694121．9691101．07671．108510．766722．1709201．08441．119210．843622．3835301．08901．125610．890322．5125401．09241．130310．924222．6058

1)1/10和1/20表示模型与原型的几何比.

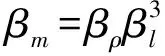
(14)

式中，ma为模型需添加的质量，mp为原型的质量，mm为模型的质量.

根据方法二，利用已有的材料(如钢材)，通过配重来变相满足质量密度比的要求，从而满足相似关系.此方法无需特殊制备材料，不同几何比通过不同配重均可满足相似关系，较为简单方便.框架振动台模型试验主要通过铁板等重物添加配重[10]，网壳试验模型的荷载和配重往往等效为节点质量，通过配重块固定在节点上[13]或直接增大节点[14].

2 相似律的数值验证

基于上述推导过程，对具有实际工程意义的凯威特-联方型单层网壳顶点受冲击物冲击进行数值模拟，并验证相似律结果的准确性.

2.1 有限元模型验证及分析模型的建立

采用吴长[15]的试验模型进行数值模拟对比，以验证数值方法的可靠性.试验模型为一跨度 3 m、 矢高 0.667 7 m 的 K6 型单层球面网壳结构.主肋及环杆圆钢管为φ22 mm×3 mm，斜杆圆钢管为φ14 mm×2 mm，采用球节点模拟集中质量，附加质量约为2.0 kg/节点，节点规格为D80.利用钢球进行冲击试验，在5 200 mm高冲击模拟试验台释放，坡度为42°.如图1 所示，C代表冲击点,W代表位移测点，数字代表应力测点.

图1 网壳测点和冲击点示意图

Fig.1 Schematic diagram of measuring points and impact points of reticulated shell

采用LS-DYNA软件建立有限元模型.杆件采用BEAM161单元，每根杆件划分为3个单元，本构关系采用分段线性塑性模型，质量密度ρ=7 850 kg/m3，泊松比ν=0.3，弹性模量E=206 GPa，屈服强度为235 MPa，失效应变为0.25，强化系数a=40 s-1，b=5.钢球采用SOLID165单元，本构关系采用刚体，材料基本参数与杆件一致.节点采用质量单元MASS166，整个模型施加重力场，钢球与网壳接触采用点面接触(NODE-TO-SURFACE).

选取直径100 mm的钢球冲击C2点，获得杆件应力，并与试验结果对比，如表3所示；选取直径100 mm的钢球冲击C1点，得到节点水平位移，并与试验结果对比，如表4所示.

由表3和表4可见，模拟值和试验值吻合较好，除个别数据偏差较大外，其他值均较为接近，变化规律也一致.造成模拟值和试验值出现偏差的原因主要有：数值模拟不考虑试验过程中杆件和节点损伤累积和碰撞摩擦损失的能量；节点等效为质量点造成误差；试验过程中钢球难以对准节点冲击，且网壳瞬间振动大可能使电阻丝断开等.考虑到以上因素，数值模拟与试验结果吻合较好说明数值方法是可靠的.

表3 杆件轴向应力模拟值与试验值对比

Table 3 Comparison of axial stress between numerical simulation and experiment

杆件编号轴向应力/MPa模拟值试验值杆件编号轴向应力/MPa模拟值试验值156．7552．811105．71112．0255．5958．51229．9933．2394．2283．21336．4949．2490．0852．81446．8336．55104．9454．61559．0722．4638．7545．01657．1737．4781．2772．91744．4928．1829．4337．71823．0322．1945．3465．11929．9729．31085．8180．12039．5032．6

表4 节点水平位移模拟值与试验值对比

Table 4 Comparison of nodal horizontal displacement between numerical simulation and experiment

测点位置水平位移/mm模拟值试验值W10．6460．640W20．5830．640W30．3780．335W40．5780．356

在此基础上，建立跨度60 m、矢跨比1/6的凯威特-联方型单层球面网壳作为原型(见图2).凯威特型网格的主肋和环肋采用φ180 mm×8 mm，斜杆采用φ168 mm×6 mm；外围两环联方型环肋为φ168 mm×5.5 mm，斜杆为φ180 mm×7 mm，均为圆钢管.冲击物采用直径3 m、高度1 m的圆柱体，离网壳顶点1 m，冲击网壳顶点.材料参数与上述试验模型一致，但冲击物的本构关系采用分段线性塑性模型.

图2 凯威特-联方型单层网壳模型

根据原型建立几何比分别为1/10和1/20的模型，模型速度分别为5、10、20、30、40 m/s，进行算例验证.根据式(7)可得各模型速度对应的原型速度，列于表5中，可以看出，模型使用较小的冲击速度便可模拟原型较高速度的冲击.

表5 模型与原型对应速度1)

1)1/10和1/20表示模型与原型的几何比.

2.2 方法一分析与验证

采用前文方法一，即通过改变材料特性如质量密度、弹性模量等)来满足相似律，利用表1的材料参数进行数值模拟，结果分别见表6和表7.其中，表中模型速度对应的原型速度见表5.

表6 几何比1/10模型预测原型位移的结果(方法一)

Table 6 Displacement prediction of the prototype using model with geometric scaling 1/10(Method No.1)

模型速度/(m·s-1)模型位移/m预测位移/m原型位移/m相对误差/%51．079010．79011．830-8．79102．084720．84720．977-0．62200．25902．5902．924-11．42300．26272．6272．4696．40400．25392．5392．782-8．73

表7 几何比1/20模型预测原型位移的结果(方法一)

Table 7 Displacement prediction of the prototype using model with geometric scaling 1/20(Method No.1)

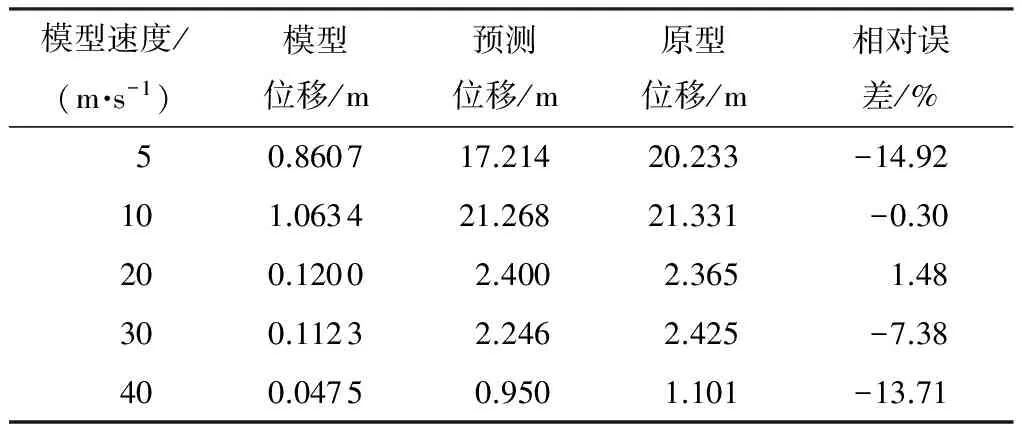
模型速度/(m·s-1)模型位移/m预测位移/m原型位移/m相对误差/%50．860717．21420．233-14．92101．063421．26821．331-0．30200．12002．4002．3651．48300．11232．2462．425-7．38400．04750．9501．101-13．71

由表6和表7可知，采用特别制备材料的模型能较好地预测原型的竖向位移，相对误差绝对值均小于15%，且位移变化规律一致.单层网壳受冲击时较为关心的是其倒塌模式，特别要避免结构出现整体倒塌.模型能够精确地预测原型的倒塌模式，如模型冲击速度为10 m/s时，几何比分别为1/10和1/20的模型和原型均整体倒塌，模型预测相对误差绝对值均小于1%.故方法一可较好地预测实际结构的倒塌模式，且位移误差较小.

由于模型选用的材料为假设材料，难以得知其具体的本构关系，需通过实际制备后测量，故与钢材的本构并不完全满足相似关系.实际试验时除非利用相同材料，否则很难使两种材料的本构满足相似关系，这是选材的难点.同时无法考虑材料断裂的相似关系，导致整体上模型预测原型的位移存在一定误差，且速度较小(如5 m/s)和速度较大(如40 m/s)时误差均较大.主要原因是量纲分析时忽略了弹性模量的变化，冲击速度较小时，网壳较大范围未进入塑性，且弹性区域受弹性模量影响较大；此外，由于等效应变率采用vq/l近似表示，与实际应变率有误差，故冲击速度越大，误差越大.

2.3 方法二分析与验证

若模型材料采用钢材，通过改变质量密度以满足相似律，质量密度比见表2，位移对比结果如图3所示.

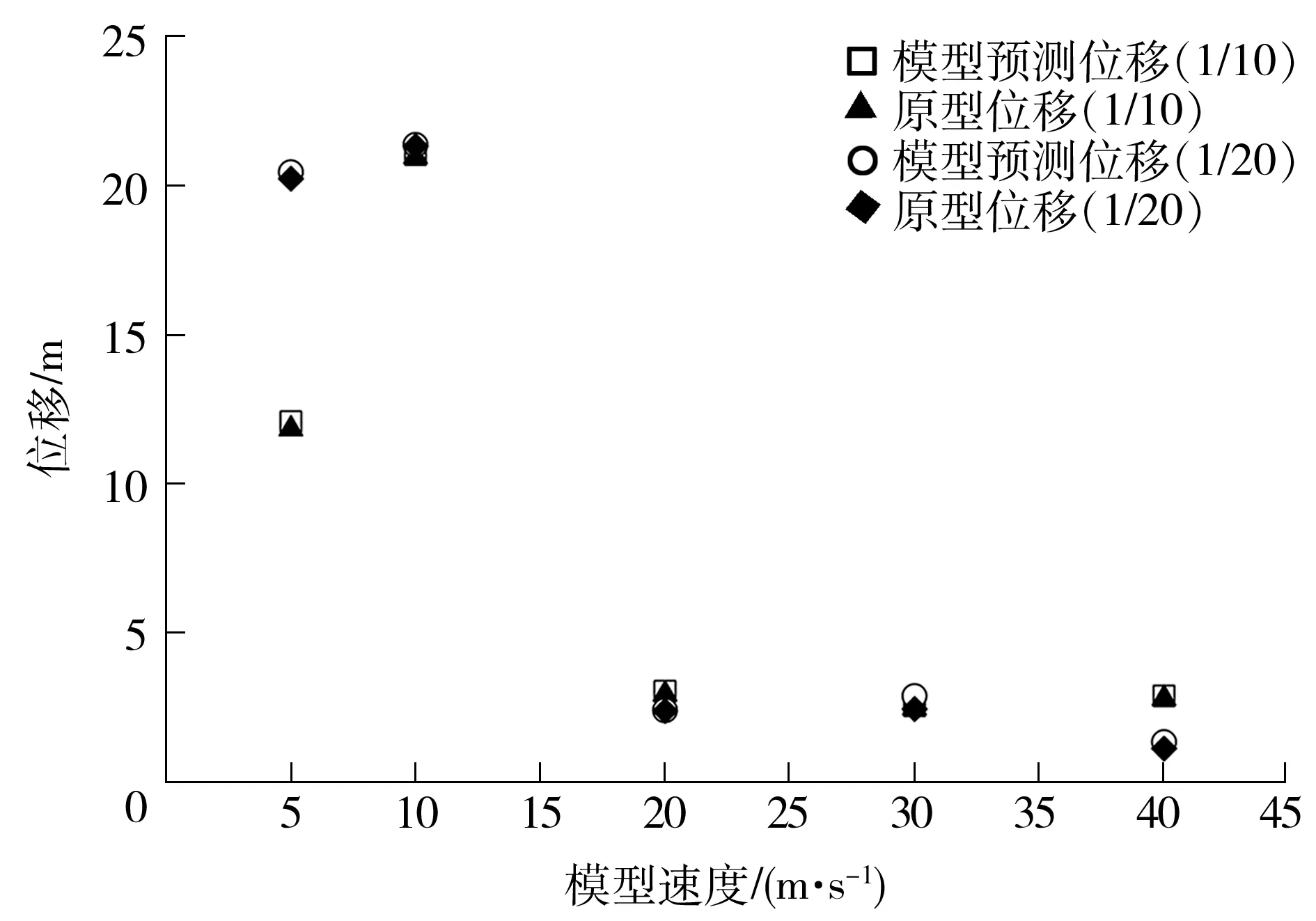
图3 模型预测位移与原型位移的对比

Fig.3 Comparison of displacement between model prediction and prototype

由图3不难看出，通过修改模型质量密度以满足相似律的方法能很好地预测原型位移，除个别数据外，相对误差均小于4%，说明了文中推导的相似律的准确性.

然而，实际试验时并不能随意改变材料的质量密度，有必要寻求可用于试验的近似方法.如前文所述，方法二通过添加配重来满足质量密度比.考虑到添加其他材料配重块较为麻烦，故网壳通过增大节点实现配重，冲击物通过增大圆柱体高度实现配重.此方法使冲击物在高度方向不满足几何相似关系，但通过使冲击高度满足几何相似进行了弥补.

对于网壳，原型质量mp=82 673.5 kg，1/10模型质量mm=82.670 8 kg，1/20模型质量mm=10.335 kg；对于冲击物，原型质量mqp=55 488.382 kg，1/10模型质量mqm=55.488 4 kg，1/20模型质量mqm=6.936 kg.由式(14)计算可得不同几何比的模型需添加的配重(表8、9)，其中，冲击物柱体高度为添加配重折算的高度与原高度之和，等效节点质量为配重平均到264个节点的质量.

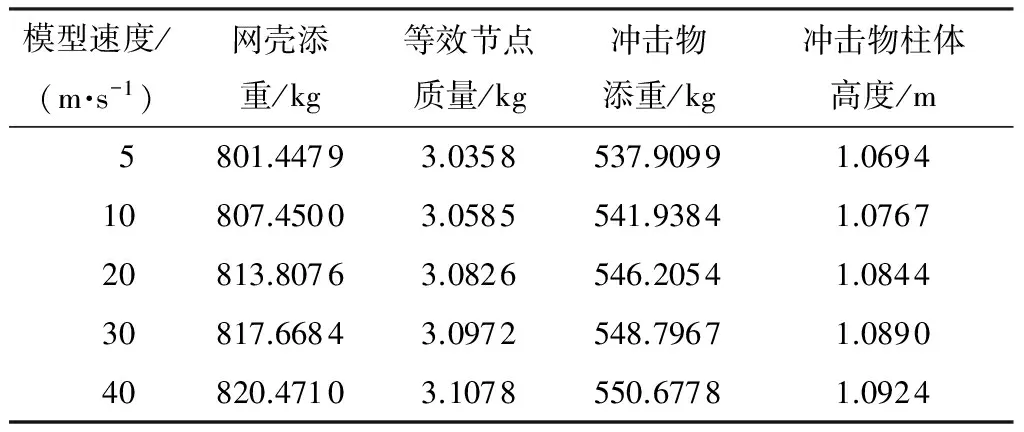
表8 几何比1/10模型添加配重Table 8 Adding extra mass to model with geometric scaling 1/10

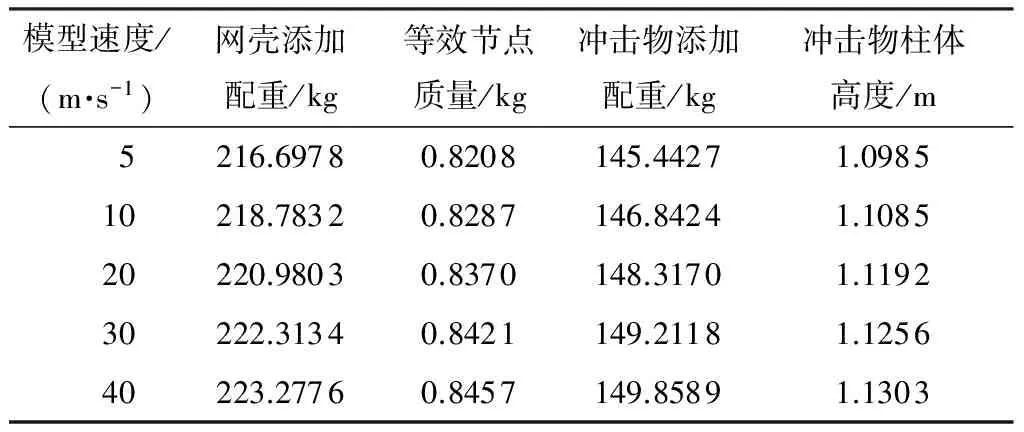
表9 几何比1/20模型添加配重Table 9 Adding extra mass to model with geometric scaling 1/20

对于几何比1/10模型，其最大节点直径约为0.045 m，而两个节点最小间距为0.312 m，此尺寸试验可以实现.同理，对于几何比1/20模型，其最大节点直径约为0.03 m，而两个节点最小间距为0.155 m，此尺寸试验同样可以实现.文献[14]进行了大节点网壳模型的振动台试验，跨度2.7 m的网壳配置直径250 mm的节点，结果表明，通过增大节点添加配重是可靠的.表10和表11为相应的计算结果.

由表10、11可见，不同几何比的模型均能很好地预测原型的竖向位移，除个别数据外，相对误差均小于12%，位移变化规律和网壳倒塌模式均与原型一致，由此说明，利用节点添加配重的方法是可行的.

表10 几何比1/10模型预测原型位移的结果(方法二)

Table 10 Displacement prediction of prototype using model with geometric scaling 1/10(Method No.2)

模型速度/(m·s-1)模型位移/m预测位移/m原型位移/m相对误差/%51．194511．94511．8300．97102．070920．70920．977-1．28200．27362．7362．924-6．43300．24792．4792．4690．41400．25842．5842．782-7．12

表11 几何比1/20模型预测原型位移的结果(方法二)

Table 11 Displacement prediction of prototype using model with geometric scaling 1/20(Method No.2)

模型速度/(m·s-1)模型位移/m预测位移/m原型位移/m相对误差/%51．018720．37420．2330．70101．057121．14221．331-0．89200．10672．1342．365-9．77300．11512．3022．425-5．07400．06121．2241．10111．17

由于配重等效为节点质量，导致实际质量分布比直接增大质量密度更不均匀，从而造成一定的预测误差.同样，由于应变率的近似取值，冲击速度越大，误差相应增大.相比方法一需特别制备材料，方法二通过添加配重以满足质量密度比的方法实现较为方便，且由于采用与原型相同的材料，避免了材料性质不同造成的误差.方法一和方法二的最大相对误差绝对值分别为14.92%和11.17%，说明方法二具有较高精度.综上所述，方法二具有更好的可操作性和精度，建议采用方法二进行模型试验.

3 结论

(1) 对网壳模型进行冲击试验时，可通过特别制备材料(方法一)或直接添加配重(方法二)来满足考虑重力作用和应变率效应的相似律.

(2) 文中两种方法均能精确地预测原型网壳的倒塌模式，且预测的竖向位移值具有较高精度，相对误差绝对值分别小于15%和12%.

(3)通过添加节点配重和增大冲击物圆柱体高度的配重法(方法二)具有较好的可操作性和更高精度，建议采用该方法进行类似结构的模型试验.

[1] 李海旺,郭可,魏剑伟,等.撞击载荷作用下单层球面网壳动力响应模型实验研究 [J].爆炸与冲击,2006,26(1):39- 45. LI Hai-wang,GUO Ke,WEI Jian-wei,et al.The dynamic response of a single layer reticulated shell to drop hammer impact [J].Explosion and Shock Waves,2006,26(1):39- 45.

[2] 郭可.单层球面网壳在冲击载荷作用下的动力响应分析 [D].太原:太原理工大学,2004.

[3] FAN F,WANG D Z,ZHI X D,et al.Failure modes of reticulated domes subjected to impact and the judgment [J].Thin-Walled Structures,2010,48(2):143- 149.

[4] 王多智.冲击荷载下网壳结构的失效机理研究 [D].哈尔滨:哈尔滨工业大学,2010.

[5] 马肖彤,王秀丽.冲击荷载作用下单层网壳结构动力稳定性研究 [J].振动与冲击,2015,34(2):119- 124. MA Xiao-tong,WANG Xiu-li.Dynamic stability of single-layer reticulated shell structure subjected to impact loads [J].Journal of Vibration and Shock,2015,34(2):119- 124.

[6] OSHIRO R E,ALVES M.Scaling of structures subject to impact loads when using a power law constitutive equation [J].International Journal of Solids and Structures,2009,46(18/19):3412- 3421.

[7] OSHIRO R E,ALVES M.Predicting the behaviour of structures under impact loads using geometrically distorted scaled models [J].Journal of the Mechanics and Physics of Solids,2012,60(7):1330- 1349.

[8] OSHIRO R E,ALVES M.Scaling of cylindrical shells under axial impact [J].International Journal of Impact Engineering,2007,34:89- 103.

[9] 秦健,张振华.原型和模型不同材料时加筋板冲击动态响应的相似预报方法 [J].爆炸与冲击,2010,30(5):511- 516. QIN Jian,ZHANG Zhen-hua.A scaling method for predicting dynamic responses of stiffened plates made of mate-rials different from experimental models [J].Explosion and Shock Waves,2010,30(5):511- 516.

[10] 迟世春,林少书.结构动力模型试验相似理论及其验证 [J].世界地震工程,2004,20(4):11- 20. CHI Shi-chun,LAM Siu-shu.Validation of similitude laws for dynamic structural model test [J].World Earthquake Engineering,2004,20(4):11- 20.

[11] TRIMINO L F,CRONIN D S.Non-direct similitude technique applied to the dynamic axial impact of bonded crush tubes [J].International Journal of Impact Engineering,2014,64:39- 52.

[12] 余同希,卢国兴.材料与结构的能量吸收 [M].北京:化学工业出版社,2005.

[13] 叶继红,潘锐.单层球壳模型结构振动台试验研究 [J].建筑结构学报,2013,34(4):81- 90. YE Ji-hong,PAN Rui.Shaking table test on collapse process of single-layer spherical shells [J].Journal of Building Structures,2013,34(4):81- 90.

[14] 聂桂波,范峰,支旭东,等.单层球面网壳结构失效机理振动台试验 [J].土木工程学报,2013,46(10):17- 25. NIE Gui-bo,FAN Feng,ZHI Xu-dong,et al.Shaking table test on failure mechanism of single-layer reticulated dome [J].China Civil Engineering Journal,2013,46(10):17- 25.

[15] 吴长.强震与冲击荷载下球面网壳的动力失效分析与试验研究 [D].兰州:兰州理工大学,2014.

Gravity-Based Impact Comparability Rule of Single-Layer Reticulated Shells and Its Numerical Verification

JIANGZheng-rong1,2ZHONGYu-kai1SHIKai-rong1,2LUOBin3

(1.School of Civil Engineering and Transportation,South China University of Technology,Guangzhou 510640, Guangdong,China;2.State Key Laboratory of Subtropical Building Science,South China University of Technology,Guangzhou 510640,Guangdong,China;3.School of Civil Engineering, Southeast University,Nanjing 211189,Jiangsu,China)

Through the dimensional analysis,a comparability rule expression of single-layer reticulated shells subjected to a vertex impact is derived in this paper,which considers the gravity and the strain-rate effect of relevant materials.On this basis,two methods of preparing material specially and adding extra mass are proposed to meet the scaling requirements.Then,a model according well with available literaturesis constructed by using the nonlinear finite element software LS-DYNA,and it is proved to be reliable by comparing the experimental results withthe simulation ones.Finally,two analytical models of Kiewitt-Lamella single-layer reticulated shells are respectively constructed to verify the proposed two methods by comparing their node displacements.The results show that the proposed two methods can both accurately predict the displacement of the prototype,with the relative error absolutes of less than 15% and 12% respectively,and they can both accurately predict the collapse modes of the prototype,especially the whole collapse,and that the method of adding extra mass is better in terms of precision and maneuverability.

comparability rule; strain-rate effect; gravity; single-layer reticulated shell

2015- 10- 08

国家“十二五”科技支撑计划项目(2012BAJ03B06)；广州市科技计划项目(1563000257) Foundation item: Supported by the National Key Technology Research and Development Program of the Ministry of Science and Technology of China during the “12th Five-Year Plan”(2012BAJ03B06)

姜正荣(1971-)，男，博士，副教授，主要从事大跨度空间结构研究.E-mail：zhrjiang@scut.edu.cn

† 通信作者: 石开荣(1978-)，男，博士，副教授，主要从事预应力钢结构研究.E-mail:krshi@scut.edu.cn

1000- 565X(2016)10- 0043- 06

O 383

10.3969/j.issn.1000-565X.2016.10.007