基于谐波小波和SVD的可倾瓦滑动轴承工频干扰抑制*
2017-01-05张晓涛李伟光
张晓涛 李伟光
( 华南理工大学 机械与汽车工程学院, 广东 广州 510640 )
基于谐波小波和SVD的可倾瓦滑动轴承工频干扰抑制*
张晓涛 李伟光
( 华南理工大学 机械与汽车工程学院, 广东 广州 510640 )
针对新型流体支撑可倾瓦滑动轴承的振动位移信号中的工频干扰问题,提出了基于谐波小波和奇异值分解(SVD)的工频干扰抑制算法.首先基于谐波小波的严格盒型频谱和任意频段任意细分的特性,提取包含工频频谱的频段,然后在时域构建Hankel矩阵并进行奇异值分解,将反映工频成分的特征值置零,从而抑制工频成分,最后将去除工频的子带频谱同原始频谱其他子带合并,得到去除工频干扰的有用信号用于后续分析.试验结果表明,此算法可有效抑制工频干扰,为后续的新型可倾瓦滑动轴承的振动特性研究奠定基础,具有一定的工程应用价值.
谐波小波;奇异值分解;工频干扰;可倾瓦滑动轴承
可倾瓦滑动轴承中的各瓦块独立地绕支点自由摆动以适应运转条件的变化,具有较好的稳定性,在汽轮机和风机等行业中获得了广泛的应用[1].但是传统的可倾瓦滑动轴承存在一定缺陷,由于其采用机械支点方式使得轴承系统运行稳定性下降,支点产生磨损,因此需要研究新型的可倾瓦滑动轴承[2].
新研制的三瓦可倾瓦滑动轴承用流体支撑取代机械支点,并搭建大型试验台用于轴承振动性能的试验研究.采用电涡流位移传感器测量可倾瓦滑动轴承转子轴颈处的振动位移时,发现采集的信号中存在较强的工频干扰.工频干扰会在时域波形和轴心轨迹上反映出来,影响信号的分析和判断,因此需要研究合适的抑制方法.
工频干扰尽管成分简单,但由于其频带分布与有用信号频率成分经常互相混叠,用常规滤波方法难以有效消除工频干忧.目前广泛应用的工频干扰抑制方法有[3]:陷波器法;工频回归相减抑制法;基于同步测量工频参考源的自适应滤波法(简称自适应滤波法).从滤波效果和保护有用信号成分两方面因素考虑,工频回归相减抑制法效果相对较好,但该方法需要对工频干扰的相位和幅度进行精确估计,在实际应用中存在一定困难.自适应滤波法作为工频回归相减抑制法的扩展,在工程应用中要求同步测量工频参考信号,同时滤波器系数的调整需要一定时间才能进入稳态,所以对非平稳性很强的信号难以保证其效果.
此外,独立分量分析(ICA)和小波分析在工频干扰抑制方面都有广泛应用.ICA算法[4- 5]要求观测信号数目大于或等于独立源数目,否则难以获得较好的信号分离效果.而小波分析[6]方法是基于小波的多分辨率特性,将信号分解到不同频带,采用阈值法去除工频成分.此方法会对同一频带内的有用信号造成干扰.
谐波小波在信号处理领域得到广泛应用[7],它除具有通常意义下的小波的特点外,还具有自身的特性:明确的数学表达式、极好的“盒形”频谱、完美的滤波特性以及零相位特性,可有效提取微弱特征信号[8].SVD是一种正交变换,它将原矩阵转化为一个对角矩阵,得到的原矩阵的奇异值可以有效反映原矩阵中的一些特征,在机械振动信号处理领域得到了广泛的应用[9].小波变换和SVD 这两种方法的结合在信号处理、故障诊断和参数识别等领域表现出了独特的优势[10].因此,文中将这两种方法相结合用于工频干扰抑制,提出基于谐波小波-SVD的工频干扰抑制算法.其先对信号进行傅里叶变换,将目标定位在一个可伸缩的较小区域内并提取出来,采用逆傅里叶变换以得到包含目标信号的时域数据,再构造为Hankel矩阵并应用奇异值分解方法消除工频干扰,最后进行信号重构得到时域信号,并与常用的陷波器滤波方法进行比较.
1 流体支撑可倾瓦滑动轴承原理
可倾瓦滑动轴承 (如图1所示)瓦块能够绕机械支点摆动,自由调整位置形成油楔,以适应转速、轴承负载等的变化,瓦块内的油膜压力的合力都通过轴颈中心,具有较好的稳定性,在大型旋转机械上获得广泛应用.为克服传统可倾瓦滑动轴承的缺陷,文中设计了流体支承的可倾瓦滑动轴承,将机械支点改进为流体支撑,利用流体来支撑轴瓦,增加轴瓦自由度并减少轴瓦的振动[11].图1中,ω为角频率,O为支点中心,J为轴颈中心.

图1 可倾瓦滑动轴承模型
新研制的轴承具有双层油膜结构,如图2所示.内层油膜为动压油膜,在工作条件下,轴颈处于流体动压润滑状态,利用流体的动压润滑原理,形成具有承载力的油膜.轴瓦中心位置的静压孔与轴瓦背面的静压腔连通,其中部分动压润滑油经静压孔进入轴瓦背面的静压腔内产生静压力,当静压力足够大时,将轴瓦浮起,从而在轴瓦外表面形成外层油膜.可倾瓦滑动轴承内层油膜与外层油膜共同产生阻尼减振作用.内层油膜为流体动压油膜阻尼减振,外层油膜为静压油膜与挤压油膜,内、外层油膜相互联系、共同作用,同时存在着能量耗散,减小振动.
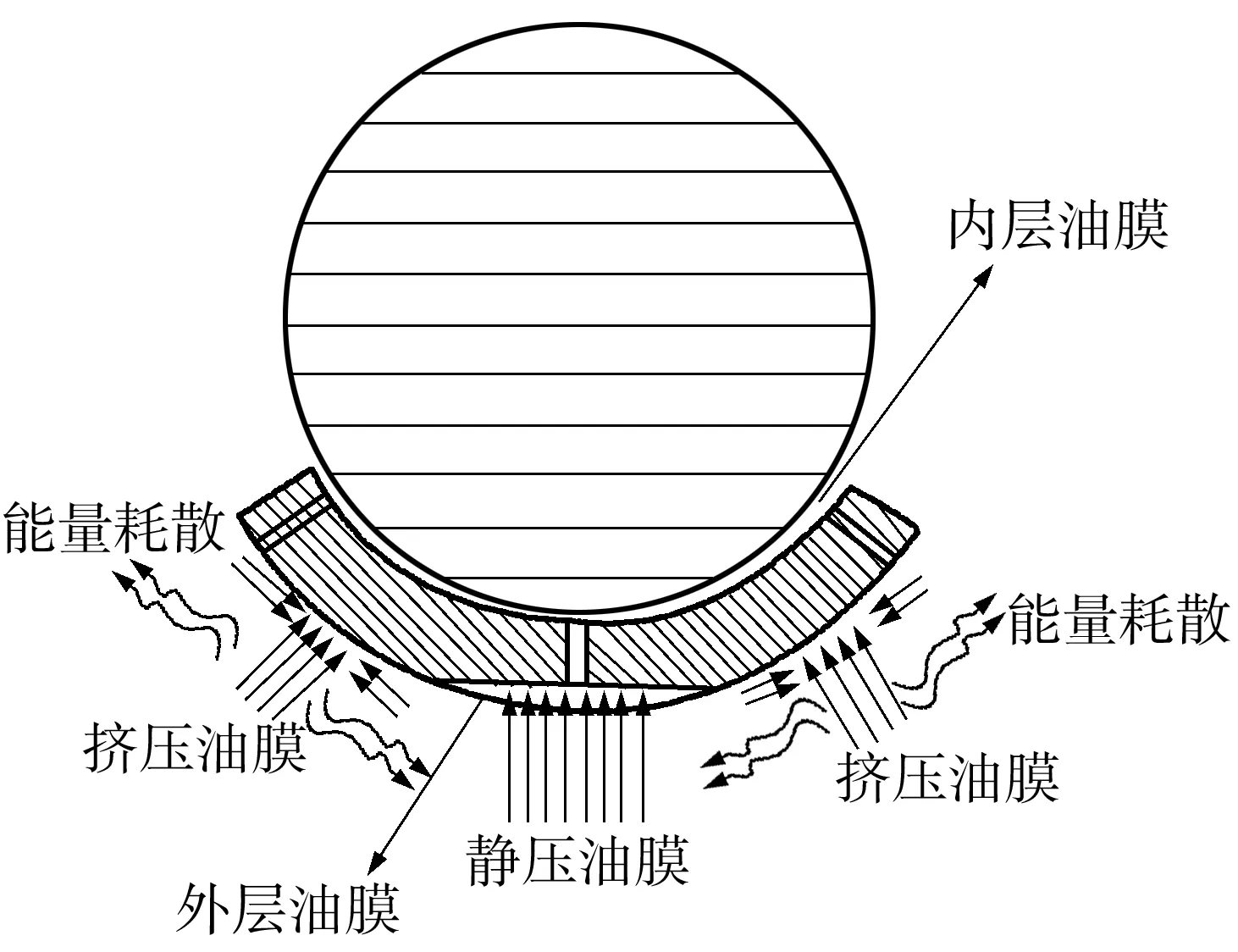
图2 轴承油膜结构
2 可倾瓦滑动轴承试验台
为测试新研制的流体支撑可倾瓦滑动轴承的振动性能,搭建可倾瓦滑动轴承试验台,其示意图如图3所示,实物如图4所示.

图3 试验台示意图

图4 试验台实物
整个试验台包括:基座、转子、大功率伺服电机及其机架、连接电机和前轴承的联轴器、控制转子轴向位移的推力轴承及推力轴承座、给可倾瓦轴承供油的稀油站及前、后可倾瓦滑动轴承等.
采用Kaman KD2306-1S电涡流位移传感器测量轴颈处的振动位移,传感器量程为1 mm,分辨率为0.1 μm.传感器安装如图5所示.

图5 电涡流传感器
3 谐波小波和SVD方法
3.1 谐波小波
经典谐波小波[7]最早是由Newland提出的,其频域表达式定义为
(1)
式中:ω为角频率;m、n决定了谐波小波变换的尺度j,j∈Z+,n=2j+1,m=2j.谐波小波在相应频带内具有恒定的幅值,而在频带外为0.
谐波小波在时域的表达式为
(2)
从式(2)可见,谐波小波是实部为偶函数而虚部为奇函数的复小波,具有零相移特性.
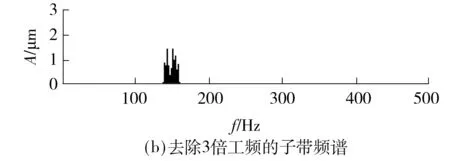
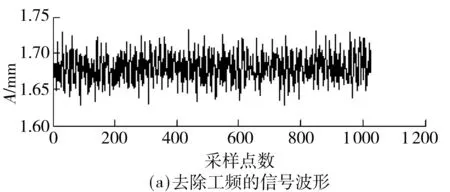
式(1) 中定义的谐波小波称为二进谐波小波,其频带划分不均匀,低频段较细,高频段较粗.Newland[12- 13]重新定义m、n的取值:m,n∈R+且m 将ψm,n(t)以步长k/(n-m)进行平移,式(2)变为广义谐波小波的一般表达式: (3) 在无交叠的情形下,不同频带对应的小波是正交的;相同频带而 k不同时,其所对应的小波也是正交的.以谐波小波函数系ψm,n(t)作为L2(R)的一组正交基,对信号做谐波小波分解,可将信号无交叠、无遗漏地分解到相互独立的频带内. 3.2SVD理论 实矩阵A∈Rm×n,存在正交矩阵U∈Rm×m和V∈Rn×n,使得式(4)成立: A=UDVT (4) 其中,D为对角阵,D=diag((δ1,δ2,…,δr),Ο),Ο表示零矩阵,r=min(m,n),δ1≥δ2≥…≥δr,δ1,δ2,…,δr称为A的奇异值. SVD可表示为r个秩为1的m×n阶子矩阵的和的形式,如式(5)所示: (5) 式中,ui和vi分别为矩阵的第i个列向量;δi为矩阵A的第i个奇异值.式(5)表明,矩阵A可分解为r个相互正交的子空间,从而将矩阵包含的信息分解到不同的子矩阵. 基于相空间重构理论,信号x(l)(l=0,1,…,N-1),将其构造Hankel矩阵 (6) 利用式(4)进行奇异值分解,将反映工频信息的奇异值置零,利用式(5)重构矩阵,将矩阵中相应的项相加还原出信号,同时去除工频干扰. 文献[14- 15]的研究表明:r越大,则原始信号中各分量的分离效果越好.工程应用中一般取r=N/2(当N不是偶数时,舍弃最后一个数据点). 3.3 谐波小波-SVD算法 对离散时间信号x(l),采样率为fs.谐波小波-SVD算法的实现流程如下: (1)根据先验知识及目标子带的带宽fbw和中心频率fc,计算子带的上限和下限: (7) (2)计算各子带的广义谐波小波的频域表达式: (8) (3)对信号进行快速傅里叶变换(FFT),得到频谱X(f)(f=0,1,2,…,N-1). (4)计算目标子带的频谱: (9) (10) 式(10)表明:各个子带分量相加可重构原信号.除目标子带外,其余频谱表示为X′(f). (5)对式(10)求逆傅里叶变换, (11) (6)按照式(4),对xm,n(t)构造Hankel矩阵,并进行奇异值分解,得到一组非零奇异值,将反映工频信息的奇异值置零,即达到抑制工频成分的目的. (8)将去除干扰的各目标子带和X′(f)合并 (12) 对X″(f)作逆傅里叶变换,得到去除工频干扰的信号x′(t).算法结束. 谐波小波-SVD算法可以概括为:先用谐波小波定位,再用SVD进行工频干扰抑制. 采用比利时LMS数据采集系统,数据采集硬件和软件:LMSSCADAS和LMSTest.Lab14A.将试验台转子工作转速设定为3 840r/min(64Hz),采样率为fs=1 024Hz,采集信号长度N=1 024. 采集信号的时域波形及其频谱如图6所示,其中A为幅值.由于直流分量数值较大,为方便显示交流分量,图6(b)中未给出直流成分频谱.由时域波形图及频谱图可见,在可倾瓦滑动轴承系统工作过程中,试验台具有非常复杂的振动特性.时域波形图中由于噪声很强,信号完全被淹没,根本看不出转子的振动特性.频谱图中则体现为:转频及其谐波成分、50Hz工频及其谐波成分以及其他频率成分.因此,为了分析可倾瓦滑动轴承的振动特性,必须先将50Hz工频及其谐波去除,然后再进行后续的分析. 图6(b)中标明了50Hz工频及其谐波(1X-5X),其中1X、3X频率较为明显,文中着重去除这2个频率成分. 图6 信号时域波形和信号频谱 根据谐波小波-SVD算法的第(1)步:确定目标子带中心频率fc和带宽fbw.带宽选取的原则:将fc限定在一个相对小的区域,突出fc,其他频率成分相对较小,以便于应用奇异值分解方法处理.工频为50 Hz,3倍工频为150 Hz,则fc=50k(k=1,3),当fbw=20 Hz时可以满足要求.根据式(3)计算子带下限和上限:当fc=50 Hz时,(m,n)=(40,60);当fc=150 Hz时,(m,n)=(140,160). 根据谐波小波-SVD算法第(2)-(4)步,从信号频谱中提取50 Hz工频子带如图7(a)所示、150 Hz 3倍工频子带如图7(b)所示.图中,50、150 Hz都为最主要的频谱.为将fc去除,如果采用陷波滤波器,则除了将fc去除,还会将与其邻近的频谱也去除,从而影响信号完整性,不利于后续的分析.这里采用奇异值分解方法,去除的只是fc,对邻近信号无影响. 图7 工频及3倍工频子带 根据谐波小波-SVD算法的第(5)步,将上述子带进行逆傅里叶变换,得到时域值,其波形如图8所示. 图8 工频子带和3倍工频子带时域波形 Fig.8 Waveform of power frequency and triple power frequencysub-bands 根据谐波小波-SVD算法的第(6)步,对所得时域信号构造Hankel矩阵并进行奇异值分解,得到的奇异值谱如图9所示. 图9 工频子带和3倍工频子带奇异谱 Fig.9 Singular values spectrum of power frequency and triple power frequency sub-bands 根据奇异值分解理论,50 Hz子带的奇异值序列中的第1和第2个奇异值代表50 Hz成分,150 Hz子带的奇异值序列中第1和第2个奇异值代表150 Hz成分,将二者的第1和第2个奇异值都置零,然后按式(5)进行重构得到时域信号.根据谐波小波-SVD算法的第(7)步,对时域信号做FFT,得到的频谱如图10所示. 图10 去除工频和3倍工频的子带频谱 Fig.10 Sub-band spectrum with power frequency and triple power frequency removed 比较图10(a)和图7(a),图10(b)和图7(b)可以看到工频及其3倍工频都得以完整去除. 根据谐波小波-SVD算法的第(8)步,得到去除工频干扰后的时域波形如图11(a)所示,及其频谱如图11(b)所示,图中标明了转频(64 Hz)及其倍频(1X-5X). 图11 去除工频的信号波形和频谱 Fig.11 Waveform and frequency spectrum with power frequency removed 比较图11(a)和图6(a),图11(b)和图6(b),可见,经过谐波小波-SVD算法的处理后,去除了50 Hz工频及其3倍工频成分的干扰,得到以转频64 Hz及其倍频为主的信号,从而可以在此基础上对信号进行转子质量不平衡、转子不对中、碰磨、油膜涡动等各种振动特征分析. 作为对比,这里给出常用陷波器的滤波结果.根据无限冲击响应(IIR)数字滤波器理论[16],50 Hz陷波器的传递函数为 (13) 经陷波器滤波后的信号频谱如图12所示.比较图12和图11(b)可以发现,经陷波器滤波后,不但基频信号幅值下降,而且在滤除50Hz频谱和150Hz频谱的同时,将其相邻的部分有用信号同时滤掉了,从而会导致信号受损.这表明,文中提出的谐波小波-SVD算法较常用的陷波器滤波方法有明显的优势. 图12 陷波器滤波后信号频谱 针对电涡流位移传感器采集信号中的工频干扰问题,提出了基于谐波小波-SVD的干扰抑制算法,并将其应用在新型流体支撑可倾瓦滑动轴承振动特性的试验研究中,既去除了工频成分又不影响有用信号,有利于后续研究.且同常用陷波器滤波方法相比具有明显优势,这表明所提出的算法具有一定的工程应用价值.文中对工频及其倍频的子带宽度的选择是人为进行的,而自适应方式的子带宽度选择会更加地合理、有效,因此后续需要继续研究子带宽度和信号特征的关系,以实现子带宽度选择的自适应性. [1] 李伟光,彭喆,周平.可倾瓦滑动轴承的静态性能分析 [J].润滑与密封,2013,38(8):6- 12. LI Wei-guang,PENG Zhe,ZHOU Ping.Analysis on static performance of tilting-pad journal bearing [J].Lubrication Engineering,2013,38(8):6- 12. [2] 周利俊.油膜轴承试验台系统研制 [D].广州:华南理工大学,2013. [3] 张营,左洪福,佟佩声,等.基于谱插值和奇异值差分谱的滚动轴承静电监测信号去噪方法 [J].航空动力学报,2014,29(8):1996- 2002. ZHANG Ying,ZUO Hong-fu,TONG Pei-sheng,et al.De-noising method for electrostatic monitoring signal of roller bearing based on spectrum interpolation and difference spectrum of singular value[J].Journal of Aeronautics,2014,29(8):1996- 2002. [4] 敖春来,邹连亮,姜晓军,等.基于独立分量分析的自然电位测井曲线工频干扰消除 [J].西部探矿工程,2014(1):105- 110. AO Chun-lai,ZOU Lian-liang,JIANG Xiao-jun,et al.Power frequency interference removal for natural potentiallogging curve based on ICA [J].West-China Exploration Engineering,2014(1):105- 110. [5] 席旭刚,朱海港,高发荣,等.匹配滤波和ICA消除触觉传感器工频噪声 [J].中南大学学报(自然科学版),2013,44(2):145- 149. XI Xu-gang,ZHU Hai-gang,GAO Fa-rong,et al.Power frequency noise reduction technique of tactile sensor signal using matched filter and ICA [J].Journal of Central South University(Science and Technology),2013,44(2):145- 149. [6] 蔡剑华,李晋.基于频率域小波去噪的大地电磁信号工频干扰处理 [J].地质与勘探,2015,51(2):353- 359. CAI Jian-hua,LI Jin.Suppression of power line interference on MT signals based on the frequency domain wavelet method [J].Geology and Exploration,2015,51(2): 353- 359. [7] LIU B.Adaptive harmonic wavelet transform with applications in vibration analysis [J].Journal of Sound and Vibration,2003 (262):45- 64. [8] NEWLAND D E.Harmonic wavelet analysis [J].Proceedings of the Royal Society London,1993,443(10):203- 225. [9] 唐炬,董玉林,樊雷,等.基于Hankel矩阵的复小波_奇异值分解法提取局部放电特征信息 [J].中国电机工程学报,2015,35(7):1808- 1817. TANG Ju,DONG Yu-lin,FAN Lei,et al.Feature information extraction of partial discharge signal with complex wavelet transform and singular value decomposition based on Hankel matrix [J].Proceedings of the CSEE,2015,35(7):1808- 1817. [10] 赵学智,陈统坚,叶邦彦.基于小波-奇异值分解差分谱的弱故障特征提取方法 [J].机械工程学报,2012,48(2):37- 48. ZHAO Xue-zhi,CHEN Tong-jian,YE Bang-yan.Extraction method of faint fault feature based on wavelet-SVD difference spectrum [J].Journal of Mechanical Engineering,2012,48(2):37- 48. [11] 周平.流体支承可倾瓦滑动轴承系统的设计与性能研究 [D].广州:华南理工大学,2012. [12] NEWLAND D E.Wavelet analysis of vibration(Part 1):theory [J].Journal of Vibration and Acoustics,Transactions of the ASME,1994,116(10):409- 416. [13] NEWLAND D E.Ridge and phase identification in the frequency analysis of transient signals by harmonic wavelets [J].Journal of Vibration and Acoustics,Transactions of the ASME,1999,121(2):149- 155. [14] 钱征文,程礼,李应红.利用奇异值分解的信号降噪方法 [J].振动、测试与振动,2011,31(4):459- 463. QIAN Zheng-wen,CHENG Li,LI Ying-hong.Signal de-noising method using SVD [J].Journal of Vibration,Measurement & Diagnosis,2011,31(4):459- 463. [15] 胥永刚,孟志鹏,陆明,等.双树复小波和奇异差分谱在滚动轴承故障诊断中的应用 [J].振动工程学报,2013,26(6):965- 973. XU Yong-gang,MENG Zhi-peng,LU Ming,et al.Application of dual-tree complex wavelet transform and singular value difference spectrum in the rolling bearing fault diagnosis [J].Journal of Vibration Engineering,2013,26(6): 965- 973. [16] 王立会,潘冬明.一种消除心电信号中工频干扰的陷波器设计 [J].医疗设备信息,2007,22(7):18- 20. WANG Li-hui,PAN Dong-ming.Design of digital trap for eliminating power-line interference on ECG signals [J].Information of Medical Equipment,2007,22(7):18- 20. Power Interference Removal of Tilting-Pad Journal Bearing Based on Harmonic Wavelet and SVD ZHANGXiao-taoLIWei-guang (School of Mechanical and Automotive Engineering, South China University of Technology,Guangzhou 510640, Guangdong,China) In order to remove the power interference in the vibration displacement signals of a novel tilting-pad journal bearing with fluid pivot, a power interference removal algorithm based on the harmonic wavelet and the singular value decomposition (SVD) is proposed. In the algorithm, first, the frequency domain containing the power frequency is extracted by using the harmonic wavelet that has strict box-like spectrum and arbitrary detail of arbitrary frequency domain. Then, a Hankel matrix is constructed in the time domain, the singular value decomposition is performed, and the singular values relevant to the power frequency are set to be zero, thus removing the power frequency. Finally, all the sub-bands without power frequency are merged with the other sub-bands of the original frequency spectra. Thus, the time domain signals without the power interference are achieved for a further study. Experiment results show that the proposed algorithm can effectively remove the power interference. This algorithm helps to investigate the vibration characteristic of the novel tilting-pad journal bearing, and it is both practical and feasible. harmonic wavelet; singular value decomposition; power interference; tilting-pad journal bearing 2016- 01- 11 国家高技术研究发展计划(863计划)项目(2015AA043005);南沙区科技计划项目(2014CX07) Foundation item: Supported by the National High-tech R&D Program of China(863 Program)(2015AA043005) 张晓涛(1973-),男,博士生,主要从事旋转机械故障诊断研究.E-mail:1792654107@qq.com 1000- 565X(2016)10- 0001- 07 TH 117.2;TH 113.1 10.3969/j.issn.1000-565X.2016.10.001
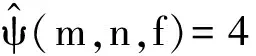


4 试验数据采集与分析
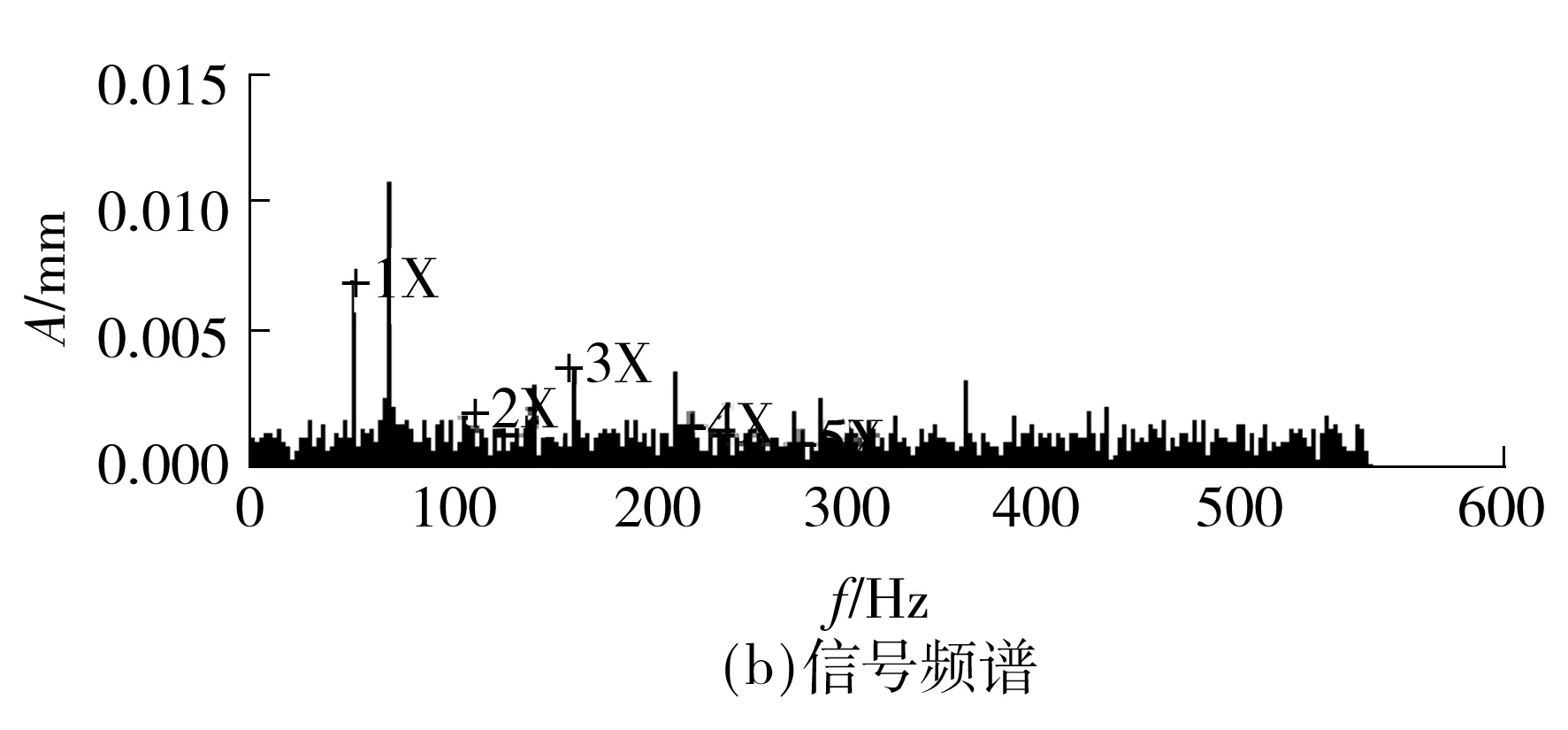
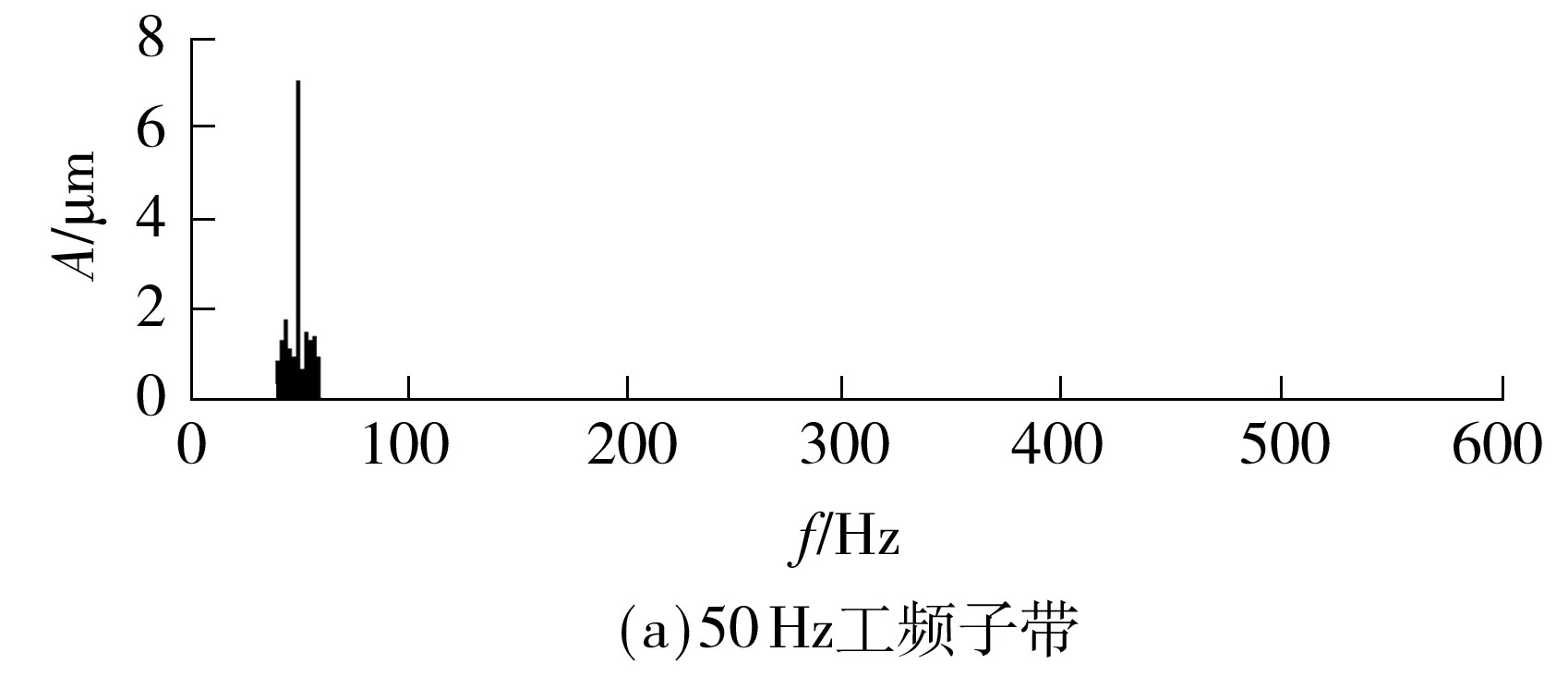


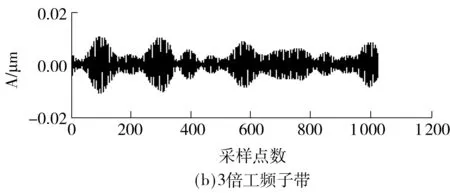
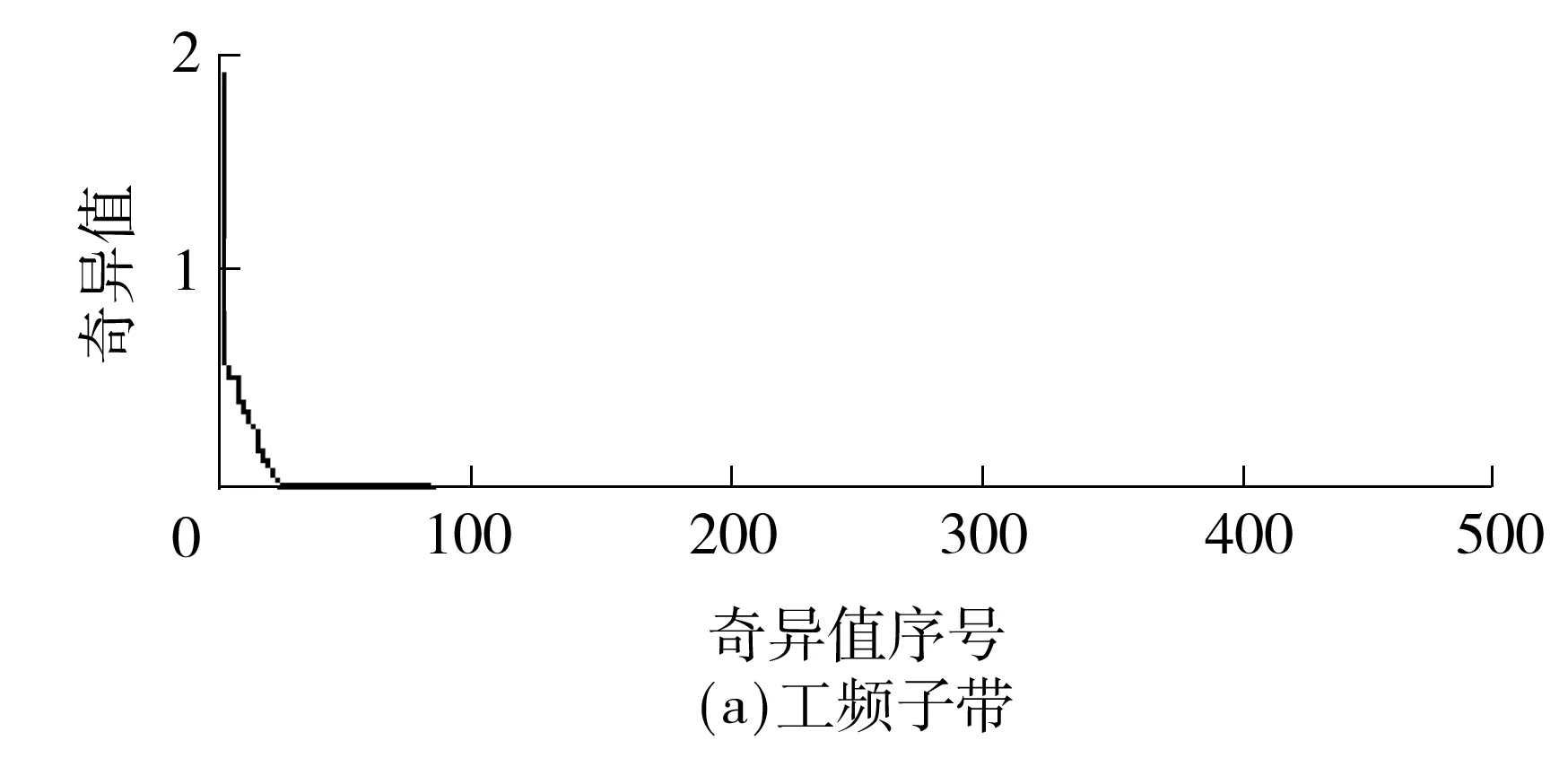



5 常用陷波器的处理效果


6 结语
