静水压荷载下功能梯度圆环的弹性屈曲*

黄怀纬 张永强,2 韩强

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.广州打捞局， 广东 广州 510260)

静水压荷载下功能梯度圆环的弹性屈曲*

黄怀纬1张永强1,2韩强1

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.广州打捞局， 广东 广州 510260)

管道屈曲问题中，结构通常被考虑为平面应力圆环，但若存在轴向位移约束，其状态更接近平面应变圆环的状态.文中从理论上研究静水压作用下平面应力和平面应变功能梯度材料圆环的弹性屈曲问题.假定材料沿厚度方向弹性物性按照幂律分布连续变化，结合一阶剪切变形理论和Kárman几何关系，应用虚位移原理，导出结构的基本平衡方程；采用本征值方法得到了屈曲控制方程和结构屈曲临界荷载的解析解.通过算例比较了平面应力和平面应变状态下结构理论屈曲性能，同时考察了结构径厚比和材料组分参数的影响.结果表明：平面应变功能梯度材料圆环屈曲临界荷载略高于平面应力的结果；当材料组分参数介于0.1至10区间内时，两种圆环的屈曲临界荷载均下降得较为明显.

功能梯度材料；圆环；屈曲；虚位移原理

1984年日本学者提出了功能梯度材料(FGMs)[1]，它是一种新型的陶瓷/金属共混复合材料.这一材料具有连续过渡的材料物性，能有效缓解由于物性不连续引发的应力集中现象，避免了材料的断裂和脱层破坏.

圆环结构作为海底油气管道及潜艇的基础力学模型，其在静水压下的稳定性能备受关注.早期相关的研究主要是Timoshenko等[2]针对弹性薄圆环结构线性屈曲问题提出的理论解析解.Flaherty等[3]和Hodges等[4]则引入几何非线性效应，建立了匀质圆环非线性大变形理论，并研究了圆环的后屈曲大变形问题.此外，在复合材料圆环屈曲方面，Kim等[5]针对叠层复合材料圆环提出了结构的屈曲临界荷载的解析解.

近20年来，针对FGM梁、板、壳等结构的力学研究层出不穷，特别是在结构弹性屈曲研究领域已取得诸多成果[6- 11].对于FGM圆环，Kerdegarbakhsh等[12]讨论了平面应力状态下结构的后屈曲行为.尽管如此，对于FGM圆环结构屈曲问题的研究仍不多见.文中以FGM圆环为研究对象，比较了平面应力和平面应变状态下FGM圆环的屈曲性能，同时考察了结构的径厚比和材料的组分参数对结构屈曲性能的影响.

1 问题描述

考虑FGM圆环结构的面内屈曲问题，结构厚度为h，中面半径为R，r和θ表示径向和圆环坐标轴，z为厚度方向上的坐标轴，x轴则指向圆环平面的法向方向，如图1所示.坐标系原点位于圆环中面，因此有z=r-R.

FGMs是由陶瓷相和金属两相共混复合而成的新材料，其组分比在厚度方向上是变化的，使得其材料物理性质也在厚度方向上有所不同.为了描述陶瓷/金属共混材料的材料物性，通常可以采用线性混合律[7].这是一种简单实用的方法，其将FGMs的弹性模量和泊松比取为各相属性的权平均，即

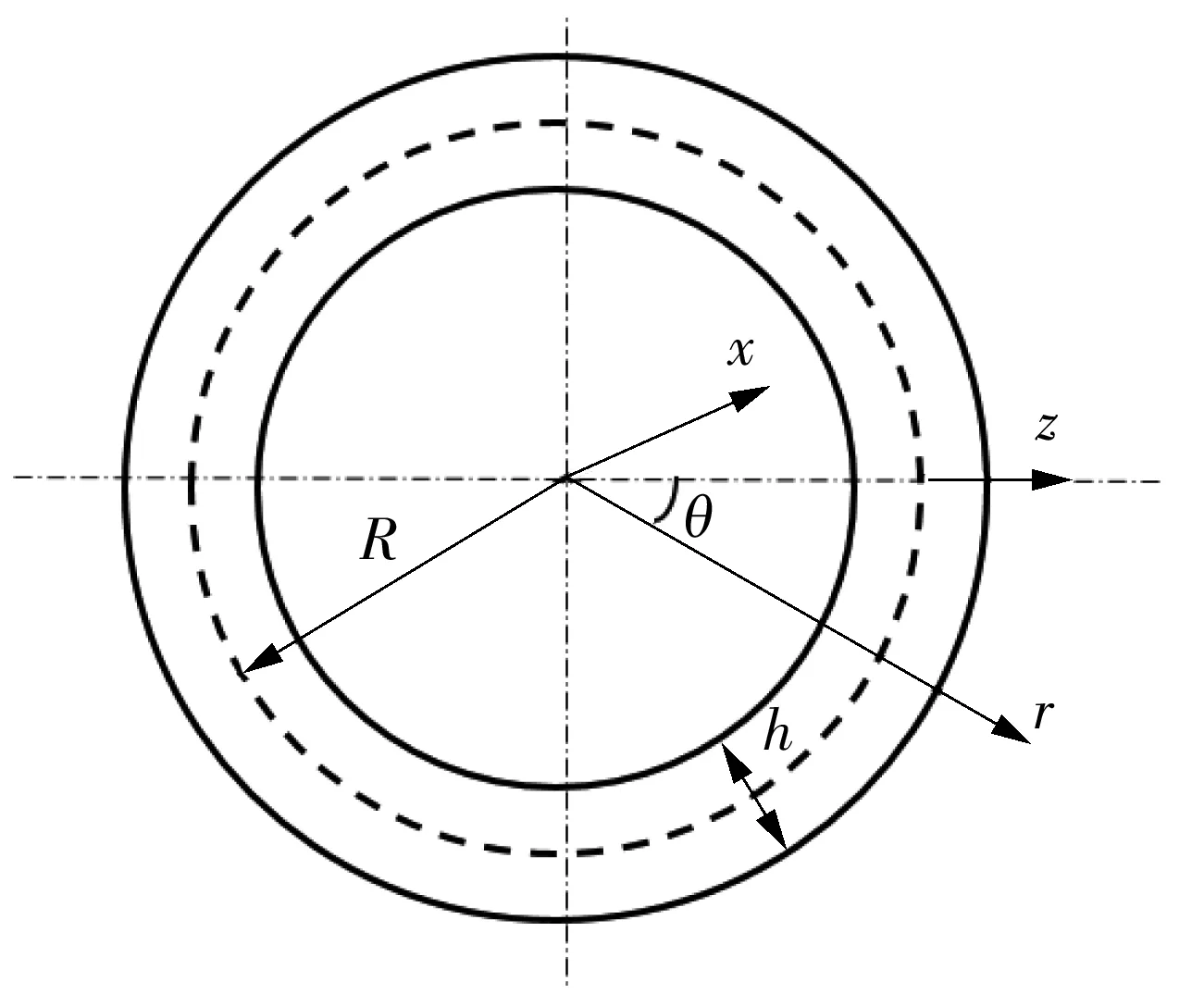
图1 FGM圆环的尺寸参数及坐标系统

(1)

式中,E、ν、φ分别表示弹性模量、泊松比和组分体积分数，下标c,m分别对应陶瓷相和金属相材料.

假设陶瓷组分的体积分数满足幂率分布特征[13]，同时假设陶瓷和金属混合材料不含任何孔隙，可以给出陶瓷相和金属相组分体积分数φc、φm满足以下关系：

(2)

其中：k为材料组分参数，它表征了组分材料的空间分布情况或材料的不均匀程度；z=0对应于材料中面，z=±h/2对应于材料的陶瓷表面和金属表面，即各材料点位置位于-h/2≤z≤h/2的范围内.通过变化材料组分参数，FGM中各组分体积分数沿厚度连续变化，进而实现物性的连续过渡.

2 公式推导

2.1 材料本构关系

材料的本构模型可写成

(3)

管道属于长圆柱壳结构，根据管道固定方式不同，可以将管道简化为两种极端的力学模型，即平面应力圆环和平面应变圆环.对于平面应变圆环有εxx=0，对于平面应力圆环有σxx=0，式(3)均可简化为

(4)

其中,

2.2 剪切变形理论

圆环结构的非线性几何关系为[14]

(5)

这一关系是Von-Kárman类型的应变-位移关系，下标中逗号表示偏导数.根据一阶剪切变形理论，环向位移V(θ,z)和径向位移W(θ,z)由下式给定:

(6)

其中，v(θ)、w(θ)分别为中面环向和径向的位移，φ(θ)为中面转角.一般来说，r≈R且z/R≪1，同时φ小于径向位移w所引起的转角，即w′/R，因此应变分量可表示为

(7)

圆环环向内力和剪力N、Q以及内力矩M由下式给出:

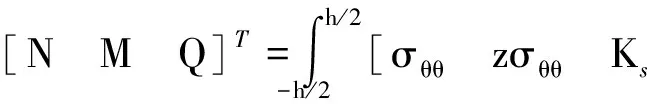
(8)

其中，Ks为剪切矫正因子，根据一阶剪切变形理论，可取值为5/6.

将式(7)代入(8)得到

(9)

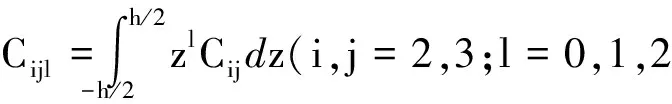
2.3 平衡方程

圆环的虚内能δUin表示为

(10)

其中，b为圆环沿x方向上的厚度，若圆环外部压力方向总是垂直于变形后的圆环法向，即外部荷载为静水压力q，则由于外力所引起的虚势能(负虚功)δUex[15]可表示为

(11)

根据虚位移原理，系统处于平衡状态时，虚势能δU必须为零，结合式(10)和(11)有

(12)

上述方程在任意虚位移δw,δv,δφ的情况下均必须满足F=0，因此，通过分部积分的处理方法，可以得到圆环的基本平衡方程.

(13)

其中，求导符号“′”表示对变量θ求导数.由于圆环环向闭合的周期条件，分部积分所产生的全积分项必须满足以下关系：

(14)

2.4 屈曲控制方程

将圆环位移、内力、内力矩及剪力化为前屈曲量与屈曲量的叠加.

(15)

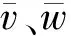
由此，FGM圆环的屈曲控制方程可以写成

(15)

将式(7)第二式和式(9)写成屈曲位移增量形式，得到内力、剪力、内力矩的增量表达式

(16)

将式(16)代入式(15)，且忽略非线性项的影响，则给出了以屈曲位移增量表示的线性屈曲控制方程.

(17)

3 屈曲分析

假设圆环的屈曲位移增量写成如下形式：

(18)

其中，ξw、ξv、ξφ分别为屈曲位移的幅值，n为屈曲波形参数.将式(18)代入式(17)得到关于ξw、ξv、ξφ的线性方程组:

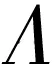
(19)

其中：

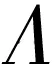
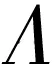
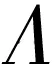
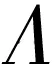
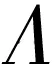
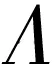
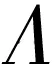
(20)

将上式退化为匀质弹性圆环的情况，并忽略小项2(1+ν)(h/R)2的影响，可得

(21)

4 算例及结果

该部分计算选用温度T=300K下Si3N4/SUS304FGM[7]的材料属性，其组分材料的材料属性为Ec=348.43GPa,Em=201.04GPa,νc=0.240,νm=0.326.

设定材料组分参数k=1，表1给出了径厚比(R/h)在100至500区间内FGM圆柱壳的平面应力和平面应变状态下的弹性屈曲临界荷载.将表1的数据绘于图2，可以看出，平面应变结果普遍略高于平面应力的结果，同时，FGM圆柱壳的屈曲临界荷载随着径厚比R/h的增大显著降低.

表1 不同径厚比FGM圆环的屈曲临界荷载

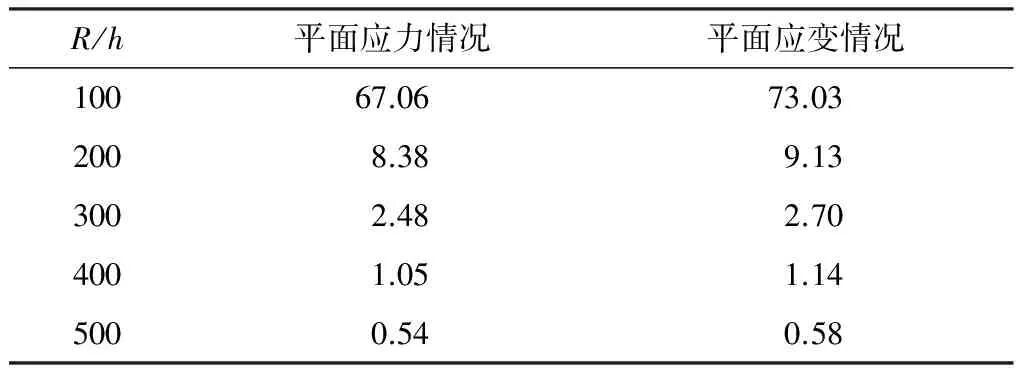
Table 1 Critical load of FGM rings with different radius-to-thickness ratioskPa

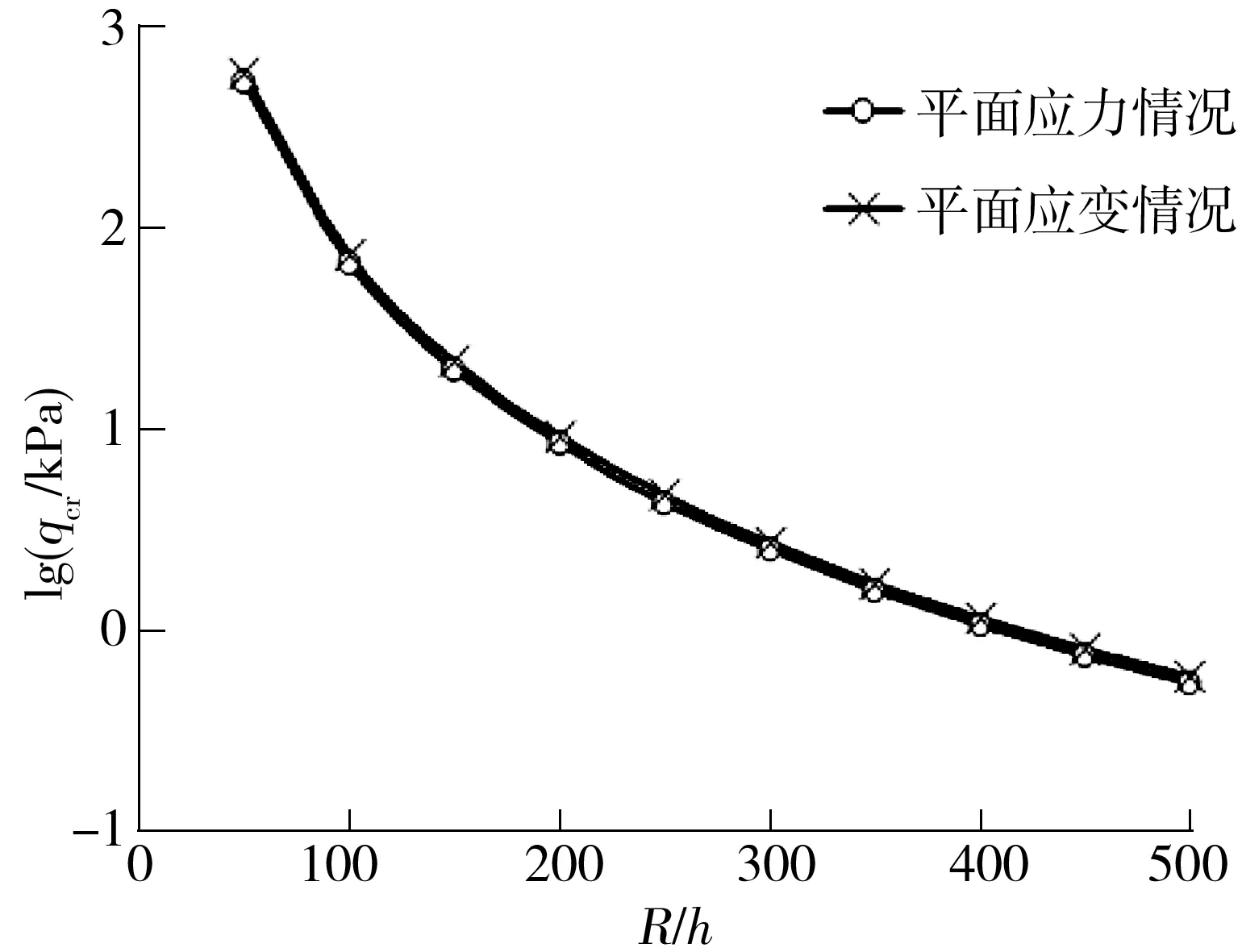
图2 不同径厚比FGM圆环的屈曲临界荷载曲线

Fig.2 Critical load curves of FGM rings with different radius-to-thickness ratios

选定径厚比R/h为100和200，材料组分参数k在0至100区间内变化.图3中，由FGM圆环的弹性屈曲临界荷载随组分参数k的变化可见，FGM圆环的弹性屈曲临界荷载随着组分参数的增大而单调递减，这说明，陶瓷含量较大的FGM圆环将具有较大的屈曲临界荷载.图3中显示，平面应变的结果略高于平面应力的结果.

图3 组分参数对FGM圆环屈曲临界荷载的影响

Fig.3 Effects of the inhomogeneous parameter on the buckling critical load of FGM rings

5 结论

文中针对静水压作用下平面应力和平面应变FGM圆环的弹性屈曲问题，推导得到了结构屈曲临界荷载的解析表达式，理论结果表明：平面应变状态下FGM圆环的屈曲临界荷载略高于平面应力的结果；随着径厚比的增大，FGM圆柱壳的屈曲临界荷载显著降低，而随着组分参数的增大，即FGMs中陶瓷组分含量的减小，屈曲临界荷载逐渐减小，在组分参数介于0.1至10的区间内下降较为明显.

[1] KOIZUMI M.The concept of FGM [J].Ceramic Transactions，1993，34(1):3- 10.

[2] TIMOSHENKO S P，GERE J M.Theory of elastic stability [M].London:McGraw-Hill，1963.

[3] FLAHERTY J E，KELLER J B，RUBINOW S I.Postbuckling behavior of elastic tubes and rings with opposite sides in contact [J].SIAM Journal on Applied Mathematics，1972，23(4):446- 455.

[4] HODGES D H.Non-linear inplane deformation and buckling of rings and high arches [J].International Journal of Non-Linear Mechanics，1999，34(4):723- 737.

[5] KIM Deokjoo，CHAUDHURI Reaz A.Effect of thickness on buckling of perfect cross-ply rings under external pressure [J].Composite Structures，2007,81(4):525- 532.

[6] 沈惠申.功能梯度复合材料板壳结构的弯曲、屈曲和振动 [J].力学进展，2004，34(1):53- 60. SHEN Hui-shen.Bending，buckling and vibration of functionally graded composite material plates and shells [J].Advances in Mechanics，2004，34(1):53- 60.

[7] SHEN Hui-shen，NODA N.Postbuckling of FGM cylindrical shells under combined axial and radial mechanical loads in thermal environments [J].International Journal of Solids and Structures，2005,42(16/17):4641- 4662.

[8] MATSUNAGA Hiroyuki.Thermal buckling of functionally graded plates according to a 2D higher-order deformation theory [J].Composite Structures，2009，90(1):76- 86.

[9] YAGHOOBI Hessameddin，FEREIDOON Abdolhossein.Mechanical and thermal buckling analysis of functionally graded plates resting on elastic foundations:An assessment of a simple refined nth-order shear deformation theo-ry [J].Composites Part B:Engineering，2014，62(1):54- 64.

[10] CHEN D，YANG J，KITIPORNCHAI S.Elastic buckling and static bending of shear deformable functionally graded porous beam [J].Composite Structures，2015，133(12):54- 61.

[11] MOHAMMAD B，REZA N，SHAHROKH H H.Buckling of FG circular/annular Mindlin nanoplates with an internal ring support using nonlocal elasticity [J].Applied Mathematical Modelling，2016，40(4):3185- 3210.

[12] KERDEGARBAKHSH M，KIANI Y，ESFAHANI S E，et al.Postbuckling of FGM rings [J].International Journal of Mechanical Sciences，2014，85(8):187- 195.

[13] LIEW K M，KITIPORNCHAI S，ZHANG X Z，et al.Analysis of thermal stress behaviour of functionally graded hollow circular cylinders [J].International Journal of Solids and Structures，2003，40(10):2355- 2380.

[14] 陈铁云，沈惠申.结构的屈曲 [M].上海:上海科学技术文献出版社，1993.

[15] GEORGE J Simitses，DEWEY H Hodges.Fundamentals of structural stability [M].Boston:Elsevier，2006.

Elastic Buckling of Functionally Graded Rings Under Hydrostatic Pressure

HUANGHuai-wei1ZHANGYong-qiang1,2HANQiang1

(1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, Guangdong,China; 2. Guangzhou Salvage Bureau, Guangzhou 510260, Guangdong, China)

In the buckling issue of pipelines, the structure is usually considered as a plane stress ring, but if there exists axial displacement constrain, the status may be closer to the status of a plane strain ring. In this paper, the elastic buckling problem of the plane-stress and plane-strain functionally graded material rings under hydrostatic pressure is theoretically investigated. It is assumed that the elastic material properties along the thickness direction continually changes according to the power law distribution. In this case, by combining the first shear deformation theory and the Kárman geometry relation and by employing the virtual displacement principle, a basic equilibrium equation of structures is deduced. Then, the buckling governing equation and the analytic solution to the structural buckling critical load are obtained by means of the eigenvalue method.Finally, the theoretical buckling perfor-mances of the structure in the plane-stress and plane-strain states are compared, and the influences of the structural radius-to-thickness ratio and the material constituent parameter on the performance are discussed. The results show that the buckling critical load of the plane-stain functionally graded material ring is slightly higher than that of the plane-stress case, and that as the inhomogeneous parameter of the material ranges from 0.1 to 10, the buckling criti-cal loads of the two kinds of rings decrease more obviously.

functionally graded materials;rings; buckling; virtual displacement principle

2016- 03- 22

国家自然科学基金资助项目(11402093)；机械结构强度与振动国家重点实验室开放课题项目(SV2016-KF-08)；华南理工大学中央高校基本科研业务费专项资金资助项目(2015ZZ130) Foundation item: Supported by the National Natural Science Edition of China(11402093)

黄怀纬(1979-)，男，博士，副教授，主要从事复合材料力学研究.E-mail:cthwhuang@scut.edu.cn

1000- 565X(2016)10- 0065- 05

O 343.9

10.3969/j.issn.1000-565X.2016.10.010