尺寸效应下的紫铜薄板力学性能试验研究*

张赛军 龚小龙 李健强 周驰 袁宁

(华南理工大学 机械与汽车工程学院∥广东省精密装备与制造技术重点实验室, 广东 广州 510640)

尺寸效应下的紫铜薄板力学性能试验研究*

张赛军 龚小龙 李健强 周驰 袁宁

(华南理工大学 机械与汽车工程学院∥广东省精密装备与制造技术重点实验室, 广东 广州 510640)

通过对0.1、0.2、0.4、0.6、0.8和1.0 mm厚的T2紫铜薄板在不同温度(450、650和850 ℃)下的热处理，获得不同的晶粒尺寸的试样，并采用数字图像相关性(DIC)方法对单向拉伸试验中的变形进行了测量，获得了相关力学性能参数(屈服强度、抗拉强度、最大均匀应变和断裂应变)与晶粒尺寸和板料厚度之间的关系.实验结果表明：所考察的退火T2紫铜薄板的力学性能参数均表现出明显的尺寸效应，抗拉强度、最大均匀应变和断裂应变均随材料厚度的减小或晶粒尺寸的增大而减小，且与厚度晶粒尺寸比呈近似指数关系.

尺寸效应；数字图像相关性；力学性能；T2紫铜

随着微型零件的广泛运用，对其成形过程的研究变得尤为重要，成形过程的力学性能和变形行为表现出对零件尺寸强烈的依赖性，这就是微成形中的尺寸效应.用传统的塑性理论已不能对微型零件的成形过程进行合理的描述，因此，对微成形中尺寸效应的理论研究具有十分重要的意义.

目前，针对尺寸效应对不同薄板材料的力学性能和变形行为的影响规律已有大量的研究.研究对象大体上分为厚度较大的薄板和厚度较小的箔板(厚度一般小于0.1 mm)，尺寸效应对这两类材料力学性能的影响展现出了不同的规律和特点[1].

对于薄板而言，尺寸效应对强度和变形的影响主要表现为“越小越弱”.Michel等[2]通过单向拉伸试验研究了CuZn36 薄板(厚度0.1～0.5 mm)的尺寸效应，试验结果表明，保持宽厚比不变，当坯料厚度由0.2 mm减小到0.1 mm时，流动应力减小；而在坯料厚度不变的情况下，试样的横截面积对材料的流动应力影响很小.Saotome等[3]采用基于图像传感器(CCD)测量的单向拉伸装置对板厚从 0.05 mm到 1.0 mm的不锈钢薄板进行了单轴拉伸试验，结果显示随着板厚的减小，抗拉强度和延伸率下降.Chan等[4]通过厚度为0.1～0.6 mm纯铜的单向拉伸试验，研究尺寸效应对断裂行为的影响，研究认为流动应力和断裂应力应变都随N值(试样厚度与晶粒尺寸之比)的下降而下降，其主要原因解释为：一是材料的晶界分数随N值的下降而下降，微孔洞随N值的下降而减少；一是在试样的侧面，由线切割造成的表面缺陷不随试样厚度的减小而减少，随试样厚度的减小，其影响变得越来越重要.王刚等[5- 6]通过微拉伸试验研究了0.05、0.1 和0.15 mm厚度的AZ31 镁合金轧制箔材的尺寸效应，试验结果表明在拉伸实验中，材料抗拉强度和延伸率都随着试样厚度的降低而降低.

对于箔板而言，由于材料很快发生断裂，延伸率都很小，因此研究主要集中在尺寸效应对强度的影响方面，主要表现为“越小越强”.Espinosa等[7]通过单向拉伸试验研究了不同厚度的铜薄膜的尺寸效应，实验结果表明：当薄膜的厚度由2.775 μm减小到0.265 μm时，屈服强度增大了将近3倍.张广平等[8]采用聚焦离子束在轧制的不锈钢薄膜上加工了不同厚度(约1.6～17 μm)的微悬臂梁试样，利用静态及动态弯曲加载研究了微米尺寸材料的形变与疲劳开裂行为，实验结果表明材料的屈服强度随薄膜厚度的减小而升高.Raulea等[9]采用三点弯曲的方法研究了Al 2S薄板尺寸效应，当N小于 1 时，N越小，屈服强度和抗拉强度反而越高.周健等[10- 12]通过基于CCD测量的单向拉伸试验研究了厚度为 20～100 μm 的轧制黄铜箔和厚度为20～320 μm 的轧制纯铜箔的尺寸效应，试验结果表明：在N接近4时，随着厚度的减小，屈服强度开始变化不大，当试样厚度继续减小至60 μm以下时，屈服强度反而快速上升.孟庆当等[13]通过单向拉伸试验研究了10～200 μm厚的SS304不锈钢薄板的尺寸效应，试验结果显示，对于不同厚度板料，屈服强度随板料的减薄而增加，并认为由于薄板的表层有一层韧性钝化膜，故会提高材料的屈服强度，随着板料厚度的减小，表面层所占比例越大，对屈服强度提升的作用就越大.

针对上述的尺寸效应现象，传统的材料模型已不再适用，因此建立微尺度下描述材料力与变形之间的本构关系尤为重要.Kals等[14]提出了表面层模型来解释材料流动应力随零件尺寸的减小而降低的现象.Peng等[15]基于表面层模型提出了一种混合本构模型，用来描述尺寸效应影响的材料的变形行为.近10年来，为解释材料在微米尺度下的尺寸效应现象，应变梯度理论发展尤为迅速，较为典型的有CS (偶应力)应变梯度塑性理论、SRG(拉伸与旋转)应变梯度塑性理论和MSG(基于机理)应变塑性理论[16- 20].Chan等[4]运用等应变模型和表面层模型描述了尺寸效应对纯铜变形行为的影响规律.

尽管目前对于尺寸效应的研究已经相当广泛而深入，但并没有合适的模型描述基本力学性能参数与尺寸效应之间的关系.文中主要结合数字图像相关性(DIC)方法，通过对退火T2紫铜薄板的单向拉伸试验，考察了尺寸参数(试样厚度、晶粒尺寸)对力学性能参数(屈服强度、抗拉强度、最大均匀应变和断裂应变)的影响规律.

1 试样制备与紫铜的拉伸试验

1.1 试验材料与试样制备

本研究以T2紫铜为研究对象，其厚度为0.1～1.0 mm，试样几何尺寸如图1所示.不同厚度初始坯料在真空条件下，通过450～850 ℃退火，并保温2 h，制成不同晶粒尺寸的试样.晶粒尺寸的测量依据“GB/T 6394—2002 金属平均晶粒度测定方法”，按比较法对各试样晶粒度进行评定，晶粒度评级完成后，参照标准评级系列图，获得晶粒的近似尺寸.不同厚度试样经不同退火温度后的晶粒尺寸如表1所示.图2和图3分别为初始材料和450 ℃热处理的不同厚度的紫铜金相图片.

图1 试样的几何尺寸(单位：mm)

退火温度/℃不同厚度紫铜薄板平均晶粒尺寸/mm0．1mm0．2mm0．4mm0．6mm0．8mm1．0mm4500．0530．0340．0340．0260．0670．0536500．1130．1500．1500．0450．0900．0908500．3000．3600．3600．3600．1500．440

图2 不同厚度初始紫铜材料的金相图片

图3 450 ℃退火后的不同厚度紫铜金相图片

1.2 T2紫铜的拉伸试验

不同厚度和不同晶粒尺寸的紫铜试样在常温下的单向拉伸试验在万能试验机上进行.需要注意的是，薄料(0.1和0.2 mm)的紫铜试样由于太薄，其

拉伸试验在岛津AG-500N拉伸机上进行；同时由于试样很快产生断裂，为了获得更多的试验数据，拉伸速度设为1 mm/min.厚料(0.4、0.6、0.8和1.0 mm)试样的单向拉伸试验在岛津AG-100KN拉伸机上进行，拉伸速度设为2 mm/min.拉伸机的采样周期为0.1 s.试验过程中材料的变形则通过Nikon D90单反相机进行记录，采样周期为2 s，并通过DIC方法计算全场应变.应变采用Ncorr软件进行计算[21]，主要参数为：子域半径、子域间隔和应变平滑半径分别设为21、1和5个像素.单向拉伸试验平台和不同热处理温度下不同厚度的紫铜薄板的工程应力-工程应变曲线分别如图4和图5所示.由图5可知，由于拉伸试样厚度和晶粒尺寸不同而导致的尺寸效应对退火T2紫铜的强度和变形都有很大的影响.

图4 试验平台组成

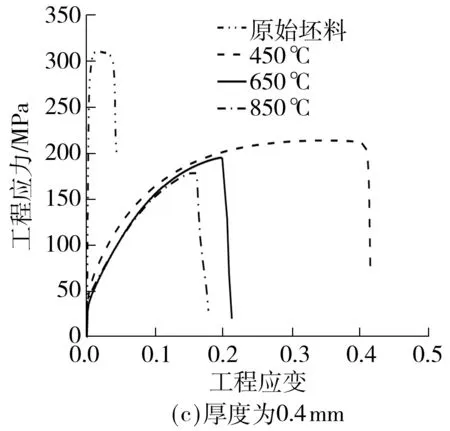
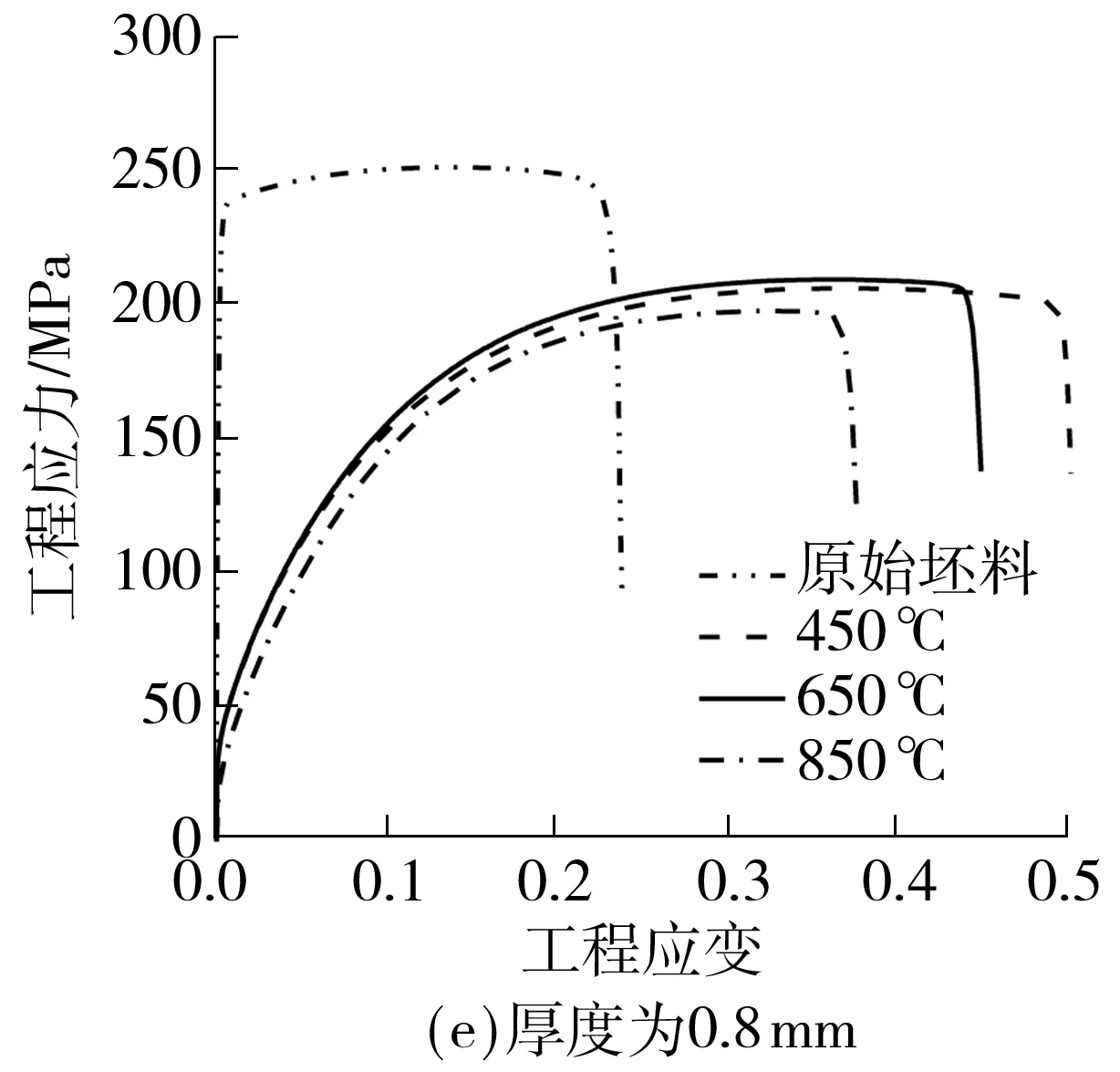
图5 T2紫铜试样工程应力-应变曲线

2 尺寸效应对T2紫铜强度的影响规律

不同厚度紫铜试样的屈服强度和抗拉强度与晶粒尺寸之间的关系分别如图6和图7所示.由图6可知，相同厚度材料的屈服强度总体上都呈现出随着晶粒尺寸的增大而减小的趋势；而当材料晶粒尺寸相同时，薄料和厚料表现出明显的强度差，薄料的屈服强度远高于厚料的屈服强度，且呈现出随着晶粒尺寸减小，强度差逐渐增大的趋势.晶粒尺寸从300 μm减小到50 μm时，薄料和厚料的平均屈服强度差从约30 MPa增大到约60 MPa，约增加了1倍.

由图7可知，与屈服强度的变化趋势类似，相同厚度材料的抗拉强度总体上也呈现出随着晶粒尺寸的增大而减小的趋势,体现出细晶强化的效果.材料厚度对T2紫铜的抗拉强度的影响则呈现典型的“越小越弱”的特点，即当材料晶粒尺寸相同时，抗拉强度随着材料厚度的减小而减小.不同厚度材料的抗拉强度存在明显的强度差，随着晶粒尺寸的减小，强度差逐渐减小.晶粒尺寸从300 μm减小到50 μm时，0.1 mm薄料和1.0 mm厚料的平均抗拉强度差从约78 MPa减小到约42 MPa，降幅约达到46%.

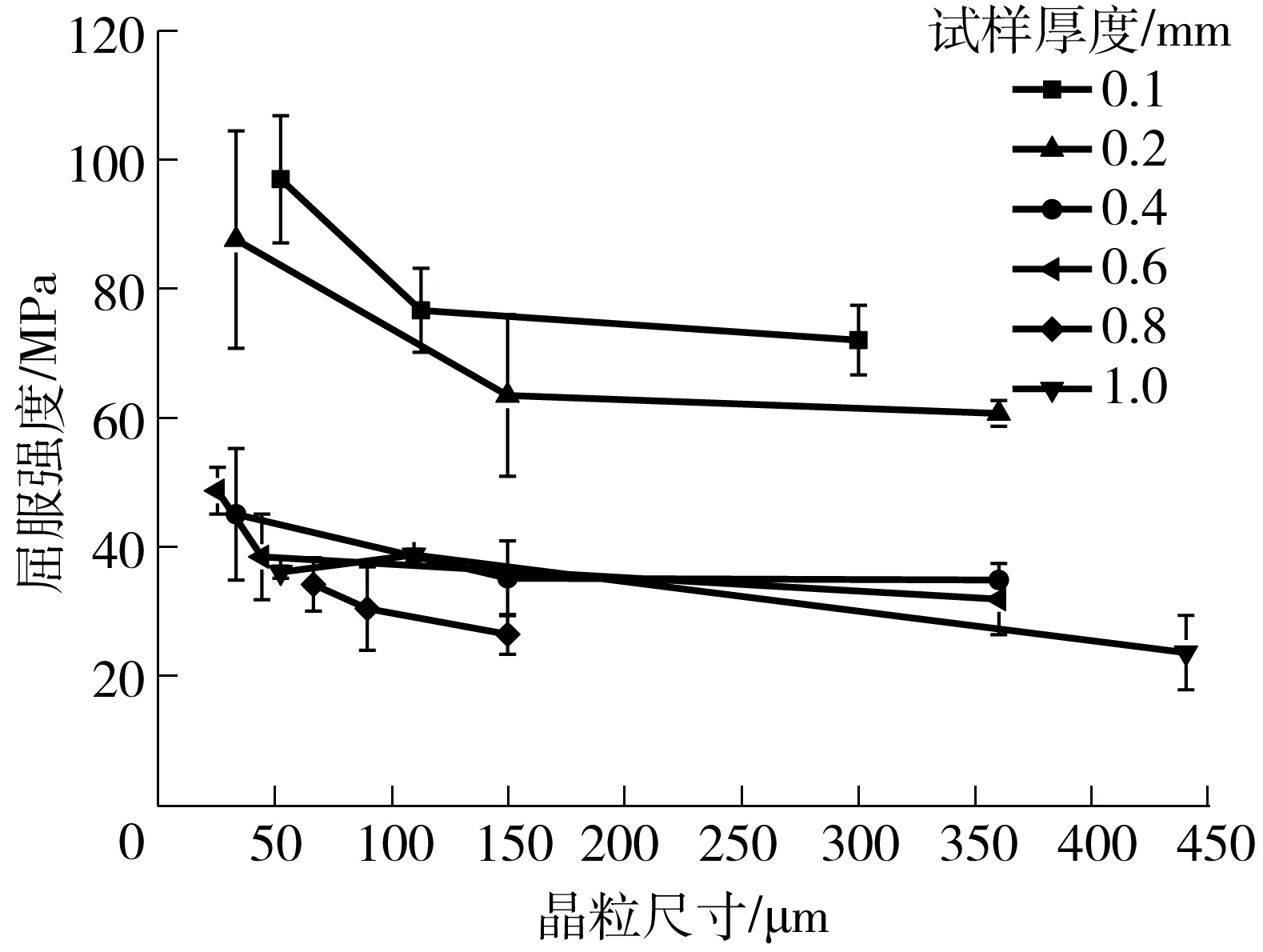
图6 T2紫铜屈服强度与晶粒尺寸的关系

Fig.6 Relationship between grain size and yield strength of T2 copper sheet

图7 T2紫铜抗拉强度与晶粒尺寸的关系

Fig.7 The relationship between grain size and tensile strength of T2 copper sheet

综上所述，材料厚度和晶粒尺寸都会对退火T2紫铜的屈服强度和抗拉强度产生很大的影响.为此，进一步考察了屈服强度和抗拉强度与厚度晶粒尺寸比N之间的关系，分别如图8和图9所示.由图8可知，在试样厚度不变的情况下，T2紫铜的屈服强度与N呈近似线性关系，屈服强度随着N的增大而增大.值得注意的是，薄料屈服强度与N之间的斜率明显要大于厚料，材料厚度对厚料的屈服强度与N之间的斜率的影响不大，薄料随着厚度的减小，其斜率逐渐增大，这与文献[12]对紫铜箔屈服强度的研究结果一致.

由图9可知，当N≤10时，抗拉强度与N之间的关系总体上呈指数关系，即尺寸效应对T2紫铜的抗拉强度的影响非常明显.当N>10时，抗拉强度并没有随着N的增大而发生明显的变化，这与常用的宏观材料几乎不考虑尺寸效应的常识相一致.根据这个特点，抗拉强度与N之间的关系可以用下面的公式很好地描述:

图8 屈服强度与N的关系

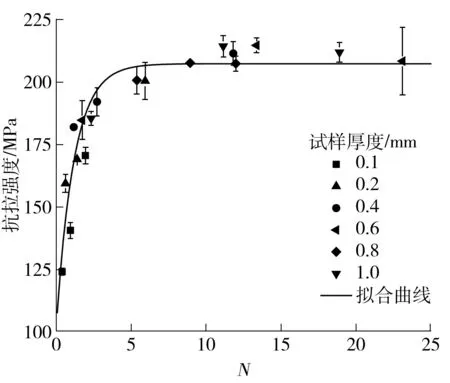
图9 抗拉强度与N的关系

σb=106.87+100.53×[1-exp(-0.84N)].

进一步考察可以发现，相同厚度下材料的抗拉强度与N之间呈近似线性关系，这和屈服强度与N之间的关系类似，即随着材料厚度的增加，抗拉强度与N之间的斜率逐渐变小，同时，材料厚度对薄料的抗拉强度与N之间的斜率的影响远大于厚料.

3 尺寸效应对T2紫铜变形的影响规律

尺寸效应除了影响材料的强度，还会影响材料的变形和断裂.由于DIC方法可以计算得到单向拉伸试验整个过程中的全场变形，因此可以考察尺寸效应与拉伸过程中的最大均匀应变、断裂应变之间的关系.最大均匀应变为抗拉强度处所对应的真实应变，断裂应变则取断裂前最后一幅图像上在局部颈缩区域的平均真实应变.

图10和图11分别为不同厚度的T2紫铜的最大均匀应变和断裂应变与晶粒尺寸的关系.由图可知，尺寸效应对最大均匀应变和断裂应变的影响规律基本一致.厚度相同时，T2紫铜的最大均匀应变和断裂应变均随着晶粒尺寸的增大而减小；0.1 mm厚的试样，当晶粒尺寸从50 μm增加到300 μm时，最大均匀应变和断裂应变分别从0.094和0.100下降为0.028和0.054，降幅均超过45%.1.0 mm厚的试样，当晶粒尺寸从53 μm增加到440 μm时，最大均匀应变和断裂应变分别从0.298和0.457下降为0.147和0.273，降幅均超过40%.

图10 紫铜薄板最大均匀应变与晶粒尺寸的关系

Fig.10 Relationship between largest uniform strain and grain size

图11 紫铜薄板断裂应变与晶粒尺寸关系

晶粒尺寸相同时，最大均匀应变和断裂应变均随着厚度的增大而增大.晶粒尺寸为50 μm左右，试样厚度从0.1 mm增大到1.0 mm时，最大均匀应变和断裂应变分别从0.094和0.100增大到0.298和0.457，增幅分别达到2.2和3.6倍.

最大均匀应变和断裂应变与N的关系分别如图12和图13所示.由图可知，最大均匀应变和断裂应变与N之间的关系和抗拉强度与N之间的关系类似，总体上也呈指数关系，当N>10时，最大均匀应变和断裂应变基本保持为常数，不再随着N的增大而发生明显的变化.拟合后的最大均匀应变和断裂应变与N的关系分别为

εM=0.030+0.282×[1-exp(-0.298N)]，

εf=0.038+0.456×[1-exp(-0.313N)].

综上所述，退火T2紫铜的抗拉强度、最大均匀应变和断裂应变与N之间的关系可以用下面的公式统一描述：

y=y0+ysat[1-exp(-n0N)].其中,y为抗拉强度、最大均匀应变或断裂应变，y0、ysat和n0为常数.由于N>0，该指数关系表明：随着N的变化，退火T2紫铜的抗拉强度、最大均匀应变和断裂应变在(y0,y0+ysat]之间变化.因此，y0和ysat分别表示相应的力学性能参数所能取得的最小值及其最大增量.n0则表示相应力学性能参数随着N的变化速率，n0越大意味着相应的参数随着N变大而增加越快，更容易达到饱和状态.需要注意的是，由于试验条件和试验数据点的限制，上述公式对于超薄材料(厚度小于0.1 mm)以及当N很小(N<1)时不一定适用，对其他材料的适用性也需要进一步考察.

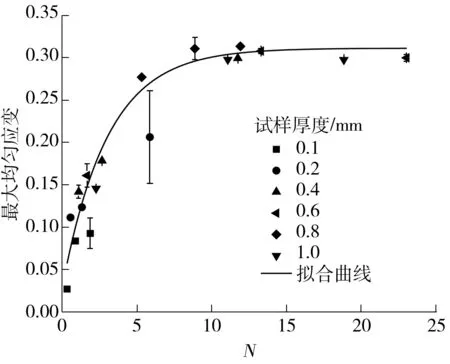
图12 紫铜最大均匀应变与N的关系

图13 紫铜薄板断裂应变与N的关系

4 结论

通过对不同厚度的T2紫铜薄板在3种不同温度下的热处理，获得不同的晶粒尺寸，并对0.1～1.0 mm之间6种厚度的紫铜薄板进行单向拉伸试验，获得了尺寸效应分别对屈服强度、抗拉强度、最大均匀应变和断裂应变的影响规律，主要获得了以下结论：

(1)相同厚度材料的屈服强度和抗拉强度体现为传统的细晶强化效果；而晶粒尺寸相同时，不同厚度材料的屈服强度和抗拉强度均表现出明显的强度差，且屈服强度差随着晶粒尺寸的减小而增大，而抗拉强度差则随着晶粒尺寸的减小而减小.

(2)尺寸效应对最大均匀应变和断裂应变的影响规律基本一致.厚度相同时，最大均匀应变和断裂应变均随着晶粒尺寸的增大而减小；晶粒尺寸相同时，最大均匀应变和断裂应变均随着厚度的增大而增大.

(3)抗拉强度、最大均匀应变和断裂应变与厚度晶粒尺寸比N总体上呈指数关系，可以通过公式很好地描述.当N≤10时，抗拉强度、最大均匀应变和断裂应变随着N的增加而快速增加；当N<10时均表现为饱和状态，即不再随着N的增大而变化.

[1] 单德彬,郭斌,周健.金属薄板微成形技术的研究进展 [J].塑性工程学报,2007,14(3):93- 99. SHAN De-bin,GUO Bin,ZHOU Jian.The research progress of micro sheet metal forming technology [J].Journal of Plasticity Engineering，2007,14(3):93- 99.

[2] MICHEL J F,PICART P.Size effects on the constitutive behaviour for brass in sheet metal forming [J].Journal of Materials Processing Technolgoy,2003,141(3):439- 446.

[3] SAOTOME Y,YASUDA K,KAGA H.Microdeep drawability of very thin sheet steels [J].Journal of Materials Processing Technology,2001,113:641- 647.

[4] CHAN W L,Fu M W.Experimental studies and numerical modeling of the specimen and grain size effects on the flow stress of sheet metal in microforming [J].Materials Science and Engineering,2011,528:7674- 7683.

[5] 王刚,张治朋,张建凯.镁合金板材正反向快速气压胀形实验 [J].塑性工程学报,2013,20(1):45- 47. WANG Gang,ZHANG Zhi-peng,ZHANG Jian-kai.The rapid pressure bulging experiment of magnesium alloy sheet [J].Journal of Plasticity Engineering,2013,20(1)：45- 47.

[6] WANG Gang,ZHANG Jiankai.Gas blow micro-bulging behavior for AZ31 magnesium alloy rolled foil [C]∥Proceedings of 5th Asian Workshop on Micro/Nano Forming Technology (AWMFT-2012).Harbin:Journal of the Japan Society for Technology of Plasticity：2012.

[7] ESPINOSA H D,PROROK B C,PENG B.Plasticity size effects in free-standing submicron polycrystalline FCC films subjected to pure tension [J].Journal of the Mechanics and Physics of Solids,2004,52:667- 689.

[8] 张广平,高岛和希,肥后矢吉.微米尺寸不锈钢的形变与疲劳行为的尺寸效应 [J].金属学报,2005,41(4):337- 341. ZHANG Guang-ping,KAZUKI Takashima,YAKICHI Higo.The size effects on deformation and fatigue beha-viors of micron-size stainless steel [J].Acta Metallurgica Sinica,2005,41(4):337- 341.

[9] RAULEA L V,GOIJAERTS A M,GOVAERT L E,et al.Size effects in the processing of thin metal sheets [J].Journal of Materials Processing Technology,2001,115(1):44- 48.

[10] 周健,郭斌,单德彬.铜箔抗拉强度及延伸率的尺寸效应研究 [J].材料科学与工艺,2010,18(4):445- 449. ZHOU Jian,GUO Bin,SHAN De- bin.The influence of size effects on tensile strength and elongation of copper sheet [J].Materials Science and Technology，2010,18(4):445- 449.

[11] 郭斌,周健,单德彬,等.黄铜箔拉伸屈服强度的尺寸效应 [J].金属学报,2008,44 (4):163- 166. GUO Bin,ZHOU Jian,SHAN De-bin,et al.The size effects on yield strength of yellow copper foil [J].Acta Metallurgica Sinica,2008,44 (4):163- 166.

[12] 周健,郭斌.铜箔力学性能的尺寸效应及微拉深成形研究 [D].哈尔滨：哈尔滨工业大学，2010.

[13] 孟庆当,李河宗,董湘怀,等.304 不锈钢薄板微塑性成形尺寸效应的研究 [J].中国机械工程,2013,24(2):280- 283. MENG Qing-dang,LI He-zong,DONG Xiang-huai,et al.The research of size effects on micro plastic forming of 304 stainless steel sheet [J].China Mechanical Engineering,2013,24(2):280- 283.

[14] KALS T A,ECKSTEIN R.Miniaturization in sheet metal forming [J].Journal of Materials Processing Technology,2000,103:95- 101.

[15] PENG L,LAI X,LEE H J,et al.Analysis of micro/mesoscale sheet forming process with uniform size depen-dent material constitutive model [J].Material Science Engineering,2009,526:93- 99.

[16] TAD MOR E B,PHILLIPS R,ORTIZ M.Mixed atomistic and continuum models of deformation in solids [J].Langmuir,1996,12:4529- 4534.

[17] EN S H,WANG T C.A new hardening law for strain gradient plasticity [J].Acta Materialia,2000,48:3997- 4005.

[18] CHEN S H,WANG T C.A new deformation theory for strain gradient effects [J].International Journal of Plasticity,2002,18(8):971- 995.

[19] CHEN S H,WANG T C.Strain gradient theory with couple stress for crystalline solids [J].European Journal of Mechanics A/Solids,2001,20:739- 756.

[20] 陈少华,王自强.应变梯度理论进展 [J].力学进展,2003,33(2):207- 216. CHEN Shao-hua,WANG Zi-qiang.The progress of strain gradient theory [J].Advances in Mechanics,2003,33(2):207- 216.

[21] BLABER J,ADAIR B,ANTONIOU A.Ncorr:open-source 2D digital image correlation Matlab software [J].Experimental Mechanics,2015,55(6):1105- 1122.

Experimental Investigation into Mechanical Properties of Copper Sheet with Size Effects

ZHANGSai-junGONGXiao-longLIJian-qiangZHOUChiYUANNing

(School of Mechanical and Automotive Engineering∥Guangdong Provincial Key Laboratory of Precision Equipment and Manufacturing Technology,South China University of Technology,Guangzhou 510640,Guangdong,China)

The tensile samples of different grain sizes were obtained by heating 0.1,0.2,0.4,0.6,0.8 and 1.0 mm T2 copper at 450,650 and 850 ℃.Then,the deformation of the samples in uniaxial tension tests was measured by the digital image correlation (DIC) method,and the relationships between the relevant parameters (namely,the yield strength,the tensile strength,the maximum uniform strain and the fracture strain) and the grain size as well as the sheet thickness are evaluated.Experimental results show that the mechanical properties of the annealed T2 copper sheet show an obvious size effect;specifically,the tensile strength,the maximum uniform strain and the fracture strain decrease with the decrease of the sheet thickness or the increase of the grain size,and they all have an approximate exponential relationship with the ratio of the sheet thickness to the grain size.

size effect;digital image correlation;mechanical properties;T2 copper sheet

2015- 12- 11

国家自然科学基金资助项目(51375172)；材料成形与模具技术国家重点实验室开放基金资助项目(P2014-02)；华南理工大学中央高校基本科研业务费专项资金资助项目(20152208) Foundation item: Supported by the National Natural Science Foundation of China(51375172)

张赛军(1978-)，男，副教授，主要从事先进材料成形工艺及理论研究.E-mail:mesjzhang@scut.edu.cn

1000- 565X(2016)10- 0008- 07

TH 142.3

10.3969/j.issn.1000-565X.2016.10.002