基于缸体腰形孔的柱塞腔抗空化结构的优化*

孙泽刚 肖世德 许明恒 魏巍

(1.西南交通大学 机械工程学院， 四川 成都 610031； 2.四川理工学院 机械工程学院， 四川 自贡 643000)

基于缸体腰形孔的柱塞腔抗空化结构的优化*

孙泽刚1,2肖世德1许明恒1魏巍1

(1.西南交通大学 机械工程学院， 四川 成都 610031； 2.四川理工学院 机械工程学院， 四川 自贡 643000)

为从结构上找到抑制液压元件空化的方法，从理论上分析了轴向柱塞泵缸体腰形孔结构对柱塞腔自吸力的影响，并通过Fluent软件对柱塞腔空化进行仿真分析.在Kriging插值原理基础上，建立了以缸体腰形孔结构参数为自变量及柱塞气体体积分数为目标函数值的代理模型，并通过杂交粒子群算法优化代理模型，得到缸体腰形孔优化结构，为解决柱塞泵结构参数的强耦合关系问题提供了新的方法.综合以上的分析，得到能最大限度抑制柱塞腔空化的柱塞泵缸体腰形孔及配流盘节流槽结构及其参数，通过仿真分析发现该结构具有很强的对柱塞腔空化的抑制性.

柱塞腔;空化;腰形孔；结构优化；杂交粒子群算法

在液压元件中，由于轴向柱塞泵具有额定工作压力高、效率高、极限功率大、变量调节方便等优点，常作为动力源广泛应用在农业及工程机械等液压系统中.近年来，许多学者开始关注水压轴向柱塞泵，并在该领域开展了研究工作[1- 2].与液压油相比，水具有饱和蒸汽压高、气体溶解度低的特点，因此水压轴向柱塞泵易发生空化[3- 4].

多年来，国内外学者对轴向柱塞泵空化进行了较为深入的研究，并取得了有价值的研究成果.Kosodo等[5]通过试验研究了液压系统中液压泵/马达配流盘V型节流槽的空化现象，发现V型节流槽中流度方向、温度、节流槽压差及雷诺系数对空化影响较大；Kollek等[6]通过空化过程中气泡发生、发展、溃灭时产生噪声的特性，建立了声音诊断信号与空化发生的关系，提供了空化初生的判断依据；Gold等[7]利用现代高速摄像技术，直观地观察玻璃管道内气泡的产生和发展规律，这种方法对轴向柱塞泵柱塞腔空化的研究有借鉴及指导意义；周华等[8]对海水液压泵的空化初生进行了实验研究，分析了空化初生的机理；刘晓红等[9]通过对配流盘节流槽结构对泵空化的仿真分析，指出节流槽流体流速大小、方向，以及节流槽两端压差均对其空化有影响，并通过改变配流盘节流槽结构，达到减小配流盘气蚀的目的；翟江[10]通过CFD对水压轴向柱塞泵内部空化流动进行了数值模拟，提出提高入口压力可有效减小柱塞腔空化；Xu等[11]通过模拟及试验手段分析比较了具有预升压和没有预升压轴向柱塞泵的流动波动，提出具有预升压轴向柱塞泵流动波动小，对柱塞泵的设计具有实际的意义；苑士华等[12]研究了轴向柱塞泵空化时气相动态演进过程，为柱塞泵空化研究提供了一种新的方法.

国内外学者对轴向柱塞泵气穴做了较多的研究，但考虑柱塞泵缸体腰形孔结构对柱塞腔空化的影响的研究鲜见报道.文中以长江液压元件有限公司某一型号的轴向柱塞泵为研究对象，以水为流体介质，通过动网格、滑移网格及UDF设置活塞的运动速度、流体可压缩性，建立泵工作过程中空化流动的CFD模型，分析缸体结构对柱塞腔空化的影响.

1 缸体腰形孔结构对柱塞腔自吸性能的影响

1.1 缸体腰形孔结构

缸体腰形孔结构如图1所示，其中δxy为缸体腰形孔轴线与XY面的夹角，δxz为缸体腰形孔轴线与XZ面夹角.根据角度值不同分为直腰形、单向倾斜式腰形、双向倾斜式腰性3种结构.表1为这3种缸体腰形孔的结构参数.

图1 缸体腰形孔结构

缸体腰形孔结构δxy/(°)δxz/(°)h/mm直腰形孔9007～15单向倾斜式腰形孔65～8507～15双向倾斜式腰形孔65～8510～147～15

1.2 倾斜式缸体腰形孔结构对柱塞腔自吸性能的影响

1.2.1δxy对柱塞腔自吸性能的影响

对于单向倾斜式腰形孔，由于缸体腰形孔相对于XY平面倾斜了一定角度δxy，如图1中A—A视图所示.当缸体高速转动时腰形孔中的流体会受离心力的作用(见图2)，有利于提高柱塞腔自吸能力.

流体在等直径管中流动时沿程压力损失如下：

(1)

缸体高速转动时，缸体腰形孔流体离心力沿缸体腰形孔轴线方向的分力为

(2)

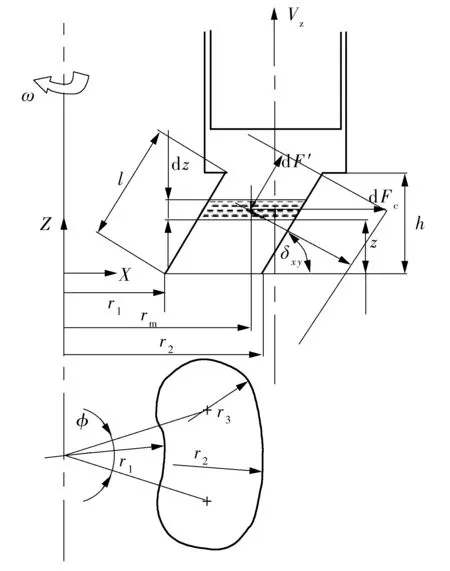
图2 单向倾斜式缸体腰形孔离心受力示意图

Fig.2Schematicdiagramofcentrifualforceofone-wayinclinedkidney-shapeholeofcylinderblock

δxy越小，缸体腰形孔流体的离心力越大，且沿缸体腰形孔轴线方向的分力F也越大，从而提高了柱塞腔的自吸能力，有利于抑制气穴.当δxy越小且缸体腰形孔管道厚度h越大时，缸体腰形孔管道长度l增加，从而加大了流体沿程压力损失，会减低柱塞腔流体的压力，促进气穴产生.因此柱塞腔空化程度与缸体腰形孔的δxy及h参数有关.

1.2.2δxz对柱塞腔的自吸性能分析

单向缸体腰形孔相对于X轴转动δxz后就形成了双向倾斜式缸体腰形孔.δxz对柱塞腔自吸能力的影响示意图见图3，图3为图1中B—B视图.

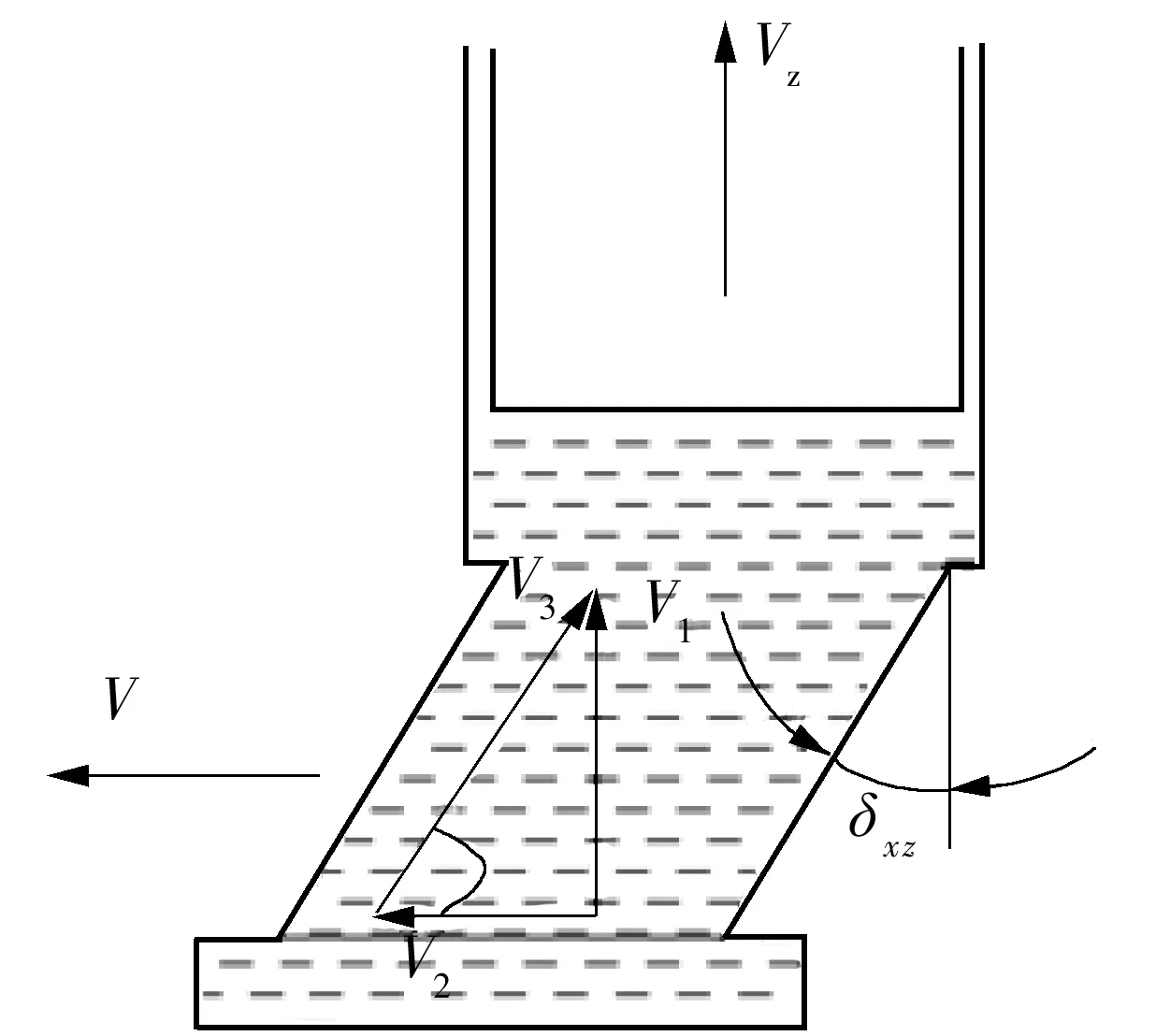
图3 δxz影响缸体腰形孔的流体流域分析

Fig.3 Analysis of the influence of the fluid drainage of the cylinder kidney-shape hole on theδxz

图3中V为缸体的线速度，缸体腰形孔流体切向速度V2=V，V1为流体进入缸体的腰形孔速度，则

(3)

从式(3)可知，θ1的大小与V1及缸体的角速度ω有关.V1的大小由柱塞腔柱塞运动速度Vz及柱塞泵入口压力p决定.当θ1与90°-δxz相近或相等时，可使缸体腰形孔内流体避免切向出现强涡旋现象，从而减小流动阻力.但因轴向柱塞泵在工作时柱塞的运动速度Vz是变化的，则缸体腰形槽中流体的轴向速度V1也是变化的，因此要使θ1与90°-δxz完全相等较困难.

2 倾斜式缸体腰形孔结构对柱塞腔空化影响的仿真分析

2.1 仿真对象

文中研究对象为水压轴向柱塞泵，斜盘倾角β为15°，交错角α取4°，柱塞个数为9，柱塞直径为21 mm，柱塞分布圆直径为81 mm，转速n为3 000 r/min.2.2 边界条件

(4)

式中，R为柱塞泵分布半径.

设定泵进口为压力进口、泵出口为压力出口，进出口处气体体积分数为零.采用商用Fluent软件，采用Mixture模型、RNGk-ε模型、动网格、滑移网格、通过UDF设定柱塞腔活塞运动速度及液态流体及气态流体的可压缩性.采用有限体积法和非交错网格对控制方程进行空间离散，湍动能项采用二阶迎风格式，其他各项采用一阶迎风格式，时间离散上采用二阶全隐式格式，动量方程中速度分量和压力耦合问题用SIMPLE算法.各迭代计算精度设置为10-8，时间步长设置为10-4.

2.3 缸体腰形孔厚度对柱塞腔空化的影响

仿真分析中缸体腰形孔的结构参数取值如下：h=7～15 mm，δxy=85°，δxz=0°，n=3 000 r/min.

不同h下柱塞腔气体体积分数(φ)变化曲线如图4所示.当h在7～11 mm之间时，随h值的增大时，φ的最大值变大，但当h值超过11 mm后，φ值随h值的增大而减小.这是因为当δxy较大时，只有当h值增加到一定时，才能使缸体腰形孔流体离心力沿缸体腰形孔轴线方向的分力克服缸体腰形孔沿程的压力损失.

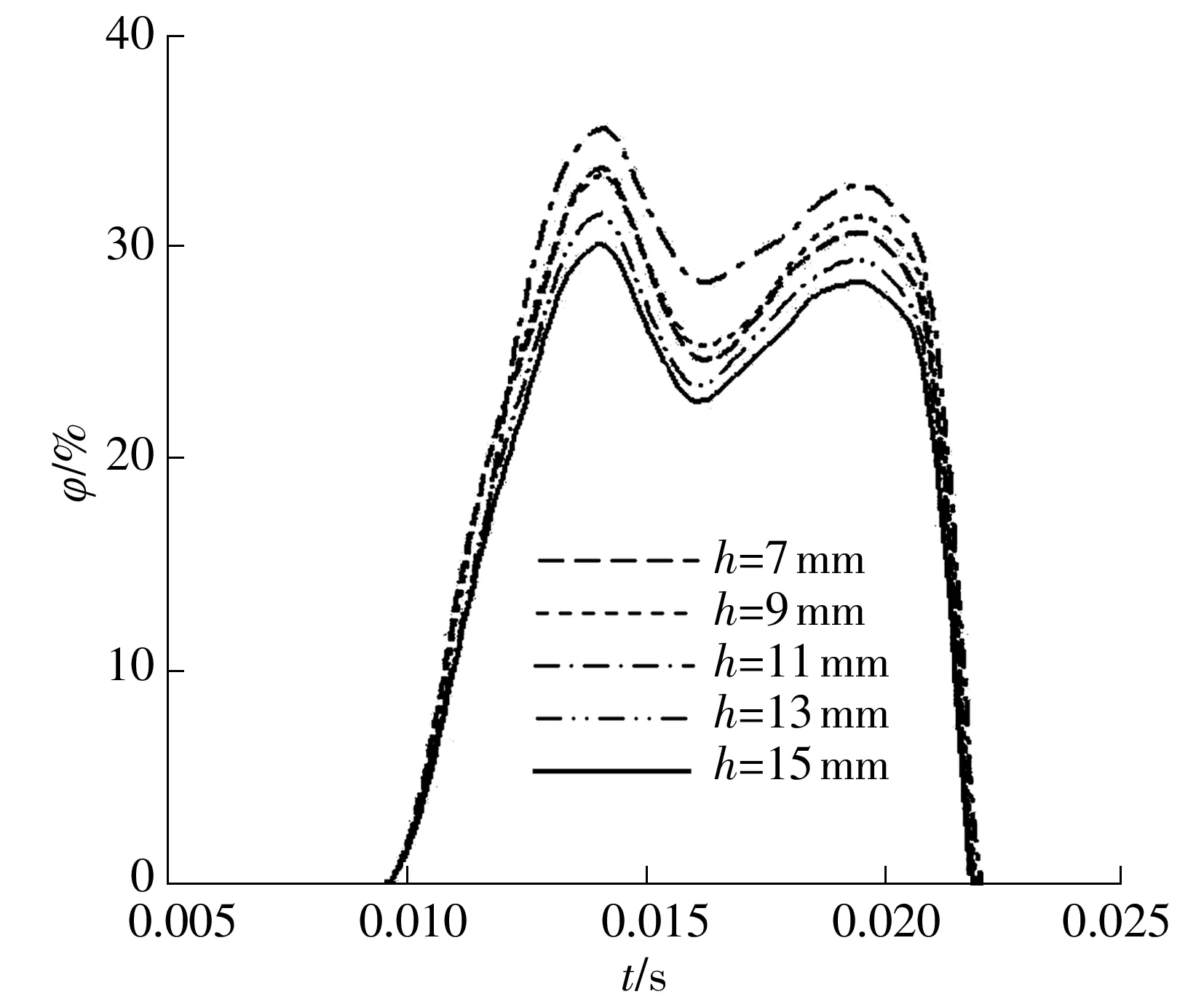
图4 不同缸体腰形孔厚度h下柱塞腔气体体积分数变化曲线

Fig.4 Change curves of gas volume fraction in plunger cavity under differenth

2.4δxy对柱塞腔空化的影响分析

仿真分析中缸体腰形孔的结构参数为：h=11 mm，δxy=65°～85°，δxz=0°，n=3 000 r/min.

不同δxy下φ的变化曲线如图5所示.从图中发现，δxy值越小时φ值就越小，说明缸体腰形孔流体在缸体高速转动时在离心力作用下加强了柱塞腔的自吸力，对柱塞腔的空化有一定的抑制性.

图5 不同δxy下柱塞腔气体体积分数变化曲线

Fig.5 Change curves of gas volume fraction in plunger cavity under differentδxy

2.5δxz对柱塞腔空化的影响

仿真分析中缸体腰形孔的结构参数为：h=13 mm，δxy=65°，δxz取值为0°、10°、12°、14°，n=3 000 r/min.不同δxz下φ的变化曲线如图6所示.从图中曲线的变化规律可发现，δxz对柱塞腔空化有明显的影响.

图6 不同δxz下柱塞腔气体体积分数变化曲线

Fig.6 Change curves of gas volume fraction in plunger cavity under differentδxz

0.010 s至0.014 s时间段是柱塞腔通过吸水口节流槽的时间区域.在这个时间区域内δxz值越大，此时的柱塞腔气体体积分数越大，这是由于随着δxz值增大，柱塞腔自吸力增大，流体过节流槽的速度增大.此时配流盘节流槽流体压力下降增多，空化严重，这主要是由节流槽的过流量增益小造成的.

0.014 s至0.020 s时间段柱塞腔已通过节流槽，此时间段柱塞腔气体体积分数先快速下降，然后又上升，这是由于柱塞的速度由慢变快造成的.在此区域中，δxz≠0°比δxz=0°对柱塞腔空化更有抑制性.δxz=10°时气体体积分数值在0.018 s后增加的梯度最小，同时气体体积分数值也最小.这主要是因为在δxz=0°时，θ1与90°-δxz匹配得最好，缸体腰形孔内流体减弱了切向强涡旋现象，减小了流动阻力.

3 单向倾斜腰形孔结构的优化

3.1 Kriging模型

Kriging模型是在已测定的样本点数据基础上，采用加权平均对相邻已知点之间区域内的未知量进行插值预测，并通过加权权值使预测值方差最小，是一种最优线性无偏估计[13- 15].孙泽刚等[16- 17]对节流槽结构进行了抗空化优化分析.

Kriging模型假设系统响应值与自变量之间的真实关系可以表示成如下关系式：

y(x)=f(x)Tβ+z(x)

(5)

式中，y(x)为未知点的函数估计，f(x)为已知关于x的函数(回归部分)，β为回归系数矩阵，f(x)Tβ是一个确定性部分.z(x)为随机分布的误差，是统计过程，其均值为0，方差不为0.

以Gauss函数为相关函数M，即

(6)

其中(θ,ζ,x)∈Rm,Rm为m维实向量.

3.2 Kriging代理模型的建立

综合前述，双向倾斜式腰形孔对柱塞腔空化有一定的抑制性.经过仿真分析发现，当δxz=10°时θ1与90°-δxz匹配得最好，此时柱塞腔空化程度最小.同时h及δxy同样影响柱塞腔的空化，但由于h及δxy具有一定的相关性，因此文中以Kriging插值原理为基础，以t=0.019 s时气体体积分数值为函数值，以h及δxy为自变量建立其Kriging代理模型.文中采用5水平全因子实验设计，h(单位：mm；下同)取值为{7,9,11,13,15}，δxy取值为{65°,70°,75°,80°,85°}，模拟分析了25个结构模型.回归模型为常回归模型，以Gauss函数为相关函数，建立Kriging代理模型，则φ值与h及δxy的近似曲面如图7所示.

从图7可以直观地观察出,当h在[14,15]及δxy在[70°,74°]区域时，φ最低.为提高代理模型精度，再以刚得到的Kriging代理模型为基础，以h取值为{14.2,14.4,14.6,14.8,15.0}、δxy取值为{70°,71°,72°,73°,74°}，得到25个代理模型估计值，重新得到h在[14,15]及δxy在[70°,74°]区域的Kriging小区域代理模型，其近似曲面如图8所示.

图7 Kriging代理模型近似曲面

图8 Kriging小区域代理模型近似曲面

3.3 杂交粒子群算法优化

采用杂交粒子群算法对Kriging小区域代理模型进行优化计算.设定粒子数目为40，学习因子1及学习因子2均为2，惯性权重为0.7，杂交概率为0.9，杂交池的大小比例为0.2，最大迭代次数为10 000，自变量个数为2.优化的结果为h=14.65 mm，δxy=70.34°，此时φ值为0.265 3.

3.4 柱塞泵缸体腰形孔优化结构的确立及仿真验证

根据杂交粒子群算法优化结果，确定单向倾斜式缸体腰形孔主要结构参数h=14.65 mm，δxy=70.34°，φ仿真分析结果如图9中的曲线1所示.

为进一步减小柱塞腔的空化程度，在已优化的单向倾斜式缸体腰形孔结构的前提下，综合2.5节

图9 优化结构柱塞腔气体体积分数变化曲线

Fig.9 Change curves of gas volume fraction in piston cavity of optimized structure

的分析，确定δxz=10°，仿真分析结果如图9中曲线2所示.

曲线2与曲线1进行比较，在0.016 s至0.020 s区间，柱塞腔的空化有一定的改善，但在0.010 s至0.014 s区间，柱塞腔空化却有增加.这主要是由于采用双向倾斜式缸体腰形孔后，增大了柱塞腔的自吸力，但由于配流盘的V形节流槽的通流量的增益不大，柱塞腔在通过V形节流槽时，发生了一定程度吸空.为改善这种情况，改配流盘的V形节流槽为L形节流槽，仿真分析结果如图9中的曲线3所示.根据图9中的3条曲线变化规律，很明显，与曲线3所对应的柱塞泵结构对柱塞腔空化具有明显的抑制性.

4 结论

通过文中对轴向柱塞泵的仿真分析及研究得出如下结论：

(1)δxy越小，缸体腰形孔流体的离心力越大，且沿缸体腰形孔轴线方向的分力F也越大，提高了柱塞腔的自吸能力，有利于抑制气穴.

(2)当θ1与90°-δxz相近或相等时，可使缸体腰形孔内流体避免切向出现强涡旋现象，从而减小流动阻力.但由于θ1是变化的，所以要达到θ1与90°-δxz完全匹配较困难.

(3)通过Kriging插值原理，建立了柱塞腔气体体积分数与单向缸体腰形孔结构参数的近似函数关系，解决了φ与柱塞泵结构参数的强耦合关系.通过分析得出最优双向倾斜式缸体腰形孔结构，其主要结构参数为h=14.65 mm，δxy=70.34°，δxz=10°，此结构对柱塞腔空化抑制性最好.

[1] NORMAN Bügener,HELDUSER S.Analysis of the suction performance of axial piston pumps by means of computational fluid dynamics(CFD) [C]∥Proceedings of the 7thInternational Fluid Power Conference.Aachen:National Fluid Power Association,Germany,2010:28- 33.

[2] MATTHIAS Heinz,RIDLEY Fidler,WERNER Dittrich,et al.Axial piston pump and motor optimization by means of CFD [C]∥Proceeding of the 7thInternational Fluid Power Conference.Aachen:National Fluid Power Association Germany,2010:53- 59.

[3] LIM G H,CHUA P S K,HE Y B.Modern water hydraulics-the new energy-transimission technology in fluid power [J].Applied Energy,2003,76(1/2/3):239- 246.

[4] YANG Huayong,ZHOU Hua.Some key problems of the water hydraulics [J].Chinese Journal of Mechanical Engineering,2002,38(Sup1):96- 100.

[5] KOSODO H,NARA M,KAKEHIDA S,et al.Experimental research about pressure-flow characteristics of V-notch [C]∥Proceedings of the Third JHPS International Symposium on Fluid Power.Yokohama:[s.n.],1996:73- 78.

[6] KOLLEK W,KUDZMA Z,STOSIAK M,et al. Possibilities of diagnosing cavitation in hydraulic systems [J].Archives of Civil and Mechanical Engineering,2007,7(1):61- 63.

[7] GOLD Sold,HELDUSER S,WUSMANN W.Experimental and numerical investigations of suction permanee of pumps [C]∥Proceedings of 6th International Fluid Power Conference.TU Dresden:National Fluid Power Association,2008:1- 2.

[8] 周华，杨华勇.海水液压泵气穴初生特征的识别 [J].机械工程学报，1999,35(6):52- 55. ZHOU Hua,YANG Hua-yong.Cavitation inception of sea water hydraulic pump [J].Chinese Journal of Mechanical Engineering,1999,35(6):52- 55.

[9] 刘晓红，于兰英，刘桓龙，等.液压轴向柱塞泵配流盘气蚀机理 [J].机械工程学报,2008，44(11):203- 208. LIU Xiao-hong,YU Lan-ying,LIU Huan-long,et al.Cavitation erosion mechanism of port plate of hydraulic axial planger pump [J].Chinese Journal of Mechanical Engineering，2008,44(11):203- 208.

[10] 翟江.海水淡化高压轴向柱塞泵的关键技术研究 [D].杭州：浙江大学，2012.

[11] XU Bing,SONG Yue-chao,YANG Hua-yong.Pre-compression volume on flow ripple reduction of a piston pump [J].Chinese Journal of Mechanical Engineering,2013,26(6):1259- 1266.

[12] 苑士华,周俊杰,罗先伟,等.轴向柱塞泵空化时气相动态演进过程及影响 [J].兵工学报，2015,36(3):559- 565. YUAN Shi-hua,ZHOU Jun-jie,LUO Xian-wei.Dynamic in evolution and effects of gas phase in cavitation of axial piston pump [J].Acta Armamentarii,2015,36(3):559- 565.

[13] 尹大伟,李本威,王永华,等.基于Kriging方法的航空发动机压力机特性元建模 [J].航空学报,2011,32(1):99- 106. YIN Da-wei,LI Ben-wei,WANG Yong-hua,et al.Aeroengine compressor characterictics metamodeling using Kriging method [J].Acta Aeronautica & Astronautiaca Sincica,2011,32(1):99- 106.

[14] SONG X G,WANG L,PARK Y,C.Analysis and optimization of butterfly valve disc [J].Journal of Process Mechanical Engineering,2009,223(2):81- 89.

[15] 谢素超,周辉.基于Kriging法的铁道车辆客室结构优化 [J].中南大学学报(自然科学版),2012,43(5):1190- 1198. XIE Su-chao,ZHOU Hui.Optimization on passenger compartment structure of railway vehicle based on Kriging method [J].Journal of Central South University(Science and Technology),2012,43(5):1190- 1198.

[16] 孙泽刚,肖世德,王德华,等.液压滑阀V型节流槽气穴仿真分析及结构优化研究 [J].兵工学报，2015,36(2):345- 354. SUN Ze-gang,XIAO Shi-de,WANG De-hua,et al.Cavitation flow simulation and structural optimization of hydraulic spool valve V-throttle groove [J].Acta Armamentarii,2015,36(2):345- 354.

[17] 孙泽刚,肖世德,王德华,等.多路阀双U型节流槽结构对气穴的影响及优化 [J].华中科技大学学报(自然科学版)，2015,43(4):38- 43. SUN Ze-gang,XIAO Shi-de,WANG De-hua,et al.Impaction and optimization of double U-throttle groove structure of multi-way valve on cavitation [J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2015,43(4):38- 43.

Optimization of Plunger Cavity Cavitation Based on Cylinder Block Kidney Shape Hole

SUNZe-gang1,2XIAOShi-de1XUMing-heng1WEIWei3

(1.School of Mechanical Engineering,Southwest Jiaotong University,Chendu 610031,Sichuan,China; 2.School of Mechanical Engineering,Sichuan University of Science and Engineering,Zigong 643000,Sichuan,China)

In order to find a way to restrain the cavitation of hydraulic components from the structure,the influence of the axial piston pump cylinder kidney shape hole structure on the self suction of the plunger cavity is theoretically analyzed,and the plunger cavity cavitation is simulated by using the Fluent software. Then,based on the principle of the Kriging interpolation,an agent model is constructed by taking the structure parameters of the cylinder kidney shape hole as the independent variable and the gas volume fraction of the plunger cavity as the objective function value. Moreover,the constructed agent model is optimized by using the cross breeding particle swarm algorithm,thus obtaining the optimized structure of the cylinder kidney shape hole,which provides a new method to overcome the strong coupling relationship between the structure parameters of the axial piston pump. According to the above analysis,the structure and parameters of the cylinder kidney shape hole and the valve plate groove of the axial piston pump,which can maximize the inhibition of the plunger cavity cavitation,are obtained. Simulation results demonstrate that the obtained structure can significantly inhibit the plunger cavity cavitation.

plunger cavity;cavitation;cylinder kidney shape hole;structure optimization;cross breeding particle swarm algorithm

2016- 01- 08

国家科技重大专项(2010ZX04015-011)；四川省科技计划项目(2015GZX0101) Foundation items: Support by the National Science and Technology Major Project of the Ministry of Science and Technology of China(2010ZX04015-011) and the Science and Technology Program of Scichuan Province(2015GZX0101)

孙泽刚(1975-)，男，博士生，副教授，主要从事机械电子及液压传动控制研究和流体CFD研究.E-mail:szg527@my.swjtu.edu.cn

1000- 565X(2016)10- 0036- 07

TH 137.51

10.3969/j.issn.1000-565X.2016.10.006