高等代数在数学分析极值问题中的应用

旷雨阳

(安顺学院数理学院，贵州 安顺561000)



高等代数在数学分析极值问题中的应用

旷雨阳

(安顺学院数理学院，贵州 安顺561000)

数学分析中的某些极值问题，如果使用数学分析中的方法解决，其过程可能相当繁琐，但若结合高等代数的方法，那么问题解决起来相当简单，文章以高等代数中的二次型与特征值探讨了多元函数的极值问题。

高等代数；数学分析；极值问题；简单应用

1、预备知识

定义1.2：设函数f(x,y)在点p(a,b)的领域G有定义，若∀(a+h,b+k)∈G，有f(a+h,b+k)≤f(a,b)(f(a+h,b+k)≥f(a,b))，则称p(a,b)是函数f(x,y)的极大点(极小点)，极大点(极小点)的函数值f(a,b)称为函数f(x,y)的极大值(极小值)。

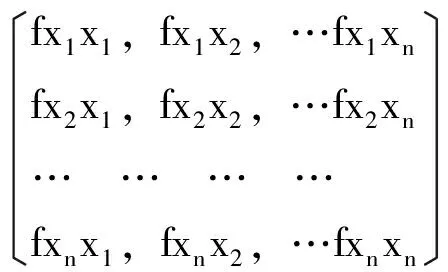
定理1.4：实对称矩阵A是正定的，当且仅当矩阵A的顺序主子式全大于零。

定理1.5：实对称矩阵A是负定的，当且仅当矩阵A的顺序主子式负正相间，

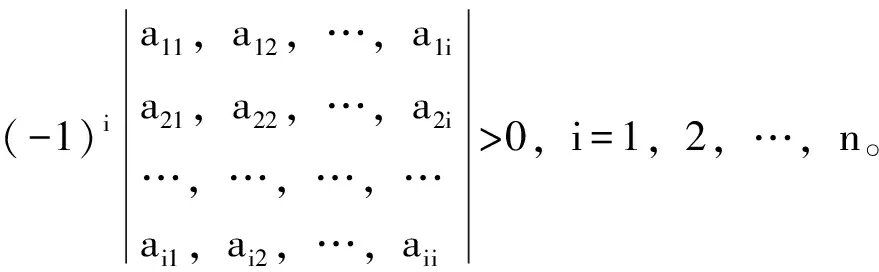
2、高等代数在数学分析极值问题中的应用

2.1 利用二次型求多元函数的极值

数学分析中有一些求多元函数的极值问题，利用高等代数的二次型来解决，可能会变得简单且通俗易懂。

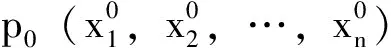
⑴当矩阵Hf(p0)是一个正定矩阵时，y=f(x1,x2,…,xn)在p0处取得极小值；

⑵当矩阵Hf(p0)是一个负定矩阵时，y=f(x1,x2,…,xn)在p0处取得极大值；

⑶当矩阵Hf(p0)是一个不定矩阵时，y=f(x1,x2,…,xn)在p0处没有极值。

证明：由f(x1,x2,…,xn)处在p0处的泰勒公式有：

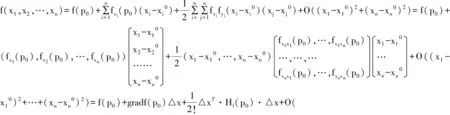
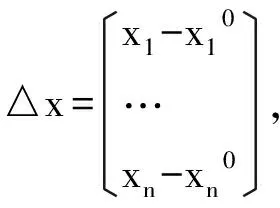
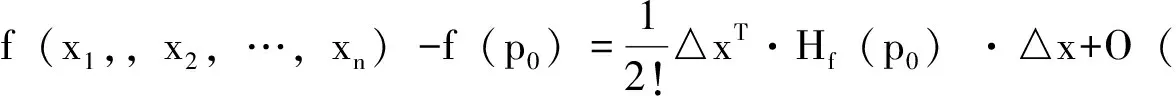
因此，如果矩阵Hf(p0)是正定矩阵时，二次型△xT·Hf(p0)·△x是正定二次型，即△xT·Hf(p0)·△x>0，于是在|△x|很小时，f(x1,x2,…,xn)-f(P0)>0，即y=f(x1,x2,…,xn)在点处取极小值。

同理，如果矩阵Hf(p0)是负定矩阵时，二次型△xT·Hf(p0》·△x是负定二次型，即△xT·Hf(p0》·△x<0，于是在|△x|很小时，f(x1,x2,…,xn)-f(p0)<0，即y=f(x1,x2,…,xn)在点p0处取极大值。

如果Hf(p0)是不定矩阵时，y=f(x1,x2,…,xn)在点P0处没有极值。

例3.1：求函数u=x3+3xy2-15x-12y的极值。

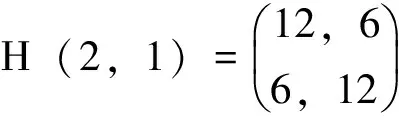
2.2 利用特征值求多元函数极值

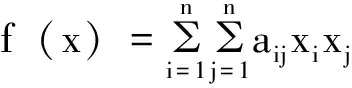
分析：本命题可以转化为高等代数中的二次型f(x1,x2,…,xn)=X′AX在X′X=1条件下的最大(小)值问题，然后利用特征值理论解决。

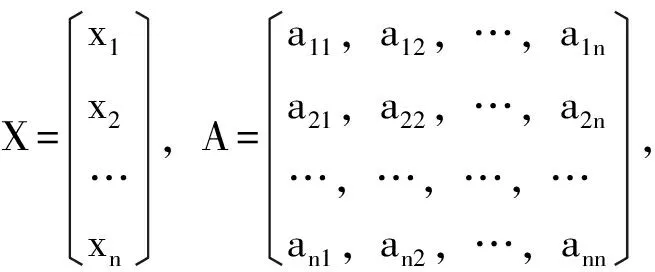
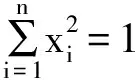
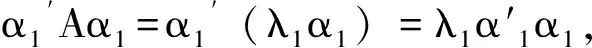
例2.2：设x,y是实数，且满足x2+xy+y2=3，求x2-xy+y2的最大值与最小值。

解：令则f(x,y)的矩阵令|λI-A|因此得特征值为由定理3.2得但注意到f(x,y)=3，解得2≤x2+y2≤6，又x2-xy+y2=2(x2+y2)-f(x,y)=2(x2+y2)-3，从而1≤x2-xy+y2≤9，故x2-xy+y2的最大值是9，最小值是1。

[1]旷雨阳· 谈谈数学分析与泛函分析的某些递进关系[J].科技通报. 2013(3): 20—22.

[2]严子谦，尹景学，张然· 数学分析中的方法与技巧[M].北京：高等教育出版社， 2009.

(责任编辑：王德红)

The Applications of Higher Algebra in Mathematical Analysis of Extreme Value Problem

Kuang Yuyang

(College of Mathematics and Physics，Anshun University，Anshun 56100,Guizhou,China)

Some extreme problems in mathematical analysis, If the method of mathematical analysis is used to solve the problem, the process may be very complicated, but the problem is solved fairly simply by combining the method of higher algebra. This paper is mainly to discuss the two times and characteristic value of higher algebra to solve the problem of the extreme value of multivariate function.

Advanced algebra，mathematical analysis，extreme value problem，simple application

2016-09-10

旷雨阳(1978.01～)，湖南攸县人，安顺学院数理学院副教授，硕士。研究方向：偏微分方程与最优控制。

O13

A

1673-9507(2016)06-0113-02

理工科教学与应用