数形结合 探索规律

查达彬

[摘 要]数形结合既是重要的数学思想，又是常用的数学方法。课堂教学中，教师如果长期渗透数形结合的思想方法，就能使学生形成良好的数学意识和解决问题的策略，长期稳固地作用于学生的数学学习过程中。

[关键词]画图 填表 数形结合 规律 方案 表达

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）35-017

我国著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微。”由此可见，数形结合在数学教学中的重要作用。

“打电话”这节课是人教版小学数学五年级下册综合应用中的一个内容，其中有这样一道题：“一个合唱队共有15人，暑假期间李老师接到一个紧急演出的通知，要合唱队的15名队员参加演出。如果以打电话的方式，每分钟通知一人，怎样尽快通知到每个队员？”下面，我就以“打电话”教学为例，谈谈如何运用数形结合，引导学生探索规律。

一、数形结合，尝试表达

教学片断1：

生1：我觉得一个一个地打电话通知浪费时间，分组通知应该快一些。

师：如果分组通知，你会怎么分组？通知完一共需要多长时间？（生小组讨论）

生2：我们小组把15人平均分成3组，每组5人，老师通知3个组长需要3分钟，组长再通知4个队员需要4分钟，一共需要7分钟。

生3：我们小组把15人平均分成5组，每组3人，老师通知5个组长，需要5分钟，组长再通知2个队员，需要2分钟，一共需要7分钟。

师：这两位同学不仅说出了平均分组通知所用的时间，还说出了平均分组通知的过程。不过，这个过程我们听起来还不够清晰，大家能否用简洁的图形把平均分组的过程表示出来？为了方便，我们不妨用“□”代表老师、用“○”代表组长、用“△”代表组员来画图，第几分钟就标上几。（学生画图后，师展示两位学生的作品，略）

师：这两位同学展示的图形清晰、美观，很好地表示出打电话通知的过程。

……

思考：对于五年级学生而言，平均分组通知的方案是比较容易找出来的。这里，在学生找出方案后，教师还让他们画图表达，不仅使学生进一步明晰平均分组通知的过程，而且引导学生尝试数形结合的方法，为后续应用数形结合的方法解决问题做好准备。

二、数形结合，优化方案

教学片断2：

师：同学们刚才已经会用图来表示平均分组通知的过程，这很不简单！但是，这两种方法是不是用时最短的方法呢？大家能不能通过画示意图找出用时最短或较短的方法呢？（生小组讨论并画图）

生4（出示下图）：我们小组通过画图觉得可以分成4组来通知，不过不是平均分组，而是有3个小组每组是4人，一个小组是3人，一共需要6分钟。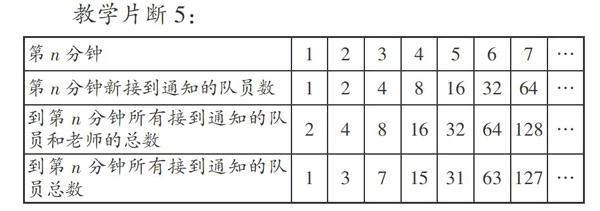

生5（出示右图）：我们小组通过画图认为可以分成3组来通知，不过也不是平均分组，而是分为6人、5人、4人三组，需要的时间也是6分钟。

生6（出示右图）：我们小组通过画图认为可以分成5组来通知，不过也不是平均分组，而是每组分别为5人、4人、3人、2人、1人，一共需要5分钟。

师：这三个小组同学探讨出来的方法，实际上就是不平均分组通知的方案。

……

思考：小学生年龄小，以形象思维为主，所以在学数学的过程中，往往会单维度的思考问题。课堂教学中，让学生画示意图，既可以把抽象的问题变得直观，又可以借助图形进行思维、想象，从而找出更省时间的方案。

教学片断3：

师：同学们真了不起，能够通过画图探究出这么多不平均分组通知的方法。但是，为什么不平均分组通知的方法比平均分组通知的方法花的时间都要少呢？

生7：我知道了！因为平均分组通知，老师、组长尽管都在帮忙通知，但由于组员数一样多，所以老师最后通知的那个组花的时间就要多一些，而不平均分组通知可以把老师先通知的小组多安排一些人，后通知的小组少安排一些人，这样就节省时间了。

师：这位同学说得真好！那么，用时5分钟是不是最短的时间呢？

生8：不是！因为画图时我发现用不平均分组通知的方法，尽管老师、组长都在通知，但不是始终都在通知，还有闲着的时候。我想，如果老师、组长和已接到通知的组员都全员参与通知，那还是可以节省时间的。

师：这位同学说得太好了！全员参与通知也就是大家都不闲着！那请大家继续通过画图，找出全员参与通知这种更省时间的方法。（生讨论并画图）

生9（出示下图）：全员参与通知只要4分钟。

生10（出示右图）：我画的图不一样，不过也只要4分钟。

师：同学们看一看，比较一下，哪位同学的画法更清晰？

生（齐）：最后一位同学的画法看得更清楚。

师：我们通过边画图边探究，想出了这么多好的方案。经过比较，大家觉得全员参与通知这种方案用时最少，只要4分钟，其原因是每个接到通知的队员包括老师在内都不闲着。

……

思考：在学生探究的过程中，数形结合为方案的不断优化起到了一个“拐杖”的作用，既促进学生积极思维，降低了学生探究的难度，又帮助学生发现并找到隐含其中的规律，让学生进一步体会到数学与生活的密切联系以及优化思想在生活中的应用。在此过程中，学生不仅品尝到了成功的喜悦，而且感受到数形结合这种方法的魅力。

三、数形结合，探究规律

教学片断4：

师：刚才我们研究的这个最省时的通知方案到底有什么规律呢？第1分钟通知了几人？

生11：第1分钟通知了1人。

师：接到通知的队员和老师的总数是几人？

生12：接到通知的队员和老师的总数是2人。

师：第2分钟呢？

生13：第2分钟通知了2人，接到通知的队员和老师的总数是4人。

师：第3分钟呢？

生14：第3分钟通知了4人，接到通知的队员和老师的总数是8人。

……

思考：探索最优方案中的规律是本节课教学的难点。学生在思考打电话的时间与通知到的队员人数的问题时，常会被表面现象所迷惑，而不能抓住事物的内在规律和本质——到第n分钟所有接到通知的队员和老师的总数是一个等比数列。上述教学，教师按时间顺序提问，通过不断深入，使学生对规律一步步明晰，为后面的填写表格埋下伏笔。

教学片断5：

师：通过填表，你发现了什么？（生小组讨论后汇报交流）

师生总结：后一分钟知道消息的人数是前一分钟知道消息人数的2倍，即知道消息的人数是成倍增加的，那么接到通知的总人数比知道消息的总人数少1人。

……

思考：上述教学，教师先出示表格，再让学生根据表格的内容要求计算填表，然后引导学生观察表格中的各项数据，分析各数据之间的关系并讨论交流。表格具有简单、明了、清晰的特点，通过表格的形式进行探究，有利于学生抓住事物的本质特点，总结出事物的变化规律，促进学生思维的发展。

四、数形结合，拓展延伸

教学片断6：

（1）快速抢答。

①李老师按每分钟通知1人计算，要通知31名舞蹈队队员，最少要几分钟？63人呢？

②按每分钟通知1人计算，第10分钟时共通知了多少人？

（2）小新是一名业务员。有一天，他帮老板谈成了一笔业务，让公司赚了500万元，老板很高兴，要奖励小新，让他提个要求。小新说：“我的要求不高，您只要从现在起第一个月给我1000元奖金，第二个月2000元，第三个月4000元，如此递增下去，连续奖我10个月就行了。”老板一听，要求不高，就答应了。你们知道第10个月要奖励小新多少元吗？（生答略）

师：回顾这节课的学习，你觉得最大的收获是什么？知道了哪些学习和研究方法？

……

思考：上述教学，通过拓展练习和这节课知识、学习方法的回顾，教师引导学生进一步梳理、提炼解决问题的方法和策略，使数形结合的思想方法深入学生心底，并内化为他们解决问题的习惯和技能。

总之，课堂教学中，教师如果长期渗透数形结合的思想方法，就能使学生形成良好的数学意识和解决问题的策略，长期稳固地作用于学生的数学学习过程中。

（责编 杜 华）