专业自主增设内容，回看陈题洞察结构——九年级“探究四点共圆”教学设计与解读

☉江苏省苏州工业园区青剑湖学校 王友峰

专业自主增设内容，回看陈题洞察结构
——九年级“探究四点共圆”教学设计与解读

☉江苏省苏州工业园区青剑湖学校 王友峰

在最近一次教学研讨活动中，笔者有机会执教九年级“探究四点共圆”，得到教师的好评.本文梳理该课教学设计，并解读设计意图，供研讨.

一、“探究‘四点共圆’”教学流程

教学环节（一）从三角形外接圆出发

图1

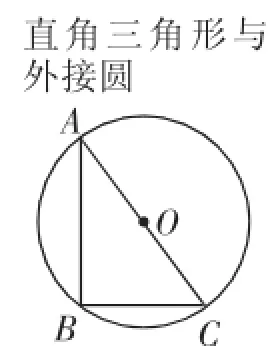
图2

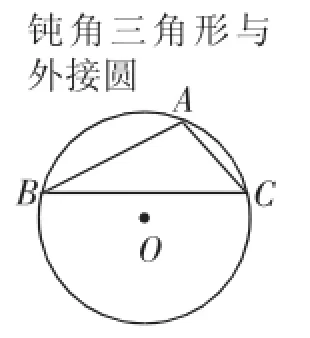
图3

提问：在⊙O上再取一个点D，观察、分析四边形ABCD有什么特殊.（圆的内接四边形对角互补）

预设活动：学生在上述图形中分别取一个点D，得出如下图形：

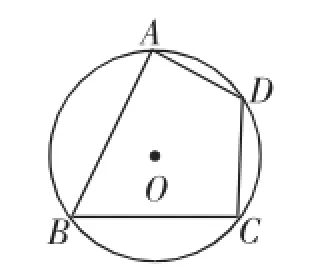
图4

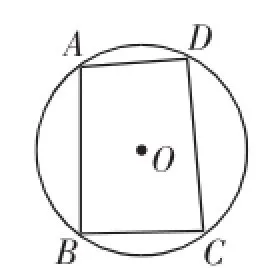
图5

图6

提问：这三个内接四边形中，哪一个可能成为平行四边形？为什么？

预设：图5中，该平行四边形此时应该为矩形.

教学环节（二）探究“四点共圆”

逆向思考：怎样的四边形能找出它的外接圆？

预设：比如矩形、等腰梯形、共斜边的两个直角三角形的四个顶点组成的四边形的共同特征，对角线并不一定相等，但对角互补.获得猜想：对角互补的四边形，过它的四个顶点能作一个圆.

预设：鼓励学生利用反证法证明命题“对角互补的四边形，过它的四个顶点能作一个圆.”

已知：如图7，四边形ABCD中，∠B+∠D＝180°.

求证：四边形ABCD内接于一个圆（A、B、C、D四点共圆）.

证明：用反证法，过A、B、C作⊙O，假设D不在⊙O上，则D在圆外或圆内.

若D在圆外，设CD交⊙O于D′，连接AD′，根据圆内接四边形的性质得∠B+∠CD′A＝180°.又∠B+∠D＝180°，则∠CD′A＝∠D.这与三角形外角性质矛盾，故D不可能在圆外.

类似地，可证D不可能在圆内.

则D在⊙O上，也即A、B、C、D四点共圆.

教学环节（三）例题训练，巩固新知

例1下列图形中，你发现哪四个点共圆？为什么？（1）如图8，PA、PB与⊙O分别相切于A、B两点.

图7

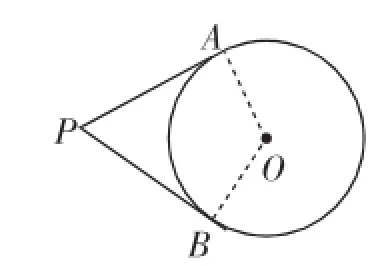
图8

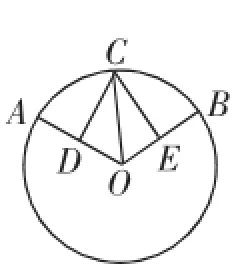
图9

图10

（2）如图9，⊙O中，点C是弧AB的中点，过点C分别作CD⊥OA，CE⊥OB，垂足分别为D、E.

（3）如图10，菱形ABCD的四边中点分别为E、F、G、H.

设计意图：通过四个学生熟悉的图形，引导他们发现其中的“四点共圆”.

例2圆在脑中：

（1）如图11，∠DCE是四边形ABCD的一个外角，如果∠DCE＝∠A，那么同时过点A、B、C、D能否作一个圆？

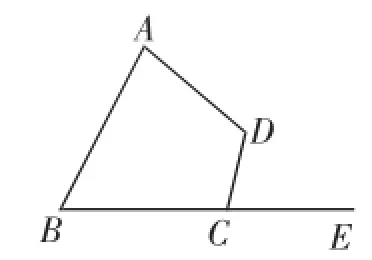
图11

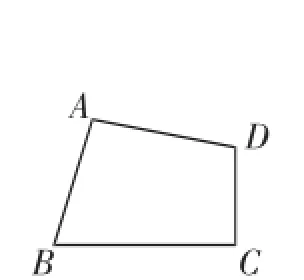
图12

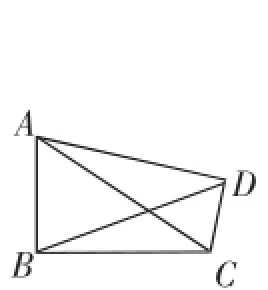
图13

设计意图：考查学生能否由四边形的对角互补判定该四边形的四个顶点共圆.

（2）如图12，经过四边形ABCD的四个顶点可以作一个圆，若∠A＝120°，则∠C的度数是？

设计意图：考查学生对圆内接四边形对角互补的掌握情况.

（3）如图13，在四边形ABCD中，∠ABC＝∠ADC＝90°，∠CAD＝16°，则∠ABD的度数是？

设计意图：考查学生对对角互补四边形四个顶点共圆的应用.

教学环节（四）反思“旧题”，看清“结构”

例3如图14，四边形ABCD是一个正方形.点E、F在边AD、CD上，且AE＝DF，连接BE、AF.

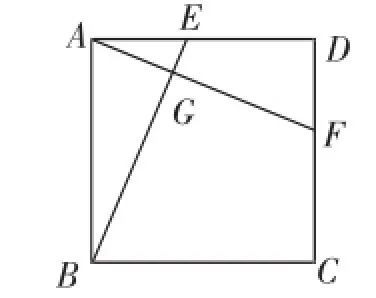
图14

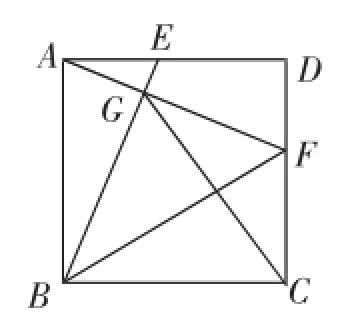
图15

（1）图中哪四个点在同一个圆上？为什么？

（2）如图15，连接CG、BF，求证：∠FBC＝∠FGC.

例4如图16，四边形ABCD是正方形，点E是BC的中点，∠AEF＝90°，EF交正方形外角的平分线CF于F.求证：AE＝EF.

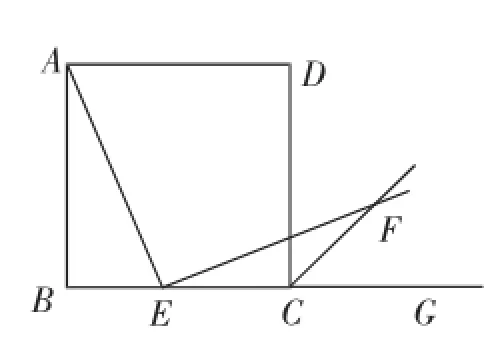
图16

图17

设计意图：学生如果基于全等的证法解决问题，则给出追问：有人发现基于构造圆的思考，点A、E、C、F四点在同一个圆上，也能解决这个问题，并引导学生发现图17这样的结构.

布置作业（略），下课.

二、教学立意的进一步解读

1.关注教材活动，专业自主组织“学材”

当前不少版本的数学教材在九年级圆这一章，都没有安排“四点共圆”作为一个课时来研究，然而我们在很多考题中见到“四点共圆”的结构.是在以后中考二次复习时再安排一节所谓的专题课复习四点共圆，还是在新授课结束之后的单元复习时就增设这一节习题课呢？我们选择了后者.因为九年级学生解题能力已经达到一定的高度，这里在单元复习时可以选择由三角形外接圆出发，自然而然地探究四点共圆，也是数学从特殊走向一般、成果扩大化的一种探究取向，是值得教学尝试的，更是我们一线教师专业自主的体现.想起著名特级教师李庾南老师近年来倡导的“学材再建构”，我们基于数学知识的前后理解，自主研发、组织教学内容，也应该属于一种积极的“学材再建构”吧.

2.预设开放问题，促进对话互动生成

在上述课例多个活动中，我们设计了多处开放式问题，比如，开课阶段安排学生作出不同三角形的外接圆，接着自主添加一个点D，研究四边形与外接圆问题；在探究新知环节，对于如何证明对角互补的四边形的四个顶点共圆，引导学生从反证法的角度思考问题，通过追问、对话，促进难点突破.在后续例题（例1、例2）题组的研究中，鼓励学生先猜想解答，再追问他们解答的依据，暴露思维过程.这样既使问题的呈现简约，又在对话、追问过程中追求了“开放的数学教学”（郑毓信教授语）.

3.回看经典习题，引导回顾反思结构

在例题教学的后半段，例3、例4分别选自八年级教材上的两道经典习题，在八年级，学生已经能利用四边形、全等三角形等实现证明，但证明的思路、步骤都较繁杂，而基于“四点共圆”的思路，则可以看清问题结构，获得更直接、深刻的证明与解答.这事实上也就是所谓的基于“高观点”下的解题追求.当我们站在区域性制高点俯看一些更初等问题时，往往能看得更全面和清晰.圆这一章作为平面几何图形最后的内容，自然有着很多统领性的功能和价值，这节课的学习，也是想让学生感受这种学习的深度与高度.

三、结束语

有了本次自主研发教学内容的尝试，我们更加感受到作为教师的专业自主的重要性，事实上就四点共圆的类似课例来说，仅在几何中就可研发很多类似的课例，比如八年级平行四边形一章中可以关注“中点四边形”“探究重心定理”，相似形中可探究“射影定理”等经典图形及性质.当然，我们的思考还是初步的，期待更多实践课例的分享与展示.

1.朱金祥.依赖“基本套路”，走向“用教材教”——李庾南老师“反比例函数”课例赏析［J］.中学数学（下），2016（10）.

2.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

3.陈爱军.预设互动促进对话，课件简约渐次展现——李庾南老师“函数的图像”课例赏析［J］.中学数学（下），2016（10）.

4.郑毓信.善于提问［J］.人民教育，2008（19）.Z