基于学情有的放矢，预设开放促进对话——“相似三角形的判定（2）”课例解读

☉江苏省沭阳县龙庙初级中学 王 静

基于学情有的放矢，预设开放促进对话
——“相似三角形的判定（2）”课例解读

☉江苏省沭阳县龙庙初级中学 王 静

初中几何的教学都是先学全等，隔了“较长时间”才学习相似，这时引导学生复习、类似全等学习相似很关键.笔者近期有机会开设相似三角形的判定（2）研究课，对“两角分别相等的两个三角形相似”一课的思考较为深入.本文梳理该课的教学过程，并跟进阐释教学立意，供分享与研讨.

一、“相似三角形的判定（2）”教学过程

教学环节（一）开课阶段，探究新知

问题1：我们已学习过哪些判定三角形相似的方法？（要求学生回顾、列举此前已学习的定义法、平行法、两边对应成比例且夹角相等、三边对应成比例）

问题2：类比全等三角形判定方法“ASA”，你能否猜想出新的相似三角形判定方法？

预设：如果有两角对应相等，则两个三角形相似.证明方法类似于此前两个定义的证明方法，这里让优秀学生口述证明思路即可.进而归纳出这种判定方法的文字表述和符号语言.

文字表述：两角分别相等的两个三角形相似.

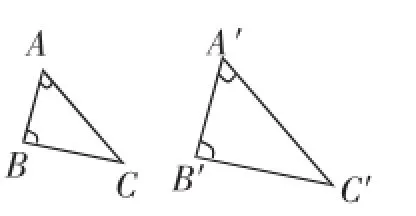
图1

符号语言：如图1，

∵∠A=∠A′，∠B=∠B′，

∴△ABC∽△A′B′C′.

教学环节（二）例题讲评，巩固新知

例1如图2，点D、E分别在AB、AC上，且∠ABC=∠AED.

（1）求证△ABC∽△AED；

（2）若DE=4，AE=5，BC=8，求AB的长.

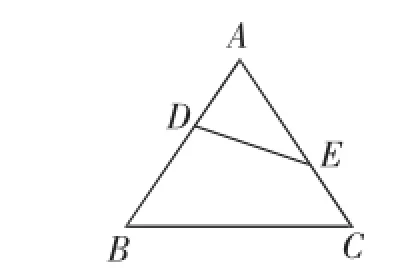
图2

图3

同类练习：如图3，已知在等腰三角形ABC中，顶角∠A=36°，BD为∠ABC的平分线，图中有相似三角形吗？

设计意图：例1及其同类练习主要训练新学的判定方法.同时同类练习也是一类经典图形：黄金三角形（顶角为36°的等腰三角形）.

例2如图4，在△ABC中，∠ACB=90°，CD⊥AB，垂足为点D.

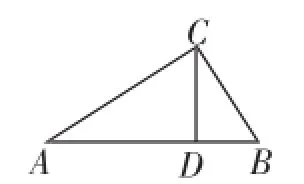
图4

（1）求证：CD2=AD·BD；

（2）你还能得出哪些“这样”的乘积式？

同类练习：在Rt△ABC和Rt△A′B′C′中，∠C=∠C′= 90°，若添加一个条件，使得Rt△ABC∽Rt△A′B′C′，则下列条件中不符合要求的是（）.

设计意图：例题及同类练习主要关注“射影定理”基本图形，这类图形有很广泛的应用，后续还会有丰富的变式与应用.

教学环节（三）综合拓展，引入圆的背景习题

例3如图5，已知△ABC和△ABD都是⊙O的内接三角形，AC和BD相交于点E.

图5

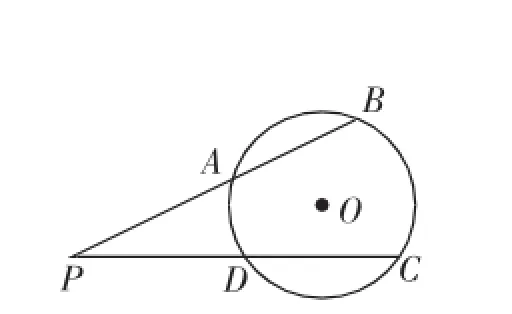
图6

（1）求证：△ADE∽△BCE；

（2）求证：AE·CE=BE·DE.

同类练习1：如图6，⊙O的半径为5，点P在⊙O外，PB交⊙O于A、B两点，PC交⊙O于C、D两点.

（1）求证：PA·PB=PD·PC；

同类练习2：如图7，⊙O是△ABC的外接圆，AB是直径，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E.（1）求证：△EBC∽△EAC；（2）若AE=6，CE=4，求⊙O的半径及阴影部分面积.

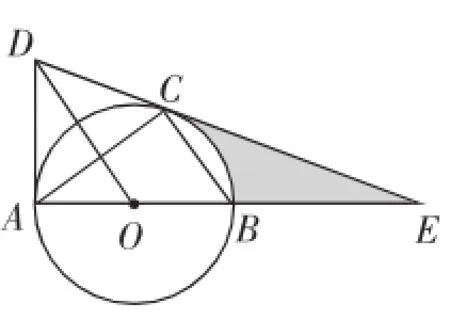
图7

设计意图：引入圆的背景问题，让学生在圆的背景问题中也能灵活地应用新知判定两个三角形相似，并解决相关问题.

教学环节（四）课堂小结，听课检测

问题1：通过本课的学习，有人说要判断两个直角三角形相似，只要找到一组角相等就可以.你觉得这个命题正确吗？

问题2：这节课中，你觉得哪一种图形值得积累？它能为你的解题带来哪些方便？

问题3：有人发现，过圆上任意一点作直径的垂线段，则垂足将直径分成的两条线段的积等于该垂线段的平方.你觉得他的发现正确吗？

听课检测：

题1：在Rt△ABC中，CD为斜边AB上的高.

（1）求证：AC2=AD·AB；

（2）若BD=1，AD=3，求BC、AC的长.

题2：如图5，已知△ABC和△ABD内接于圆O，AC和BD相交于点E.

（1）找出图中一对相似三角形，并证明；

（2）若AD=2，BC=4，BD=4，求DE的长；

（3）延长BA、CD交于点F，求证：FA·FB=FD·FC.

设计意图：这两道听课检测简单改编自上面的例2、例3，可有效检测学生听课的效果.而且图形及字母也没有变换，目的是让学生快速理解题意.

二、教学立意的进一步阐释

1.理解课标、理解教学，有的放矢组织教学内容

笔者备课时再次检索、研习《义务教育数学课程标准（2011年版）》，发现国家对相似三角形的判定的教学要求如下：

（4）了解相似三角形的判定定理：两角分别相等的两个三角形相似；两边成比例且夹角相等的两个三角形相似；三边成比例的两个三角形相似.*了解相似三角形判定定理的证明.

（5）了解相似三角形的性质定理：相似三角形对应线段的比等于相似比；面积比等于相似比的平方.

特别是，这里还增加了“底注：考试中，不要求用（4）（5）证明其他命题.”

根据以上表述，我们在预设本课教学时，没有纠结于如何引导学生证明相似三角形的判定定理，只是基于“上不封顶”的理念，让高层次学生“知其所以然”，安排优秀学生口述证明思路，使其知道这里的判定是“定理”而非“公理”.

2.基于学情增设内容，从“教教材”走向“用教材教”

由于证明“两角相等的三角形相似”定理的时间大大节省出来，故基于学情的理解，我们增加了例3，即以圆为背景的相似问题，而这些问题基于圆周角性质可以很快转化为新学知识的证明，使学生发现并证明“相交弦性质”，这样有利于学生获得一个整体观，也对不少练习题的快速求解带来帮助.

3.预设开放问题，促进教学对话、互动展示

南京大学哲学系郑毓信教授近年来一直倡导从开放题到开放的数学教学，并要求广大一线教师通过恰当的设问、追问，促进学生想得更深、更合理、更准确.基于上述思考，我们对不少例题的设问方式进行构思，比如例2在证出一个“比例中项”等式之后，追问“你还能得出哪些‘这样’的乘积式”，使得学生想得更深入、更全面，让不同的学生在同一个问题上有不同的收益和探究深度，并在后续交流展示过程中，让思考深刻的学生获得更多的学习成就感.

4.加强学情反馈，当堂开展听课检测

采用听课检测的方式，对本课讲评过的例题、习题进行简单改编，即时反馈教学效果，这种做法非常接地气，能弄清哪些学生是真懂、会做、做对.在本课的最后阶段，我们也安排了一组听课检测，分别改编自上面例题，图形与字母都没有改变，只是变换了问题的设问方式，有效检测了学生听课的效率.

三、写在最后

对常态课的教学设计研究是各级教研活动中比较薄弱的环节，本文选取平时教学进度中的一节常态课开展教学研讨，敬请同行批评指正，更欢迎类似的常态课的教学设计能呈现出来，以丰富常态课的教学研究.

1. 郑毓信.数学教师如何才能用好教材［J］.小学教学（数学版），2016（3）.

2.郑毓信.善于提问［J］.人民教育，2008（19）.

3. 中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

4. 郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.

5. 章建跃.构建逻辑连贯的学习过程使学生学会思考［J］.数学通报，2013，56（6）.Z