例说几何定理教学的层次——由傅种孙先生数学教育思想说起

☉江苏省苏州市苏州高新区第一中学 陈蓓蓓

例说几何定理教学的层次
——由傅种孙先生数学教育思想说起

☉江苏省苏州市苏州高新区第一中学 陈蓓蓓

近读《数学教育学报》，张英伯教授在《傅种孙——中国现代数学教育的先驱》（详见文1）一文中，回顾了傅种孙先生在数学教育上的贡献，比如：作为中国现代数学教育的先驱，傅种孙先生可谓呕心沥血，鞠躬尽瘁.他先后参与了教材的编写，课程标准的制订，致力于教师教育，并担任《数学通报》总编.特别是，傅先生在《平面几何教本》（见文2）的开篇就指出“知其然，知其所以然，何由以知其所以然，启发学者，示以思维之道耳！”也就是说，傅先生指出：“几何所追求的不是要知道它如此，而是要知道它为什么如此；不仅要知道它为什么如此，还得要领会从什么思路知道它所以如此.”受此启发，笔者结合近期教学实践，选取一些几何定理教学的片断例说数学概念教学的层次，提供研讨.

第一层次——知其然

由于这是最低的层次，几何中有大量的定理如果仅仅满足于让学生知晓、记熟，也会简单运算，则属于“知其然”的教学.

比如，勾股定理教学，有些初任教师没有在勾股定理的发现、证明上经营设计，而是采取避重就轻，简单告知勾股定理内容，学生记熟两直角边的平方和等于斜边的平方，然后进行大量的机械练习，巩固对勾股定理的记忆.这种低层次的勾股定理，将博大精深的数学知识简单化为一个孤立的知识点或公式教学，没有能发挥其应有的教育价值，只能是一种教学遗憾.

再比如，垂径定理的教学，如果仅仅从圆的轴对称性质归纳概括出垂径定理，而缺少对圆的轴对称性质进行追问和证明，则也只停留在知其然的层次.因为对“圆为什么是轴对称图形”的追问，会引导学生将这一逻辑链条下的轴对称图形的轴对称性质进行系统思考.我们注意到在文2中，江苏海安的陶然老师曾做过如下的教学设计（如图1～4）.

图1

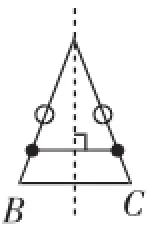
图2

图3

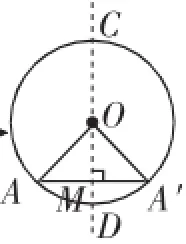
图4

教师引导学生退回最简单的线段，思考线段的轴对称性质如何证明，并一路生长到等腰三角形、矩形的轴对称性质，最后再让学生类比证明圆是轴对称图形，使得垂径定理的根基更牢固，定理的可信度更强.

第二层次——知其所以然

从第一层次而来，不仅知道具体的几何定理的内容与应用，而且要知道该定理如何证明？如何发现？到达知其所以然的层次是很多经验教师都能够达到的高度.在这个阶段，学生对数学新学概念的理解准确，是一种理解式的概念学习，而非记忆式的机械训练所得.

比如，初中阶段的三角形内角和定理的教学，不少教学设计是重复学生在小学阶段的操作实验，剪拼验证，然后再根据剪拼的操作示意，作出必要的辅助线实现证明则可看成是知其然，知其所以然.当然，我们也注意到有些老师对于三角形内角和定理的教学则更显数学味，他们往往引导学生思考三角形有哪些元素，三条边、三个内角，三条边之间的数量关系容易发现，而三个内角和为定值则可借助小学已有经验，然而小学并没有给出证明，初中阶段通过恰当的辅助线可以使得零散的三个内角集中到一起转化为一个平行，实现问题证明.综上，两种不同的处理都达到了证明三角形内角和定理的层次，而非停留在小学直观感知的初级阶段.

再比如，等边三角形的证明也是十分重要的.需要引导学生从不同的路径证明，感受殊途同归.如果从等腰三角形出发，强化出一个内角为60°后，又需要分两种可能，即该内角是顶角或底角，然后分别证明该等腰三角形三个内角都为60°，实现命题证明；另外，从一般三角形出发，如果找出两个内角为60°，则可结合三角形内角和证得三个内角均为60°，于是等边三角形获证.这里重要的不是具体的证明路径，而是证明起始阶段学生针对不同情况进行辨析，做好题设的识别，即找准出发点是证明等边三角形的关键.这样证明思路在后续学习矩形、菱形及正方形时道理是一致的.这也就是章建跃老师所倡导的要重视“基本套路”教学.

第三层次——何由以知其所以然

更高层次的几何定理教学则追求将不同的几何概念或定理、或推理都纳入一个有机会整体，让学生通过几何知识的学习感受到数学的整体一致、前后关系、逻辑连贯.

比如，圆周角定理的教学，首先引导学生观察猜想出同弧所对的圆内角是圆心角的一半，然后引导学生分类证明圆周角性质，最后综合起来得到圆周角定理：一条弧所对的圆周角等于它所对圆心角的一半.接着将图形特殊化，出现直径所对的圆周角为直角，而在这个推论中需要引导学生从“正、反”两个角度理解，首先是“正向思考”有直径所对的圆周角为直角；“逆向思考”有圆周角为90°时，所对的弦为直径，所对的弧为半圆.在此基础上还可将圆周角定理的基本图形拓展成圆内接四边形的问题，得出圆的内接四边形对角互补、圆的内接四边形的一个外角等于它的内对角.这些知识都可纳入到如下一个知识结构体系中，见图5（PPT截图）.

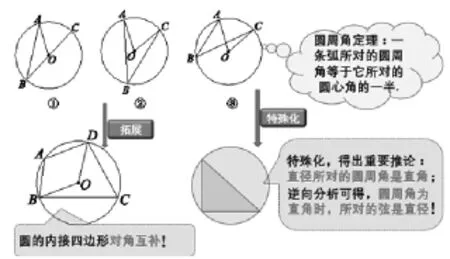
图5

类似地，我们上面提到的三角形内角和定理教学，也可以由三角形内角和出发，将三角形特殊化为直角三角形，则研究出两锐角的互余关系；将三角形特殊化为等腰三角形，可研究出顶角与底角之间的数量关系；将三角形的外角添出来，研究一个外角等于与它不相邻的两个内角的和，还可进一步得出三角形外角和为定值360°.它们之间的关系也可设计出PPT（如截图6）.

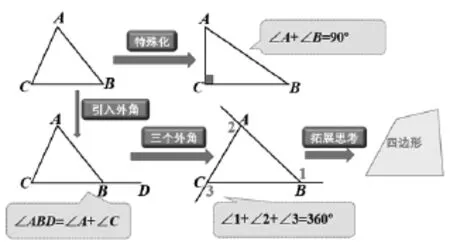
图6

行文至此，想起著名特级教师、江苏省南通市启秀中学李庾南老师在《自学·议论·引导教学论》中一篇课例，李老师没有“理会”《义务教育数学课程标准（2011年版）》中舍去平行线等分线段定理，而直接在相似三角形学习时给出所谓的平行线分线段成比例的“基本事实”，而是构造出下图（如图7）这样的教学设计路径：

图7

从图7中我们对平行线分线段成比例的源头、发展、特殊化都有清楚的表示，给学生带来的整体观、逻辑性、前后连贯性的启示作用是巨大的.我们常常羡慕专家教师的专业基本功，感动他们的教学定力，想来，对数学知识的精深独到的理解应该是专家教师们的特殊专业基本功吧.

1.张英伯.傅种孙——中国现代数学教育的先驱［J］.数学教育学报，2008（1）.

2.傅种孙.平面几何教本［M］.北京：北京师范大学出版社，1982.

3.陶然.优选“数学现实”，注重变式教学——以“垂径定理”教学为例［J］.中学数学（下），2015（10）.H