观摩“部优”课例，体会难点突破——勾股定理逆定理“部优”课例评析

☉江苏省南通市通州区兴仁中学 徐 芹

观摩“部优”课例，体会难点突破
——勾股定理逆定理“部优”课例评析

☉江苏省南通市通州区兴仁中学 徐 芹

教育部启动“一师一优课、一课一名师”活动以来，由于省、市、县各级教育行政部门的推进，很多老师加入晒课行列，从晒课平台上展示的“海量”课例来看，其中不乏优秀课例.本文关注一节勾股定理逆定理“部优”课例（见国家晒课平台，网址见文1），尝试评析该课的一些特点，供研讨.

一、“勾股定理逆定理”部优课例教学流程

教学环节（一）游戏引入

创设情境：给每组（两名）同学发30根木棒，请大家摆出直角三角形.

学生活动：借助三角板的直角，先拼出长分别为3和4的直角边，再拼上斜边5.

设计意图：设计拼图游戏，开课阶段调动学生的参与热情.并预设如下的PPT，截图如下（如图1～4）.

图1

图2

图3

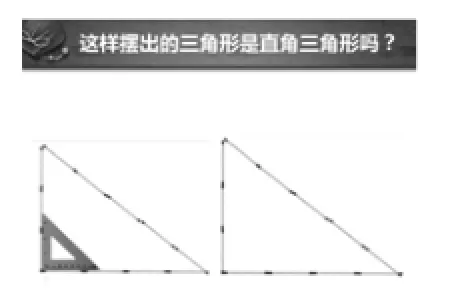
图4

教学环节（二）提出问题

问题：图2、图3中拼的图形都是直角三角形吗？

预设：以3和4为直角边的三角形，用勾股定理计算第三边长就是5.因此是直角三角形.用图3中的拼法拼得的三角形也是直角三角形吗？它和用图2中的拼法拼得的三角形是全等的吗？

追问：同学们认为三角形的三边满足什么样的关系就可以判定它们围成的三角形是直角三角形？

预设：安排学生证明勾股定理的逆定理，注意命题证明的格式，首先要根据题意画出图形，然后写已知和求证.

学生活动：用SSS证明两个三角形全等后明确逆定理：如果三角形的三边长a、b、c满足a2+b2=c2，那么这个三角形是直角三角形.

过渡：上述证明只是特例情形，如何推广到一般情形呢？

教学环节（三）形成新知

学生活动：利用已知条件作一个直角三角形，再证明其和原三角形全等，使问题得以解决.先作直角，再截取两直角边相等，利用勾股定理计算斜边A1B1=c，则通过三边对应相等的两个三角形全等可证.

设计意图：如何判断一个三角形是直角三角形？现在只知道有一个角是直角的三角形是直角三角形，从而将问题转化为如何判断一个角是直角.

教学环节（四）定理应用

例1由线段a、b、c组成的三角形是不是直角三角形？

a=3、b=4、c=6，a=1、c=3、b=3，a=9、b=12、c=15，a=12、b=16、c=20，a=30、b=40、c=50，a=300、b=400、c=500.

跟进猜想：在△ABC中，∠C=90°∠A、∠B、∠C的对边分别是a、b、c，请你判断以ka、kb、kc为三边的三角形是否是直角三角形.

设计意图：体会逆定理的条件实际上是三角形中较短的两边的平方和等于最长边的平方，巩固勾股定理逆定理及其应用

教学环节（五）实际应用

练习1：若小虫从A点出发，向正东爬行一段距离到达B点，然后向左拐前行至C点，如果你只有一把刻度尺，你能验证小虫现在前进的方向是正北方向吗？请说明理由.

追问：此时，如果你的刻度尺不够量出AC的距离，你能想出什么解决办法吗？

练习2：如图（图略），你能在单位正方形组成的网格图中标记的各点中选择两个点与C点连接而成一个直角三角形吗（不许用所有小正方形的直角）？你能找到几个满足要求的三角形？你是怎么找到的？它们之间是什么关系？

教学环节（六）小结作业（略）

二、课例评析

1.理解学情的前提下精准理解教学内容

在上这节课之前，学生已经掌握了勾股定理，可以直接应用勾股定理解决和证明问题，也具备一定的探究性学习和总结问题的能力.但对问题的总结及概括的准确度、完整度上还需要进一步训练.故设计经历勾股定理逆定理的探究及证明过程，并理解通过构造一个直角三角形，证明此三角形和原三角形全等，从而掌握证明三角形为直角三角形的方法.并且会应用勾股定理的逆定理判定一个三角形是否为一个直角三角形.这里的难点是勾股定理的逆定理的证明，特别是证明过程中从特殊走向一般的数学思想方法.以下再围绕难点突破展开详细评析.

2.勾股定理逆定理教学难点是如何突破的

从该课的开课引入开始，虽然是一个游戏情境，然而极具数学味，并没有让游戏味冲淡数学味，因为简短操作拼图之后，就是学生思考两种拼图为什么都能得到直角三角形，这是非常有挑战的数学问题.教师正是用这样匠心独运的活动设计，把勾股定理逆定理的证明精巧地包装、展示出来，接着安排学生证明特例情况下的勾股定理逆定理问题（如图5、6），由于学生在拼图过程中已有两种图形的经验，所以构造图6这样的辅助图形就容易想到，难点也就这样被突破了，教师的引导被巧妙地隐藏起来.有学者说教师要学会“匿身”，大概也是这个意思.接下来的另一个难点是，思考一般意义下的勾股定理逆定理的证明，其实就是将上述证明过程“一般化”，证明思路仍然是一致的.

图5

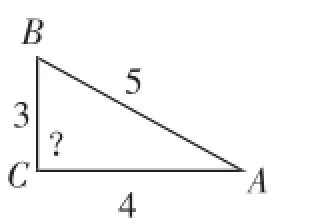
图6

3.注重从生活现实中恰当分离、抽象出数学问题

义务教育数学课程标准强调教学情境的创设要注意兼顾生活现实、数学现实和其他学科现实.从本课引入及课中素材的选择来看，教师注意选择了生活现实，且源于学生动手操作得到的数学问题，并通过恰当的追问使得生活问题“数学化”，抽象出数学问题，从而引入新知探究.这里既保证了学生动手操作的全员参与，又启发学生思维的参与，让更多学生的思维被“卷入”数学活动中.

4.晒课过程中的一些栏目规范值得关注

作为教育行政部门主导的大型晒课活动，分类查阅市优、省优、部优课例可以发现，这些获奖课例晒课的各个栏目都非常规范，比如教学目标、教学重点、难点分析，教学流程详实，设计意图解释清楚，配套的课件清新简约，随堂练习题设计恰当，上传的视频录制得也符合技巧规范.我们也注意到有些课例由于录制视频时晃动、音频也有噪声，使得观看效果不好；还有些课例视频录制得不错，但是配套展示的课件不太规范、各个栏目下的文本解读也不全，影响了评级的等次.

三、教学难点突破的进一步思考

我们知道，教学难点和重点有时并不是一回事，难点常常是高层次学生能够接受和挑战的数学知识，而难点如何突破又影响着这部分学生更顺畅地理解教学难点.像本文课例中这节“部优”课例，对教学难点的认识是准确的，教学难点的突破是艺术的，润物无声值得学习.以下再围绕教学难点的突破给出两点思考.

1.对教学难点的认识要认真读教师用书

教师用书是教材编写组对教材的进一步解读，写给教师看的，往往对教学重点的揭示、教学难点的辨别都写在教师用书的边栏、底栏，如果教师在备课时不注意阅读教师用书，而根据主观判断，则有时容易混淆教学难点和重点.

2.教学难点的确定还要兼顾学情实际

教学难点除了兼顾教师用书上教材编写者的提示，还需要基于我们的实践经验，针对所教学生的学情进行取舍.如果整体学情薄弱，则有可能教学难点需要适当放弃或进一步铺垫才能顺利攻克教学难点.比如，七年级有理数乘法的“负负得正”这一教学难点的突破，甚至教材也采取了模糊的处理，而不再纠结于如何说清“负负得正”的证明，因为不管我们如何努力，试图明辨其中道理，效果往往适得其反，这时还不如以一组算式的运算，归纳猜想出“负负得正”的法则.

1.http：//1s1k.eduyun.cn/portal/1s1k/sportal/index.jsp？sdResIdCaseId=ff8080814cf994a3014d03b9944a6c5b&t= show.

2.刘东升.基于HPM视角重构“勾股定理”起始课教学［J］.教育研究与评论（课堂观察版），2016（1）.

3.蔡宗熹.千古第一定理——勾股定理［M］.北京：高等教育出版社，2013.Z