从“标准”到“变式”，从封闭走向开放——以“全等三角形”起始课教学为例

☉江苏省南通市北城中学 顾为秀

从“标准”到“变式”，从封闭走向开放
——以“全等三角形”起始课教学为例

☉江苏省南通市北城中学 顾为秀

最近一次学校教研活动中，笔者有机会执教“全等三角形”研究课.本文整理该课的教学设计，并阐释设计意图、跟进教学反思，供研讨.

一、“全等三角形”教学设计

教学环节（一）折纸活动，引入新课

折纸操作：学生将纸对折，在一面上画出一个三角形，并用剪刀剪下这个三角形（两张纸一起剪），同时得到两个三角形.观察：这两个三角形的形状、大小有何关系？

问题1：观察下列图案，指出这些图案中形状与大小相同的图形.

图1

问题2：从上面的片段中你有什么感受？还能举出生活中一些这样的例子吗？收集学生讨论中的图片，接着追问：上面这些图形有什么共同的特征呢？

问题3：把三角形平移、翻折、旋转后，什么发生了变化，什么没有变？

设计意图：丰富的图形容易引起学生的注意，使他们很快投入学习的情境中去.通过观察发现其中的共同特点，形成猜想；通过构图和操作，为学生理解全等三角形的有关概念奠定基础.

预设：安排两个学生在黑板上演示并画图，其他学生在练习本上操作.教师利用课件动画演示旋转前后的两个三角形，位置变化了，但形状、大小都没有变，它们依然全等.

讲解：这些形状、大小相同的图形放在一起能够完全重合.能够完全重合的两个图形叫作全等形.能够完全重合的两个三角形叫作全等三角形.“全等”用≌表示，读作“全等于”.

两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上，如图2，△ABC与△DEF全等时，点A和点D，点B和点E，点C和点F是对应顶点，记作△ABC≌△DEF.

图2

把两个全等的三角形重合到一起，重合的顶点叫作对应顶点，重合的边叫作对应边，重合的角叫作对应角.

即时训练：（找出全等三角形中的对应元素）以下面的图形为例（如图3、图4、图5），由学生先独立识别对应元素，然后集体交流.

图3

图4

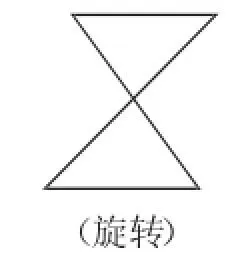
图5

问题4：你能“构造一对全等三角形”吗？在同组内交流你是如何构造的.

问题5：全等三角形的对应边、对应角有什么数量关系？为什么？

预设：学生依据课本内容和自己的思考容易答出：全等三角形的对应边相等、对应角相等.请写出平移、翻折后两个全等三角形相等的角、相等的边.

设计意图：利用三角形的平移、旋转、翻折的不变性，让学生通过具体操作直观感知全等三角形的概念，然后让学生通过操作和观察，猜测并验证三角形的性质，这种效果是抽象的讲授难以达到的，利用基本三角形变化变形出各种图形，然后观察它们的对应边、对应角的变化，有利于提高学生识别图形的能力.

教学环节（二）典例训练，建立模型

例1已知：如图6，△ABC≌△DEF.

（1）若DF=10cm，则AC的长为_____；

（2）若∠A=100°，则∠D的度数为_____；

（3）若∠A=100°，∠B=30°，求∠F的度数.

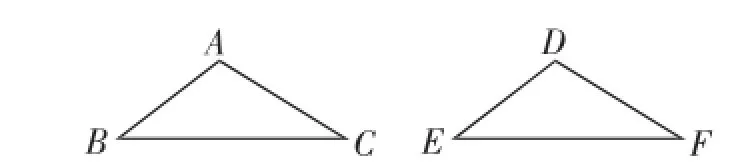
图6

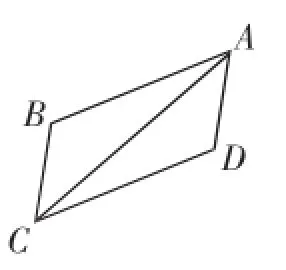
图7

例2如图7，△ABC≌△CDA，AB与CD、BC与DA是对应边，则下列结论错误的是（）.

A.∠BAC=∠DCAB.AB∥DC

C.∠BCA=∠DCAD.BC∥DA

设计意图：两个例题都是全等三角形的初级题目找对应元素，其实不是一件容易的事情，特别是从一个较复杂的图形中快速确定对应元素，比如可利用PPT呈现下面的系列图形（图8），按下列图形的位置摆放，指出它们的对应顶点、对应边、对应角.

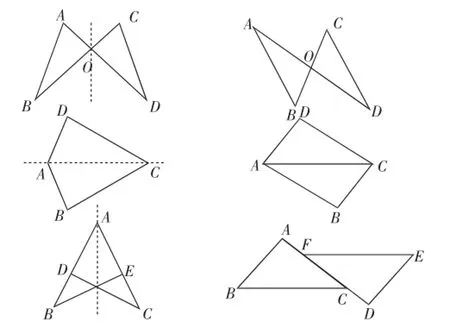
图8

即时训练：如图9，△ABE≌△ACD，AB与AC、AD与AE是对应边，∠A=40°，∠B=30°，求∠ADC的大小.

图9

追问1：从刚才的练习中，你认为全等三角形对应顶点、对应边、对应角之间有什么关联呢？

预设：全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边；对应边所对的角是对应角，两条对应边所夹的角是对应角.

追问2：在找对应顶点、对应边、对应角问题上谁还有别的体会？

预设：公共边一般是对应边；有对顶角的，对顶角一般是对应角，公共角一般是对应角等.

设计意图：在教学中充分发挥集体的力量，遇到与其他知识融合的题目，要给学生足够的思考时间，多让不同学生发表意见，延长后进生思考的时间.

教学环节（三）拓展小结

（1）全等三角形的对应边相等，对应角相等；

（2）全等三角形的周长相等；

（3）面积相等的三角形是全等三角形；

（4）全等三角形的面积相等.

预设解答：（1）对；（2）对；（3）错，让学生举一个反例说明；（4）对.作出正确判断需要学生从重合、形状和大小相同这些角度认识才行.

设计意图：在全等三角形性质的基础上拓展.教学时还可以问其他问题，如全等三角形对应角的平分线、对应边上的中线、对应边上的高有什么关系，甚至可以提出全等三角形中对应的线段有什么关系.

教学环节（四）布置作业（略）

二、教学立意的进一步解读

1.从生活经验出发，但不停留、不纠结于生活现实

从上面课例可见，我们从生活图形、折纸操作等活动出发，引入新知.这些生活经验作为情境，在课堂实施时并不停留，也不纠结，而是尽快推进、抽象出全等三角形，研究全等三角形的概念、对应边、对应角，学习更有数学味的平面几何概念.

2.从标准图形到变式图形，重视对应元素的训练

在全等三形的标准图形、定义新概念及对应元素之后，我们安排一系列的变式图形，通过PPT渐次呈现，引导学生思维参与、辨析对应，有效训练非标准全等图形的对应边和对应角.根据教学经验，学生如果只是理解标准图形的对应关系，而对于变式图形适应性不好，则在后续几何学习中就难以发现全等，影响思路获取和解题速度.

3.预设开放问题，促进学生独立思考后展示交流

在不同的教学环节，我们都注意预设开放问题，并安排学生先独立思考，接着在小组内交流讨论，最后大组展示交流，这样追求了由开放题走向“开放的数学教学”（郑毓信语），也是日本著名教育学者佐滕学倡导的让学生从“互相说”走向“互相听”.

1.章建跃.创新推动改革，全面提高教育质量——暨“第九届初中青年数学教师优秀课展示与培训活动”总结［J］.中国数学教育（初中），2016（4）.

2.周红娟.从操作走向思考，从“参观”走向“探索”——“等腰三角形的性质（第1课时）”教学与反思［J］.中学数学（下），2014（7）.

3.郑毓信.“开放的数学教学”新探［J］.中学数学月刊，2007（7）.Z