基于分形理论的长春都市圈城镇体系结构测度及其优化研究*

2016-12-27闫广华

长春教育学院学报 2016年12期

闫广华

闫广华

本文利用分形模型测算长春都市圈城镇体系的等级规模结构、随机集聚结构、空间相关性结构，分析得出2015年长春都市圈城镇体系的豪斯道夫维数、随机集聚维数、关联维数分别为0.7134、1.3602和0.5617、0.6451，说明长春都市圈城镇体系结构具有明显的分形特征，验证了分形理论在都市圈城镇体系结构研究中的适用性。结果表明：分形维数可以作为都市圈城镇体系结构研究的有力工具；长春都市圈中心城市垄断性强，缺少中间位序的城镇，城镇等级规模结构不合理；长春都市圈城镇体系在随机集聚结构上形成了以长春市为中心呈凝聚态分布的都市圈城镇空间结构；长春都市圈城镇空间关联程度较好，彼此相互联系程度较强。在测算的基础上，提出了长春都市圈城镇体系结构优化的对策。

城镇体系；城镇结构；分形理论；长春都市圈

都市圈是由主要城镇组成的经济、社会联系比较紧密的经济集合体，通常由一个或多个中心城市及其在地域上紧邻的若干核心城镇组成，核心城镇与中心城市具有紧密的经济联系和社会联系[1]。都市圈是一个开放的经济系统，中心城市与核心城镇间及核心城镇间不断地进行着物质、信息、能量的交换、流动与传递[2]。都市圈内不同规模等级和职能差异的城镇间不断相互作用，使得都市圈内城镇形成了具有紧密联系且具有一定结构的有机整体，即都市圈城镇体系[3]。城镇体系作为城市地理学的研究对象，引入新的量化方法，并加以应用扩展具有重要的意义[4]。20世纪70年代曼德尔布罗特开创的分形几何理论于90年代初开始应用于中国的城市地理学研究，分形理论能够刻画城镇体系的空间复杂性[4]，广泛应用于省域[5]、市域[6,7]、县域[8,9]、城市群[10]或者其他一些特定经济区[11,12]的城镇体系的分析研究。目前，国内外对都市圈城镇体系的分形研究主要集中于城镇规模等级分布和空间分布特征等方面，最典型的如刘继生、陈彦光等运用豪斯道夫维数、集聚维数、网络维数和空间关联维数对城镇体系结构进行研究，并在方法上提出或总结出一整套分形算法[13,14]。

长春市作为东北地区的核心城市，长春都市圈已经形成，是融入国家“一路一带”开放战略的重要节点。本文从都市圈的内涵出发，以经济联系的视角，利用分形理论定量分析长春都市圈城镇空间结构的分形特征，并提出长春都市圈城镇空间结构优化的策略，以期为长春都市圈城镇体系结构优化及相关理论和实证研究提供一定的参考。

一、研究的区域概况

都市圈中心城市和核心城镇构成了都市圈的城镇体系，当前，国内对都市圈的研究都是以县市域作为最小地理单元，造成各都市圈地域范围普遍过大，实际上是对城市群而不是对都市圈的研究，不能从本质上反映都市圈内涵[1]。而韩刚、袁家冬首次以建制乡镇作为最小地理单元，从经济联系的角度界定了长春都市圈的范围[15]，准确把握都市圈作为由相互联系较为紧密城镇体系构成的一种经济圈、社会圈和势力圈的本质内涵。因此，本文采用韩刚、袁家冬界定的长春都市圈范围[15]，构建以建制乡镇为最小地理单元的都市圈城镇体系（见表1）。长春都市圈城镇体系由34个城镇构成，其中，县市区5个，建制乡镇29个。长春都市圈平均半径约为57km，总面积约为10206.73km2，人口总量约为555万人[15]。

表1 长春都市圈城镇体系

二、研究的模型与方法

（一）城镇体系等级规模测度模型——豪斯道夫（Hausdoff）维数

1.豪斯道夫维数。豪斯道夫维数常用于描述都市圈城镇等级规模，定义：都市圈内城镇数量N（r）与城镇规模大小r成幂函数关系，可以用如下公式表示[16]：

对公式（1）进行对数运算，得如下（2）方程：

其中：D为豪斯道夫维数，C为常数。

2.捷夫（Zipf）公式的引入。都市圈的城镇体系具有等级规模特征，所以都市圈城镇服从位序—规模分布（即Zipf公式）[17]：

对上式（3）两边去对数，可以得下式：

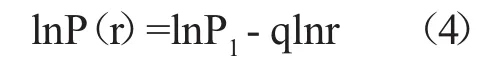
式中P1为都市圈内最大城镇人口数，r为城镇位序（r=1，2，3…n），p（r）为第r位城镇的人口数。

Zipf公式和Hausdorff公式相似，都服从幂函数定律，也都具有分形含义，所以Zipf公式也是一种分形模型，其中q是豪斯道夫维数D的倒数，即：D=1/q或q=1/D[18]。其意义如下：

当D=q=1时，都市圈中心城市与最小核心城镇人口数的比值等于都市圈内城镇体系的数量，这是最优分布状态；当D＜1，q＞1时，都市圈中心城市人口数明显多于其他核心城镇，中心城市处于垄断地位，都市圈内城镇间人口有较大差异；当D＞1，q＜1时，都市圈人口在各城镇间均衡分布，且中间位序的城镇数量比较多，都市圈城镇体系分布较集中；当D→0，q→∞时，都市圈内人口都集中在一个城市中；D→∞，q→0时，都市圈内所有城镇人口数量一样多，后两种属于极端情况，在现实中不存在。

（二）城镇体系随机集聚测度模型——集聚维数

都市圈城镇体系随机集聚是指都市圈内城镇围绕中心城市的分布状态，都市圈核心城镇按某种规则围绕中心城市呈现出凝聚态的空间分布规律，从而表现出随机聚集的分形，因此可用几何模型来测度都市圈城镇体系的随机分布特征，一般用以半径为r的圆的范围内有N（r）个城镇，从而确立了r和N（r）间的关系，即有N（r）∝CrD，D为分维，因为半径r影响分维数值，可将其转化为平均半径，所以以都市圈内最大城市（中心城市）为重心，可定义城镇随机空间分布的平均半径RS[14]：即

式中RS为平均半径，S为城镇个数，ri为第i个城镇到（中心城市）的欧氏距离（也称重心距离，i=1,2,3,…,n），＜＞表示平均。

根据城镇体系随机集聚的分形特征，如果在一定时空条件下，平均半径RS与城镇个数S间有如下关系：RS∝S1/D或者为：S∝RSD，说明中心城市的吸引力呈现出分形的特征，可以对其进行双对数转化得到如下公式：

这里R0是一常数量，D是分维数，其地理意义为城镇体系围绕中心城市随机集聚的特征，故D被称之为集聚维数。

集聚维数D反映的是都市圈内核心城镇围绕中心城市的随机集聚特征，一般取维数2为参考值，当D＞2时，则表明都市圈内的城镇密度从中心城市向外围圈层呈递增的空间分布特征；当如果D=2时，则表明都市圈内的城镇密度从中心城市向外围圈层呈均匀变化的空间分布特征；当D＜2时，则表明都市圈内的城镇密度从中心城市向外围圈层呈递减的空间分布特征[14]。

（三）城镇体系空间相关性测度模型——关联维数

都市圈内的城镇间具有较强相互作用的特征，特别是中心城市与核心城镇间的相互作用更加明显，运用关联维数可以较好地模型都市圈内城镇间的相关性特征，其公式如下[14]：

式中N为都市圈内城镇数目，r为设定的距离，dij为都市圈内第i个城镇与第j个城镇之间的欧氏距离，H为Heaviside越阶函数，根据城镇空间分布的分形特征，则有：C（r）=rD，其中D为关联维数，反映的是都市圈内城镇与城镇间的相关性规律，D一般大于0小于2，D值越小，表明都市圈城镇间的相关性较强，城镇间联系紧密，相互间的作用也较强；D值越大，表明都市圈城镇间的相关性较弱，城镇间联系不紧密，相互间的作用也较弱城镇空间分布较分散；当D趋于0时，表明都市圈内的城镇集中在中心城市内；当D趋于2时，表明都市圈内城镇间的联系均匀。

若将公式（7）中的直线距离改为实际交通距离，可以得到都市圈实际交通的关联维数D′，直线距离关联维数与实际距离关联维数的比值称为牛鸦维数比，用d来表示：

公式（8）中d值若越趋于1，则表明都市圈内城镇间的交通通达性就越好，都市圈内城镇间的关联度就越高，反之就越低。

三、长春都市圈城镇体系结构测度

（一）长春都市圈城镇体系等级规模的分形分析

运用公式（4）对长春都市圈的城镇体系等级规模结构做分维测算，将长春都市圈内城镇按人口数量多少进行排序，得到长春都市圈城镇体系的位序—规模对应关系（r，P(r)），并对其做散点图及回归计算，得出：InP(r)=1.4017Inr+1. 418．R2=0.9814，q=1.4017，D=0.7134。

根据城镇体系等级规模分形指数的分析，长春都市圈城镇体系的豪斯道夫维数R2=0.9814＞0.95，表明长春都市圈等级规模分形模型拟合情况较好，分形特征较为明显。D=0.7134＜1，表明长春都市圈城镇体系规模分布整体上较为集中，城镇等级规模结构不合理，中心城市垄断性强，首位度指标高，没有特大城市和超大城市，缺少中间位序的城镇，小城镇数量较多，城镇体系规模等级差异显著，人口分布则集中于中小城镇且相对均衡，是一种低水平的不均衡分布格局。

（二）长春都市圈城镇体系随机集聚的分形分析

借助上述式（5）得出平均半径Rs（表2），并用式（6）得出（Rs，S）的散点图，并对其进行回归模拟，通过计算得出：lnRs=0.7352lnr+2.1732，D=1/0.7352=1.3602＜2，R2=0.9794。

长春都市圈城镇随机集聚维数D=1.3602＜2，R2=0.9794＞0.95，拟合情况较好，具有明显的分形几何特征，表明长春都市圈城镇围绕中心城市长春市呈集聚态分布，表现为城镇密度从中心城市长春市向四周呈递减的空间分布特征，越向四周中心城市长春市对核心城镇的吸引力减弱的速度就越快，中心城市长春市在长春都市圈城镇体系中处于垄断地位，对周围核心城镇的吸引和辐射作用显著；另外，受到中心城市长春市辐射的影响，农安、公主岭等核心城镇的发展较快，加速了对其周围城镇的城镇化速度，也使得这些核心城镇的周围地区受中心城市长春市的辐射影响减弱，即长春市对其周围城镇的吸引力衰减速度逐渐增大。

（三）长春都市圈城镇体系空间相关性的分形分析

根据相关性的分形模型，对长春都市圈地图矢量化，通过GIS测算出直线距离和实际交通距离，得到一个对称矩阵（如表3）（由于篇幅限制，只列举一部分数据），取步长△r=10km来取距离标度r，得出N(r)和N′(r（)如表4），用式（7）可以得到一系列点对。将点列标进行回归拟合，可以得到以直线距离为参数的关联维度数D=0.5617和实际交通距离为参数的关联维数D′=0.6451，进一步得到牛鸦维数比d=0.8707。

从计算看出。D和D′都小于1，相关系数R2都大于0.95，拟合情况较好，具有明显的分形几何特征，表明长春都市圈城镇空间联系比较密切，城镇空间分布相关性较好，城镇之间相互作用比较强。而且牛鸦维数比d=0.8707接近1，表明长春都市圈内城镇与交通网络之间比较发达，主要重点城镇大都分布在交通路线上，都市圈内城镇体系交通网络的通达性较高，城镇间联系较为紧密。

表2 城镇分布的重心距离r与平均半径Rs

表3 长春都市圈90个主要城镇间直线距离（实际交通距离）半角矩阵(km)

表4 尺度r及相应的直线距离和实际交通距离数目N(r)和N′(r（)km）

四、测度结果评价及优化对策

（一）主要测度结果评价

根据城镇体系等级规模分形指数的分析，长春都市圈城镇体系的豪斯道夫维数R2=0.9754，拟合情况较好，分形特征较为显著。因为D=0.7134＜1，表明长春都市圈城镇体系规模分布整体上较为集中，城镇等级规模结构不合理，中心城市垄断性强，首位度指标高，缺少中间位序的城镇，小城镇数量较多，城镇体系规模等级差距显著，人口分布则集中于中小城镇且相对均衡，是一种低水平的不均衡分布格局；长春都市圈城镇随机集聚维数D=1.3602＜2，R2=0.9794，拟合情况较好，具有明显的分形几何特征，表明长春都市圈城镇围绕中心城市长春市呈集聚态分布，表现为城镇密度从长春市向四周呈递减的空间分布特征，越向四周长春市对核心城镇的吸引力减弱的速度就越快，长春市在长春都市圈城镇体系中处于垄断地位，受其辐射的影响，农安、公主岭等核心城镇发展较快，加速了对其周围城镇的城镇化速度，也使得这些核心城镇的周围地区受长春市的辐射影响减弱，即长春市对其周围城镇的吸引力衰减速度逐渐增大；长春都市圈城镇关联维数D和D′都小于1，相关系数R2都大于0.95，拟合情况较好，具有明显的分形几何特征，表明长春都市圈城镇空间联系比较密切，城镇空间分布相关性较好，城镇之间相互作用比较强。而且牛鸦维数比d=0.8707接近1，表明长春都市圈内城镇与交通网络之间比较发达，主要重点城镇大都分布在交通路线上，都市圈内城镇体系交通网络的通达性较高，城镇间联系较为紧密。

（二）主要优化对策

长春都市圈城镇体系结构具有明显的分形特征，这是长春都市圈进一步发展的基础，结合其分形特征，对长春都市圈城镇体系结构的未来发展提出以下建议。

1.根据长春都市圈城镇规模分布表现为城镇之间规模等级差距明显，中间位序城镇数量少，小城镇数量较多的特征，建议适当扩大中心城市长春市的城市规模，带动都市圈城镇体系的整体发展；重点扩大中等城镇规模，选择农安、公主岭、九台和双阳作为长春都市圈二级中心城市的重点培养对象，加快推进其城镇化发展，壮大人口的面和点的集中，改善长春都市圈城镇体系规模结构。

2.根据长春都市圈城镇围绕长春市呈集聚态分布，且长春市对其他城镇吸引力衰减速度逐渐增大的特征，建议进一步强化长春都市圈中心城市的辐射带动作用，通过对其规模和职能的扩大和扩张，增强核心动力，从经济联系上增强长春对周围城镇的吸引力，扩大经济吸引范围，改善对其他城镇吸引力衰减速度逐渐增大的现象。

3.根据长春都市圈城镇间联系较为紧密，城镇空间分布相关性较好的特征，为实现长春都市圈城镇体系更加紧密的经济社会联系，建议进一步强化交通基础设施建设，提高城镇间的通达性，实现都市圈城镇间的经济一体化。

[1]闫广华.沈阳都市圈的范围及城镇空间分布的分形研究[J].地理科学，2016（1）：1-7.

[2]李斌.基于位序—规模法则与分形理论的重庆市城镇体系结构测度及其优化[J].资源开发与市场，2014（2）：167-169，216.

[3]夏维力，李博.陕西关中地区城镇等级规模结构分形研究[J].地域研究与开发，2006（4）：58-61.

[4]刘继生，陈彦光.河南省城镇体系空间结构的多分形特征及其与水系分布的关系探讨[J].地理科学，2003（6）：713-720.

[5]朱士鹏，徐兵，毛蒋兴.广西城镇体系空间结构分析研究[J].热带地理，2010（2）：178-182.

[6]杨晓楠，高晓东.基于分形理论的齐齐哈尔市城镇体系空间结构研究[J].吉林师范大学学报(自然科学版)，2008（1）：93-95.

[7]曹芳东，吴江，徐敏.基于分形理论的江苏省南通市城镇体系空间结构研究[J].人文地理，2010（5）：69-74.

[8]邹小硕，千怀遂，梁圆.基于分形理论县域城镇体系空间结构变化分析[J].生态科学，2015（3）：76-84.

[9]丁贤法.富宁县城镇体系空间结构及水系的分形研究[J].文山学院学报，2011（3）：113-116.

[10]邬文艳.呼包鄂城市群空间结构分析特征分析[J].河套大学学报，2011（4）：18-24.