供应链契约稳定性及其在期权博弈视角下的优化
2016-12-27刘琦铀张成科冷碧滨
刘琦铀, 张成科,冷碧滨
(广东工业大学经贸学院,广东 广州 510000;2.南昌大学管理科学与工程系,江西 南昌 330031)
供应链契约稳定性及其在期权博弈视角下的优化
刘琦铀1, 张成科1,冷碧滨2
(广东工业大学经贸学院,广东 广州 510000;2.南昌大学管理科学与工程系,江西 南昌 330031)
供应链契约作为一种有效的经营合作模式,已得到理论界和企业界广泛认同,并在实际的产业化经营中占据主导地位。由于市场需求及价格波动的不确定性引发的机会主义行为,导致契约在执行过程中存在逆向选择和道德风险,严重影响了产业化组织的运行效率。为探索供应链契约模式的稳定性并制定有效的优化策略,通过静态博弈模型得出供应链契约模式价格波动区间,进而深入分析了决策参数对契约稳定性的影响。在此基础上,借助期权市场的风险规避功能,寻求风险外化通道以协调契约主体间的利益冲突,为探索供应链契约模式中供应商的高违约率问题提供新的视角。
期权;博弈;供应链契约;稳定性
1 引言
供应链契约是指产品生产过程中,各参与主体(原材料供应商、制造商和分销商等)在利益驱动机理下,以合同、协议的形式结成的,围绕龙头企业(制造商)和各供应商之间的一种风险共担、利益共享的关系模式。在该合作模式下,供应商专门负责半成品的生产,龙头企业则负责半成品的加工和销售,一些龙头企业也向供应商提供相关的产前和生产过程中的服务,通过这种分工协作的方式,把传统生产、加工、销售等环节有效的实行专业化衔接,以达到利益共享的“双赢”目的。
供应链契约是契约理论在供应链中的一种表现形式,其概念最早由Pasternack[1]于1985年提出。此后,国内外学者针对该问题展开了大量研究,已有文献主要集中在以下几方面:(1)供应链契约综述性研究:Cachon[2]从不同的维度将供应链契约划分为正式和非正式契约、单周期和多周期契约、强制执行和自愿遵守契约等,并对回购契约、批发价格契约、数量弹性契约和收益共享契约的概念及优化条件进行了详细介绍,同时对供应链契约已有研究文献进行了详细综述;高峻峻等[3]对供应链协调与契约等问题的外部环境进行了简要分析,并对其研究进展进行了综述;在分析和归纳了供应链契约发展过程的基础上,杨德礼等[4]对几种典型的供应链契约问题建立了相关数学模型,最后指出了供应链契约的发展趋势。(2)最优定价与库存协调优化问题:孙会君等[5]用双层规划模型得出供需双方的利润可以通过制定合适的订购数量和折扣策略等来提高;在对供应链契约的一般订货模式和协调模式进行了详细分析的基础上,常良峰等[6]构建了买方需求确定下的卖方成本优化数学模型, 并将其与一致数量折扣与累积数量折扣的协作机制进行了对比分析;Narayanan等[7]研究了从同一个制造商购买商品的两个价格竞争的销售商的定价和订货量的均衡解。(3)供应链中信息不对称问题:供应链契约模式虽基于“风险共担、收益共享”的机制上构建,但作为独立的“经济人”的参与主体,当存在利益冲突时,彼此间往往会隐瞒有价值的信息,以期牟取私利,这无疑会与供应链契约合作“共赢”的初衷背道而驰。Corbett等[8]分别讨论了卖方成本在信息对称与不对称下,批发价契约、双方线性契约、随订货量变化的双方线性契约这三种契约共6种情况下,生产商、销售商和供应链的利润变化情况,以此得出信息的价值和不同契约的价值;通过引进基于惩罚和奖励的激励函数,张翠华等[9]研究了非对称信息下生产商与供应商之间的协同机制;通过构造一个两阶段的多任务委托-代理模型,马新安等[10]就供应链中核心企业对供应商进行供应活动和信息共享活动的最优激励问题进行了详细研究,并将其用来解释供应链中合作伙伴间关系的持续改善过程;索寒生等[11]运用委托-代理模型研究了信息不对称下供应商的最优回购策略。(4)供应链合作中创新投入和信息激励问题:Cho等[12]研究了制造商通过创新以减少单位产品生产成本,分别给出了收入分享契约、回购契约和二部分定价契约这三个供应链契约模式的协调优化策略。Gilbert等[13]研究得出制造商通过创新投入来降低产品成本,供应商在批发价格承诺下比不承诺下,更能有效的使供应链得到协调优化;通过将博弈论和信息经济学理论和方法引入到供应链契约模式中,黄祖庆等[14]研究了激励机制对供应商和零售商订货量及其收益产生的影响。
通过对已有文献的分析和归纳可知,供应链契约问题虽引起了国内外相关学者高度的重视,并展开了大量研究。然而,已有的研究大都讨论不同情况下供应链契约的协调优化问题,或仅对供应链合作的稳定性进行研究[15-16],却很少考虑市场波动引发的机会主义行为,从道德风险和逆向选择的角度,去考虑供应链契约模式的违约问题及稳定性优化。期权市场作为金融衍生品和投资者聚集的场所,因具有较完善的风险分散、转移和交易机制,能有效的降低风险的同时促进经济稳定运行。文章在已有研究基础上,将深入分析市场价格波动引发的机会主义行为,基于静态博弈理论模型,分析了供应链契约模式稳定性区间及其影响因素;最后,借助期权市场的风险规避功能,寻求风险外化通道以协调契约主体间的利益冲突,为探索供应链契约模式中供应商的高违约率问题提供新的视角。
2 供应链契约博弈及其稳定性分析
供应链契约模式以市场为导向,契约为纽带,来实现产品从产到销的垂直性分工过程。该模式以产业化的经营方式,形成“龙头”企业将产供销各不同环节市场内部化,通过组织边界的扩张,变市场外部交易为组织内部交易,从而节省交易费用(包括:信息搜索成本、交通成本、讨价还价成本等)。研究中通常将该模式简化为由一个制造商和一个原材料/半成品供应商组成的二级供应链,其中制造商是龙头企业且面临一个随机的市场需求;供应商是追随者且不存在资产专用性问题;产品订货周期较长且具有较大的时令性。在市场经济条件下,博弈双方都是基于风险中性和完全理想的“经济人”假设,契约的执行以利润最大化为原则。当市场波动较大,利益受损一方超出其在供应链契约模式下所获收益时,逆向选择和道德风险必然会存在。因此,若缺乏有效的风险分担和行为约束机制,供应链契约模式在契约执行过程中所面临的高违约率问题,势必会成为制约其发展的重要因素。为了便于问题的描述,首先对相关符号定义如下表1所示:

表1 模型相关参数符号设定
现假设在t=0时点,契约双方签订了一份合同,由于契约双方是一种长期的战略性合作,因此,在合同到期的t=1时点,双方决策时不仅要权衡当下的收益,还要考虑将来可能获益的折现情况。设供应商和制造商在合同执行时,考虑到将来t=2到t=n时期选择合同交易或市场交易所获收益的贴现值分别为πc1,πm1,πc2,πm2[17]:
(1)
(2)
(3)
(4)
在合同到期的t=1时点,综合考虑契约双方履约(O)、违约(D)情况下即期收益及未来可能获益的贴现值,可得该时点双方得益矩阵如下表2所示:

表2 供应链契约模式在t=1时点双方得益矩阵
由于供应链契约模式下,各决策主体选择履约或违约行为主要取决于各自对其成本收益的比较分析,故依据产品市场价格波动,存在以下两种情况:
(1)当市场行情不好,单位产品市场价格低于契约合同中的约定价格,即Pm-Pc<0。此时,供应商倾向于履约,而制造商则倾向于违约而直接从市场上购买原材料和半成品,但契约双方综合考虑到惩罚系数和未来合作中可能获益等因素,都有选择“履约”和“违约”策略的可能。由于通过供应链契约模式交易,制造商有稳定的半成品货源,而供应商有稳定的产品销路,且可以节省各自的交易成本。因此,在t=i时点,双方对下一期(t=i+1)通过供应链契约模式进行交易的即期效用都不小于下一期双方通过市场交易的即期效用。即:
UG(t=i)(Pc-C+c1)t=i+1≥UG(t=i)(Pi-C)t=i+1
(5)
UZ(t=i)(K+Pi-Pc+c2)t=i+1≥UZ(t=i)Kt=i+1
(6)
令λ1=πc1-πm1,λ2=πc2-πm2,g=UG(t=i)(Pc-C+c1)t=i+1-UG(t=i)(Pi-C)t=i+1≥0,z=UZ(t=i)(K+Pi-Pc+c2)t=i+1-UZ(t=i)Kt=i+1≥0。则由式(1-6)可知,在t=1时刻,供应商和制造商分别考虑通过供应链契约模式和在市场上进行交易的即期效用差为:
(7)
(8)

UG(OG,OZ)-UG(DG,OZ)=(Pc-C+c1)q+πc1-(Pm-C-d1)q-πm1=(Pc-Pm+c1+d1)q+qg*>0
(9)
UG(OG,DZ)-UG(DG,DZ)=(Pm-C+d2)q+πc1-(Pm-C+d2-d1)q-πm1q+qg*>0
(10)
由式(9)和(10)可知,在市场行情较差时,UG(OG,SZ)-UG(DG,SZ)>0。即不管制造商的策略是履约还是违约,履约为供应商的占优策略。此时有:
UZ(OZ,OG)-UZ(DZ,OG)=(K+Pm-Pc+c2)q+πc2-(K-d2)q-πm2=(Pm-Pc+c2+d2+z*)q
(11)
由式(11)可得,当-c2-d2-z* (2)当市场行情较好,单位产品市场价格不小于契约中的约定价格,即Pm-Pc≥0时,同理,由表2和式(8)可得: UZ(OZ,OG)-UZ(DZ,OG)=(K+Pm-Pc+c2)q+πc2-(K-d2)q-πm2=(Pm-Pc+c2+d2)q+qz*>0 (12) UZ(OZ,DG)-UZ(DZ,DG)=(K+d1)q+πc2-(K+d1-d2)q-πm2=d2q+qz*>0 (13) 由(12)和(13)可知,当市场行情较好时,UZ(OZ,SG)-UZ(DZ,SG)>0。即不管供应商的策略是履约还是违约,履约为制造商的占优策略。此时有: UG(DG,OZ)-UG(OG,OZ)=(Pm-C-d1)q+πm1-(Pc-C+c1)q-πc1=(Pm-Pc-d1-c1)q-qg*=(Pm-Pc-d1-c1-g*)q (14) 由(14)可知,当Pm-Pc>c1+d1+g*时,供应商的占优策略是违约,此时(违约,履约)为供应商和制造商博弈的均衡解;反之,当Pm-Pc 综上分析可知,供应链契约模式下契约双方决策策略随产品市场价格波动情况用坐标轴表示如下图1所示。图中以衡量市场价格波动的指标Pm-Pc为坐标,分别用蓝色和红色标识二者的履约、违约区间,其中履约区间用实线阴影部分标识,违约区间用虚线标识。由图可知,供应链契约模式随价格波动双方履约的稳定区间为[-c2-d2-z*,c1+d1+g*],价格的波动一旦偏离该区间,即当Pm-Pc∈(-∞,-c2-d2-z*)时,则制造商会违约;当Pm-Pc∈(c1+d1+g*,+∞)时,则供应商会选择违约。 图1 供应链契约模式下双方履约、违约区间示意图 为了便于问题的描述,假设Pm在Pc上下以振幅X波动,且X~N(μ,1),其分布函数为F(x),φ(x)~N(0,1)的标准正态分布,供应链契约的履约率为η,则由图1可知: (15) 由式(15)可以看出,供应链契约履约率公式的关键参数有期望值、交易节省费用、惩罚系数和参与供应链契约长期合作预期得益偏好值等,现基于这些参数对供应链契约模式的稳定性做进一步分析。 3.1 期望值μ对供应链契约模式稳定性影响 为了求解期望值μ对供应链契约模式稳定性的影响,在式(15)中分别将η对μ求一阶和二阶偏导数,并令其一阶偏导数为零: (16) (17) (18) 3.2 交易节省费用、惩罚系数、长期合作偏好值对供应链契约模式稳定性影响 为了探讨契约双方所节省的交易费用、惩罚系数和参与供应链契约长期合作预期得益偏好值等因素对契约稳定性的影响,将式(15)分别对各影响因素求偏导数可得: (19) (20) 由式(19)和(20)可知,履约率η对各影响因素求一阶偏导数所得结果均大于零,由此可知,履约率η为各影响因素的增函数。即增大供应链契约合作所节省的交易费用、长期合作预期得益的偏好值和惩罚系数,在一定程度上能防止契约在执行过程中的违约现象,提高契约的稳定性。 供应链契约合作所节省的交易费用主要影响因素包括信息搜索费用、交通费用和讨价还价的费用等;而供应链契约双方长期合作预期得益的偏好值,除了受市场价格,合同执行价格和交易节省费用等影响因素外,还受市场贴现率r的影响。r的值越高,预期的收益折现值也就越大,各主体参与供应链契约模式预期得益的偏好值也就越大。违约惩罚系数包括有形的违约惩罚金和无形的信誉损失给企业品牌形象等带来的可预期的其它损失(尤其对于大的企业),现对供应商和制造商的惩罚系数分析如下: 对于供应商而言,由于(1)它是追随者,资产规模较小,当有形的惩罚金额数量太大以至于无法承受时,供应商可能会申请破产,因此有形的惩罚金额过大可能会成为不可信承诺。而制造商由于面对较多的原材料和半成品供应商,当多个供应商违约事件发生时,诉讼费用较大,且法院的介入也难以保证契约的有效执行,因此制造商会面临一个新的“起诉”和“沉默”策略间的博弈。(2)供应商的资产规模小,尚未形成品牌价值,违约对他们的信誉损失造成的可预期损失较小。因此,供应商的惩罚系数d1较小。 作为龙头企业的制造商,由于(1)资产规模较大,因此,为避免违约事件的发生,契约在签订过程中可设置较大的单位产品惩罚金,当其违约时,法院的介入能确保惩罚行为的可执行性;(2)具有一定的和品牌效应,因此违约时无形的信誉损失给制造商所带来的可预期的其它损失较大。因此,制造商的惩罚系数d2较大,d2>>d1。 基于这样的前提,文章假设d2足够大,即制造商违约的代价很大,可以忽略制造商违约的可能,而仅对供应商单方面违约事件发生时,探讨如何利用期权市场的风险规避功能,来有效解决供应链契约模式中供应商的高违约率问题。 由于契约主体双方履约与否,主要取决于市场价格偏离契约执行价格的幅度以及违约可能带来的成本间的权衡。供应链契约模式稳定性的影响因素较多,而市场风险的存在是导致违约问题发生的最根本原因。契约主体的信誉度提升、经济惩罚系数的提高以及违法执行力度加强等治理机制的完善,虽在一定程度有助于履约率的提高,却难以从根本上遏制违约事件的发生。因此,解决供应链契约模式违约问题的关键是借助现代金融市场体系的风险处理与防范功能,以设计合理的市场风险分担机制,将供应链契约模式的经营风险在金融市场上进行有效化解。 在期货概念基础上衍生出来的期权理论始于金融领域,随着供应链契约研究的发展,期权理论因具有较好的风险规避功能被国内外学者所青睐,并成功应用到供应链契约模式的稳定性协调优化中。期权是指买方向卖方支付一定的权利金(期权价)而拥有的,在未来一段时间内(指美式期权)或未来某一特定时期(指欧式期权),以协议的价格(执行价格)向期权卖方购买或出售一定数量特定标的物的权利,但却不负有必须买进或卖出的义务。由上节分析可知,当Pm-Pc>c1+d1+g*时,供应商的占优策略是违约。因此,为了有效提高履约率,契约双方在合同签订的同时,可以在期权市场上同时买入一份数量相同的,期权执行价格为契约执行价格Pc的看涨期权。当供应商违约时,由于购买了执行价为Pc的看涨期权,此时,制造商执行看涨期权,将在期权市场以固定的协议价格买入标的物或获得相应标的物的市场差价,以维持正常生产运行。双方约定若制造商单方面违约时,则制造商应承担相应的期权费用。通过引入期权这一有效的金融衍生工具,供应商最大的可预见损失为期权费,却可以享受产品价格上涨所获得的收益,制造商则可以有效规避供应商违约所带来的损失。 假设供应商购买期权以规避市场风险在合同执行的t=1时刻,考虑到未来t=2到t=n时期可能获益的贴现值为πo1: (21) 由此可得契约双方的得益矩阵如下表3所示: 表3 期权博弈视角下供应链契约模式在t=1时点双方得益矩阵 由于在t=i时点,供应商对下一期(t=i+1)通过供应链契约模式进行交易的即期效用都不小于下一期通过市场交易的即期效用。即: UG(t=i)(πo1)t=i+1≥UG(t=i)(πm1)t=i+1 (21) 由上表3和式(21)可知: UG(OG,OZ)-UG(DG,OZ)=[max(Pc,Pm)-C-Co+c1)]q+πo1-(max(Pc,Pm)-C-d1-Co)q-πm1=(c1+d1)q+UG(t=i)(πo1-UG(t=i)(πm1>0 (22) UG(OZ,DZ)-UG(DZ,DZ)=[(max(Pc,Pm)-C+d2)]q+πo1-[(max(Pc,Pm)-C+d2-d1-Co)]q-πm1=(d1+Co)q+UG(t=i)(πo1-UG(t=i)(πm1>0 (23) 由(22)和(23)可知,UG(OG,SZ)-UG(DG,SZ)>0,即不管市场条件如何,履约始终为供应商的占优策略。由上表3和式(8)可得: UZ(OZ,OG)-UZ(DZ,OG)=(K+Pm-Pc+c2)q+πc2-(K-d2-Co)q-πm2=(Pm-Pc+c2+d2+Co+z*)q (24) 由(24)式可得,当Pm-Pc>-c2-d2-Co-z*时,制造商的占优策略是履约,此时(履约,履约)为供应商和制造商的均衡解;反之,当Pm-Pc<-c2-d2-Co-z*,制造商的占优策略是违约,此时,(履约,违约)为供应商和制造商的博弈均衡解。由此可得,供应链契约模式下契约双方决策策略随产品市场价格波动情况用坐标轴表示如下图2所示: 图2 期权博弈视角下供应链契约双方履约、违约区间示意图 图中可知,基于期权博弈理论的供应链契约优化模式的履约区间为[-c2-d2-Co-z*,+∞)。 作为龙头企业的制造商,由于其资产规模较大且具有一定品牌效应,因此,违约时无形的信誉损失给企业品牌形象等带来的可预期的其它损失较大;为了杜绝契约执行过程中制造商违约问题发生,契约签订过程中可以对制造商设置较大的单位产品有形违约惩罚金,使违约系数d2足够大,从而遏制制造商违约事件的发生。即当d2→∞时,-c2-d2-Co-z*→-∞,此时,可将期权博弈视角下的供应链契约优化模式的履约区间视为(-∞,+∞)。 由此可知,期权博弈视角下的供应链契约模式,使供应商能有效规避市场风险的同时享受市场价格上升所带来的利益。因此,供应商可以进一步扩大生产规模以降低生产成本的同时提高收益。 对于制造商而言,该模式能保证货源稳定性的同时提高收益,使企业稳步、高效运转。 (1)当市场行情较差,即Pm-Pc<0时,由(9)和(10)式可得: UG(OG,OZ)-UG(DG,OZ)==(Pc-Pm+c1+d1+g*)q=(Pc-Pm+3.453)×100>0 UG(OG,DZ)-UG(DG,DZ)=(d1+g*)q=(1.5+0.853)×100=235.3>0 即在市场行情较差时,不管制造商的策略是履约还是违约,履约为供应商的占优策略,即UG(OG,SZ)-UG(DG,SZ)>0,此时有: UZ(OZ,OG)-UZ(DZ,OG)=(Pm-Pc+c2+d2+z*)q=(Pm-Pc+1.3+10+1.706)×100 由于市场价格在合同价格以幅度X(Pm-Pc∈[-5,+∞))波动,而UZ(OZ,OG)-UZ(DZ,OG)>0时,Pm-Pc>-13.006。由此可知,当违约系数d2取值较大时,UZ(OZ,OG)-UZ(DZ,OG)>0始终成立。即制造商的违约事件不可能发生,此时(履约,履约)为供应商和制造商唯一的均衡解。 鞍山地区依据《建筑抗震设计规范》2016版该区域为设计地震烈度7度,设计分组为第二组,设计基本地震加速度0.10g。所以调整系数β为0.95,液化判别标准贯入锤击数基准值N0为7。对9个钻孔17层砂土具体计算结果统计如下: (2)当市场行情较好,即Pm-Pc≥0时,由(12)和(13)式可得: UZ(OZ,OG)-UZ(DZ,OG)=(Pm-Pc+c2+d2+z*)q=(Pm-Pc+13.006)×100>0 UZ(OZ,DG)-UZ(DZ,DG)=(d2+z*)q=(10+1.706)×100=1170.6>0 即在市场行情较好时,不管供应商的策略是履约还是违约,履约为制造商的占优策略,即UZ(OZ,SG)-UZ(DZ,SG)>0,此时有: UG(DG,OZ)-UG(OG,OZ)=(Pm-Pc-d1-c1-g*)q=(Pm-Pc-3.453)×100 若UG(DG,OZ)-UG(OG,OZ)≥0时,即Pm-Pc≥3.453时,供应商的占有策略是违约,此时,(违约,履约)为供应商和制造商的博弈均衡解;若UG(DG,OZ)-UG(OG,OZ)<0时,即0 综上可知,当制造商违约系数d2取值足够大,制造商的违约事件不可能发生,此时,它的履约区间为Pm-Pc∈[-5,+∞);而供应商的违约和履约区间分别为Pm-Pc∈(3.453,+∞),Pm-Pc∈[-∞,3.453)。可知,供应链契约模式下契约稳定的价格波动区间为:Pm-Pc∈[-5,3.453],当价格波动的区间一旦偏离该区间范围,供应商则有违约的动机。 由于UG(t=i)(πo1)t=i+1≥UG(t=i)(πm1)t=i+1,则由(22)和(23)式可知: UG(OG,OZ)-UG(DG,OZ)=(c1+d1)q+UG(t=i)(πo1-UG(t=i)(πm1=260+UG(t=i)(πo1-UG(t=i)(πm1>0 UG(OZ,DZ)-UG(DZ,DZ)=(d1+Co)q+UG(t=i)(πo1-UG(t=i)(πm1>0=270+UG(t=i)(πo1-UG(t=i)(πm1>0 由上可知,UG(OG,SZ)-UG(DG,SZ)>0,即不管市场条件如何,履约始终为供应商的占优策略。由式(24)可得: UZ(OZ,OG)-UZ(DZ,OG)=(Pm-Pc+c2+d2+Co+z*)q=(Pm-Pc+13.206)×100 由上可知,当Pm-Pc≥-13.206时,制造商的占优策略是履约;反之,当Pm-Pc<-13.206时,制造商的占优策略是违约。由于Pm-Pc∈[-5,+∞),因此,Pm-Pc<-13.206不可能成立,即当d2足够大时,制造商的违约事件不可能发生,履约为唯一可选策略。由此可知,当制造商的惩罚系数d2足够大,无论市场价格如何波动,(履约,履约)为供应商和制造商的博弈均衡解。即期权博弈视角下的供应链契约模式能有效的化解市场风险,从根本上遏制由于市场价格波动而引发的供应商高违约率问题。 契约稳定性是减少交易成本,使供需双方有稳定的销路和货源、提高供应链反应速度的根本需要。本文以静态博弈模型为基础,通过对市场价格偏离契约执行价格的幅度以及违约可能带来的成本间的权衡,得出契约主体履约区间及相关因素对契约稳定性的影响。数值分析表明,契约主体信誉的提升、经济惩罚系数的提高、违约执行力度的加强等治理机制的完善,虽在一定程度有助于履约率的提高,却难以从根本上消除市场风险,遏制违约事件的发生。解决供应链契约模式高违约率问题的关键是借助金融市场的风险处理与防范机制,寻求风险外化通道以协调契约主体间的利益冲突,将市场风险在期权市场上进行有效化解。通过支付一定的期权权利金,期权博弈视角下的供应链契约模式使供应商能有效规避市场风险的同时享受市场价格上升所带来的利益;而制造商能保证货源稳定性的同时提高收益,使企业稳步、高效运转。 文章假设作为龙头企业的制造商规模较大、信誉度较高,通过对其设定较大的违约系数,以简化问题复杂度而对制造商的违约事件不加以考虑。如果放宽这一假设前提,制造商的企业规模和信誉度也较小,此时,若市场风险较大且对制造商不利时,它也会像供应商一样选择违约。通过供应链契约模式,供应商把产品价格风险转移给制造商,在以后的研究中,需要进一步契约主体双方都违约时,如何利用期货、期权等金融衍生工具进行套期保值以规避市场风险。即除了到期权市场进行套期保值以规避产品价格上升所带来的市场风险外,制造商在和供应商签订契约的同时再到期货市场进行套期保值,以化解产品价格降低所带来的市场风险,得到更准确的结论,这是未来需进一步研究和解决的问题。 [1] Pasternack B A.Optimal pricing and returns policies for perishable commodities [J].Marketing Science,2008,27(1):133-140. [2] Cachon G P. Operation and managements science: Supply chain management [M].North-Holland,2003. [3] 高峻峻,王迎军,郭亚军,等.供应链管理模型的分类和研究进展[J].中国管理科学,2005,13(5):116-125. [4] 杨德礼,郭琼,何勇,等.供应链契约研究进展[J].管理学报,2006,3(1):117-125. [5] 孙会君,高自友.基于差分的数量折扣条件下订货策略优化模型[J].管理科学学报,2004,7(2):18-23. [6] 常良峰,黄小原,卢震.一类供应链的Stackelberg主从对策问题研究[J].中国管理科学,2002,10(6):44-47. [7] Narayanan V G, Raman A, Singh J. Agency costs in a supply chain with demand uncertainty and price competition[J].Management Science,2005,51(1):120-132. [8] Corbett C J, Zhou Deming, Tang C S. Designing supply contracts: contract type and information asymmetry[J].Management Science,2004,50(4):550-559. [9] 张翠华,任金玉.非对称信息下基于惩罚和奖励的供应链协调机制[J].中国管理科学,2006,14(3):32-37. [10] 马新安,张列平,田澎.供应链中的信息共享激励:动态模型[J].中国管理科学,2001,9(1):19-24. [11] 索寒生,金以慧.非对称信息下供需链中供应商的回购决策分析[J].控制与决策,2004,19(3):334-337. [12] Cho O R K, Gerchak Y. Supply chain coordination with downstream operating costs:coordination and investment to improve downstream operating efficiency [J].European Journal of Operational Research,2005,162(5):762-772. [13] Gilbert S M, Cvsa V. Strategic commitment to price to stimulate downstream innovation in a supply chain[J]. European Journal of Operational Research,2003, 150(3):617-639. [14] 黄祖庆,达庆利.基于一类两级供应链的激励机制策略研究[J].管理工程学报, 2005(3):28-31. [15] 刘朝刚,马士华.供应链合作的稳定性分析[J].科技管理研究,2007,(2):238-241. [16] 宁钟,戴俊俊.期权在供应链风险管理中的应用[J].系统工程理论与实践,2005,(7):49-54. [17] 曾荣浩,杜跃平.基于现值法的供应链合作伙伴关系稳定性研究[J].情报杂志,2006,(2):75-77. [18] 涂国平,冷碧滨.基于博弈模型的“公司+农户”模式契约稳定性及模式优化[J].中国管理科学,2010,18(3):148-157. 第十八届中国管理科学学术年会征文通知 第十八届中国管理科学学术年会将于2016年11月11日-13日在西安交通大学召开,欢迎广大专家学者、科技和教育工作者积极投稿并参加会议。 主办单位:中国优选法统筹法与经济数学研究会 西安交通大学 中国科学院科技政策与管理科学研究所 《中国管理科学》编辑部 支持单位:陕西省科学技术厅 陕西省发展和改革委员会 承办单位:西安交通大学管理学院 会议主题:大数据驱动的管理创新 征文范围: 优选法与优化管理 统筹法与项目管理 经济数学与低碳经济 大数据技术与方法 数据驱动的过程管理决策 健康管理与大数据医疗 金融工程与风险管理 工业工程与运作管理 信息系统与商务智能 物流与供应链管理 营销工程与服务科学 战略管理与认知决策 数据挖掘与知识管理 人力资源与组织绩效管理 创业与小微企业管理 安全与应急管理 资源型产业发展模式 能源与环境管理 公共管理与复杂系统管理 战略型新兴产业与产业金融 企业管理创新理论与实践 大数据与智慧城市(智慧交通、智慧养老、智慧社区) 大数据金融产业研究 征稿要求: ▲ 未在其它学术会议、论文集和刊物上公开发表过。 ▲ 文章具体格式可参照《中国管理科学》近期期刊。 ▲ 来稿篇幅要求5-8页(5页以内版面费600元,超过5页每增加一页加收版面费150元)。 ▲来稿注明:征文类别(从征文范围中选择一个接近的类别填写)、作者简介、单位、通讯地址、邮编、联系电话、E-mail地址。 截稿日期:2016年6月30日 录用通知:2016年8月15日 论文出版: 出版《中国管理科学》专辑(已被CNKI数字图书馆全文收录(www.cnki.net)),以国家正式出版物的方式出版发行,书中将收录通过评审录用的论文。并在会前将所有录用论文的长摘要编辑成册《第十七届中国管理科学学术年会论文摘要》 。 大会设优秀论文报告奖: 会议论文通过评审录用后可参加本届年会专题会议的交流评议,获《优秀论文报告奖》的论文将颁发获奖证书并安排在《中国管理科学》正刊发表,直接列入2017年刊登计划。 会议具体情况请登陆中国优选法统筹法与经济数学研究会网站:www.scope.org.cn;中国管理科学网站:www.zgglkx.com及中国学术会议网站:www.zgglkxnh.conf.cnki.net 。 大会秘书处: 联 系 人:傅继良、张玲 E-mail:shuangfa@casipm.ac.cn联系电话:010-62542629 西安交通大学联系人:吕文静、贾峰菊E-mail:jia_fj@mail.xjtu.edu.cn电话:029-82665096 中国优选法统筹法与经济数学研究会 2016年2月3日 The Stability of Supply Chain Contract and Its Optimization Under the Perspective of Option Game LIU Qi-you1, ZHANG Cheng-ke1,LENG Bi-bing2 (1.School of Economics and Commerce, Guangdong University of Technology,Guangzhou 510000, China;2.Department of Management Science and Engineer,Nanchang University,Nanchang 330031, China) A supply chain contract mode is a market-oriented vertical product integration process from its production to sales. In the market economy, the execution of contracts is to maxmize profits, based on the assumptions of risk-neutral and fully rational game players. However, in a much volatile market, adverse selection and moral risk will occur when one player get losses under the normal supply chain contract mode. Therefore, high default rates for supply chain contracts will be vital to refrain from their executions without effective risk-sharing and behavior-constraint mechanisms. In this paper, the stability of supply chain contract modes are studied and optimization strategies are offered. Firstly, static game model is explored to obtain scopes of price fluctuations for supply chain contract modes. Secondly, detailed analysis is given to the impact of decision parameters on the stability of contract. Finally, a risk externality channel is sought to concert profit conflicts between contract parties, with the help of risk hedge function in options market. This no doubt offers a new prospective to solve the problem os high default rates in supply chain contract modes. Results show that such governance mechanisms as higher credits of contract parties, higher economic punishment coefficients, or more powerful default implementation measures, can help improve performance rates to some extent. But they can hardly eradicate market risks and occurrence of defaults. To solve high default rates for supply chain contract modes, it is vital to seek risk externality channel to coordinate the conflict of interest, with the help of risk treatment and prevention mechanisms in financial markets. As a result, market risk for supply chains can effectively be resolved in the options markets. From perspective of option games, by paying certain premiums under supply chain contract modes, supplier can effectively avoid market risks and meanwhile obtain benefits of rising prices. Manufacturers can fulfil steady efficient operations with higher incomes and more reliable supply stability. option; game; supply chain contract; stability 1003-207(2016)03-0071-09 10.16381/j.cnki.issn1003-207x.2016.03.009 2014-06-04; 2014-12-12 国家自然科学基金资助项目(71171061);广东省自然科学基金项目(S2011010004970) 简介:刘琦铀(1983-),男(汉族),江西萍乡人,广东工业大学经贸学院博士后,研究方向:管理博弈论及其应用、先进制造管理、智能计算,E-mail:liuqiyou1215@163.com. F274 A
3 供应链契约模式稳定性及影响因素分析

4 期权博弈视角下的供应链契约模式优化


5 算例分析
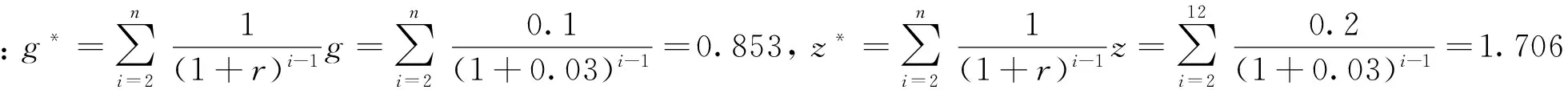
6 结语
