联合促销下双渠道VMI供应链的竞争与协调

王道平，张博卿，李小燕

(北京科技大学东凌经济管理学院， 北京 100083)



联合促销下双渠道VMI供应链的竞争与协调

王道平，张博卿，李小燕

(北京科技大学东凌经济管理学院， 北京 100083)

本文在双渠道VMI供应链中，假设制造商和零售商分别处于领导者和追随者的地位，考虑了制造商通过联合促销协调供应链上下游的策略以及双渠道需求之间的搭便车效应，以此为背景建立了制造商和零售商之间的Stackelberg博弈模型，并通过拉格朗日乘数法求解出了制造商的最优发货策略和零售商的最优定价与促销策略。研究发现制造商开辟网上渠道直销产品后，零售商缺货时间比例增大。进一步研究发现，制造商承担促销成本的比例，双渠道之间的搭便车效应对供应链成员的决策和利润有显著影响。另外，双渠道的需求越不稳定，则制造商开辟网上销售渠道后获利越高，同时零售商的利润越低。最后，通过算例验证了模型的有效性并对模型中主要参数进行了灵敏度分析。

联合促销；双渠道供应链；供应商管理库存；供应链协调

1 引言

随着互联网技术的发展和消费者消费观念的改变，越来越多的制造企业在传统零售商销售渠道的基础上开辟了网上直销渠道，以便直接向消费者销售产品。网络直销渠道的开辟有助于制造商扩大产品销量和提高企业利润，同时也会因为挤占传统零售商渠道的市场占有率而遭到零售商的抵制，引发渠道冲突，比如LEVIS公司曾在引入网上直销渠道后，因没有协调好与零售商的关系而遭到了下游零售商的联合抵制，最终被迫关闭网上直销渠道。不少零售商在直销渠道的压力下实施产品促销策略来与制造商竞争，虽然制造商能够因此接到更多的产品订单，但是双渠道之间的冲突却进一步加剧。引起渠道冲突的一个重要原因是制造商和零售商的决策目标不相容，即供应链未达到协调状态。对于开辟直销渠道的制造商而言，如何协调好双渠道的库存决策是缓解渠道冲突的关键。近年来，供应商管理库存(Vendor Management Inventory, VMI)模式因其在提高供应链运作效率、应对市场突发事件和减弱牛鞭效应等方面具有的优势而受到企业和学术界的重视。VMI是指供应商监控零售商的库存水平，并承担补货的任务，确保达到一定的库存周转目标和顾客服务水平，这种供应链运作模式为协调双渠道供应链中存在的渠道冲突提供了新的思路。本文基于这种问题背景，考虑零售商的促销努力，研究制造商如何在VMI模式下协调供应链成员的库存、促销与定价决策，来缓解直销渠道开辟带来的渠道冲突。在VMI模式下，制造商统一管理双渠道的库存。

针对双渠道供应链的竞争与协调问题，众多学者通过设计契约的方式进行了深入研究。Qin Geng和Mallik[1]在零售商强势并有产能约束的双渠道供应链中，设计了转移支付和逆向收益共享的组合契约实现了双渠道的协调。Chiang[2]在允许缺货的情况下，研究了双渠道供应链的库存竞争与协调问题，设计了收益共享和库存持有成本分担的组合契约使双渠道供应链达到协调状态。Cai Gangshu等[3]分别在双渠道价格一致和不一致情况，研究了价格折扣契约对双渠道利润的影响，结论是使双渠道定价一致或实施价格折扣契约可以缓解渠道冲突。Xu Guangye等[4]在风险规避型双渠道供应链中，使用均值—方差的方法度量风险，提出了两方收益共享契约使双渠道供应链实现了协调。申成然等[5]针对比价行为下部分消费者优先在网络渠道购买产品的现象，研究了双渠道供应链的定价和协调问题，并设计了特许经营和收益共享的混合契约实现了双渠道供应链的完美协调。赵礼强等[6]为了解决混合双渠道的冲突和协调，设计了批发价加电子渠道合同使双渠道供应链达到协调，通过改进的收益共享契约实现了供应链各成员利润的帕累托改进。因为电子商务环境下的促销活动是商家提高产品需求的重要手段之一，所以不少学者在研究了考虑促销努力的双渠道供应链协调问题。Tsay和Agraw[7]认为网络直销渠道和传统零售商渠道在促销上都有外部性，但零售商促销具有成本优势。陈树桢等[8]考虑了零售商促销对传统渠道需求的影响，制造商通过给予零售商激励补偿缓解渠道冲突并激励零售商增大促销投入。禹爱民等[9]在随机需求和联合促销下研究双渠道供应链协调，发现回购契约能给供应链成员带来好处但不能协调供应链，这与Cachon[10]的结论类似。但上述文献均从契约的角度协调双渠道供应链的上下游企业，未能从改变双渠道供应链运作模式的角度研究协调问题，比如研究VMI模式下，双渠道供应链的协调问题。

传统的库存管理模式下，制造商和零售商拥有和控制各自的库存，不同的库存控制策略增加了协调库存决策的难度。VMI模式下，制造商统一制定供应链的库存决策，为库存决策的协调带来了便利条件。在已有的关于VMI的研究中，如何在VMI模式下协调供应链各成员的决策是众多研究者关注的热点问题。Wong等[11]在市场需求与价格相关情况下，探讨了由单一供应商多个竞争的销售商组成的两级VMI供应链的协调问题，并证实销量回扣契约能够实现供应链协调。李新然等[12]在促销努力影响生产需求且生产不确定的VMI供应链中设计了销售回扣和回购相结合的组合契约，研究发现该组合契约能够促使零售商增加促销努力和订货量，供应商增加计划生产量，从而提高供应链的整体的利润。在李欣然等[13]，他们还研究了VMI模式下，考虑促销的季节性产品供应链的协调，发现引入滞销产品补贴的销售回扣契约后，VMI供应链的总收益得到了大幅度提高。刘鹏飞[14]研究了产品需求依赖于零售商促销努力的情况下，对Nash静态博弈下的VMI供应链，提出采用零售商承担供应商部分滞销成本，供应商分担零售商部分促销成本的协调方法，实现了VMI供应链的协调。Yu Yugang[15]在由原材料供应商、单制造商和多零售商的VMI供应链中建立了制造商和零售商的Stackelberg博弈模型，并考虑了促销努力对需求的影响，给出了制造商最优的补货和发货策略。但上述文献均未将VMI模式应用到双渠道供应链中，并进一步探讨需求受促销努力影响下的供应链协调问题。

本文基于上述文献的研究成果，研究由单制造商和多零售商组成的双渠道供应链中的协调问题，其中零售商对产品进行促销，强势的制造商开辟了网上直销渠道并主导实施了VMI策略。本文重点参考Yu Yugang等[15]的研究方法，构建制造商主导的Stackelberg博弈模型，探究制造商协调直销渠道和零售商渠道的库存、定价和促销策略，并从制造商的角度出发，研究如何通过联合促销契约协调供应链。与Yu Yugang等[15]不同的是，本文利用了联合促销契约协调制造商和零售商，并考虑制造商开辟网上销售渠道的情形。

2 联合促销下双渠道的库存协调模型

2.1 问题描述与假设

研究由一个制造商和多个零售商构成的供应链，制造商面对多个零售商实施VMI，负责对多个零售商的供货系统进行检查和补充。这种结构的VMI供应链多出现在制造商是一个比较大的产品制造商的情况下，要求制造商具有相当的规模和实力，完全能够承担起管理VMI的责任。例如，美国的宝洁公司就发起并主导了对国内大型零售商的VMI管理模式的实施。制造商在传统零售商销售渠道的基础上进一步开辟了网上销售渠道，通过双渠道将生产的产品销售出去。在VMI模式下，制造商替各零售商制定订货策略，零售商只有在产品销售出去时，才向制造商支付相应产品的成本，即零售商处的库存为寄售库存。零售商销售渠道和网上渠道的需求均由寄售库存满足。表1是模型中用到的符号与释义。

假设多个零售商存在区域隔离，处于不同的市场，不存在零售商之间库存的转移，也不存在不同区域消费者需求的转移。区域i内只有一个零售商i，该区域的市场需求分为两个部分，即网上渠道需求doi(pi,po,ei)与零售商渠道需求dri(pi,po,ei)。考虑零售商促销时，网上渠道需求和零售商渠道需求的计算公式为：

dsi(pi,po,ei)=DOi(pi,po)+υei=αs[θ(1-βpo)-η(po-pi)]+υei

(1)

表1 模型符号与释义

dri(pi,po,ei)=DRi(pi,po,ei)+(1-υ)ei=αr(1-βpi)+αs[(1-θ)(1-βpi)+η(po-pi)]+(1-υ)ei

(2)

其中，αr，αs分别表示忠于零售商和忠于制造商的销售市场大小；(1-θ)表示忠于制造商的消费者中，会通过零售商渠道购买产品的消费者的比例；η(po-pi)表示双渠道价格不同时，忠于制造商且愿意通过网上渠道购买产品的消费者中，会转向零售商渠道购买产品的消费者的数量，η(po-pi)为负表示一定的需求从零售商渠道转向网上渠道。在公式(1)和公式(2)中，vei和(1-v)ei分别表示因零售商促销而导致的网上直销渠道和零售商渠道需求的增加量。因为现实生活中往往存在这样一种现象，零售商的促销活动使更多的消费者有了购买产品的需求，但部分消费者可能选择网上直销渠道购买产品，因此促销带来的部分需求vei由网络渠道满足，即本文的模型中考虑了双渠道之间存在的搭便车效应。

零售商对产品进行促销，促销的成本由制造商和零售商共同承担，即采用联合促销的方式协调整个供应链的上下游。制造商承担促销成本的比例ω，由制造商和零售商的谈判能力决定。促销成本f(e)的计算公式为：

(3)

本文重点分析制造商和零售商的库存和定价策略，模型中的假设如下：

①制造商和零售商在就库存和定价决策博弈的过程中，分别扮演领导者和追随者的角色，即制造商处于强势地位；

②产品在零售商渠道的缺货完全延迟订购，由下一期补货满足，而网上销售渠道不允许缺货；

③VMI模式下，制造商和零售商的信息是完全共享的。在决策过程中，制造商和零售商均持风险中性态度。

2.2 模型的建立

制造商和零售商就库存和定价决策的博弈符合Stackelberg博弈模型。制造商和零售商的决策目标均为企业利润的最大化。下面给出制造商对寄售库存的补货策略和寄售库存的库存水平的变化，然后求得零售商和制造商在销售周期内的利润，最后构造制造商和零售商之间的博弈模型。

VMI模式下，制造商将产品配送至区域i的寄售库存IFRCi(InventoryforRetailerChannel，IFRC)和寄售库存IFOCi(InventoryforOnlineChannel，IFOC)。寄售库存IFRCi用于满足区域i中零售商渠道的需求，库存水平的变化如图1所示；寄售库存IFOCi用于满足区域i中网上销售渠道的需求，库存水平的变化如图2所示。零售商渠道缺货后，双渠道的需求都会发生变化，原因有两点：一是零售商渠道缺货，一部分需求会从零售商渠道转向网上渠道，根据上文对双渠道需求公式的解释，从零售商渠道转向网上渠道的需求为αsη(po-pi)；二是零售商在缺货时会停止产品的促销活动。因此，双渠道的需求可分为两个阶段，计算公式如下：

dri(pi,po,ei)=

doi(pi,po,ei)=

由此可得，零售商销售渠道和网上销售渠道单位时间内的平均需求dri′(pi,po,ei)和doi′(pi,po,ei)分别为：

dri′(pi,po,ei)=DRi+(1-υ)(1-bi)ei-αsηbi(po-pi)

doi′(pi,po,ei)=DOi+υ(1-bi)ei+αsηbi(po-pi)

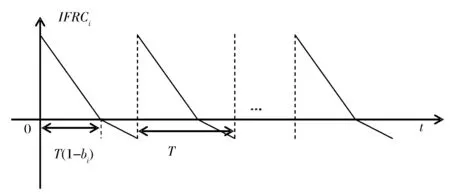
图1 寄售库存IFRCi的库存水平变

图2 寄售库存IFOCi的库存水平变化

1)零售商的利润

零售商i的决策变量为促销量ei以及产品的销售单价pi。零售商i的成本包括产品的批发成本和促销成本。VMI模式下，制造商管理寄售库存IFRCi，决定订货量以及订货周期，由库存所引起的缺货成本，持有成本以及订货成本均由制造商承担而不出现零售商的成本中。因此零售商i的利润为：

∏i(pi,ei)=(pi-cp)[Dri+(1-υ)(1-bi)ei+αsηbi(po-pi)]-(1-ω)f((1-bri)ei)

(4)

2)制造商的利润

(5)

制造商的间接总成本包括：部分促销成本，VMI模式下支付给零售商i的补偿成本CCi以及产品的库存总费用(TIC)，由公式(6)计算：

(6)

补偿成本CCi包括寄售库存IFRCi的订货成本、库存持有成本和缺货成本等。补偿成本CCi由公式(7)计算：

(7)

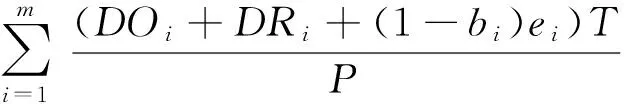
(8)

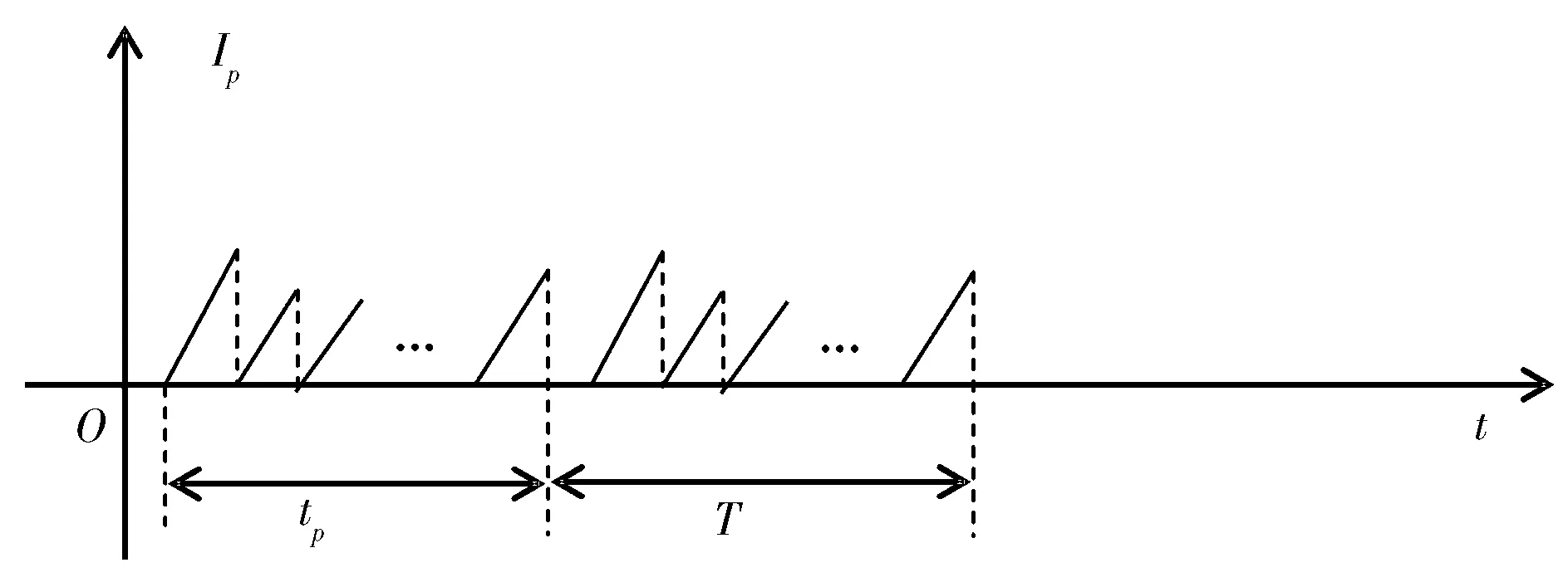
图3 产成品的库存水平变化

至此可得出制造商的利润为：

(9)

3)Stackelberg博弈模型

建立制造商和零售商之间的Stackelberg主从博弈模型如下。

(1)制造商的决策模型

max ∏M(b1,b2,…,bm,T,cp,po)

(10)

s.t.

(11)

0≤bi≤1,i=1,2,…,m

(12)

cp,T>0

(13)

其中，约束(11)保证了制造商可以生产出足够多的产品满足双渠道的需求，约束(12)和(13)分别对零售商i的缺货时间比例、产品的批发价和产品的补货周期做出了限制。

(2)零售商i的决策模型

max ∏i(pi,ei)

(14)

s.t.pi,ei≥0，i=1,2,…,m

(15)

其中，约束(15)对零售商的i的价格和促销量做出了限制。

2.3 模型的求解

1)零售商的决策

对于上述Stackelberg博弈模型，采取逆推的求解方法，即首先求出零售商决策对制造商决策的反应函数，然后分析制造商的最优决策。求解零售商反应函数时，假定制造商的决策变量已知。零售商i的决策变量有促销量ei和销售单价pi。由公式(16)可求出零售商i的利润对促销量ei的一阶段偏导数：

(16)

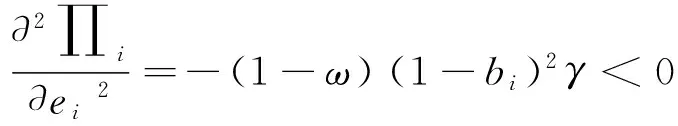
(17)

由公式(4)可得零售商i的利润对销售单价pi的一阶段偏导数与二阶偏导数：

(18)

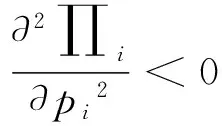
2)制造商的决策

制造商的决策变量为：产品的批发价格cp、零售商的补货周期T、整个销售周期T内零售商i的缺货时间所占的比例bi和网上渠道的销售价格po。将零售商的最优决策带入公式(9)并求出制造商的利润函数对bi的一阶偏导数和二阶偏导数：

-(DRi-ηαs(po-pi))biTLi

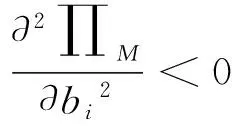
(19)

Yu Yugang[15]在制造商未开辟网上销售渠道的情况下，求出的零售商缺货时间比例为：

显然，制造商开辟网上销售渠道并实施联合促销策略后，零售商缺货时间比例变大，这表明双渠道的开辟带来了渠道冲突，制造商以增加零售商渠道缺货成本的代价争夺了零售商渠道的部分需求。

将(19)式带入公式(9)并求出制造商的利润函数对订货周期T的一阶偏导数和二阶偏导数：

(20)

显然，令(20)式为零，可以求出制造商的最优补货周期T*：

(21)

其中：

基于以上分析，制造商的决策模型可以简化为：

s.t.

min{p1,p2,…,pm}≥ps

这是一个不等式约束下的极值问题，将该模型进一步转化为：

s.t.

该模型的Kuhn-Tucker条件为：

(22)

(23)

μ2(po-min{p1,p2,…,pm})=0

(24)

(25)

根据(22)～(25)式可解出最优批发价格cp*和最优网上渠道定价po*。

3 算例分析

为了进一步分析联合促销对制造商和零售商决策的影响并对模型主要参数进行灵敏度分析，给出一个算例。表2是模型中主要参数的取值。

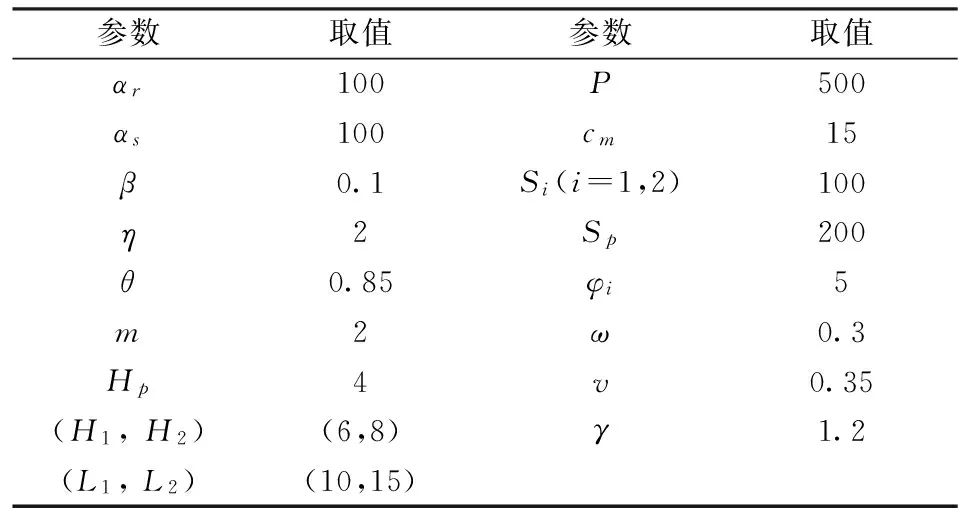
表2 模型主要参数的取值

本算例设定双渠道VMI供应链由1个制造商和2个零售商组成，根据上文介绍的求解方法，可以求解出制造商和2个零售商的决策变量，表3为计算结果。

表3 制造商和零售商的决策变量

从表3中可以看出，零售商1的缺货时间比例大于零售商2。VMI模式下制造商负责为两个零售商补货，零售商的缺货时间比例是制造商的决策变量。由表3可知，零售商1的促销量为34.1，大于零售商2的促销量20.4，因此制造商需要在零售商1的销售渠道上承担更多的促销成本，此时制造商也可以通过搭便车效应从零售商1处得到更多的网上渠道销售需求，带来更多的收入，从促销的角度看，如果通过搭便车效应为制造商带来的收入大于所需承担的促销成本，那么制造商会缩短零售商的缺货时间。由表2可知，寄售库存IFRC1的库存持有成本和缺货成本均低于寄售库存IFRC2，因此从库存管理成本的角度看，制造商会降低零售商2的缺货时间比例。而最终两零售商的缺货时间比例是上述促销成本、搭便车效应以及库存管理成本三个因素的综合效果。由此看来，零售商的促销活动和双渠道之间存在的搭便车效应是供应链成员决策时需要考虑的重要因素，下面仍以表2中的数据为基础，对制造商承担促销成本的比例ω和搭便车效应中的参数v进行灵敏度分析。

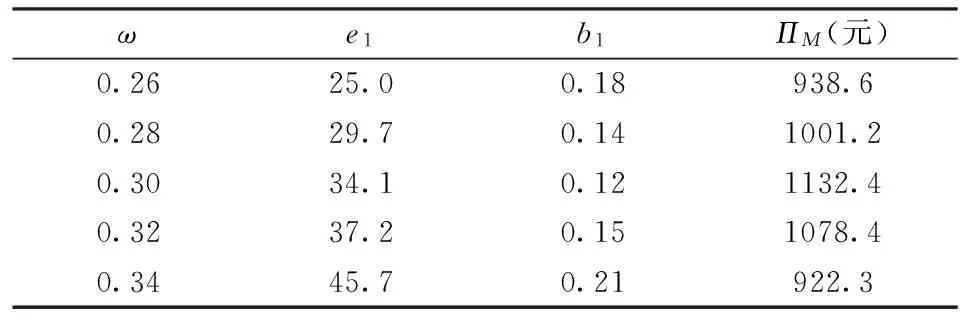
表4 制造商承担促销成本的比例ω的灵敏度分析

从表4来看，制造商承担促销成本的比例ω越高，零售商1的促销量越高，这与公式(17)相符。但零售商1的缺货时间比例呈现出先变小后变大的趋势，制造商的利润也呈现出先增加后减少的趋势，这是因为随着ω的提高，零售商促销量不断增加，搭便车效应为制造商带来的更多网上渠道的销售需求和收入，同时也增加了所需承担的促销成本，促销成本函数f(e) 满足f(e)′>0，f(e)″>0，即促销量越大，促销成本越大，继续提高1单位促销量所需的成本越高，而提高1单位促销量为制造商带来的收入是不变的，因此存在最优的促销成本承担比例ω使得制造商利润最大，当促销量的增加所带来的收入无法抵消所需承担的促销成本时，制造商就会选择让零售商缺货。

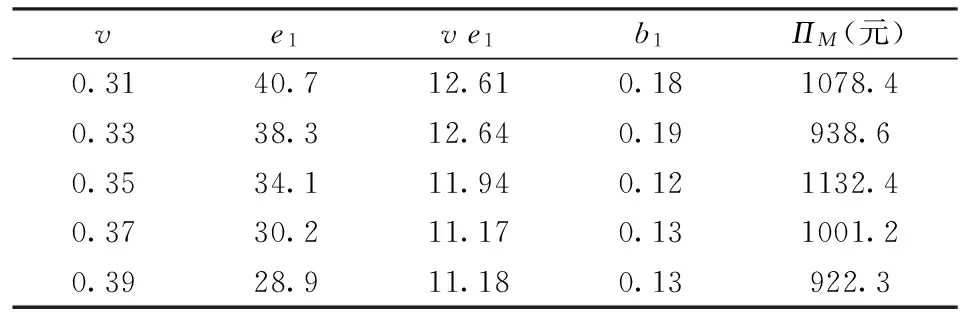
表5 搭便车效应参数v的灵敏度分析

由表5可知随着v的增加，即制造商通过搭便车效应获得的促销量比例增加，零售商的促销量逐渐减少，这与公式(17)相符，不过零售商的缺货时间比例，制造商由搭便车效应带来的需求的增加量ve1和利润并未呈现出有规律的变化。

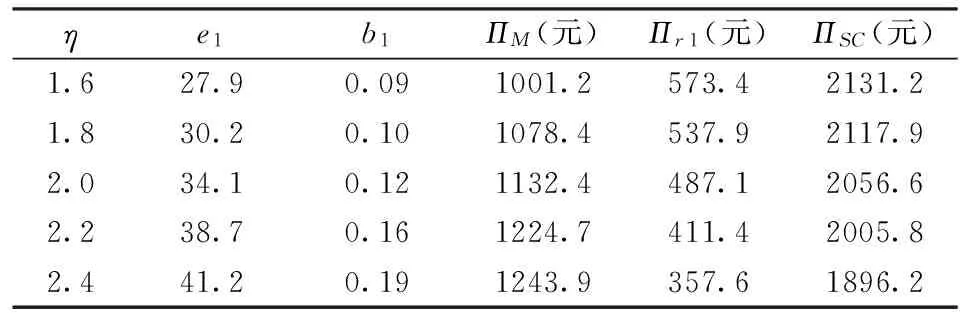
表6 参数η的灵敏度分析

最后，对双渠道需求函数中的参数η进行灵敏度分析。根据本文对η(po-pi)和αsη(po-pi)的解释可知，η的大小决定了双渠道需求的稳定程度，η越大，由于价格波动或者一个销售渠道缺货所导致的双渠道需求的转化程度就越大，即双渠道需求就越不稳定。从表6来看，η越大，缺货时间比例越大，制造商的利润越大。这是因为：①当η越大时，由零售商渠道缺货而转向网上渠道的需求就越多；②零售商渠道需求减小导致单位时间所累积的缺货量降低，即缺货成本不会因为η的增大而快速增加，所以制造商会提高零售商缺货时间比例促使自身利润增加。另外，从制造商、零售商和供应链整体的利润来看，η越大，即双渠道的需求越不稳定，对制造商越有利，但对零售商和供应链整体不利。

4 结语

本文以混合双渠道供应链为背景，在零售商对产品进行促销和制造商主导实施VMI策略的条件下，研究制造商和零售商的库存、促销和定价决策，建立了制造商和零售商的Stackelberg博弈模型，其中制造商通过承担部分零售商的促销成本来协调供应链的上下游。研究得出以下结论：

(1)制造商开辟了网上销售渠道后，零售商的缺货时间比例会增加。这说明网上直销渠道的开辟加剧了制造商和零售商之间的渠道冲突，零售商的服务水平(订单满足率)会因此下降；

(2)制造商承担促销成本比例的提高将促使零售商提升促销力度，但承担促销成本的比例过高会损害制造商本身的利益，因为随着承担促销成本比例的提升，搭便车效应给制造商带来的收益将无法抵消快速增长的促销成本；

(3)零售商的促销努力带来的需求增加量会有部分转至网上直销渠道销售，这种搭便车的现象会打击零售商促销的积极性，即搭便车效应越强，零售商的促销努力越弱；

(4)双渠道需求越不稳定，即价格波动和渠道缺货导致的双渠道需求的转化程度越大，则制造商的利润越高。搭便车效应的强弱以及双渠道之间需求的稳定性与实际的市场销售环境及消费者的消费心理有关，结论(3)和(4)说明双渠道本身的结构和特性也是企业决策需要考虑的重要因素。

在上游企业开辟网上直销渠道并实施VMI的供应链中，上述结论可以为供应链成员制定库存、定价和促销决策提供指导。在实施VMI的供应链中，制造商拥有寄售库存的决策权，可能会隐匿相关的库存信息，这将破坏供应链协调。因此，如何协调信息不对称条件下的双渠道VMI供应链将是进一步的研究方向。

[1] Qin Geng, Mallik S. Inventory competition and allocation in a multi-channel distribution system[J]. European Journal of Operation Research, 2007,182(2):704-729.

[2] Chiang W Y K. Product availability in competitive and cooperative dual-channel distribution with stock-out based substitution[J]. European Journal of Operational Research,2010,200(1):111-126.

[3] Cai Gangshu, Zhang Z G, Zhang M. Game theoretical perspective on dual-channel supply chain competition with price discounts and pricing schemes[J]. International Journal of Production Economics, 2009, 117(1):80-96.

[4] Xu Guangye, Dan Bin, Zhang Xumei,et al. Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract[J]. International Journal of Production Economics,2014,147:171-179.

[5] 申成然,熊中楷,晏伟.网络比价行为下双渠道定价及协调策略研究[J].中国管理科学,2014,22(1):85-93.

[6] 赵礼强,徐家旺.基于电子商场的供应链双渠道冲突与协调的契约设计[J].中国管理科学,2014,22(5):61-68.

[7] Tasy A，Agrawal N. Channel conflict and coordination in the e-commerce age[J]. Production and Operations Management,2004,13(1):93-110.

[8] 陈树桢，熊中楷，梁喜．补偿激励下双渠道供应链协调的合同设计[J]．中国管理科学,2009,17(1):64-75．

[9] 禹爱民, 刘丽文. 随机需求和联合促销下双渠道供应链的竞争与协调[J].管理工程学报,2012, 26(1):151-155.

[10] Cachon G. Supply chain coordination with contracts in supply chain management: Design，coordination and operations[M]//DeKok A G, Graves S C. Handbooks in Operations Research and Management Science, Amsterdam, The Netherlands:Elsevier B V,2003:229-341.

[11] Wong W K, Qi J, Leung S Y S. Coordinating supply chains with sales rebate contracts and vendor-managed inventory[J].International Journal of Production Economics,2009,120(1):151-161.

[12] 李欣然,黎高,牟宗玉.促销努力和生产不确定下的VMI契约研究[J].科研管理,2012,33(4):131-138.

[13] 李欣然,牟宗玉,黎高.VMI模式下考虑促销努力的销售回扣契约模型研究 [J].中国管理科学,2012,20(4):88-94.

[14] 刘鹏飞.需求以来零售商努力水平的VMI协调[J].系统工程学报,2012,27(5):679-684.

[15] Yu Yugang, Huang G Q, Liang Liang. Stackelberg game-theoretic model for optimizing advertising, pricing and inventory policies in vendor managed inventory (VMI) production supply chains[J]. Computers & Industrial Engineering, 2009,57(1):368-382.

Competing and Coordination Strategies for Dual Channel under VMI Supply Chain with Cooperative Promotion

WANG Dao-ping，ZHANG Bo-qing，LI Xiao-yan

(Donlinks School of Economics and Management, University of Science andTechnology Beijing, Beijing, 100083)

With the development of E-commerce, more and more manufactures have established a online distribution channel while keeping traditional retail channel, thus having dual channel to distribute products. Online distribution channel helps manufactures widen the market scope and decrease the operation cost. But it also hurts the retailers profit, thus being subject to retailers' resistances and lead to channel conflict. The appearance of VMI pattern inspires research into competing and coordination strategies for dual channel under VMI supply chain. However previous researches didn't focus on these supply chain. Based on a two-stage VMI supply chain including a manufacturer and multiple retailers, a model of Stackelberg game between a manufacturer and retailers is developed in this paper, considering cooperative promotion in which supply chain can be coordinated and online distribution channel established by manufacturer. The decision variables of manufacture include the quantity of retailers' order, the cycle of retailers' order and price of product which is sold via online channel. Retailers need to determine price of product sold via traditional retailer channel and promotion quantity. It is found that fraction of backlogging rate for retailers become bigger compared with a supply chain without online distribution channel. Furthermore，the increase of cooperative promotion ratio and the fade of free riding' effect leads to higher quantity of promotion; the increase of demand transformation between dual channel leads to higher profit of manufacturer and lower profit of retailers and the whole supply chain. Finally，a numerical example is given to illustrate the theoretical results of the proposed model and conduct sensitivity analysis on parameters of the proposed model.

cooperative promotion; dual channel supply chain; vendor management inventory; coordination of supply chain

1003-207(2016)03-0052-09

10.16381/j.cnki.issn1003-207x.2016.03.007

2014-07-31；

2015-04-07

国家自然科学基金资助项目(71172169)

简介：王道平(1964-)，男(汉族)，北京人，北京科技大学东凌经济管理学院，教授，博士生导师，研究方向：供应链管理、知识管理等，E-mail:dpwang@ustb.edu.cn.

F270

A