固定-导向柔顺杆件6R伪刚体模型

刘 凯 曹 毅, 2, 3 葛姝翌

1.江南大学，无锡，2141222.上海交通大学系统控制与信息处理教育部重点实验室，上海，2002403.哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨，150080



固定-导向柔顺杆件6R伪刚体模型

刘 凯1曹 毅1, 2, 3葛姝翌1

1.江南大学，无锡，2141222.上海交通大学系统控制与信息处理教育部重点实验室，上海，2002403.哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨，150080

为提高固定-导向型伪刚体模型的计算精度，基于伪刚体模型的原理提出了一种固定-导向6R伪刚体模型。建立了该模型的运动学方程，并根据逆运动学分析方法及优化算法求解了模型的4个最优特征半径系数和3个扭簧刚度系数。通过数值算例模拟固定-导向6R伪刚体模型的末端动作路径，并将其与固定-导向2R伪刚体模型及柔顺杆件的末端路径进行对比。结果表明，固定-导向6R伪刚体模型能够更加精确地模拟相应柔顺杆件的末端动作过程，且其相对误差几乎为0。最后，通过ANSYS有限元分析实例验证了该模型在实际计算中的精确性。

伪刚体模型；固定-导向柔顺杆件；优化算法；有限元分析

0 引言

柔顺机构是一种利用机构杆件自身柔性变形来实现运动和力传递或转换的新型机构[1]。对柔顺机构的研究主要包括柔顺机构的设计、优化及其高效分析模型的建立。Yoo[2]等、张宪民[3]结合拓扑学对柔顺机构进行了设计、分析。陈贵敏等[4]基于伪刚体建模方法，给出了一种有效的平面柔顺机构自由度计算方法。秦振等[5]基于有限元法对以柔性框架为主体的步行机进行了仿真分析。Friedrich等[6]建立了柔顺机构圆形柔性铰链的非线性模型。王伟华等[7]、Ahuett-Garza等[8]分别对大变形情况下的柔顺杆件与柔性铰链进行了研究。

由于柔顺机构常常出现几何非线性大变形，因此分析过程纷繁复杂。为了简化柔顺杆件的计算过程，Howwell等[9-10]率先提出了悬臂梁模式和固定-导向模式下的最简伪刚体模型，并利用数理统计的方法求得相关特征参数。基于此模型，Dado[11]建立了力载荷作用下大变形梁的变参数伪刚体模型。另外，冯忠磊等[12]、Su[13-14]分别提出了悬臂梁模式下2R和3R伪刚体模型，提高了模型的分析精度。余跃庆等[15-16]在伪刚体模型中引入了移动副，建立了悬臂梁模式下PR伪刚体模型，充分考虑了杆件的轴向变形。Wang等[17]针对分析过程更为复杂的波纹悬臂梁建立了伪刚体模型并用仿真验证了其正确性。综上所述，国内外学者对柔顺机构的研究已经取得了大量成果，但对于力载荷作用下的固定-导向柔顺杆件的变形分析，仅有Howwell提出的固定-导向2R伪刚体模型能简化其计算过程，但是此模型仍存在以下问题：①模型的计算精度有限；②无法模拟固定-导向柔顺杆件的中点处转角。

针对上述问题，本文基于伪刚体模型的原理提出了一种固定-导向6R伪刚体模型，并通过优化算法确定了该模型的4个半径特征参数和3个扭簧刚度系数。之后通过数值算例模拟该模型的末端运动轨迹，并将其与固定-导向柔顺杆件和固定-导向2R伪刚体模型的末端轨迹相比较，证明了该模型的优越性。最后用ANSYS实例验证了该模型在实际计算中的精确性。

1 固定-导向6R伪刚体模型

末端受力载荷作用的固定-导向柔顺杆件如图1所示，该杆的一端被固定，另一端被“导向”，即使该杆件的末端仅可实现平移而不能转动。由于末端要保持一个固定角度，因此末端必有相应的力矩(图1中的M0)，故所得的杆件变形关于中心线反对称。

图1 固定-导向柔顺杆件

如图1所示，θ0为杆件中点处的转角；φ为力F与x轴的夹角；(a,b)为杆件末端的坐标；末端载荷在垂直方向上的分力为Fy，轴向分力Fx=nFy=-Fycotφ，其中，n>0代表对未变形杆件产生压力，总力F为

(1)

固定-导向柔顺杆件末端的量纲一坐标分量为

(2)

(3)

λ=sinθ0-ncosθ0

式中，α为量纲一载荷参数；L为杆件长度。

伪刚体模型用具有等效力-变形关系的刚体构件来模拟柔顺部件的变形，以实现刚体静力学理论对柔顺机构的分析。综合考虑图2所示的固定-导向2R伪刚体模型的计算精度及结构，本文提出了固定-导向6R伪刚体模型，如图3所示。固定-导向6R伪刚体模型由7个刚性杆件、6个转动副和6个扭簧(代表柔顺杆件的抗弯能力)组成。γi(i=0, 1, 2, 3)为模型段的特征半径系数，满足2γ0+2γ1+2γ2+γ3=1；Kc(c=1, 2, 3)为扭簧常数，对应扭簧刚度系数Kθc；θc为伪刚体角；柔顺杆件的中点处转角θ0=θ1+θ2+θ3；Qw为模型末端位置；l为杆件的总长，其与特征半径系数的乘积即为各段刚性杆件的长度。下文将对4个半径特征系数和3个扭簧刚度系数进行求解。

图2 固定-导向2R伪刚体模型

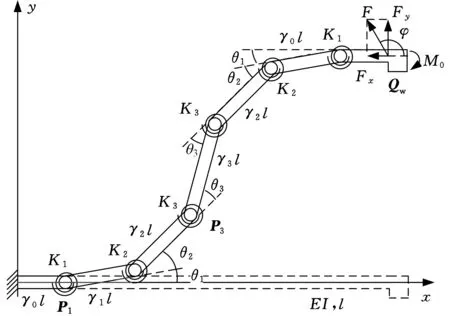
图3 固定-导向6R伪刚体模型

2 模型系数求解

2.1 运动学分析

首先对固定-导向6R伪刚体模型进行运动分析和受力分析，建立其运动学方程。由图3可得模型末端的量纲一坐标：

Qw=(Qwx,Qwy)=(a/l,b/l)=

(2γ0+2γ1c1+2γ2c12+γ3c123，2γ1s1+2γ2s12+γ3s123)

(4)

c1=cosθ1，s1=sinθ1，c12=cos(θ1+θ2)，

s12=sin(θ1+θ2)，c123=cos(θ1+θ2+θ3)，

s123=sin(θ1+θ2+θ3)

在已知模型末端点位置Qw和中点处转角θ0的情况下，根据逆运动学分析可求出固定-导向6R伪刚体模型的伪刚体角θ1、θ2和θ3：

(5)

(6)

θ3=θ0-θ1-θ2

(7)

为了简化计算，引入一个从P1到P3的矢量：

2.2 刚度系数和特征半径系数

固定-导向柔顺杆件的抗弯能力可以用量纲一的扭簧刚度系数Kθc来描述。对于给定的固定-导向6R伪刚体模型末端力载荷，模型中转动副处的扭矩为

(8)

式中，Fx=Fcosφ为水平作用力；Fy=Fsinφ为垂直作用力。

扭矩Tc为扭簧常数Kc与伪刚体角θc之间的乘积，即Tc=Kcθc。因此

diag(θ1，θ2，θ3)[K1K2K3]T=J[FxlFyl]T

(9)

扭簧常数Kc与扭簧刚度系数Kθc、几何关系I/l、材料特性E有关：

Kc=KθcEI/l

故式(9)亦可以表示为

(10)

由式(10)可得

(11)

将量纲一的力载荷系数α2=Fl2/(EI)代入式(11)，可得

(12)

模型特征半径系数γi的初始值可通过变形最大允许误差得到。然后，进一步确定既能产生最大参数化极值角θ0max，同时又满足误差限制的γ，其中，误差限制条件为

(13)

(14)

(15)

式中，e为绝对变形误差；e/δe为相对变形误差。

当满足上述条件的γi较多时，取不同的n，选择使各组扭簧系数的差平方之和最小的γi作为固定-导向6R伪刚体模型的特征半径系数，以确保所求解扭簧刚度系数的稳定性，具体的判断条件为

(16)

根据参数约束条件及运动学方程，固定-导向6R伪刚体模型的特征半径系数可用图4所示的流程求得，其中，Δθ0为搜索步长，|(e/δe)max|为最大允许误差。

图4 半径特征系数的计算步骤程序框图

为验证上述算法的正确性，设定相对变形的最大允许误差|(e/δe)max|为0.1%，Δθ0为0.01，n分别取0、±0.5、±1、±1.5、±2、±3、±4、±5，最终求得固定-导向6R伪刚体模型的最优特征半径系数：γ0=0.030, γ1=0.050, γ2=0.245, γ3=0.350。

根据已知的特征半径系数γi，利用式(12)求得在不同力作用角度下的扭簧刚度系数Kθc。进一步研究发现扭簧刚度系数Kθc几乎不随力载荷系数α2的增加而变化，基本维持在一个定值附近，现将这个定值记录并汇总于表1。

根据表1所示数据可知，n不同时，固定-导向6R伪刚体模型的3个扭簧刚度系数都较为稳定，可以用给定范围内的平均值表示；值得指出的是,多数力载荷都在63°<φ<135°，即-0.5

Kθ1=19.409 64，Kθ2=9.148 42， Kθ3=6.977 52

表1 不同力作用角度下的扭簧刚度系数值

3 模型计算精度分析

3.1 模型末端运动轨迹精度分析

为验证固定-导向6R模型末端运动轨迹的精确性，将固定-导向6R伪刚体模型(γ0=0.030,γ1=0.050,γ2=0.245,γ3=0.350,Kθ1=19.409 64,Kθ2=9.148 42,Kθ3=6.977 52)、固定-导向2R伪刚体模型(γ=0.85,Kθ=2.65)及固定-导向柔顺杆件的末端运动轨迹绘制于图5。同时，为了更直观地表达两种模型的末端运动轨迹误差，根据已知的伪刚体模型及固定-导向柔顺杆件的末端位置Qw、Q，联立式(13)～式(15)可求得相对误差e/δe，利用相对误差值绘制得到图6所示的模型末端轨迹误差曲线。

图5 末端运动轨迹对比

图6 两种模型的末端运动轨迹误差

由图5、图6可知，两种模型的末端运动轨迹和基于椭圆积分求解的固定-导向柔顺杆件的末端运动轨迹基本吻合，但固定-导向6R伪刚体模型的轨迹误差几乎始终为0；对于固定-导向2R伪刚体模型，当转角增加到一定值后误差就会快速上升至10%以上。因此，固定-导向6R伪刚体模型的末端轨迹模拟精度更高。

3.2 模型中点处转角精度分析

图7描述了固定-导向柔顺杆件、固定-导向6R伪刚体模型及固定-导向2R伪刚体模型在不同位置的中点处转角。如图7所示，固定-导向6R伪刚体模型和固定-导向柔顺杆件各位置对应的中点处转角几乎完全吻合，而固定-导向2R伪刚体模型的中点处转角与柔顺杆件相比有较大差异。

图7 中点处转角对比

上述研究分析证明了固定-导向6R伪刚体模型的优越性，其完全能够精确模拟固定-导向柔顺杆件的末端运动轨迹及中点处转角。

4 ANSYS仿真验证

为了验证固定-导向6R伪刚体模型在实际计算中的正确性，本文设计了固定-导向柔顺杆件变形分析实例，基于ANSYS建立了该杆件的有限元模型，并将有限元分析结果与该模型的计算结果进行对比。

所设计实例的结构参数如下：杆件长L=50 mm，宽B=5 mm，高h=4 mm。本例中选择强度与弹性模量之比较高的ABS工程塑料(弹性模量E=2.2 GPa，泊松比ν=0.34)作为柔顺杆件的材料。在杆件的一端添加固定约束，另一端添加“导向”约束，同时在“导向”端施加不同作用角度的力载荷。由图8可知，φ=90°，F=100 N时，ANSYS计算的杆件变形量δ1=15.949 mm；联立伪刚体模型的式(4)、式(8)求得杆件的变形量δ2=15.951 mm。选择不同大小的力可以得到表2所示的计算分析结果。

图8 杆件变形图

从表2中可以发现，固定-导向6R伪刚体模型的计算值和有限元分析结果的吻合度较高，最大误差不超过2.5545%；当力作用角度φ分别为63.4°，116.6°，135°时，杆件变形量的两种计算结果

表2 杆件变形有限元仿真值与理论计算值(力作用角为90°)

果如图9～图11所示，仍保持了较高的相似度。φ=63.4°时，最大误差不超过2.4007%；φ=116.6°时，最大误差不超过3.0728%；φ=135°时，最大误差不超过2.8426%。由上述分析可知，固定-导向6R伪刚体模型在实际计算中有较高的精确性，完全可以用于柔顺机构的变形分析。

图9 力作用角为63.4°时杆件变形量随力的变化

图10 力作用角为116.6°时杆件变形量随力的变化

图11 力作用角为135°时杆件变形量随力的变化

5 结论

(1)基于伪刚体模型的原理，本文提出了一种固定-导向6R伪刚体模型，该模型能够精确模拟固定-导向柔顺杆件的末端运动轨迹及中点处转角。

(2) 提出了固定-导向6R为刚体模型各参数的优化算法，并利用该算法求解了γi和Kθc。

(3) 用数值算例证明了固定-导向6R伪刚体模型的优越性。

(4) 通过ANSYS有限元分析实例验证了固定-导向6R伪刚体模型在实例计算中的精确性。

[1] Howell L L．Compliant Mechanisms[M]．New York：John Wiley & Sons，2001．

[2] Yoo K S，Han S Y．Topology Optimum Design of Compliant Mechanisms Using Modified Ant Colony Optimization[J]．Journal of Mechanical Science and Technology，2015，29(8)：3321-3327．

[3] 张宪民．柔顺机构拓扑优化设计[J]．机械工程学报，2003，39(11)：47-51. Zhang Xianmin. Topology Optimization of Compli-ant Mechanisms[J]. Chinese Journal of Mechanical Engineering，2003，39(11)：47-51.

[4] 陈贵敏，李端玲．平面柔顺机构的自由度[J]．机械工程学报，2010，46(13)：48-53． Chen Guimin，Li Duanling．Degree of Freedom of Planar Compliant Mechanisms[J]．Journal of Mechanical Engineering，2010，46(13)：48-53．

[5] 秦振，阎绍泽．压电陶瓷驱动微小型步行机的设计与仿真研究[J]．机械设计与研究，2004，20(4)：14-17． Qin Zhen，Yan Shaoze．Design and Simulation Research of a Miniature Robot Drive by Piezoelectric Actuator[J]. Machine Design and Research，2004，20(4)：14-17．

[6] Friedrich R，Lammering R，Heurich T. Nonlinear Modeling of Compliant Mechanisms Incorporating Circular Flexure Hinges with Finite Beam Elements[J]. Precision Engineering，2015，42：73-79．

[7] 王华伟，余跃庆，苏丽颖，等．柔顺机构动力学建模新方法[J]．机械工程学报，2008，44(10)：96-103． Wang Huawei，Yu Yueqing，Su Liying，et al．New Method for the Dynamic Modeling of Compliant Mechanism[J]. Journal of Mechanical Engineering，2008，44(10)：96-103．

[8] Ahuett-Garza H，Chaides O，Garcia P N，et al．Studies about the Use of Semicircular Beams as Hinges in Large Deflection Panar Compliant Mechanisms[J]. Precision Engineering，2014，38(4)：711-727．

[9] Howell L L，Midha A，Noron T W．Evaluation of Equivalent Spring Stiffness for Use in a Pseudo-rigid-body Model of Large-deflection Compliant Mechanisms[J]．Journal of Mechanical Design，1996，118(1)：126-131．

[10] Howell L L，Midha A. Parametric Deflection Approximations for End-loaded，Large-deflection Beams in Compliant Mechanisms[J]. Journal of Mechanical Design，1995，117(1)：156-165．

[11] Dado M H．Variable Parametric Pseudo-rigid-body Model for Large-deflection Beams with End Loads[J]. International Journal of Non-Linear Mecha-nics，2001，36(7)：1123-1133．

[12] 冯忠磊，余跃庆，王雯静．模拟柔顺机构中柔顺杆件末端特征的2R伪刚体模型[J]．机械工程学报，2011，47(1)：36-42． Feng Zhonglei，Yu Yueqing，Wang Wenjing．2R Pseudo-rigid-body Model of Compliant Mechani-sms with Compliant Links to Simulate Tip Characteristic[J]. Journal of Mechanical Engineering，2011，47(1)：36-42．

[13] Su H J．A Pseudorigid-body 3R Model for Determining Large Deflection of Cantilever Beams Subject to Tip Loads[J]．Journal of Mechanisms and Robotics，2009，1(2)：795-810．

[14] Su H J．A Load Independent Pseudo-rigid-body 3R Model for Determining Large Deflection of Beams in Compliant Mechanisms[C]//ASME 2008 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York：ASME，2008：109-121．

[15] 余跃庆，周鹏．柔顺机构PR伪刚体模型[J]．北京工业大学学报，2013，39(5)：641-647． Yu Yueqing，Zhou Peng．PR Pseudo-rigid-body Model of Compliant Mechanisms[J]．Journal of Beijing University of Technology，2013，39(5)：641-647．

[16] 余跃庆，徐齐平，周鹏．复合载荷作用下柔顺机构的PR伪刚体新模型[J]．机械工程学报，2013，49(15)：9-14． Yu Yueqing，Xu Qiping，Zhou Peng．New PR Pseudo-rigid-body Model of Compliant Mechanisms Subject to Combined Loads[J]．Journal of Mechanical Enginee-ring，2013，49(15)：9-14．[17] Wang N，Liang X，Zhang X．Pseudo-rigid-body Model for Corrugated Cantilever Beam Used in Compliant Mechanisms[J]. Chinese Journal of Mechanical Eng-ineering，2014，27(1)：122-129．

(编辑 张 洋)

6R PRBM of Fixed-guided Compliant Links

Liu Kai1Cao Yi1, 2, 3Ge Shuyi1

1.Jiangnan University, Wuxi, Jiangsu，214122 2.Key Laboratory of System Control and Information Processing, the Ministry of Education,Shanghai Jiao Tong University, Shanghai, 200240 3.State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin, 150080

Based on the principles of PRBM, a new fixed-guided 6R PRBM was presented to improve the calculation accuracy for the fixed-guided compliant links firstly. Secondly, the kinematics equation of the model was set up, and the optimal characteristic radius coefficients and the spring stiffness coefficients were acquired using the optimization algorithm and inverse kinematical analysis. In order to validate the calculation accuracy of the fixed-guided 6R PRBM, numerical examples were demonstrated by comparing the tip locus of the fixed-guided 6R PRBM with that of the fixed-guided 2R PRBM. Further research shows that the fixed-guided 6R PRBM may actually simulate the tip locus of the compliant links and the relative error is almost equal to zero. Finally, the accuracy of the model in actual calculation was verified by finite element analysis and engineering examples.

pseudo-rigid-body model (PRBM); fixed-guided compliant link; optimization algorithm; finite element analysis

2015-12-30

国家自然科学基金资助项目(50905075)；江苏省“六大人才高峰”资助项目(ZBZZ-012)；机器人技术与系统国家重点实验室开放基金资助项目(SKLRS-2016-KF-06)；系统控制与信息处理教育部重点实验室开放基金资助项目(scip-201506)

TH112

10.3969/j.issn.1004-132X.2016.21.014

刘 凯，男，1991年生。江南大学机械工程学院硕士研究生。主要研究方向为柔顺机构学。曹 毅，男，1974年生。江南大学机械工程学院副教授,系统控制与信息处理教育部重点实验室访问学者，机械人技术与系统国家重点实验室访问学者。葛姝翌，女，1992年生。江南大学机械工程学院硕士研究生。