电液驱动3-UPS/S并联稳定平台的动力学参数辨识

郭 菲 李永泉 李玉昆 张 宇 张立杰

1.燕山大学河北省重型机械流体动力传输与控制实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，0660043.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004



电液驱动3-UPS/S并联稳定平台的动力学参数辨识

郭 菲1,2李永泉2,3李玉昆2,3张 宇1,2张立杰1,2

1.燕山大学河北省重型机械流体动力传输与控制实验室，秦皇岛，0660042.燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，0660043.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

以电液驱动并联稳定平台为研究对象，对平台惯性参数和驱动关节液压缸摩擦参数进行了基于实验的辨识研究。利用关键点旋量等效原则和虚功原理构建了平台惯性参数辨识模型，以五次多项式改进的傅里叶级数构造了激励轨迹，并进行了优化；基于液压缸摩擦力模型，分离出模型中固有的摩擦参数，建立了摩擦参数辨识模型，并规划了辨识轨迹。通过辨识实验得到了惯性参数及摩擦参数的辨识结果，利用任意轨迹实验对结果进行了验证。

参数辨识；并联机器人；激励轨迹；动力学

0 引言

以并联机器人为基础结构的稳定平台具有可承受重载、响应快、稳定精度高等优点，在测量跟踪及现代武器装备中有着越来越多的应用[1]。为了实现平台高速、高精度的稳定跟踪，多采取动力学控制方法[2]。动力学模型是研究动力学控制方法的基础，模型的准确度直接影响了控制的精度，因此对动力学参数进行辨识是至关重要的。

基于实验的辨识方法是近年应用较多的动力学参数辨识方法[2-5]。Díaz-Rodríguez等[6]对3-RPS和3-PRS并联机器人进行了参数辨识，并提出了动力学参数的物理可行性原则来简化待辨识参数，但是参数的物理可行性判别尚有待研究。Chen等[7]对六自由度电液驱动运动模拟器进行了参数辨识，在其关节空间和操作空间分别优化得到了激励轨迹，提出并验证了采用操作空间激励轨迹可降低辨识的复杂度，但是在优化激励轨迹时没有考虑运动学边界约束，故在实验中易引起机器人的颤振，从而造成测量的不准确。吴军[8]利用两步辨识法对三自由度冗余并联机床进行了参数辨识，并通过适当轨迹规划来分离摩擦因数，进而单独辨识出与惯性矩阵有关的动力学参数。黄田等[9]提出了分层递阶的动力学参数辨识方法，通过设计针对性的辨识轨迹，避免了摩擦的影响，得到了A3主轴头惯性参数的辨识结果。从参数对动力学模型准确度的影响上来看，除惯性参数外，关节摩擦参数同样不可忽视。因此，为获得更加准确的机器人系统动力学模型，应对惯性参数及摩擦参数进行全面辨识。

本文以3-UPS/S并联稳定平台为研究对象。首先，建立各运动构件动力学模型及驱动关节摩擦模型分别关于惯性参数及摩擦参数的线性化形式，得到独立的待辨识基本动力学参数。然后，设计不同辨识策略，优化惯性参数辨识的激励轨迹[10-11]及摩擦参数辨识的轨迹。最后，搭建实验平台进行辨识及验证，得到辨识结果并验证了其可靠性。

1 动力学模型

如图1所示，电液驱动3-UPS/S并联型稳定平台由动平台、定平台、3个UPS主动支链和中央立柱组成。主动支链中，液压缸作为移动副(P)实现驱动运动，并通过虎克铰(U)连接到定平台，通过球铰(S)连接到动平台；中央立柱固定于定平台，通过中央球铰(S)连接到动平台，受中央球铰约束，动平台具有3个转动自由度，可完成俯仰、倾斜等姿态的调整。动平台球铰中心构成等边三角形B1B2B3，定平台虎克铰中心构成等边三角形A1A2A3，三角形外接圆半径R1=380 mm，R2=510 mm，中央立柱高R3=1150 mm。

图1 电液驱动3-UPS/S并联稳定平台样机

1.1 运动学分析

构建惯性坐标系Ψ0、动坐标系Ψp及支链坐标系Ψi(i=1,2,3)，如图2所示。其中，惯性坐标系Ψ0和动坐标系Ψp的坐标原点位于中央球铰转动中心O；z轴垂直于定平台A1A2A3所在平面，x轴与ObA1平行；zp轴垂直于动平台B1B2B3所在平面，xp轴指向球铰转动中心B1。支链坐标系Ψi原点位于虎克铰转动中心Ai，zi轴沿着分支伸缩方向，yi轴垂直于平面OAiBi。动平台球铰转动中心Bi及定平台虎克铰转动中心Ai在惯性系下的位置矢量分别为bi、ai，分支矢量li=bi-ai，分支单位方向矢量si=li/|li|。

图2 电液驱动3-UPS/S并联稳定平台机构简图

采用T&T角[12]描述稳定平台的姿态，动坐标系Ψp相对于惯性坐标系Ψ0的旋转矩阵为

0pR=R(z，φ)R(y,θ)R(z,-φ)R(z,ψ)=

R(z,φ)R(y,θ)R(z,ψ-φ)

(1)

式中，φ为方位角；θ为倾斜角；ψ为扭转角。

支链坐标系Ψi相对于惯性系Ψ0的旋转矩阵由xi、yi和zi轴的方向余弦组成：

(2)

根据文献[13]，得到稳定平台驱动速度、支链角速度及支链与上平台铰链点速度：

(3)

式中，li为主动支链的长；ωp为动平台角速度；J为逆向雅可比矩阵。

稳定平台驱动加速度、支链角加速度及支链与上平台铰链点加速度分别为

(4)

利用数学恒等式[14]

a×(b×c)=(aTcE3-caT)b

(5)

式中，E3为一个3×3的单位矩阵。

可以得到支链下连杆Ai点的速度旋量：

(6)

同样，得到支链上连杆Bi点的速度旋量：

(7)

式中，S(·)为反对称矩阵。

动平台O点的速度旋量为

(8)

1.2 动力学模型的线性化形式

考虑到稳定平台3个主动支链具有相同的结构形式，将同一型号、同一规格的虎克铰、球铰、压力传感器及液压缸作为主要部件，且其他零部件制造具有较好的一致性，故3个主动支链的动力学参数相同，因此任选其中一个支链进行分析。构建动力学模型时，利用文献[9]、[15]的方法，对任选支链的上下连杆及动平台的动力学模型进行线性化处理。

为了简化辨识参数，利用下连杆在支链坐标系Ψi中相对于关键点Ai的惯性张量：

IA=diag(IAx，IAy，IAz)

(9)

此外，由于支链没有绕zi轴的转动，因此不需要对IAz进行辨识。得到支链下连杆动力学模型相对于惯性参数的线性化形式：

(10)

pd=[mdmdldc]TpA=[IAxIAy]T

同样，支链上连杆动力学模型相对于惯性参数的线性化形式为

(11)

式中，mu为上连杆质量；luc为上连杆质心到对应支链关键点Bi的距离；pu、pB为上连杆动力学参数；IBx、IBy为上连杆在支链坐标系Ψi中相对于Bi点的惯性张量元素。

动平台动力学模型相对于惯性参数的线性化形式为

(12)

1.3 摩擦模型的线性化形式

稳定平台的被动关节为球铰和虎克铰，被动关节处的摩擦力相较驱动关节液压缸处的摩擦力很小，因此忽略被动关节处的摩擦，仅考虑驱动关节液压缸处的摩擦。液压缸内存在两种形式的摩擦力[16]：由流体本身黏性引起的黏性摩擦力；液压缸活塞及活塞杆与液压缸内壁的密封接触引起的摩擦力。一般情况下，采用库仑摩擦力和黏性摩擦力对其进行描述，则第i个支链的摩擦力模型可以表示为

(13)

式中，Fci、Fvi分别为第i个支链的库仑摩擦力和黏性摩擦力。

黏性摩擦力与活塞杆运动速度呈线性关系：

(14)

式中，fvi为黏性摩擦因数。

库仑摩擦力主要来自活塞密封和缸筒内壁之间的摩擦以及活塞杆密封和活塞杆表面的摩擦，与密封产生的径向力成正比。本文中，液压缸作为机器人的运动支链，在运动过程中，除了提供动平台运动所需的轴向驱动力，还受到径向约束力。液压缸径向受力如图3所示，其中，Nti_1、Nti_2分别为活塞密封和活塞杆密封产生的径向力；Nni为支链径向约束力。库仑摩擦力模型可表示为

Fci=Fti+Fni=μi(Nti+Nni)

(15)

式中，Fti为密封系统产生的摩擦力，与密封系统的材料、特性等有关，属于液压缸固有参数；Fni为支链约束力产生的摩擦力；μi为摩擦因数；Nti为密封系统对活塞和活塞杆产生的径向力之和，Nti=Nti_1+Nti_2。

图3 液压缸径向受力图

由于平台各支链液压缸采用同一规格部件，因此各个液压缸密封产生的摩擦力以及黏性摩擦因数相同，可分别用Ft、fv表示，那么液压缸摩擦力模型为

(16)

将液压缸摩擦力模型转化为相对于摩擦参数的线性化形式：

(17)

选取pf=[Ftfv]T为摩擦参数，得到与机器人运动状态无关的独立的待辨识摩擦参数。

1.4 基本动力学参数

根据虚功原理，可以得到

(18)

F=[F1F2F3]TFf=[Ff1Ff2Ff3]T

式中，F、Ff分别为液压缸输出力和摩擦力。

将式(6)～式(12)代入式(18)，得到

JT(F-Ff)=JTFa=Φpm

(19)

式中，Fa为平台驱动力矢量。

观察矩阵Φ，由于支链上下连杆具有相同的角速度，因此将参数pA=[IAxIAy]T，pB=[IBxIBy]T进行组合，将组合后的IABx=IAx+IBx，IABy=IAy+IBy作为待辨识参数。此外，由于支链下连杆关键点速度及动平台线速度为0，因此矩阵Φ中相应的列向量为0，这就造成了此列向量对应的参数无法辨识，同时也说明了这些参数对机器人的动力学模型无影响，应进行简化，则可辨识的机器人惯性参数为

(20)

经过简化，得到稳定平台动力学模型相对于惯性参数的线性化形式：

Fa=F-Ff=Φbmpbm

(21)

式中，Φbm为简化后的参数矩阵。

结合驱动关节摩擦参数pf，得到3-UPS/S并联稳定平台待辨识的基本动力学参数：

pb=[pbmpf]T

(22)

2 辨识策略

由于3-UPS/S并联稳定平台工作空间较小，对其惯性参数及驱动关节摩擦参数进行分开辨识，设计不同的辨识策略。

2.1 惯性参数辨识

在参数辨识实验中，针对某一激励轨迹，需要采集大量的数据点，则式(20)变为超定方程组

(23)

简写为

Λ=Θpbm

(24)

式中，[1]、[2]、…[n]表示在第1、2…,n个采样点处测量；n为采样点数目；Θ为3n×9维的观测矩阵；Λ为实验测得的驱动力。

采用加权最小二乘法[6,17]对测量数据进行拟合，得到辨识参数的估计值

(25)

2.2 激励轨迹的优化

为避免复杂的正解计算，在稳定平台的姿态工作空间中对激励轨迹进行优化，这样可以利用运动学逆解直接得到各构件的位置、速度和加速度。

首先，参数化激励轨迹，一般采用有限的傅里叶级数进行参数化，但为了使轨迹运行初始和结束时刻平台的速度、加速度为0，避免辨识实验中出现颤振等现象而导致测量不精确，将五次多项式与傅里叶级数相结合[11]，得到参数化的激励轨迹为

(26)

式中，t为时间；aik、bik为傅里叶级数的参数；N为谐波数；ωf为轨迹的基频；Ami为五次多项式系数。

在姿态工作空间中优化激励轨迹，因此

[x1(t)x2(t)x3(t)]T=[θ(t)φ(t)ψ(t)]T

对式(26)求导，可以直接得到激励轨迹的速度和加速度表达式。

首先，给定如下激励轨迹开始和结束阶段运动学边界：

(27)

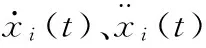
将运动学边界条件(式(27))代入式(26)，可以得到五次多项式系数：

然后，对激励轨迹进行优化，将观测矩阵条件数最小[8]作为优化准则，同时为了避免式(24)出现病态，对观测矩阵进行均衡化处理，最终得到优化目标函数：

fun=min(cond(Θeq))

(28)

Θeq=QΘD

式中，Θ为h×r维的矩阵；(Θ)i:为矩阵Θ的第i行元素；(QΘ):j为矩阵QΘ的第j列元素。

同时，需满足约束条件：

采用遗传算法进行优化求解，得到参数aik、bik，代入式(26)，可获得满足要求的激励轨迹。

最后，按照激励轨迹进行实验，采集数据，利用2.1节所述方法辨识出平台的惯性参数。

2.3 摩擦参数辨识

(29)

根据式(17)，令动平台分别以ωj1、ωj2(j1,j2=1,2,…,m;j1

(30)

对于整个运行轨迹s1，综合平均3个液压缸采样点数据，得到黏性摩擦因数：

(31)

之后，将摩擦力模型改写为关于Ft的线性化形式：

(32)

利用最小二乘法辨识密封系统摩擦力Ft，设计轨迹s2，采集传感器信号，结合已辨识出的参数，式(32)改写为

Λf=ΘfFt

(33)

式中，Λf为测量数据；Θf为观测矩阵。

得到密封系统摩擦力Ft估计值，为

(34)

3 辨识实验

3.1 辨识实验平台

本文选用NI cRIO-9068控制器，采用PID控制进行辨识实验，如图4所示。其中，液压缸压力传感器型号为BD/SENSOR17.600G；液压缸活塞杆连接的测力传感器型号为LH-S05；测量动平台姿态变化的双轴同步测量倾角仪型号为AGS-XR13-S11-P215。

图4 辨识实验框图

3.2 辨识轨迹

(1)惯性参数辨识激励轨迹。在稳定平台姿态工作空间进行激励轨迹的优化，这样可避免计算机器人的正解，仅采用逆解便可得到运动构件的位置、速度、加速度，提高了辨识的效率。考虑到本文研究的稳定平台主要功能为水平姿态的调整，为了保证其具有较大的姿态工作空间，在平台工作过程中扭转角ψ基本维持恒定，其绕zp轴的惯性力对动力学模型影响较小，从简化辨识过程考虑，不对平台转动惯量Ipz进行辨识。基于此，采用双轴同步测量倾角仪，测量平台倾斜角度θ及偏转角度φ。令x1=θ,x2=φ，设置傅里叶级数基本频率ωf=0.628 Hz，谐波数N=4，则周期tf=10 s。利用遗传算法优化得机器人在ψ=30°时的激励轨迹，如图5所示。设置采样频率为每秒105次，将传感器测量的数据进行滤波处理，根据式(25)辨识出机器人的惯性参数pbm。

(a)激励轨迹

(b)激励轨迹投影

(2)黏性摩擦因数辨识轨迹s1。给定机器人初始姿态θ=10°，φ=0°，ψ=30°，令其动平台分别以角速度ω1=5°/s，10°/s，15°/s，20°/s绕z轴匀速转动360°,即φ∈[0°，360°]。在此段轨迹s1上，每隔15°设置一个采样点，共设置24个采样点，采集液压缸压力传感器及活塞杆处测力传感器信号，滤波处理后根据2.3节所述方法，由液压缸活塞直径40 mm、活塞杆直径25 mm，摩擦因数μ=0.02，辨识出黏性摩擦因数fv。

(3)密封系统摩擦力辨识轨迹s2。给定机器人初始姿态θ=10°，φ=0°，ψ=30°，令动平台沿θ=20sin(πt/2)轨迹运动，采集传感器信号，滤波处理后利用最小二乘法辨识出密封系统摩擦力Ft。

3.3 辨识结果及验证

通过辨识实验，得到电液驱动3-UPS/S并联稳定平台惯性参数及摩擦参数的辨识结果，如表1所示。

表1 参数辨识结果

对参数辨识结果进行验证：给定任意轨迹，为保证测量数据的准确性，令平台多次、重复运行这一轨迹，根据力传感器和压力传感器测量值，进行数据处理，得到实测值与理论计算值对比，如图6、图7所示,图中输出力和驱动力的正值表示力方向为液压缸推出方向，负值表示力方向为液压缸缩回方向。其中，压力传感器测得的数据为液压缸两腔的压力，根据两腔有效作用面积，可计算得到液压缸的输出力，图7中，被标记为“实测值”。

(a)第一分支驱动力

(b)第二分支动支力

(c)第三分支驱动力

(a)第一分支液压缸输出力

(b)第二分支液压缸输出力

(c)第三分支液压缸输出力

从图6、图7可以看出，依据本文的辨识结果计算得到的驱动力及液压缸输出力与传感器实际测量值符合度较高，基本一致，验证了辨识结果的可靠性及辨识策略的可行性。

5 结语

本文对基于3-UPS/S并联机器人的电液驱动稳定平台惯性参数及摩擦参数进行了全面辨识。建立了各运动构件动力学模型关于惯性参数的线性化形式，得到了待辨识的惯性参数；通过驱动关节摩擦力分析，建立了摩擦力模型关于摩擦参数的线性化形式，提取出了与平台运动状态无关的待辨识摩擦参数，保证了辨识结果的独立性、合理性。在辨识惯性参数的激励轨迹优化中，采取多项式结合傅里叶级数的方法，在平台姿态工作空间得到了严格满足运动学边界条件的激励轨迹，

保证了实验中机器人的平稳运行，同时避免了并联机器人复杂的正解计算，简化了辨识过程。最后通过实验得到了平台的惯性参数及摩擦参数的辨识结果，并利用任意轨迹验证了辨识结果合理性和可靠性。

[1] 程佳. 并联4TPS-1PS型电动稳定跟踪平台的特性及控制研究[D]. 杭州: 浙江大学, 2008.

[2] Díaz-Rodríguez M, Valera A, Mata V, et al.Model-based Control of a 3-DOF Parallel Robot Based on Identified Relevant Parameters[J]. IEEE/ASME Transactions on Mechatronics, 2013, 19(6): 737-1744.

[3] Abdellatif H, Heimann B. Experimental Identification of the Dynamics Model for 6DOF Parallel Manipulators[J]. Robotica, 2010, 28(2):359-368.

[4] Pàmies-Vilà R, Font-Llagunes J M, Lugrís U, et al.Parameter Identification Method for a Three-dimensional Foot-ground Contact Model[J]. Mechanism and Machine Theory, 2014, 75(5):107-116.

[5] Jin J, Gans N. ParameterIdentification for Industrial Robots with a Fast and Robust Trajectory Design Approach[J]. Robotics and Computer-Integrated Manufacturing, 2015, 31:21-29.

[6] Díaz-Rodríguez M, Mata V, Valera A, et al. A Methodology for Dynamic Parameters Identification of 3-DOF Parallel Robots in Terms of Relevant Parameters[J]. Mechanism and Machine Theory, 2010, 45:1337-1356.

[7] Chen C T, Renn J C, Yan Z Y. Experimental Identification of Inertial and Friction Parameters for Electro-hydraulic Motion Simulators[J]. Mechatronics, 2011, 21(1):1-10.

[8] 吴军. 四自由度冗余混联机床的分析、辨识及控制[D]. 北京：清华大学, 2007.

[9] 黄田, 陈闯, 王辉. 一种新型并联动力头动力学参数辨识方法研究[J]. 机械工程学报, 2013, 49(19):31-39. Huang Tian, Chen Chuang, Wang Hui. Identification of Dynamic Parameters of a Novel 3-DOF Spindle Head[J]. Journal of Mechanical Engineering, 2013, 49(19): 31-39.

[10] Park K J. Fourier-basedOptimal Excitation Trajectories for the Dynamic Identification of Robots[J]. Robotica, 2006, 24(1): 625-633.

[11] 吴文祥, 朱世强, 靳兴来. 基于改进傅里叶级数的机器人动力学参数辨识[J]. 浙江大学学报(工学版)，2013，47(2):231-237.

Wu Wenxiang, Zhu Shiqiang, Jin Xinglai. Dynam-ic Identification for Robot Manipulators Based on Modified Fourier Series[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(2):231-237.

[12] Bonev I A. A New Approach to Orientation Workspace Analysis of 6-DOF Parallel Manipulators[J]. Mechanism and Machine Theory, 2001, 36(1): 15-28.

[13] 李新友, 陈五一, 韩先国. 基于Kane方程的3UPS/S并联机构动力学研究[J]. 机床与液压, 2011, 39(13):1-5. Li Xinyou, Chen Wuyi, Han Xianguo. Dynamic Analysis of a 3UPS/S Parallel Mechanism Based on Kane Equations[J]. Machine Tool and Hydraulics, 2011, 39(13):1-5.

[14] 陈闯. 新型三坐标并联动力头的数控系统开发与研究[D]. 天津: 天津大学, 2013.

[15] Wu J, Wang J S, Wang L P, et al. Dynamic Formulation of Redundant and Nonredundant Parallel Manipulators for Dynamic Parameter Identification[J]. Mechatronics, 2009, 19(4):586-590.

[16] 刘静, 甘屹, 潘双夏. 基于虚拟样机的挖掘机器人液压缸内摩擦力确定方法研究[J]. 机械设计, 2008, 25(8):30-32. Liu Jing, Gan Yi, Pan Shuangxia. Research on the Friction of the Hydraulic Cylinder of the Digging Robot Based on the Virtual Prototype[J]. Journal of Machine Design, 2008, 25(08):30-32.

[17] Shang W, Cong S, Kong F. Identification of Dynamic and Friction Parameters of a Parallel Manipulator with Actuation Redundancy[J]. Mechatronics, 2010, 20(2):192-200.

(编辑 张 洋)

Identification of Dynamics Parameters for an Electro-hydraulic 3-UPS/S Parallel Stabilized Paltform

Guo Fei1,2Li Yongquan2,3Li Yukun2,3Zhang Yu1,2Zhang Lijie1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control，Yanshan University，Qinhuangdao，Hebei，066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science，Ministry of Education，Yanshan University，Qinhuangdao，Hebei，0660043.Parallel Robot and Mechatronic System Laboratory of Hebei Province,Yanshan University, Qinhuangdao，Hebei，066004

An electro-hydraulic parallel stabilized paltform was selected as the research object, and the inertia and friction parameters of the system were identified via the experiments. The identification model for the inertia parameters was obtained by screw equivalence principle and virtual work principle, and the exciting trajectory was designed by Fourier series which was modified by quintic polynomial and optimized. The intrinsic friction parameters were separated from the friction model, the identification model for the friction parameters was built, and the exciting trajectories were planned. The identification results were obtained by the experiments, and verified through an arbitrary trajectory.

parameter identification; parallel robot; excitation trajectory; dynamics

2015-04-27

国家自然科学基金资助项目(51275438， 51405421)；河北省自然科学基金资助项目(E2011203214)

TP242

10.3969/j.issn.1004-132X.2016.21.005

郭 菲，女，1986年生。燕山大学机械工程学院博士研究生。主要研究方向为并联机构性能指标、动力学及参数辨识。发表论文9篇。李永泉，男，1979年生。燕山大学机械工程学院副教授。李玉昆，男，1978年生。燕山大学机械工程学院高级实验师。张 宇，男，1990年生。燕山大学机械工程学院硕士研究生。张立杰(通信作者)，男，1969年生。燕山大学机械工程学院教授、博士研究生导师。