基于退化过程的矿用自卸车货箱磨损预测分析
2016-12-24申焱华魏福林石博强
申焱华 魏福林 石博强
北京科技大学,北京,100083
基于退化过程的矿用自卸车货箱磨损预测分析
申焱华 魏福林 石博强
北京科技大学,北京,100083
利用离散元法和有限元法的联合仿真,模拟矿用自卸车的卸货过程,求取了卸货过程中货箱底板各单元滑动磨损的时间历程。将磨损高度的变化设为连续随机动态过程,利用几何布朗运动建立了货箱磨损的退化模型。应用极大似然估计法和贝叶斯后验分布,计算底板各单元磨损高度变化的漂移率和波动率,实现对货箱底板磨损行为的预测。
自卸车货箱;磨损;几何布朗运动;预测
0 引言
矿用自卸车货箱直接与矿石相接触,而矿石在卸货过程中会造成货箱的严重磨损,因此磨损是货箱常见的失效形式之一[1]。通过分析具体货箱结构形式下的磨损行为,探索延长货箱寿命的有效方法,改善货箱磨损的现状,可降低矿用自卸车的使用成本,提高资源利用率。
有关自卸车货箱磨损的文献较少,文献[2-3]通过光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法处理大变形和有限元方法(finite element method,FEM)的联合仿真,对宽体自卸车两种货箱结构的磨损特性进行了对比,给出了一次卸货后货箱磨损的最大位置,以及冲击角与货物流动的关系,但其采用的Archard模型描述的是磨损量同施加的载荷的关系[4],不能对货箱在整个服役期内的长期磨损行为进行分析。
考虑到确定性的Archard模型难以对机构磨合期的各个阶段进行描述,文献[5]将Archard 模型中的磨损因数分别看作随机变量和随机过程,对表面磨损特性进行了分析对比。文献[6]利用人口增长模型,对机械结构磨合期中粗糙表面的磨损变化进行了建模。文献[7]应用Markov链和Gamma分布分析了管道的腐蚀增长行为。文献[8]根据测试的数据建立了地下管道腐蚀特性随机动态模型,对管道腐蚀程度的变化特性进行了研究。卸货过程中货箱的磨损可认为是底板材料损失的演化行为,是一种与时间有关的退化过程。因此,需采用随机动态过程对服役期内的货箱底板磨损情况进行准确描述。
本文以110 t矿用自卸车货箱为分析对象,应用离散元法及有限元法对卸货过程中货箱底板的磨损进行分析。采用随机微分方程对货箱底板各微单元区域的磨损变化进行建模,以描述货箱底板磨损高度的长期演化行为。
1 基于离散元的货箱底板磨损
1.1 自卸车卸货过程中的底板磨损
矿用自卸车卸货过程中,堆积的矿石与车厢钢板(包括对底板、侧板)间的干摩擦产生的磨料磨损的实质是,矿石中硬的颗粒或突出物在与车厢钢板表面相互接触运动过程中,使钢板表面材料发生损耗的一种现象或过程。矿石作用在钢板表面的力可以分解为切向力和法向力,其中,切向力推动矿石向前运动,法向力使矿石压入钢板表面。具有一定形状的矿石在沿自卸车货箱底板滑动的过程中,矿石与底板间的磨损行为使得钢板表面发生微细的划痕或磨沟,从而使钢板的厚度不断减小,宏观表现为磨损表面比较光亮。此为矿用自卸车车厢货箱最为常见的磨损。
Archard磨损模型是基于接触力学机理建立的,其一般形式为
(1)
式中,V为磨损量,m3;s为滑移距离,m;K为磨损因数;Fn为法向载荷,N;H为接触面金属材料的硬度,MPa。
应用式(1)对货箱一次卸货过程中矿石与货箱底板的磨损行为进行描述,采用磨损深度的评价指标将Archard磨损模型变更为
dh/dt=kpvs
(2)
式中,h为磨损深度,m;k为磨损系数;p为接触压力,Pa;vs为滑移速度,m/s。
由式(2)可知,磨损深度的变化与作用在底板上的接触压力、矿石与底板间的滑移速度以及矿石材料的特性有关,通过测量取得各参数的变化值,即可分析卸货过程中底板磨损的变化规律。
1.2 基于离散元的货箱底板磨损分析
离散元法认为系统由离散的个体组成,并将个体的形态简化为具有独立尺寸和质量的球体,通过设置某种接触模型,描述球体之间发生接触与脱离时的接触力与能量的关系,以此来计算大量颗粒在给定条件下的运动规律。考虑到矿用自卸车货箱装载的矿石是典型的散体物料,利用离散元法描述其散体物料的运动规律,求取卸货过程中矿石与货箱底板间的不断相对滑移运动导致的底板磨损。
采用基于离散元理论设计的EDEM仿真软件对货箱卸货过程中的底板磨损行为进行模拟。根据矿用自卸车的吨位、矿石铲斗的大小,可确定货箱装载的矿石体积,并将矿石表现为具有一定粒度分布的离散个体。EDEM软件中嵌入了基于Archard磨损模型的Hertz-Mindlin接触模型,可用于计算货箱卸货过程中散体物料的运动和受力情况。仿真过程中,设定货箱的举升角速度为常数,采用EDEM中的球形颗粒模拟矿石的形态,忽略掉货物几何形状不规则等因素。以载重量为110 t某型矿用自卸车货箱为分析对象,本文中所用的矿石颗粒大小不一,呈半径均值为90 mm的正态分布,矿石的密度为2790 kg/m3。按照矿用自卸车实际服役环境和工况需求,在货箱装载过程中设置铲斗相对货箱的位置,根据货箱及所配铲斗的容量,铲装5次装满货箱。
110 t矿用自卸车货箱底板倾角为12°,货箱侧面钢板厚8 mm,底板厚12 mm,所用钢板材料均为Q345钢。为分析离散颗粒与货箱底板任一小区域之间的磨损关系,借助有限元的单元网格划分思想,对货箱进行离散单元化处理。通过对底板各单元内磨损量的分析,得出卸货过程中底板各区域的磨损大小。利用有限元前处理软件Hypermesh对货箱进行网格划分,对货箱的前板、底板、侧板和护沿进行网格划分,单元类型为壳单元Shell63,单元尺寸为100 mm。
110 t矿用自卸车为货箱配备了三级举升油缸,按照三级举升油缸的作动时间及最大举升角度,模拟矿石在其自重的作用下实现货箱卸载的过程。卸载后,以货箱底板为分析对象,将底板的网格单独选择出来作为一个集合,进行各单元磨损的分析。图1为货箱卸货各个时刻底板(俯视图)磨损量和货物状态的示意图。对比分析可知,卸货起始阶段,磨损量较大的部位集中在底板前端,随着货箱倾斜角度的加大,货箱中部和尾部的磨损量加大。从整个过程看,磨损量最大值的位置处于货箱前端的部分区域。

(a)举升2 s

(b)举升6 s

(c)举升12 s

(d)举升16 s

图1 矿用自卸车货箱卸载过程
为考察底板不同位置处磨损量的时间变化历程,在底板的不同区域设置17个单元作为观测点,如图2所示。

图2 单元磨损测试点
图3所示为卸载过程中17个观测点磨损量的时间历程曲线。根据货箱的结构及货物的堆装特点,其货箱前部底板处的载荷量大。在举升油缸举升货箱的起始时段,货箱前部区域中的货物首先开始滑动,待货箱举升到一定角度时,货箱底板前端的矿石基本通过抛掷,或沿底板滑移至货箱底板的后半部分,货箱前部区域的磨损量不再增加。该阶段货箱底板中部的载荷量变化不大,因此该区域磨损量的增加比较平缓;同样,货箱底板的尾部与底板中部的变化也与此类似。在货箱举升的后半时段,矿石堆积在底板尾部,使得该区域的磨损量在举升前期增加缓慢,而在举升后期的较短时间有个快速增加的过程,该区域磨损量的大小基本等同于货箱中部区域的磨损量。前部区域的载荷量大,单个最大磨损量的位置出现在货箱的前部区域,但前部区域整体的磨损量不如底板尾部磨损的均匀。
2 基于退化过程的货箱底板长期磨损行为分析
货箱服役过程中,其卸货过程的磨损是不断损失或破坏的过程,钢板表面的厚度直接耗失和材料的转移(材料从钢板的表面转移到矿石的表面),使得钢板的表面产生残余变形。不断损失或破坏说明了磨损过程连续性和规律性。货箱底板每个单元上的磨损时间历程可视为是一个动态随机过程,通过对磨损过程的建模,可预测其在服役过程中每个单元磨损情况的变化趋势。
本文将磨损过程中底板高度的改变量,作为对货箱磨损量的评价指标。布朗运动及伊藤过程常用来描述具有退化扩散性质的物体演变过程,将货箱底板各单元磨损高度的变化看作连续随机动态过程,建立基于几何布朗运动的磨损预测模型。该模型可给出各时间货箱底板磨损量的大小,能较

(a)测试点磨损变化历程1

(b)测试点磨损变化历程2

(c)测试点磨损变化历程3
好地描述底板厚度受磨损影响退化演变的过程。
2.1 几何布朗运动
如果连续函数xt满足
dxt=μ(xt,t)dt+σ(xt,t)dwt
(3)
式中,wt表示一个标准布朗运动,wt~N(0,t);μ(xt,t)、σ(xt,t)分别为漂移函数和扩散函数。
则称式(3)描述的过程为伊藤过程[9]。
若式(3)中的μ(xt,t)=μxt,σ(xt,t)=σxt,其中,漂移率μ、波动率σ均为常数,则称该形式的伊藤过程xt为几何布朗运动。
设G(xt,t)=lnxt,利用伊藤引理[9]得到
dlnxt=(μ-σ2/2)dt+σdwt
(4)
将式(4)两边取积分可得
故
lnxt=lnx0+(μ-σ2/2)t+σwt
(5)
由式(5)可求取几何布朗运动xt的时间历程函数的表达式:
(6)
可以证明,lnX(t)是一个均值为lnX(0)+(μ-σ2/2)t、标准差为σt1/2的正态分布函数。因此,利用lnxt的正态分布特性,可求取漂移率μ和波动率σ,进而预测几何布朗运动xt的演化规律。
2.2 货箱底板磨损过程的建模
矿用自卸车货箱满载时呈现堆装形态,货箱前段区域中的矿石载重量大,使得底板各处的垂向载荷大小不同,由式(2)可知,卸货过程中底板各处的磨损量不一。为分析底板各单元的长期磨损行为,设Zij(t)为t时刻(可对应于货箱的卸货的次数)底板单元(i,j)处的轮廓高度。矿石与货箱底板间的磨损行为导致了底板厚度的不断减小,可将其认为是一个随时间的退化过程。设式(3)中的漂移率和波动率均为常数,利用几何布朗运动建立底板各单元高度的变化过程:
dZij(t)=μijZij(t)dt+σijZij(t)dBij(t)
(7)
由图3显示的磨损量和底板轮廓的几何关系可知,任一单元处的磨损量Wij(t)为初始高度与t时刻的轮廓高度Zij(t)之差,应用式(6)、式(7),可得
(8)
式中,Zij(0)为货箱底板各单元的初始轮廓高度(110 t矿用自卸车货箱底板设计厚度为10 mm);μij、σij分别为底板单元(i,j)磨损过程中的漂移率和波动率。
由式(8)可知,若能求取底板单元(i,j)磨损高度时间历程的漂移率和波动率,则能预测一定时间尺度下货箱底板各个区域的磨损情况。
2.3 单元磨损高度的漂移率与波动率估计
为对货箱底板磨损的行为进行长期预测,间隔一定时间或卸货次数对货箱底板的各单元厚度进行采样,可获取底板单元(i,j)磨损量的时间变化序列Wij(t)。假设该序列Wij(t)满足几何布朗运动条件[6],利用极大似然估计法求取n次卸货过程中磨损高度历程的漂移率μij与波动率σij。

令W=[w1w2…wn]T,t=[t1t2…tn]T。由于lnw(ti)服从正态分布,其均值和协方差分别为
(9)

(10)
lnW=[lnw1lnw2… lnwn]T
(11)
(12)

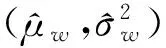
为了对货箱服役期间底板磨损的长期行为进行预测,在确定了先验分布lnw(ti)的情况下,可采用贝叶斯后验分布方法,利用新的测试或仿真数据对漂移率和波动率进行实时更新。
将tk时刻获取的该单元的所有数据记为
W1∶k={w(tj),1≤tj≤tk}

由于lnw服从正态分布,因此,tk时刻对随机参数φ更新后的结果为
(13)
(14)
对各单元的磨损而言,每监测获取一个磨损量数据,就可利用式(13)、式(14)对各单元的随机参数(漂移率和波动率)进行一次更新,从而实现对参数的实时更新。
3 基于退化过程的货箱底板磨损预测分析
3.1 货箱底板一单元的磨损趋势预测
假定货箱每次的装载量及堆积形状均相同,对于货箱底板上的任意一个单元,可以认为每次卸货过程中,该单元磨损量的时间历程曲线均相同。根据预测时间尺度的不同,可选取不同的时间间隔进行磨损量的测取。本文以10次卸货为例,测取每次卸货后货箱底板各单元处的磨损量变化,形成分析所用的时间历程曲线。利用式(11)、式(12)求取先验分布中的参数,进而估计该单元的漂移率和波动率。根据式(6),可绘制出货箱表面轮廓高度随时间变化曲线,如图4所示。

图4 单元1298的磨损量变化趋势
矿石与底板的长期滑动磨损过程会导致钢板变薄,从而使货箱底板结构以及矿石磨损行为发生改变,进而导致磨损量的漂移率和波动率改变。根据新测试的各单元的磨损量,可利用贝叶斯后验分布的公式计算下一时段磨损量的漂移率和波动率。
3.2 货箱磨损模型在二维平面内的磨损趋势预测
为考察底板整个区域上的磨损规律,将货箱底板上所有网格单元估计出来的漂移率和波动率代入磨损数学模型(式(7)),并且结合网格单元的空间坐标信息,可对货箱底板高度受磨损影响的演变过程进行仿真和预测。
考虑到货箱底板各处所承受的载荷量不同,以及卸货过程中底板各区域物料滑移状态的不同,使得底板某些区域的磨损量会比其他部位大一些。如图5所示,从货箱底板整体看,其货箱前部个别地方会出现磨损量的最大值,但随着货箱服役时间的加长,货箱后半段磨损区域较均匀,该区域整体的磨损量要高于其他区域。

图5 货箱底板磨损量分布图 (t=5000s)
本文采用的多次卸货过程中底板各单元磨损量的变化曲线,是将货箱一次卸货后各单元的磨损量进行多次线性叠加得到的。实际应用中,应每隔一段时间测量各单元的磨损量,以此为基准计算各单元磨损量的漂移率与波动率,从而对货箱底板磨损量的长期演变行为进行预测。
由货箱的结构强度分析可知,为保证装载工况下货箱结构的安全,对货箱底板的最小厚度有一定的要求。通过磨损高度的时间演化曲线,可估计出货箱在使用过程中的剩余寿命,并制订相应的维修策略。
4 结语
本文基于离散元法和有限元法对矿用自卸车货箱卸货过程的磨损进行了联合仿真,仿真结果显示出各微观区域在卸货过程中磨损量的变化。在卸货过程中,货箱底板前端矿石物料的移动有别于中部和尾部,会出现磨损量的最大值;货箱尾部区域矿石与底板间的磨损持续时间较长,该区域各单元的磨损量大小基本相同。
对于货箱服役期内底板磨损的长期行为,利用几何布朗运动对货箱底板磨损高度的变化进行建模,通过货箱多次卸货底板磨损的数据,利用极大似然估计,得到各单元磨损高度变化的漂移率和波动率,从而对货箱底板各微单元的磨损量随时间的演化过程进行预测。根据货箱的可靠性指标,并基于底板高度的磨损退化过程可对其磨损均值进行预测。
本文仅以货箱底板的磨损为研究对象,可使用相同的方法对货箱的侧板磨损进行分析预测。进一步,可对不同货箱结构类型的磨损量及长期磨损演化行为进行分析,为货箱的优化设计提供参考依据。
[1] 冯明,闫军利,高利军,等. 非公路矿用自卸车车厢上耐磨材料的应用[J]. 矿业装备,2012(10):57-59. Feng Ming, Yan Junli, Gao Lijun, et al. The Application of Wear-resistant Material on the Non Highway Dump Truck Compartment[J]. Journal of Mining Equipment, 2012(10):57-59.
[2] Forsström D,Lindbäck T,OnsénP J. Prediction of Wear in a Dumper Truck Body by Coupling SPH-FEM[J]. Tribology, 2014,8(2):111-115.
[3] Forsström D,Jonsén P. Load Intensity Calculations on Tipper Body Using DEM FEM Coupling[C]//11th World Congress on Computational Mechanics. Barcelona, Spain, 2014:1612-1621.
[4] Archard J F. Contact and Rubbing of Flat Surfaces[J]. Journal of Applied Physics,1953, 24(8):981-988.
[5] Dasilvajr C,Pintaude G. Uncertainty Analysis on the Wear Coefficient of Archard Model[J]. Tribology International, 2008,41: 473-481
[6] Wang Zhanjiang, Zhou Qinghua. Applying a Population Growth Model to Simulate Wear of Rough Surfaces during Running-in[J]. Wear, 2012, 294:356-363.
[7] Caleyo F,Vela’zquez J C,Valor A,et al. Markov Chain Modelling of Pitting Corrosion in Undergro-und Pipelines[J]. Corrosion Science, 2009,51(9): 2197-2207.
[8] Oksendal B. Stochastic Differential Equations: An Introduction with Applications[M]. 6 ed. Berlin:Springer-Verlag,2003.
[9] Si X S,Wang W,Hu C H,et al. Remaining Useful Life Estimation Based on a Nonlinear Diffusion Degradation Process[J]. IEEE Transactions on Reliability, 2012, 61(1):50-67.
(编辑 张 洋)
Wear Prediction Analysis of Mining Dump Truck Body Based on Degradation Processes
Shen Yanhua Wei Fulin Shi Boqiang
University of Science and Technology Beijing,Beijing,100083
The dumping processes of a dump truck were simulated by coupling the discrete element method and the finite element method. The abrasive wear time series of each grid on the bottom floor was obtained by the co-simulation results. Wear height variation of bottom floor was regarded as the stochastic dynamic process, and the geometric Brownian motion was used to build the degradation model of body wear. The drift and diffusion coefficients of wear height on each grid were calculated by maximum likelihood estimation and Bayesian posterior method. The wear behavior evolution of the body floor may be predicted based on the degradation model.
dump truck body; wear; geometric Brownian motion; prediction
2015-12-30
国家科技支撑计划资助项目(2008BAB32B03);国家自然科学基金资助项目(51075029)
U463.84
10.3969/j.issn.1004-132X.2016.21.002
申焱华,女,1968年生。北京科技大学机械工程学院副教授。主要研究方向为车辆设计与研究、现在设计方法。发表论文40余篇。魏福林,男,1991年生。北京科技大学机械工程学院硕士研究生。石博强,男,1962年生。北京科技大学机械工程学院教授、博士研究生导师。
