2PRS-2PSS并联机构的设计与运动学分析

张彦斌 丁 丁 吴 鑫 王增辉 赵浥夫

河南科技大学，洛阳，471003



2PRS-2PSS并联机构的设计与运动学分析

张彦斌 丁 丁 吴 鑫 王增辉 赵浥夫

河南科技大学，洛阳，471003

设计出一种两移动两转动的四自由度2PRS-2PSS并联机构。以该机构的4条分支运动链的主动移动副轴线与静平台的夹角为变量。首先根据方位特征集理论分析了该并联机构的运动输出特性；再基于矢量法对其运动学进行分析，推导出机构的位置和姿态的正解、逆解，进而推导出其速度和加速度方程；然后基于机构雅可比矩阵的奇异性，详细讨论了机构可能存在的奇异位形；最后，通过算例仿真验证了理论分析的正确性。

并联机构；自由度；运动学分析；奇异性

0 引言

近年来，并联机构的应用越来越广泛，但多数情况下不需要全部的6个自由度，因此设计满足使用要求的少自由度并联机构成了本领域的研究热点[1-4]。在实际应用中，往往根据不同的工作需求选择相应自由度类型的并联机构，例如具有3个自由度的DELTA[5]机器人已在包装、医药工业上广泛应用，而五自由度并联机构多用在数控加工中心[6]。空间四自由度并联机构是少自由度并联机构中的一个重要分支，根据动平台运动输出特性的不同，四自由度并联机构可以划分为3种类型，即三移动一转动型[7](3T1R)、一移动三转动型[8](1T3R)、二移动二转动型(2T2R)。空间2T2R型并联机构同时具有2个移动自由度和2个转动自由度，能够完成较为复杂的动作，已有不少学者对此类机构进行研究[9-10]。马履中等[11]设计出一种基于2T2R型并联机构的减振装置，刘剑敏等[12]提出一种基于2T2R型并联机构的振动筛，但文献[11-12]中的机构均含有一个混合运动链，增加了机构的装配难度。Kumar等[13]设计出一种可用于医用注射的2T2R并联机构装置，其机构结构为3-5R，其中的一条链中有2个主动副，故必有1个驱动器不能安装在机架，增加了机构的转动惯量。范彩霞等[14]根据构型演变和李群理论综合出一类2T2R型并联机构。

上述文献中所提到机构的装配构型具有单一性，所建立的运动数学模型无法解决某一类机构的问题。因此本文提出一类2T2R型四自由度2PRS-2PSS并联机构，推导出该并联机构的运动学方程(位置、姿态、速度和加速度)，详细讨论了机构可能存在的奇异位形，并进行了基于虚拟样机和理论编程的仿真，验证了理论分析的正确性。

1 结构设计

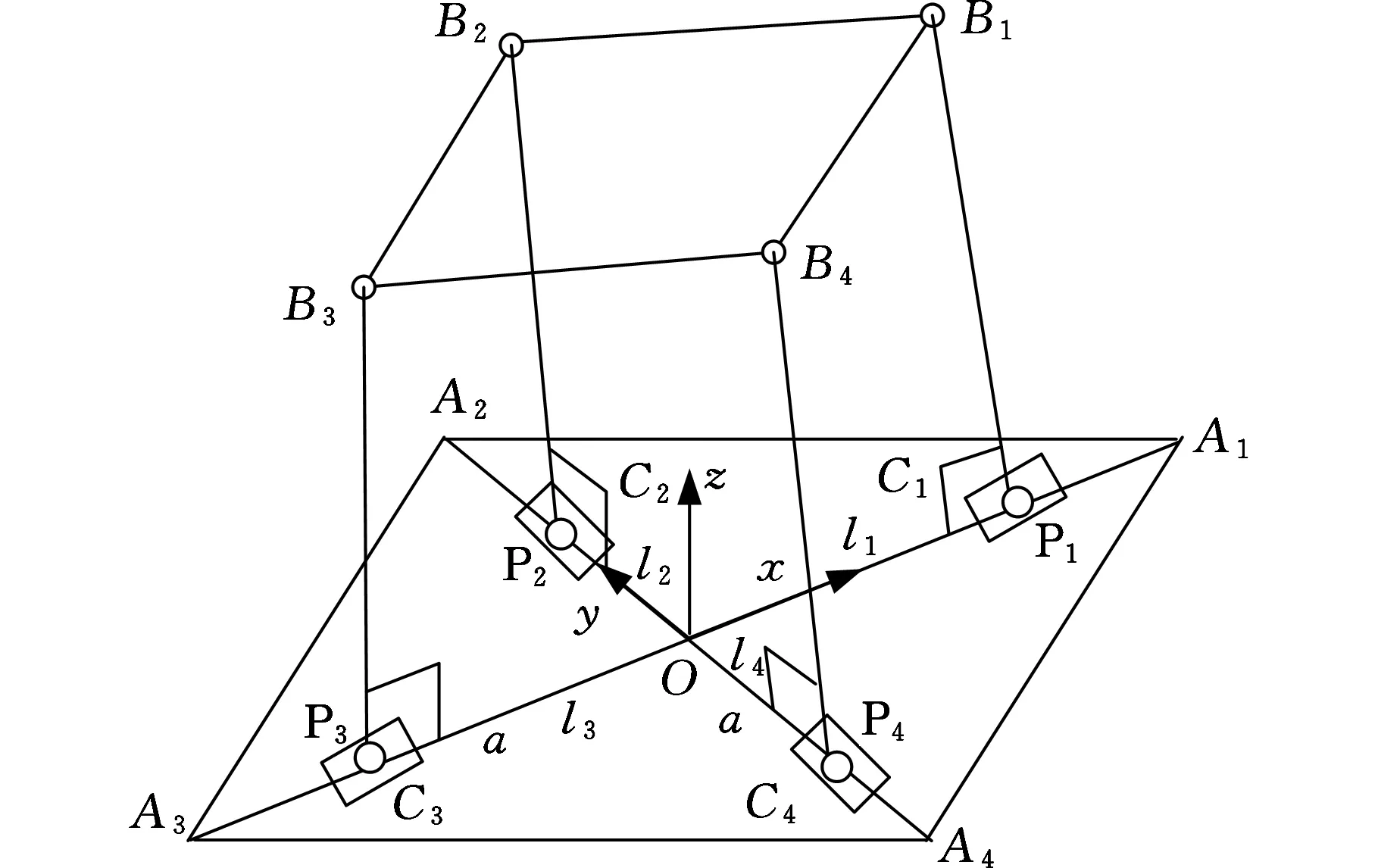
如图1所示，新型四自由度并联机构由动平台、静平台，以及连接两平台的4条运动支链组成，机构的三维CAD模型如图2所示。支链一(A1C1B1)和支链三(A3C3B3)的结构相同，均由移动副、转动副和球副依次连接而成，且同一支链内移动副与转动副的轴线相互垂直，记为{P⊥R-S}，同时，支链一和支链三中的2个转动副轴线相互平行。支链二(A2C2B2)与支链四(A4C4B4)的结构也相同，从静平台到动平台运动副配置依次为移动副、球副和球副，记为{P-S-S}。机构的动平台为正方形平板B1B2B3B4，4条支链末端的球副分别安装于动平台上的Bi(i=1，2，3，4)点，4个移动副的轨道与静平台相交于Ai点，4个交点的连线构成正方形A1A2A3A4。机构4个主动移动副的轨道中心线与静平台夹角(变量)为θ。θ取不同值时，对应2PRS-2PSS并联机构的特定装配形式。尽管这些装配形式下的机构运动特性不尽相同，但它们却具有统一的运动学方程。因此，该并联机构的设计和运动学分析适用于一类2PRS-2PSS机构，具有广义性和普遍意义。

图1 新型四自由度并联机构

图2 并联机构的CAD模型

2 机构运动输出特性分析

方位特征集法[15]是分析并联机构的一种简单而有效的方法，本文采用该方法对机构的运动输出特性进行分析。

根据图1所示机构4条支链的运动副配置关系，可得支链一与支链三，支链二与支链四的拓扑结构：

SOC{-Pj1⊥Rj2-Sj3} (j=1, 3)

(1)

SOC{-Pk1-Rk2-Sk3}(k=2, 4)

(2)

按照机构装配条件，支链一与支链三、支链二与支链四末端的方位特征集分别为

(3)

(4)

其中，左下标数字表示支链的特征自由度数；t、r分别表示移动、转动。如2t(⊥R12)表示垂直于R12轴线方向的2个移动自由度，1r(//Ri2)表示支链在平行于Ri2轴线的方向存在1个非独立的转动自由度。Oi3表示第i条支链与动平台连接的球副的球心。连接B1B3、A1A3，如果将A1A3看作是固定机架，B1B3看作是连杆，则A1C1B1B3C3A3可视为平面六杆机构，故该六杆机构的输出杆件B1B3只能做三自由度平面运动。但由于连杆B1B3两端的B1和B3位置处均为球副，所以连杆B1B3绕其轴线方向存在1个局部转动自由度。因此支链一与支链三组成的子并联机构的方位特征集为

(5)

同理，由支链二和支链四组成的子并联机构的方位特征集为

(6)

由于并联机构动平台的运动输出特性是所有支链运动输出特性的交集，所以该并联机构动平台的方位特征集为

(7)

式(7)表明动平台具有2个移动自由度和2个转动自由度，即该机构为2T2R四自由度并联机构。

3 运动学分析

如图1所示，定坐标系Oxyz固结在静平台上，坐标原点O与正方形A1A2A3A4的形心重合，x轴、y轴分别与对角线A1A3和A2A4共线，z轴垂直于静平台向上。动坐标系Puvw则固结于动平台上，坐标原点P与正方形B1B2B3B4的形心重合，u轴、v轴分别与对角线B1B3和B2B4重合，w轴垂直于动平台向上。机构在初始位置时，动平台处于水平位置，两坐标系的坐标轴分别对应平行。令OA1=OA2=OA3=OA4=a，PB1=PB2=PB3=PB4=b，连杆CiBi长度为ei，主动移动副位移为li。β、α分别为动平台相对静平台绕定坐标系y轴和绕动坐标系u轴转动的姿态角。

3.1 位姿分析

3.1.1 位姿逆解

对于图1所示机构，其位姿逆解就是给定动平台上点P的位置坐标P=(Px,Py,Pz)及动平台的姿态角α和β，求其各驱动滑块的位移li。

由于该机构中的闭回路A1C1B1B3C3A3可视为平面六杆机构，故动系坐标的原点P沿y轴方向的位移始终为零，因此点P在静坐标系下的位置坐标为(Px, 0,Pz)。令R为动系Puvw相对于静系Oxyz的姿态变换矩阵，则有

(8)

(9)

(10)

式中，Rx′为动平台绕u轴旋转α的变换矩阵；Ry′为动平台绕y轴旋转β的变换矩阵。

若OBi代表Bi点在静坐标系下的坐标，则有

(11)

为了便于建立机构的矢量运动方程，可将图1所示并联机构的结构形式切割为图3、图4所示截面。图3、图4中，mi为滑块移动距离AiCi的单位方向矢量，ni为连杆CiBi的单位方向矢量。根据图3和图4所示支链间的关系，可以写出机构的闭环矢量运动方程：

OP+PBi=OAi+ACi+CiBi

(12)

将相关参数代入式(12)，得

OP+PBi=OAi+limi+eini

(13)

故有

eini=OP+PBi-OAi-limi

(14)

其中，单位方向矢量mi仅与方位角θ有关，且有m1=(cosθ，0，sinθ)，m2=(0，cosθ，sinθ)，m3=(-cosθ，0，sinθ)，m4=(0，-cosθ，sinθ)。

图3 第一和第三支链结构简图

图4 第二和第四支链结构简图

对式(14)取内积，得

(15)

(16)

根据式(16)可求出机构的位姿逆解，即

(17)

式(17)表明机构的位姿逆解有2组，分别对应机构不同的初始装配形式。对于图1所示机构的装配形式，式(17)中的“±”只能取“-”号。当取“+”号时，机构动平台的位于分支中点Ci的下方。

同时，根据式(14)也可得到杆CiBi的瞬时单位方向矢量：

ni=(OP+PBi-limi-OAi)/ei

(18)

3.1.2 位姿正解

已知机构的4个主动移动副的输入位移li，求解动平台的位置坐标(Px，0，Pz)和姿态角α与β。根据图3、图4所示的几何关系和坐标变换矩阵，可建立如下约束方程：

(19)

(20)

(21)

(22)

式(19)～式(22)为机构的位姿方程。这4个方程共同构成了复杂的四元二次非线性方程组，表明该机构具有强运动学耦合性。由于解析法求解普通非线性方程组较为困难，本文采用数值法，通过MATLAB编程和调用solve函数较为简便地对机构进行运动学求解，详见第5节。

3.2 速度分析

将式(13)对时间进行一阶求导，得

(23)

将式(23)等号两端同时右乘ni，得

(24)

根据矢量运算法则可知，(ωi×ni)·ni=0，因此可消去式(24)中最后一项，故有

(25)

进一步把式(25)写成矩阵形式，则有

(26)

C=diag(n1·m1,n2·m2,n3·m3,n4·m4)

式(26)为该并联机构的速度映射方程，其中，ni、PBi×ni、vp、ω均为向量。

将式(23)等号两端同时点乘单位向量mi，可得

(27)

将式(27)进一步可得出中间变量ωi的表达式

(28)

3.3 加速度分析

将式(23)对时间进行一阶求导，得

(29)

将式(29)等号两端同时点乘单位矢量ni，则有

(30)

由式(30)可得

(31)

式(31)即为机构的加速度逆解。

4 结构奇异性

奇异性是并联机构一个重要的内在特性，当并联机构处于奇异位形时，其可控运动范围和静力平衡都会受到影响，因此奇异性分析是并联机构设计中必不可缺少的一环。根据式(26)中矩阵C和D的欠秩形式，可将奇异类型分为逆运动学奇异、正运动学奇异和混合奇异。

4.1 逆运动学奇异

此类奇异发生在矩阵C不满秩、矩阵D满秩的情况下。对于图1所示机构，根据式(26)可知矩阵C为对角阵，因此其对角线上的任意元素满足ni·mi=0时，机构处于逆运动学奇异位形，此时方向单位矢量ni与mi正交。所以该并联机构逆运动学奇异存在的几何条件为，至少一条支链中出现连杆CiBi与移动轨道AiCi相互垂直，如图5所示。在该位形下，即使主动移动副施加一个驱动力，由于机构的传动角为零，动平台也不会产生运动。

图5 逆运动学奇异位形

4.2 正运动学奇异

此类奇异发生在矩阵C满秩，而矩阵D不满秩的情况下。由于式(26)中D为4×6的矩阵，所以其最大线性无关组数为4。当矩阵D不满秩时，其行列式的秩rank(D)<4，并且4个行向量必线性相关，具体情况有以下两种。

(1)当并联机构的4根连杆C1B1、C2B2、C3B3、C4B4相互平行。该位形下4个单位方向矢量n1、n2、n3、n4相互平行，那么矢量PB1×n1、PB2×n2、PB3×n3、PB4×n4必共面，所以矩阵D降秩，即其行列式的秩rank(D)<4，此时机构处于奇异位形，如图6a所示。这种奇异位形同时与机构的结构尺寸相关，一旦动平台的边长小于经平台的边长，即可避免此种奇异位形的产生。

(2)连杆C1B1与连杆C3B3共线，或者连杆C2B2与连杆C4B4共线。这种情况下PBi与ni间的夹角为0°或180°，因此有PBi×ni=0，故矩阵D的第一和第三行线性相关，或者第二和第四行线性相关。这种位形下，矩阵D同样不满秩，即rank(D)<4，所以机构处于奇异位形，如图6b所示。这种奇异位形同样与机构的结构尺寸和主动移动副的运动范围有关，在合适的结构尺寸条件下也可避免此类奇异的发生。

(a)第(1)种情况时的奇异位形

(b)第(2)种情况时的奇异位形

当机构处于正运动学奇异位形时，动平台将“得到”一个或者多个自由度，机构处于不可控状态。

4.3 混合奇异

当发生此类奇异时，矩阵C和D需同时不满秩。根据前面分析可知，若要满足C不满秩，至少一条支链中的连杆CiBi与移动轨道AiCi垂直。D不满秩有两种情况，满足两种情况对应的条件分别为θ=0°和θ=90°。所以当满足C不满秩和D不满秩的任意一种情况的时候，对应的奇异位形如图7所示。可以看出，该并联机构处于一般装配位形下不存在混合奇异。

(a)θ=0°时的机构奇异位形

(b)θ=90°时的机构奇异位形

5 数值算例仿真

为进一步说明利用MATLAB编程调用solve函数进行非线性方程组求解的过程，以t=9 s时得到的滑块位移为初始条件，求得动平台上P点位姿的数值解。此时共得到机构的4组正运动学实数解(表1)，每一组实数解对应其一种装配构型。在给定结构尺寸条件下，根据移动副的输入范围求出机构动平台上点P在z轴方向的运动范围为131.45～180.57 mm，因此可以排除第1和第3组解。而第2组解中，动平台绕y轴的姿态角超β出了球铰的转角范围，也应排除。所以只有第4组解为动平台在此刻的可行位姿。

表1 机构运动学正解计算结果

最后基于所推导出的机构运动学方程，利用MATLAB对机构进行数值仿真和基于虚拟样机的运动学仿真，如图8所示。对比图8中数值仿真和虚拟样机仿真结果可知两者结果完全一致，验证了本文所推导理论公式(包括位姿，速度和加速度)的正确性。

6 结语

本文提出一种新型四自由度2PRS-2PSS并联机构，因其对角分支运动链具有相同的拓扑结构形式，因此该机构具有较好的结构对称性。本文分析了动平台的运动特性，利用矢量法建立了该机构的一般运动学方程。基于所建立的运动学方程，可快速求出方位角θ取不同值时特定装配形式下的机构的运动学解。根据机构速度雅可比矩阵，详细分析了机构的奇异性，并给出了避免奇异位形的相关措施。通过理论编程和虚拟样机仿真，验证了理论分析的正确性和有效性。在后续研究中，我们将讨论和研究主动关节轨道的方位角θ对该机构的工作空间和性能的影响，以便在满足运动性能要求条件下选取机构的最佳装配构型等。同时，在理论分析的基础上进行实体样机研制。

(a)位移曲线 (b)速度曲线

(c)加速度曲线 (d)角位移曲线

(e)角速度曲线 (f)角加速度曲线

[1] 边辉, 刘艳辉, 梁志成, 等. 并联2-RRR/UPRR踝关节康复机器人机构及其运动学[J]. 机器人, 2010(1):6-12. Bian Hui, Liu Yanhui, Liang Zhicheng, et al. A Novel 2-RRR/UPRR Robot Mechanism for Ankle Rehabilitation and Its Kinematics[J]. Robot, 2010 (1): 6-12.

[2] Richard P L, Gosselin C M, Kong X. Kinematic Analysis and Prototyping of a Partially Decoupled 4-DOF 3T1R Parallel Manipulator[J]. Journal of Mechanical Design, 2007, 129(6): 611-616.

[3] 窦玉超, 曾达幸, 李明洋, 等. 一种两转一移完全解耦并联机器人机构及其特性分析[J]. 中国机械工程, 2014, 25(2): 241-245. Dou Yuchao, Zeng Daxing, Li Mingyang, et al. Analysis of a 2T1R Fully Decoupled Parallel Robot Mechanism and Its Characteristics[J]. China Mechanical Engineering, 2014, 25(2): 241-245.

[4] Gan D, Dai J S, Dias J, et al. Singularity-free Workspace Aimed Optimal Design of a 2T2R Parallel Mechanism for Automated Fiber Placement[J]. Journal of Mechanisms and Robotics, 2015, 7(4): 041022.

[5] Clavel R. DELTA, a Fast Robot with Parallel Geometry[C]//Proc. of the 18th International Symposium on Industrial Robots. New York, 1988:91-100.

[6] Gao F, Peng B, Zhao H, et al. A Novel 5-DOF Fully Parallel Kinematic Machine Tool[J]. The International Journal of Advanced Manufacturing Technology, 2006, 31(1/2): 201-207.

[7] Pierrot F, Company O. H4: A New Family of 4-dof Parallel Robots[C]//Proceeding of IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Atlanta, 1999: 508-513.

[8] Song Y, Gao H, Sun T, et al. Kinematic Analysis and Optimal Design of a Novel 1T3R Parallel Manipulator with an Articulated Travelling Plate[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(5): 508-516.

[9] 李永刚 宋轶民, 冯志友, 等. 4自由度非全对称并联机构的完整雅可比矩阵[J]. 机械工程学报, 2007, 43(6): 37-40. Li Yonggang, Song Yimin, Feng Zhiyou, et al. Complete Jacbian Matrix of a Class of Incompletely Symmetrical Parallel Mechanisms with 4-DOF[J]. Journal of Mechanical Engineering, 2007, 43(6): 37-40.

[10] Wang S. The Singularity Research of a Novel 2T2R Parallel Mechanism[C]//The Second International Conference on Mechanic Automation and Control Engineering. Hohhot, 2011: 866-869.

[11] 马履中, 陈修祥, 杨启志, 等. 基于并联机构的具有冗余自由度四自由度弹性阻尼减振装置研究[J]. 中国机械工程, 2006, 17(17): 1761-1764. Ma Lüzhong, Chen Xiuxiang, Yang Qizhi, et al. Research on 4-DOF Parallel Mechanism-Based Vibration Damping Device with Redundant Freedom[J]. China Mechanical Engineering, 2006, 17(17): 1761-1764.

[12] 刘剑敏, 马履中, 许子红, 等. 振动筛两平移两转动并联机构的运动学分析[J]. 农业机械学报, 2008, 39(2): 14-17. Liu Jianmin, Ma Lüzhong, Xu Zihong, et al. Kinematical Analysis of Vibrating Screen on a Kind of 2T-2R Parallel Mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(2): 14-17.

[13] Kumar N, Piccin O, Bayle B. Dimensional Synthesis of a Novel 2T2R Parallel Manipulator for Medical Applications[C]//ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. New York, 2014: V05AT08A069.

[14] 范彩霞, 刘宏昭, 张彦斌. 基于构型演变和李群理论的2T2R型四自由度并联机构型综合[J]. 中国机械工程, 2010, 21(9): 1101-1105. Fan Caixia, Liu Hongzhao, Zhang Yanbin. Type Synthesis of 2T2R 4-DOF Parallel Mechanism Based on Configuration Evolution and Lie Group Theory[J]. China Mechanical Engineering, 2010, 21(9): 1101-1105.

[15] 杨廷力. 机器人机构拓扑结构设计[M]. 北京: 科学出版社, 2012.

(编辑 张 洋)

Design and Kinematics Analysis of a 2PRS-2PSS Parallel Mechanism

Zhang Yanbin Ding Ding Wu Xin Wang Zenghui Zhao Yifu

Henan University of Science and Technology, Luoyang,Henan, 471003

A new two-translational and two-rotational 4-DOF 2PRS-2PSS parallel mechanism was proposed. Orientation angles among axis of all actuated prismatic joints and fixed base of the parallel mechanism were variables. Firstly, the motion output characteristics were analyzed by theory of position and orientation characteristics. The kinematics of the mechanism was analyzed by using vector approach. Forward and inverse solutions of the position and orientation of the mechanism were derived. Then, the equations of velocity and acceleration were obtained. In addition, the singular configurations of the mechanism were discussed in detail based on the singularity of its Jacobian matrices. Finally, simulation results show that the theoretic analysis is correct.

parallel mechanism; degree of freedom(DOF); kinematics analysis; singularity

2016-05-16

国家自然科学基金资助项目(50905055)；河南省高校科技创新团队支持计划资助项目(15IRTSTHN008)；河南科技大学重大科技项目培育基金资助项目(2015XTD012)

TH112；TP242

10.3969/j.issn.1004-132X.2016.21.004

张彦斌，男，1974年生。河南科技大学机电工程学院教授。主要研究方向为机构学与并联机器人理论。发表论文45篇。丁 丁，男，1992年生。河南科技大学机电工程学院硕士研究生。吴 鑫，男，1957年生。河南科技大学机电工程学院教授。王增辉，男，1988年生。河南科技大学机电工程学院硕士研究生。赵浥夫，男，1988年生，河南科技大学机电工程学院硕士研究生。