基于MATLAB的井下压力计电子系统可靠性仿真

闫 建

(重庆三峡职业学院，重庆万州 404155)



基于MATLAB的井下压力计电子系统可靠性仿真

闫 建

(重庆三峡职业学院，重庆万州 404155)

井下压力计是油田压裂作业过程中井下数据的重要测试与储存装置。针对传统可靠性分析周期长、经济性差的局限性，本文运用MATLAB软件编写电子系统仿真软件，很好地解决了这一问题；通过仿真得到井下压力计电子系统的仿真寿命为2877.7小时，并得到电子系统的可靠性曲线和累计失效率曲线；改变电子元器件初始失效率数据，分析得到可靠性曲线和累计失效率曲线的变化趋势，由此推得井下压力计电子系统可靠性的变化规律，这对于工程实践具有重要指导意义。

井下压力计；电子系统；可靠性；仿真

井下压力计是油田压裂增产最为常用的测井仪器，主要测量压裂时井底的温度和压力。井下压力计能否有效地采集数据，直接关系到对压裂效果及开采率的评估。故井下压力计是否能够稳定、可靠地工作就显得非常重要。传统可靠性分析周期长、经济性差，不能满足企业的需求，随着计算机的快速发展，数字仿真的出现创造性地解决了这一难题[1]。本文重点研究了井下压力计电子系统的寿命和相关可靠性曲线的变化规律。

1 建立故障树

井下压力计电子系统失效，主要是由于单片机模块、压力信号采集与处理模块、温度信号采集与处理模块、存储器模块和电池模块故障引起。建立故障树实际上也是对具体失效原因分析的一个总结。由于故障树是以树状图的形式来表达系统失效信息，因此它不仅能表现井下压力计的失效事件，还能表现出各子部件之间功能上的逻辑关系。本文所建立的井下压力计故障树选取“井下压力计失效”作为系统的顶事件，通过具体失效原因分析来展开故障树，如图1所示。

图1中故障树底事件对应元器件的失效特征参数都是由《GJB/Z 299C-2006》中的可靠性预计模型及失效参数计算得来[2]。具体失效率如表1所示。

2 可靠性仿真

2.1 仿真原理

步骤一，依次对故障树最小割集所包含的底事件进行失效时间抽样，获得每个最小割集的失效时间；步骤二，比较最小割集的失效时间，取得它们的极小值，该极小值就是系统失效时间的一个抽样值，这样便完成了一次仿真；步骤三，重复步骤一、步骤二，得到系统失效时间的一个样本，对样本统计分析，得到系统可靠性曲线和寿命[3]。

本文所设计的井下压力计所涉及的元器件只要有其中任何一个失效，系统都会失效，故可以知道本系统的每一个元器件都是一个最小割集。

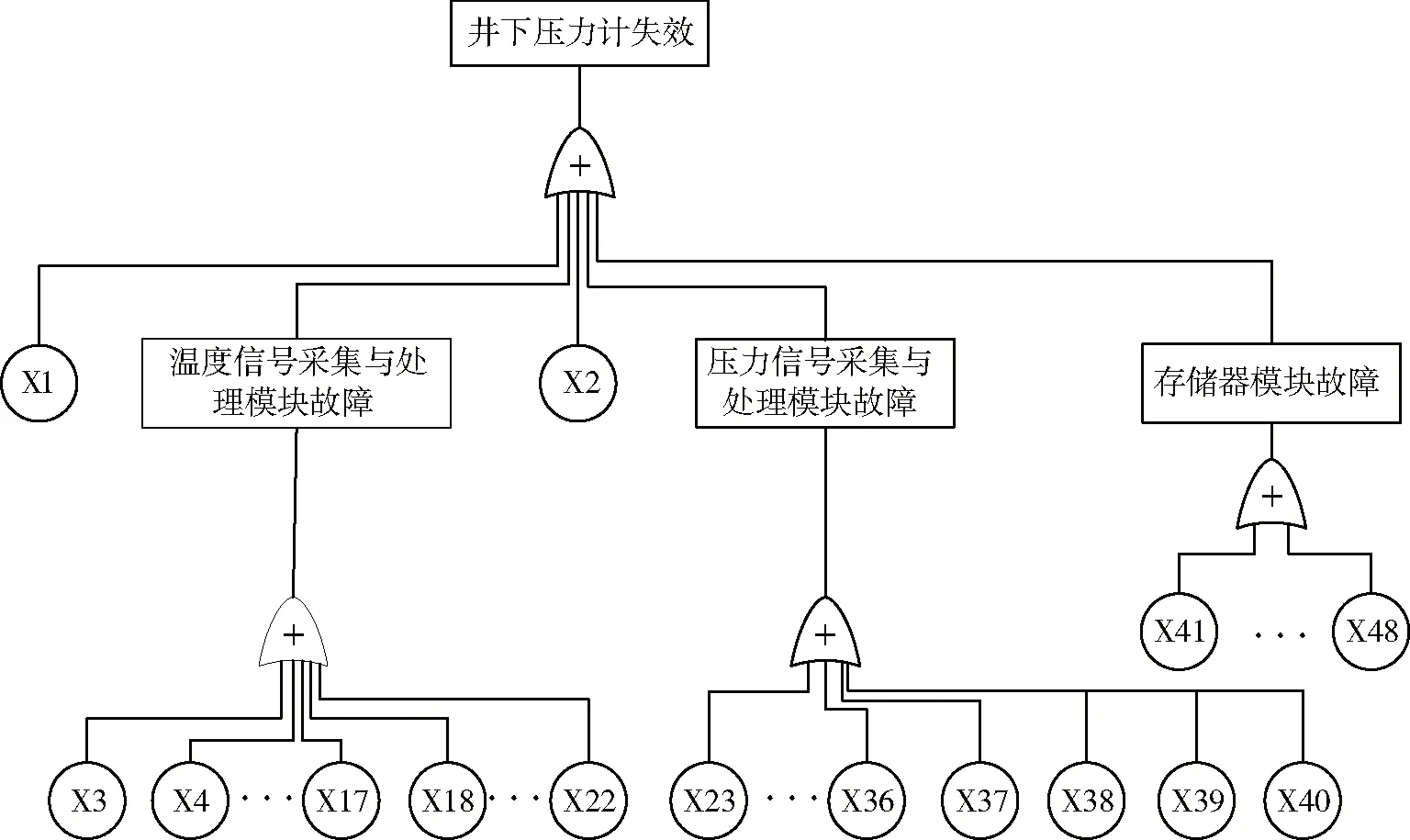
图1 井下压力计电子系统故障树模型

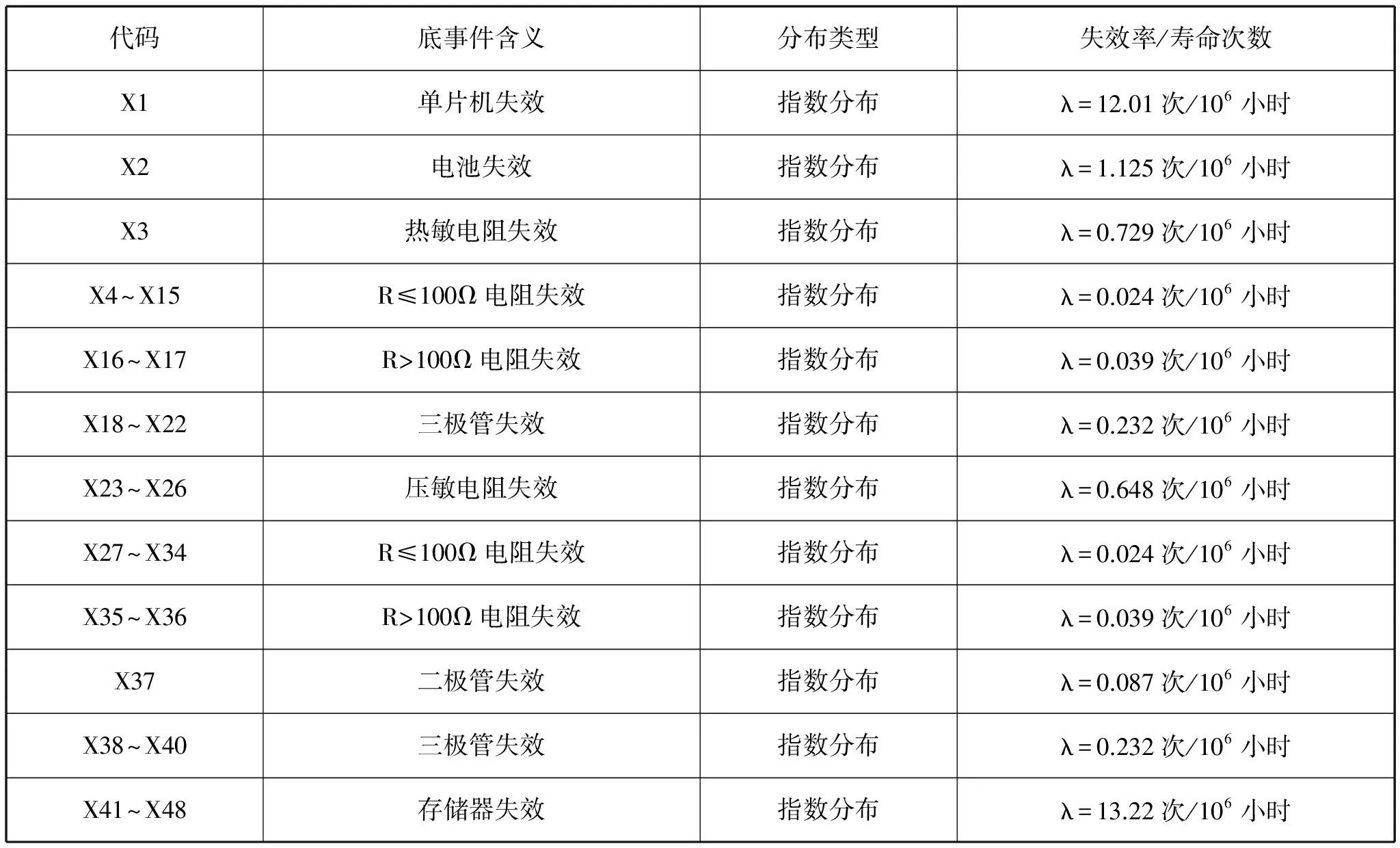
代码底事件含义分布类型失效率/寿命次数X1单片机失效指数分布λ=12．01次/106小时X2电池失效指数分布λ=1．125次/106小时X3热敏电阻失效指数分布λ=0．729次/106小时X4～X15R≤100Ω电阻失效指数分布λ=0．024次/106小时X16～X17R>100Ω电阻失效指数分布λ=0．039次/106小时X18～X22三极管失效指数分布λ=0．232次/106小时X23～X26压敏电阻失效指数分布λ=0．648次/106小时X27～X34R≤100Ω电阻失效指数分布λ=0．024次/106小时X35～X36R>100Ω电阻失效指数分布λ=0．039次/106小时X37二极管失效指数分布λ=0．087次/106小时X38～X40三极管失效指数分布λ=0．232次/106小时X41～X48存储器失效指数分布λ=13．22次/106小时

2.2 编写仿真软件

基于蒙特卡罗理论，利用MATLAB软件编写可靠性仿真软件[4]。仿真软件的算法流程如图2所示。

具体说明如下：

第一，规定系统的最大工作时间为Tmax，将它等分成m个相等的时间间隔。每个时间间隔为ΔT，则有ΔT=Tmax/m。本文中规定Tmax=10000小时。

第二，规定仿真运行的次数N，本文仿真次数N=100000次。

第三，根据建立的故障树模型，该故障树有n个底事件，涉及系统的n个基本元器件。对于第i个基本元器件，其失效分布函数Fi(t)已知。

第四，前面已知第i个基本元器件的失效函数Fi(t)，其反函数就是该基本元器件的失效时间[5]。

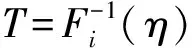
(1)

其中，η为[0,1]区间上均匀分布的随机数。通过该抽样方法可以得到N次仿真系统的寿命矩阵T，该矩阵的维数为N×n，矩阵的每一行即为系统的一次仿真。再利用MATLAB提供的函数，求出每一次仿真的最小失效时间矩阵Ts，该矩阵的维数为N×1。

第五，仿真结束，对失效样本进行统计分析，得到系统的各项可靠性指标。

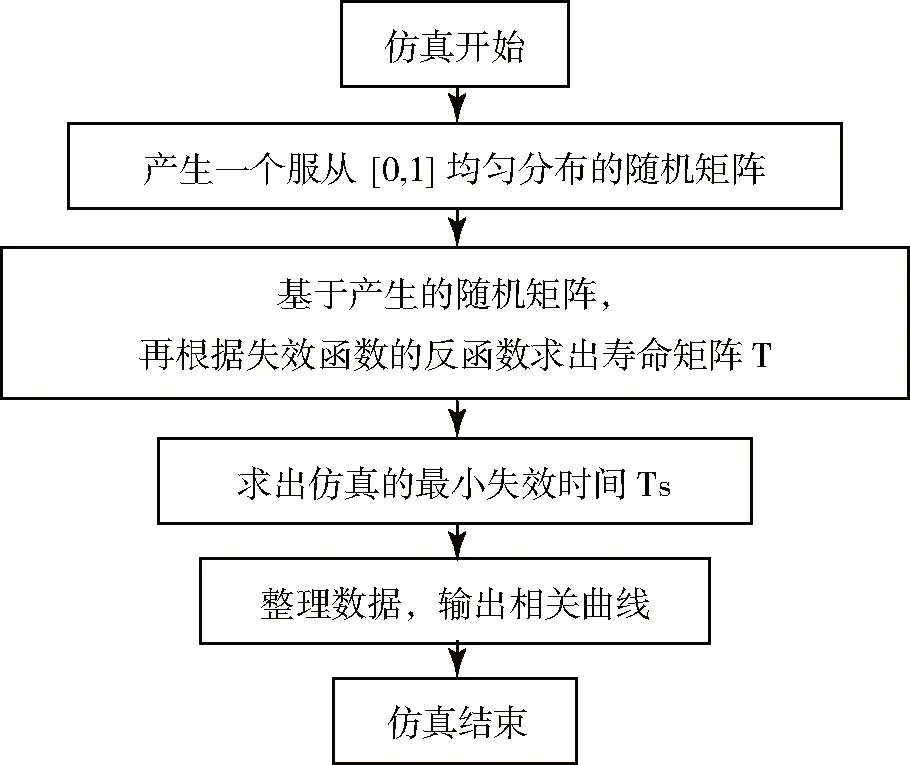
图2 算法流程图

3 仿真结果分析

3.1 累计失效率及变化规律

根据仿真的各项数据，再由公式(2)得到系统的累计失效率(不可靠度)曲线，如图3所示[6]。

Fs(tr)=mr/N.

(2)

图3 累计失效率(不可靠度)曲线

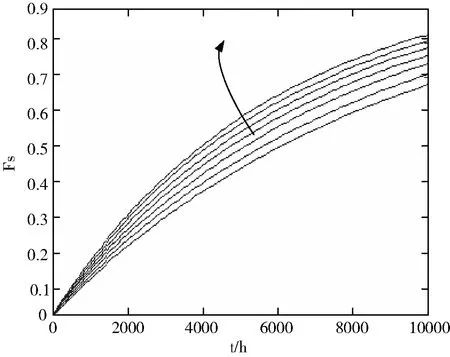
图4 累计失效率系列曲线

在图3中，横轴表示仿真时间，纵轴表示累计失效率。随着时间的增加，累计失效率不断增大，逐渐趋近于1，与实际相符。

在图4中，在其它元器件失效率不变的情况下，沿着箭头方向的7条曲线分别是单片机失效率为1次/106小时，12次/106小时，22次/106小时，32次/106小时，42次/106小时，52次/106小时，62次/106小时的累计失效率系列曲线。随着单片机失效率不断增加，电子系统的累计失效率曲线不断沿着箭头的方向移动，即系统的累计失效率逐渐增大。当其它元器件失效率增加时，有着类似的规律。

3.2 可靠度及变化规律

由仿真数据，根据式(3)可得系统可靠度曲线，如图5所示。

Rs(tr)=1-Fs(tr).

(3)

在图5中，横轴表示仿真时间，纵轴表示可靠度。随着时间的增加，可靠度不断减小，逐渐趋近于0，与实际相符。

在图6中，在其它元器件失效率不变的情况下，沿着箭头方向的7条曲线分别是单片机失效率为1次/106小时，12次/106小时，22次/106小时，32次/106小时，42次/106小时，52次/106小时，62次/106小时的可靠度系列曲线。随着单片机失效率的不断增加，电子系统的可靠度曲线不断沿着箭头的方向移动，即系统的可靠度逐渐减小。当其它元器件失效率增加时，有着类似的规律。

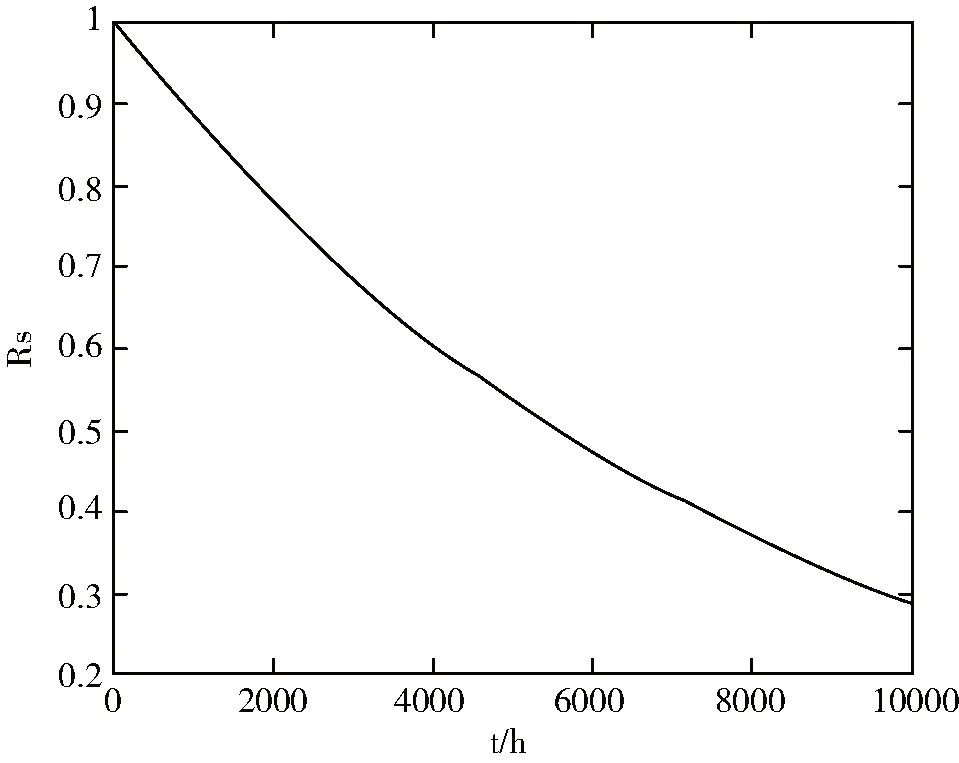
图5 可靠度曲线

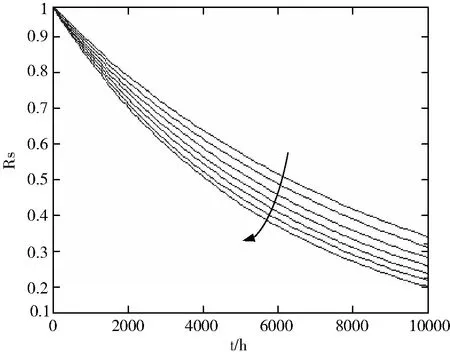
图6 可靠度系列曲线

3.3 系统失效概率分布

由仿真数据，根据式(4)可得系统失效概率分布直方图，如图7所示。

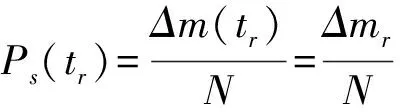
(4)

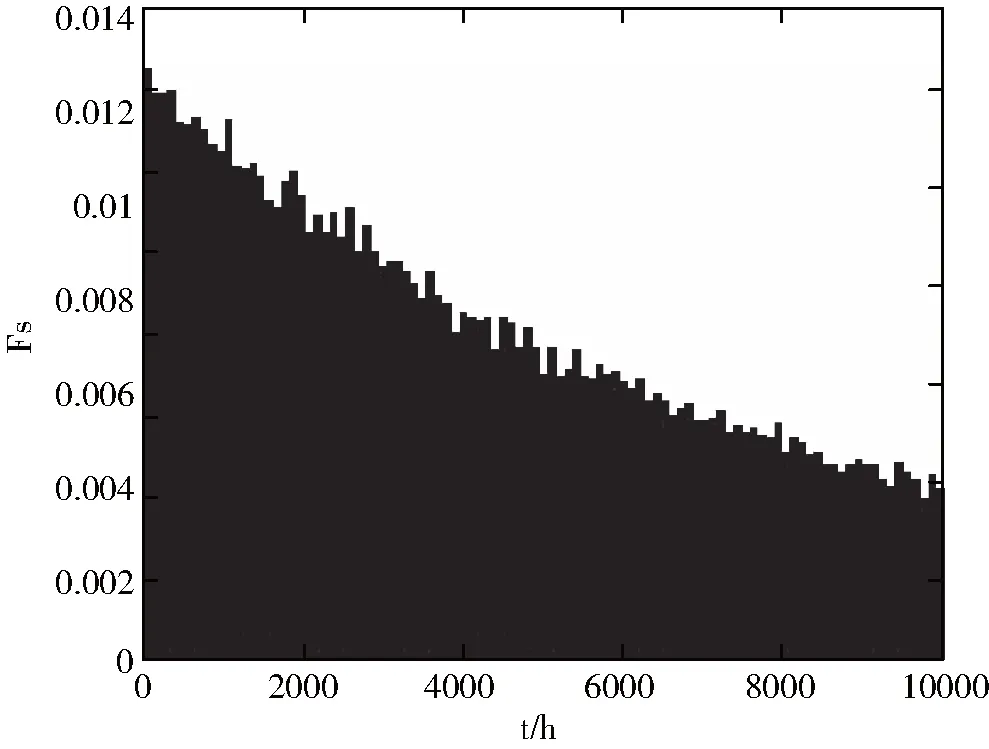
图7 系统失效概率分布直方图

在图7中，用直方图表示了压力计电子系统在寿命的不同时期的失效概率分布以及变化情况。横坐标上每一个直方图的跨距为100小时，纵轴是在仿真过程中失效事件分别落在不同时间区间的概率。电子压力计的失效概率分布直方图也是基本服从指数分布的。这也说明，电子元器件主要以指数分布的形式失效，与理论相符合。

3.4 系统寿命

根据仿真数据，再由公式(5)可以得到系统的寿命。

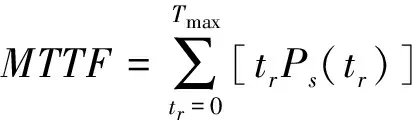
(5)

通过公式(5)处理得到系统平均无故障工作时间为2877.7小时左右。按压力计下到井下后每天24小时计算，可连续工作约120天，完全满足压裂作业对压力计的要求。

4 结论

首先，通过仿真得到井下压力计电子系统的寿命大约为2877.7小时，按压力计下到井下后，每天24小时计算，可连续工作约120天，完全满足压裂作业对压力计的要求。由此也可以得出，电子元器件工艺本身能够满足井下压力计的要求，而井下压力计的失效往往是由于密封失效或者机械振动所导致。

其次，在没有冗余设计的情况下，随着电子元器件失效率的增加，系统累计失效率逐渐增大，系统可靠度逐渐减小，系统寿命逐渐减小。

[1]P.M.Hannah,K.L.Vekved.Precision pressure measurement: the key to accurate Fluid-Interface monitoring [C].SPE Permian Basin Oil and Gas Recovery Conference,21-23March,Midland,Texas, 2000.

[2]曾纪科,韩常英.电子设备可靠性预计手册[M].北京:科学出版社,2006:50-70.

[3]林凤梅.故障树分析及仿真方法在球磨机传动系统中的应用研究[D].保定:华北电力大学,2003.

[4]罗华飞.Matlab GUI学习手记[M].北京:北京航空航天大学出版社,2009:271-302.

[5]石彬.基于故障树的EPS系统可靠性及失效模式仿真研究[D].杭州:浙江大学,2007.

[6]王正林,刘明.精通MATLAB7[M].北京:电子工业出版社,2006:1-224.

Reliability Simulation of Electronic Systems of Downhole Pressure Gauge Based on MATLAB

YAN Jian

(Chongqing Three Gorges Polytechnic College, Wanzhou Chongqing 404155,China)

Downhole pressure gauge is an important test and data storage devices during downhole oilfield fracturing. Aim at the long cycle and poor economic limitations of traditional reliability analysis, this paper solved the problem by writing simulation software used MATLAB.To obtain life of electronic systems of downhole pressure gauge is 2877.7 hours and associated reliability curve.To get the trend of reliability curve by changing the initial failure rate of electronic components,and to get the reliability regulation of electronic systems. It has important guiding significance for engineering practice.

downhole pressure gauge; electronic systems; reliability; simulation

2016-06-23

闫 建(1988- )，男，讲师，硕士研究生，从事机电系统测试传感理论及信息处理研究。

TE319

A

2095-7602(2016)12-0029-05