基于Fluent的高耸塔体风荷载数值模拟

熊凤鸣

（中石化上海工程有限公司，上海 200120）

基于Fluent的高耸塔体风荷载数值模拟

熊凤鸣

（中石化上海工程有限公司，上海 200120）

对某高耸塔体结构表面的风场和风压分布进行了数值模拟和结果分析，湍流模型选择RNG k-ε模型，计算得出塔体周围的流场分布和结构上各个测点的风压。分析塔体在风向角变化时的风荷载分布特征，对比各风向角下截面风压分布的模拟结果和规范体型系数数据，探讨其取值问题，为此类结构的抗风研究与设计提供依据，对石油化工项目中料仓等大型塔体以及钢储罐等风敏感结构的风荷载分析也有一定的借鉴意义。

数值模拟；高耸塔体；风压系数；体型系数

造粒塔是石油化工装置中常见的一种构筑物，具有明显的高度高、横截面尺寸相对小等高耸结构的特点，相对于竖向荷载而言，风荷载的横向作用影响较大，往往是其控制荷载。

由于造粒塔的截面形式是圆形与矩形截面的组合截面形式，其风荷载计算的取值在《建筑结构荷载规范》（GB 50009—2012）中仅给出了圆截面局部计算时表面分布的体型系数以及单一矩形截面的风荷载体型系数，无法对实际组合截面的风荷载有一个更为准确的取值。

目前对结构表面风压除采用风洞试验方法获得以外，计算流体动力学（CFD）由于其低成本、快速度、实尺建模[1]的优势，在结构风工程领域日益广泛被应用于复杂结构的风荷载研究[2-4]。鉴于以上基础，本文结合工程实际以CFD 数值模拟方法对具有复杂体形的高耸塔体结构进行了数值模拟和分析，对规范体型系数数据取值进行探讨，为此类结构的抗风研究与设计提供参考，对石油化工项目中料仓等大型塔体以及钢储罐等风敏感结构的风荷载分析也有一定的借鉴意义。

1 模型选择和处理

1.1 湍流模型

标准k-ε模型、 改进的RNG k-ε模型和Realizable k-ε模型，是目前CFD工程中应用最广泛的湍流模型。其中，RNG k-ε模型可以更好地处理高应变率及流线弯曲程度较大的流动而被广泛用于各种结构类型的流动模拟[5]。因此本文选择RNG k-ε湍流模型进行计算，得到了较为理想的结果。

1.2 近壁面的处理

流体的湍流流动在近壁面处会受到十分显著的影响，其处理方法对数值模拟结果的准确性有着较大的影响。而RNG k-ε湍流模型对处理湍流的核心区域有较好的适应性，本文采用非平衡壁面函数法（non-equilibrium wall functions）处理近壁面的湍流状态，以此来修正RNG k-ε湍流模型的计算。

2 计算实例

2.1 工程背景

作为一个计算实例，考虑某造粒塔结构，塔体总高度为84 m，主体为外径12 m的圆筒形，楼电梯间附着于塔体一侧，其横截面尺寸如图1所示。为进行对比，本文考虑塔体不开洞的情况。该塔所处地为B 类地貌，50 年一遇的基本风压为0.45 kN/m2。

2.2 CFD模拟计算

（1）建立模型

为使计算域的设置基本不影响计算结果，需使计算域的边界离物体足够远，使边界对研究对象的影响忽略不计。这可以通过控制研究对象在流场中的布置位置和阻塞率[6]（ 建筑物最大迎风面积与计算域横截面面积的比值）这一指标不大于3 %来实现。

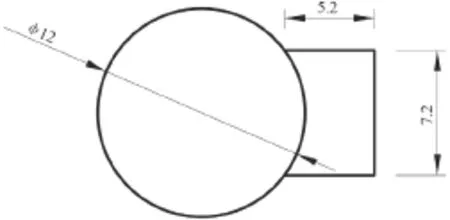
图1 造粒塔横截面尺寸Fig.1 The cross section size of the prilling tower

为使模拟区的流场为充分发展流场，参考相关文献[7～9]，本文对于本塔体实际情况采用1∶1比例实尺建模，如图2所示；计算区域大小取240 m×960 m×480 m（宽×长×高），研究对象塔体布置于距流场入口1/3流场长度处，阻塞率为1.167 %，满足阻塞率小于3 %的要求，如图3所示。

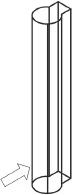
图2 计算模型Fig.2 Computational model

（2）划分网格

本文对计算区域的离散采用非结构化非均匀网格进行划分（如图4所示），为使网格较为平滑，对塔体近壁区和近地面的区域进行适当加密，在其他区域的网格逐渐稀疏。

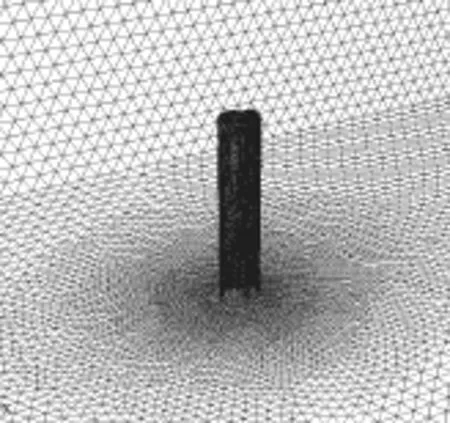
图4 计算区域离散网格Fig.4 Geometric mesh of computational domain

定义来流风向角从0°按逆时针方向增加，各工况如图5所示。

图5 塔体来流风向角Fig.5 Incoming flow direction of tower

（3）边界条件的设定

来流入口边界条件采用速度入口，模拟大气边界层风速剖面分布。来流速度根据我国荷载规范取常用的指数风剖面，即入流面处的速度分量为：

其中：v (z)为高度z处的平均风速；v0为离地面z0= 10 m高度处，50年重现期，10 min的平均风速，由基本风压0.45 kN/m2换算得到v0为26.833 m/s；α为与地面粗糙度有关的指数，本文为B类地区，取α＝0.15。

来流湍流特性通过直接给定湍流动能k和湍流耗散ε值的方式给出：

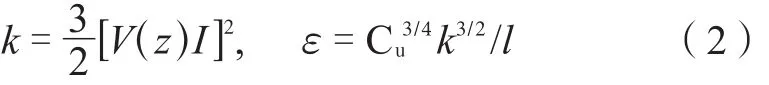
其中，I和l为湍流强度和湍流积分尺度，Cu为常数，取0.084 5。入口和出口处的湍动能和湍能耗散率均按此式计算，当z≤5 m时，取I = 0.23；当5 ＜z≤350 m时，取I = 0.1 ( z / 350 )-α-0.05；当z ＞350 m时，取I = 0.1；l = 100/ ( z /30 )0.5。入口处风剖面v ( z )、k和ε均通过用户自定义函数导入。

出口边界条件采用压力出口；两侧面和上空面均采用对称边界条件，相当于自由滑移的壁面；底面和塔体表面采用无滑移壁面，壁面的粗糙高度，对于地面设置为0.024 m，对于塔体表面设置为0.002 m。

（4）求解和收敛控制

为保证计算过程的稳定性，采用一阶迎风格式来离散化处理方程。采用SIMPLE算法求解压力与速度相关的控制方程组。监测控制方程迭代余量及研究对象表面的风压系数变化，当所有的相对迭代余量均小于5×10-4，且各表面风压系数基本不再发生变化时，认为此时流场进入稳态，迭代收敛。

3 计算结果分析

3.1 风压系数与体型系数

研究对象表面的无量纲的风压力系数CPi定义为：

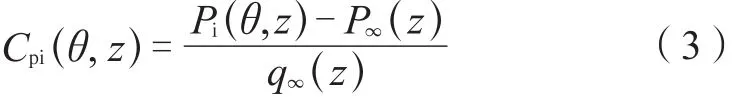
其中，Pi( θ, z)是纬向角θ（塔体测点沿圆周与来流风向的角度，示于图6中）和高度z处风压值（Pa），P∞( z )和q∞( z )分别为高度z处无穷远的来流静压和来流动压，q∞( z ) =1/2 ρvG2，ρ是空气质量密度（kg / m3），vG为参考高度的平均风速（m/s），本文取塔体高度为参考高度，zG= 84 m，塔体高度处平均风速作为参考风速，vG= 36.924 m/s。风压系数Cpi( θ, z)为负值表明此位置为吸力，反之为压力。

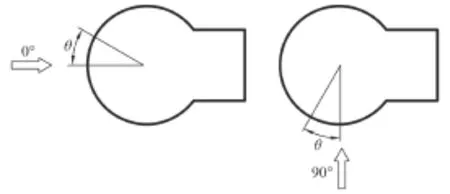
图6 塔体截面的纬向角Fig. 6 Weft angle of the tower section

相应高度处的各点风荷载体型系数，由下式可以得到：

3.2 塔在典型风向角下的体型系数结果分析

在《建筑结构荷载规范》中给出了圆截面局部计算时表面分布的体型系数μs，在《尿素造粒塔设计规定》（HG/T 20672—2005）中给出了塔体风荷载体型系数的计算公式：

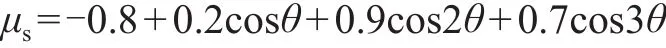
式中：θ为纬向角，如图7所示。

图7 尿素造粒塔设计规定塔体风荷载体型系数Fig. 7 Wind load shape coefficient of specification

工程中通常取Z / H 在 0.4 ～ 0.8高度之间的风压系数来研究。本文取63 m高度处，即3/4 H处风压系数换算的体型系数来进行对比。为分析方便，对塔体表面进行分区，如图8所示。

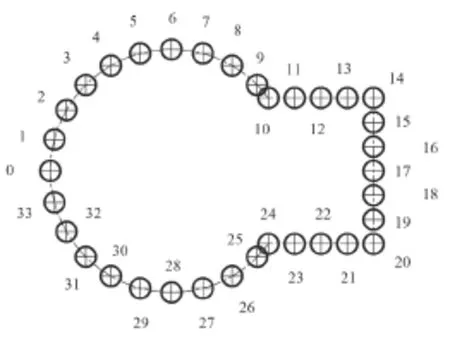
图8 塔体区位编号Fig. 8 Location number of tower section

（1）0°风向角下的体型系数分析

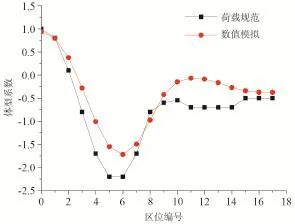
图9 塔体在0°风向角下模拟结果与荷载规范数据的比较Fig.9 The comparation between simulation results and data calculated from load code under the 0° incoming flow

用CFD方法计算塔体在实际尺寸情况下的体型系数，图9给出在0°风向角下塔体63 m高度处各区位（因结构关于流场对称，只取编号0-17对应的区域）的体型系数变化曲线，并与荷载规范中圆截面和矩形截面计算出的数据进行比较。

由图9可知，CFD模拟的塔体体型系数在编号0-10区域范围内与圆截面的数据比较接近，且均在荷载规范的数据包络线内，说明数值模拟的结果可信度较高；而矩形截面的体型系数相差较大，这主要有两方面的原因：① 矩形截面的封闭式房屋和构筑物相对来讲体型变化不大，风压分布较为均匀，荷载规范仅列出了其整体体型系数，这里采用的数据点均为矩形截面侧风向和背风向的整体体型系数，亦即其平面体型系数的面积加权平均，对于数值模拟的结果采用的是局部体型系数，反映了截面上具体的风压分布；② 上述荷载规范给出的矩形截面侧风向和背风向的整体体型系数反映的是简单的单一矩形截面的风压分布情况，而这里由于塔体采用的组合截面，其实际风压分布必然不同，编号11-14的塔体区域的体型系数为负压，且绝对值呈增大的趋势，这是由于风在圆截面绕流的时候，在编号10的位置塔体截面发生了突变，圆柱绕流受到了矩形截面侧向的阻挡，改变了前进的方向。所以在编号10的位置附近，体型系数在短暂保持逐渐向0逼进的趋势之后，随着风的前行，在编号11的位置附近圆柱绕流迅速发展成紧贴壁面的流动，从而形成了负压，并且绝对值逐渐增大。对于编号14-17的区域与荷载规范中矩形截面的风压分布规律无异，绝对值偏小。此趋势比较体现了用数值模拟的方法探寻实尺模型在风场中的压力分布规律的意义所在。

图10给出塔体63 m高度处的体型系数与尿素造粒塔设计规定中数据的比较。可以发现，除了在编号7、8附近数值模拟的结果绝对值略大以外，两组数据在编号0-10区域范围内基本一致，在编号10-17区域规律同图9。

（2）90° 风向角下的体型系数分析

图11给出在90°风向角下塔体63 m高度处各区位（因结构关于流场非对称，取编号0-33对应的区域）的体型系数变化曲线，并与荷载规范中圆截面和矩形截面计算出的数据进行比较。

图10 塔体在0°风向角下模拟结果与造粒塔规范数据的比较Fig.10 The comparation between simulation results and data calculated from prilling tower specification under the 0° incoming flow

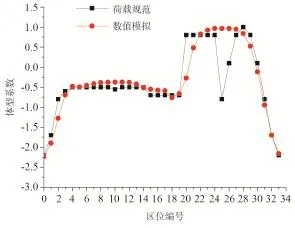
图11 塔体在90°风向角下模拟结果与荷载规范数据的比较Fig.11 The comparation between simulation results and data calculated from load code under the 90° incoming flow

由图可知，CFD模拟的塔体体型系数基本上都与荷载规范的数据相差不大，趋势也大体相同，仅在编号24-27的区域范围内与所采用荷载规范的数据有明显的不同。其中数值模拟的结果显示这部分区域受到的风压为正，体型系数均在接近于1的水平，而所取荷载规范的数据却在-0.8 ～ 0.8之间变化，这主要是因为：此区域所采用的荷载规范数据是单个圆截面的局部体型系数，而实际上，来流受到具有组合截面的塔体阻挡，在塔体迎风面长度的一半位置即编号26的位置附近发生了左右分离，导致塔体24-27区域内受到的风压均为正。所以在24-27区域内不能简单地采用荷载规范中单一圆截面的体型系数，而应根据实际情况进行取值，在进行风洞试验不太现实的情况下，数值模拟就显现出了它的优越性。

图12给出塔体63 m高度处的体型系数与尿素造粒塔设计规定中数据的比较。可以发现，其规律基本同图11。但是在编号0-4的区域附近，荷载规范体型系数的绝对值比造粒塔规范的要大，且数值模拟的结果与荷载规范给出的数据吻合较好，建议在90°风向角实际取值时，此位置区域按荷载规范给出的数据进行选取。

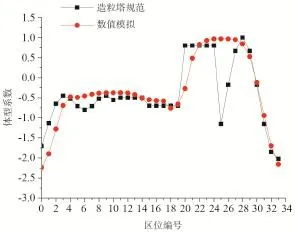
图12 塔体在90°风向角下模拟结果与造粒塔规范数据的比较Fig.12 The comparation between simulation results and data calculated from prilling tower specification under the 90° incoming flow

（3）180° 风向角下的体型系数分析

图13、图14给出在180°风向角下塔体63 m高度处各区位（取编号0-17对应的区域）的体型系数变化曲线，并与荷载规范中圆截面和矩形截面计算出的数据进行比较。从图中可以看出，CFD模拟的塔体体型系数与两规范的数据曲线趋势基本相同，在编号6-10的区域范围内，数值模拟的结果要比规范给出的数据绝对值要小，这是由于来流在塔体编号14的位置发生了明显的分离，在编号14-10的区域附近产生了旋涡，导致塔体6-10区域内流速较小，相应地降低了其体型系数。

另外，我们可以得出：① 规范数据是从风洞试验和实测中得出，或者是在此基础上进行了一定的曲线拟合，与真实情况必然存在差别；② 塔体表面实际的粗糙度与CFD中所设定的有所差别，会导致分离点的不同；③ CFD理论中的一些湍流模型参数是经验值，在具体工程应用中还需结合实际情况进一步验证和改进；④ 边界条件设置的准确性以及网格划分的疏密程度会对模拟结果产生一些影响。⑤ 本文取3/4 H处风压系数换算的体型系数来进行对比，与其他高度处的体型系数在绝对值上也有一些差别。综上，数值模拟的结果与规范数据会有一定的差别，但是对于反映其实际分布规律可以说是没有影响的。

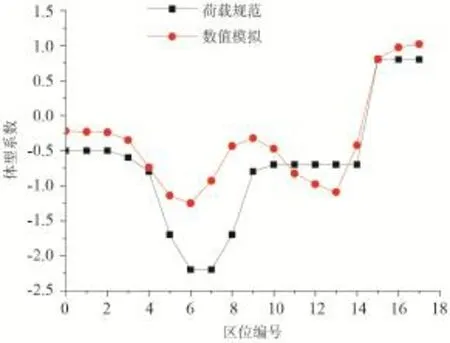
图13 塔体在180°风向角下模拟结果与荷载规范数据的比较Fig.13 The comparation between simulation results and data calculated from load code under the 180° incoming flow

图14 塔体在180°风向角下模拟结果与造粒塔规范数据的比较Fig.14 The comparation between simulation results and data calculated from prilling tower specification under the 180° incoming flow

4 结论

（1）数值模拟的结果可信度较高，计算结果有一定的借鉴意义。

（2）在编号0-4的区域附近，建议在90°风向角实际取值时，此位置区域按荷载规范给出的数据进行选取。

（3）对于具有组合截面的结构，不能完全简单地分别采用规范中单一截面的体型系数，而应根据风洞试验或数值模拟的结果进行取值。

参考文献

[1]帕坦卡著，张政译. 传热与流体流动的数值计算[M]. 北京：科学出版社，1984. 4-6.

[2]郑德乾，等. 世博轴膜面平均风压的数值模拟研究 [J]. 建筑结构学报，2009，30（05）：212-219.

[3]张敏，等. 群体高层建筑风荷载干扰效应的数值研究 [J]. 工程力学，2008，25（01）：179-185.

[4]杨立国，等. 错列超高层建筑群风荷载静力干扰效应的试验与数值模拟研究 [J].建筑结构，2011（11）：125-130.

[5]王福军. 计算流体动力学分析[M]. 北京：清华大学出版社，2004.

[6]杨伟.基于Rans的结构风荷载和响应的数值模拟研究[D].上海：同济大学，2004.

[7]梁向丽.高层建筑周围风场研究[D].武汉：武汉科技大学，2004.

[8]陈文烈.复杂高层建筑风特性及相互干扰的数值模拟[D].杭州：浙江大学，2006.

[9]傅小坚.双塔高层建筑风荷载干扰效应的数值模拟研究[D].杭州：浙江大学，2007.

Numerical Simulation of Wind Load Acting on High Tower by Using Fluent

Xiong Fengming
（SINOPEC Shanghai Engineering Co., Ltd, Shanghai 200120）

In this article, numerical simulation and analysis for wind field and wind pressure around high tower was carried out. RNG k-ε model was selected as turbulent flow model. The distribution of flow around the tower and wind pressure at each measuring point were calculated. The feature of wind load distribution when wind direction angle was changed was analyzed. The simulation results and the shape coefficients in code were compared. The values of these coefficients were then discussed so that the basis of windresistant study and design for high tower was provided, which can be used as reference in design of large vertical equipment, such as silo and steel storage tank.

numerical simulation; high tower; wind pressure coefficient; shape coefficient

TQ 053.5

A

2095-817X（2016）06-0018-006

2016-08-15

熊凤鸣（1983—），男，工程师，主要从事石油化工项目设计、管理工作。