水平定向穿越钢管回拖力的分析与实测

李素贞, 李 翔

(1.同济大学 建筑工程系,上海200092；2.同济大学 土木工程防灾国家重点实验室,上海200092)



水平定向穿越钢管回拖力的分析与实测

李素贞1,2, 李 翔1

(1.同济大学 建筑工程系,上海200092；2.同济大学 土木工程防灾国家重点实验室,上海200092)

为了保证水平定向穿越的顺利实施,回拖力的确定至关重要.总结国内外管道回拖力计算的规范方法,针对主要区别的泥浆阻力及管道弯曲大变形阻力两部分,建立泥浆阻力模型和管道弯曲大变形阻力模型,形成更精细的回拖力计算公式,分析水平定向穿越回拖全过程的管道受力.对比某实际天然气管线工程整个回拖过程的施工监测结果表明,提出的回拖力计算方法与实际情况更吻合,管道弯曲大变形阻力占回拖力的主要部分,回拖力随管线大转角处拐角的增加呈指数增长.

水平定向穿越；回拖力；泥浆阻力；管道弯曲大变形；施工监测

城市建设经常伴随着地下管线的建设、维修或更换.与传统的开挖施工比较,管道非开挖技术对地面干扰小、综合成本低[1].目前大约有41.6%的市政管道修复工程指定采用非开挖技术.水平定向穿越在不到50 a的发展历史中,以环保、效率高的特点在世界各地得到广泛应用,在各种非开挖施工方法中所占的比例达到70.2%.到2013年底,国内水平定向钻机的保有量已达13 030台,在城市化建设中发挥了重要作用[2].

水平定向钻进技术是以水平定向钻机为主安装管道的一种技术,施工过程一般可以分为3个阶段,即钻先导孔、扩孔和管道回拖[3-4].管道回拖作为穿越过程中最关键的一步,由于施工过程的不可预见性,与之相关的回拖力计算成为首要解决的问题.穿越管道在回拖过程中的受力非常复杂,目前普遍认为主要受到以下5种阻力[3]：1)穿越管道与孔壁间的摩擦阻力；2)管道与地表之间的摩擦阻力；3)绞盘效应力,源于沿弯曲钻孔轨迹拖拉管道产生的递增承载压力；4)流体阻力；5)弯曲时由管道刚度产生的阻力.回拖力的计算涉及土力学、工程力学、流体力学、弹性力学等方面的知识,与工程实际的地质环境、穿越轨迹等密切相关[5-6].在实际工程中,由于考虑的孔内受力条件不同,回拖力的计算公式有多种.

我国《油气输送管道穿越工程施工规范》[7](GB 50424-2007)提出适用于油气输送管道的回拖力计算公式,《给水排水管道工程施工及验收规范》[8](GB 50268-2008)提出针对于城镇公用设施管道的回拖力计算公式.美国材料与实验协会法(American Society for Testing and Materials,ASTM)以绞盘法为基础,提出简单、实用的ASTM法[9]；Huey等[10]为定向钻安装钢管提出回拖力计算方法,称为国际管道研究协会(Pipeline Research Council International,PRCI)的计算方法.一些国内学者提出卸荷拱土压力计算法[5]和净浮力计算法[5].Phillps Driscopipe给出计算聚乙烯管回拖力的计算公式[11],Polak等[12]对回拖力各组成部分建立模型,给出相应的回拖力计算公式,在此基础上,Polak等[13]提出聚乙烯管在HDD施工过程中的回拖力计算理论模型以及Cheng等[14]确定了在HDD施工过程中,管道位于16种几何形状下的回拖力计算理论模型.

比较国内外规范以及相关学者的研究工作发现,各种回拖力计算方法的主要差异在于泥浆流体阻力和管道弯曲大变形产生的阻力两部分的分析.针对回拖管道的实际受力情况,笔者在前期工作中确立更精细的泥浆阻力模型和管道弯曲大变形阻力模型[15-16].本文引入这两类阻力模型建立相应的回拖力计算公式,分析水平定向穿越管道回拖全过程的受力.结合某实际工程水平定向穿越的监测结果,比较各种规范方法和本文方法的计算精度.

1 油气管道回拖力计算规范方法

1.1 《油气输送管道穿越工程施工规范》

《油气输送管道穿越工程施工规范》(GB 5040424-2007)适用于油气输送管道在陆上穿越人工或天然障碍的新建或扩建工程.回拖力计算公式主要考虑了穿越管道与孔壁之间的摩擦阻力和泥浆对管道的黏阻力.

(1)

式中：Ft为计算的拉力,L2为穿越管道的长度,f为摩擦系数,D为管子的直径,ρ1为泥浆的密度,δ1为管子的壁厚,kf为黏滞系数.

1.2 国际管道研究协会(PRCI)的计算方法

国际管道研究协会的计算方法是由Huey等[10]在1996年为定向钻安装钢管道而提出的.该方法考虑了管土之间的摩擦阻力、泥浆的黏阻力、重力和弯曲变形阻力的影响,但没有考虑管道拖入孔道之前与地表面的摩擦阻力,并认为管道进入钻孔时的回拖力为零,最大回拖力出现在回拖最后阶段并以递增的方法沿管道分布.该方法将整个管道分解为许多直线段和曲线段,最后的轴向拉力为每小段拉力的总和.

直线段拉力的计算公式为

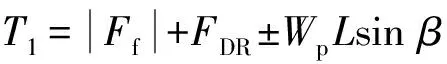
(2)

Ff=μbWpLcosβ.

(3)

式中：T1为直线段拉力,Ff为孔道内摩擦阻力,FDR为DRAG孔液的阻力，μb为管道与孔壁的摩擦系数,Wp为考虑钻孔液浮力后管道单位长度的净重,L为直线段管道长度,β为管道倾角.

DRAG孔液的阻力为

FDR=πDLμmud.

(4)

式中：μmud为流体阻力系数,D为管道的直径.

弯曲段拉力的计算公式为

(5)

Ff=μbWpLarccosβ.

(6)

式中：T2为弯曲度拉力,Larc为管道弧线长度. 总的轴向拉力为各段拉力之和:

(7)

式中：Ti为第i段管道上的轴向拉力,Ttot为总的轴向拉力.

2 两大阻力模型

针对各种回拖力分析方法中存在较大差异的泥浆流体阻力和管道弯曲大变形阻力,前期工作分别确立了两大计算模型[15-16],简介如下.

2.1 泥浆阻力模型

将泥浆流动模型简化成幂律流体在同心环形空间中的稳定流动,得出管道外表面处泥浆的切应力[15]：

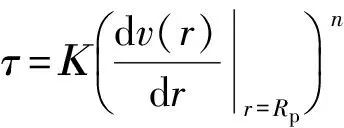
(8)

式中：τ为管道外表面泥浆的切应力,Κ为稠度系数,v(r)为流体流速,n为流体特性指数,v为管道外泥浆至管道中心的距离,Rp为管道外半径.

单位长度上管道外表面上受到的流体阻力为

fd=2πRp·τ.

(9)

式中：fd为单位长度上管道外表面受到的流体阻力.

2.2 管道弯曲大变形阻力模型

在管道通过拐角处后,可以将管道在拐角处的受力情况简化成图1所示[16].

图1 管道拐角处的受力Fig.1 Forces on pipe in corner

AC方向上的力平衡方程为

T2cosψ=(T1+2Rμb)cosψ+2Pμb+NTμb.

(10)

垂直于AC方向上的力平衡方程为

NT=(T1+T2)sinψ.

(11)

由式(10)、(11)可得

(12)

或

ΔT=T1×C1(ψ)+P×C2(ψ).

(13)

式中：P为土体对管道施加的力,

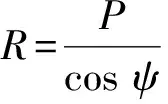
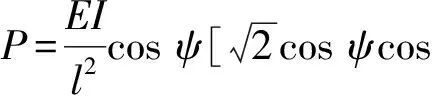
Φ(p,φ0)=0.847 2+F(p,φ0)-2E(p,φ0),

F(p,φ0) 称为第一类椭圆积分,E(p,φ0) 称为第二类椭圆积分.

3 回拖力计算

将实际的管道路线进行简化,得到如图2所示的模型图.

图2 管道路线模型Fig.2 Model for geometry of bore-path

3.1 孔道外管道自重引起的阻力

(14)

或

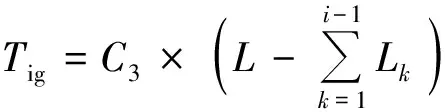
(15)

式中：Tig为孔道外管道自重引起的阻力,ωp为管道自重,μg为管道与地表面的摩擦系数,L为管道总长,Lk为管道第k段长度.

3.2 孔道内管道自重引起的阻力

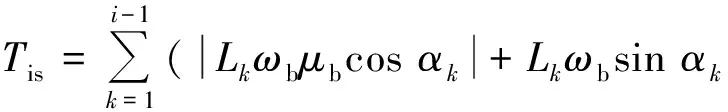
(16)

式中：Tis为孔道内管道自重引起的阻力,ωb为管道在钻液中的自重,αk为管道第k段与水平面的夹角.

3.3 泥浆阻力

根据2.1节建立的泥浆阻力模型,可以得出管道在泥浆中受到的泥浆阻力：

(17)

式中：Tid为泥浆阻力所导致的拉力,fd为单位长度上管道外表面上受到的流体阻力.

3.4 拐角处管道弯曲大变形引起的阻力

当管道到达点2 时,T2f由1点处管道的路线方向改变和弯曲刚度组成,

T2f=T12×C1(ψ1)+P1×C2(ψ1).

(18)

式中：T12=(L-L1)×C3.

当管道到达点3时,T3f由1、2点处的管道路线改变和弯曲刚度组成,T3f=T13f+T23f,

T13f=T13×C1(ψ2)+P1×C2(ψ2),

(19)

T23f=T23×C1(ψ2)+P2×C2(ψ2).

(20)

式中：T13=(L-L1-L2)×C3，T23=T3g+T2s+T2d+T13f.

同理,当管道到达4,5,……点时均可迭代计算出来.式(18)～(20)中,Tif为管道到达点i时,点i处管道弯曲大变形引起的阻力；Tji为当管道到达点i时,点j处管道的轴向拉力；Tjif为当管道到达点i时,点j处管道弯曲大变形引起的阻力.

3.5 总的回拖力

在点i处的回拖力为

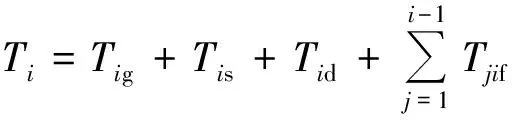
(21)

式中：Ti为管道到达点i时,管道回拖所需要的拉力.

4 实例计算

结合某实际管道工程的水平定向穿越施工监测,比较各种回拖力计算方法的结果.穿越处地质为淤泥质粉质黏土、淤泥质黏土以及流砂土.穿越管道为高频直缝电阻焊钢管(SS400)D325x8,最大穿越设计深度为21.4 m,管道穿越长度为520 m,选用的钻机型号为DDW1200型拖车式定向钻机.在穿越管道前焊接同种材质和大小的4 m测试管道,在测试管道圆周上下、左右对称布置FBG光纤传感器.如图3所示,测得整个穿越过程中的应变,并在管道内布置陀螺仪,实时测试管道在回拖过程中的位置信息.整个施工监测方案如图4所示.测试过程与结果详见文献[17].

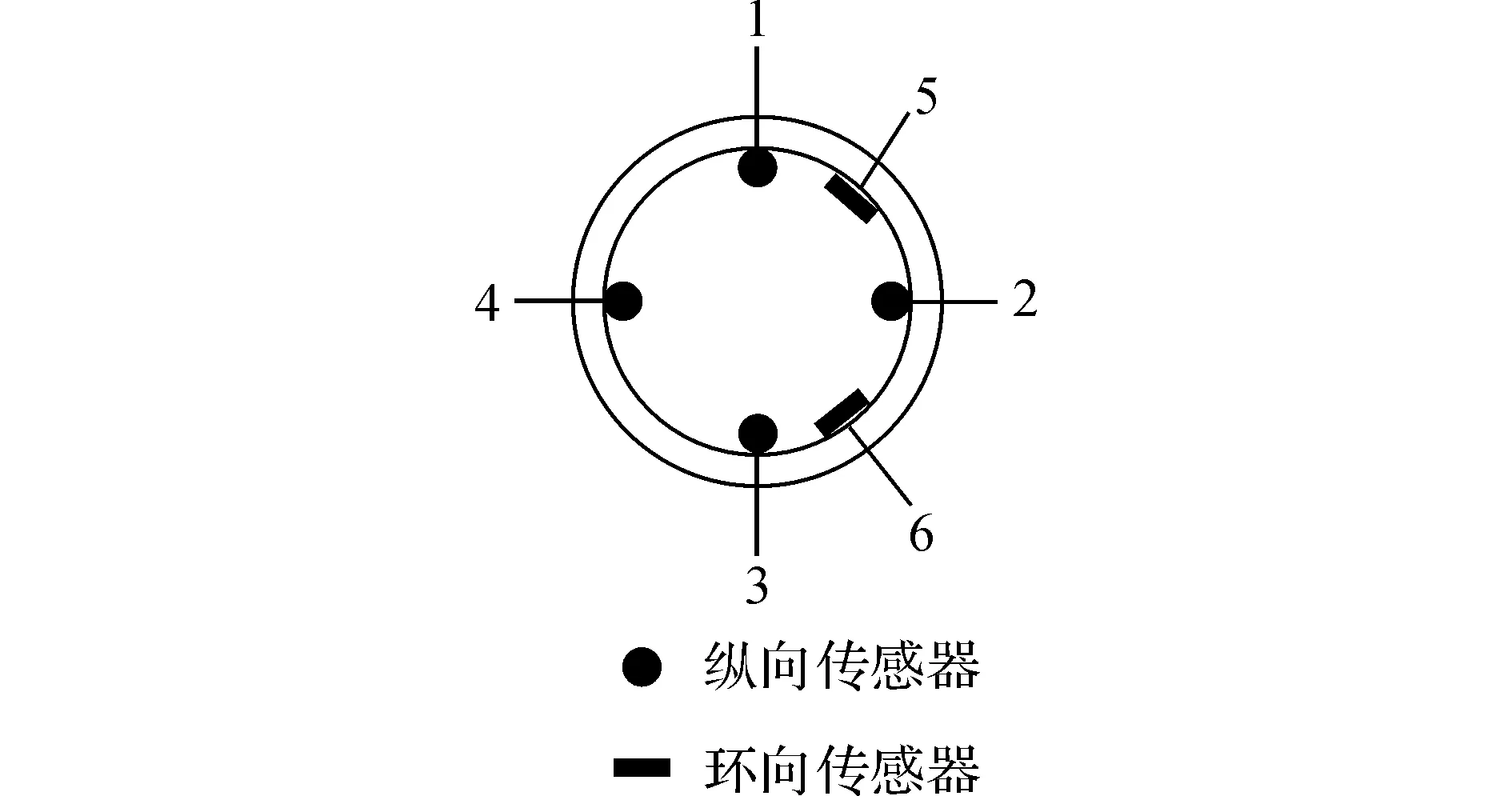
图3 光纤传感器的布置Fig.3 Sensor placement

图4 HDD施工监测方案[17]Fig.4 Scheme for HDD construction monitoring

图5 管道截面图[17]Fig.5 Cross section of pipe

如图5所示，通过管道上传感器布置的位置及应变数据，得出测试管道的轴力和弯矩的计算公式如下：

(22)

和

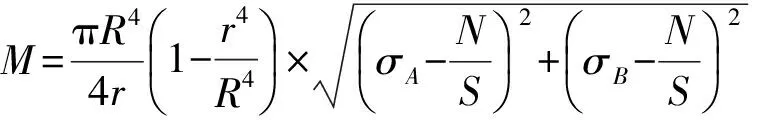
(23)

式中：N为测试管道的轴力,M为测试管道的弯矩,hA、hC分别为点A、C距离中性轴的距离,σA、σC分别为点A、C处的应力,R为管道的外半径,r为管道的内半径,S为管道的横截面积.

取管道与地表的摩擦系数为0.3,管道在孔内的摩擦系数为0.25,泥浆密度为1.2 t/m3,钢管的弹性模量为2.05×105MPa.将实际的三维管道穿越路线进行平面拟合,并将其投影至平面,对投影点进行最小二乘法线段拟合,如图6所示.同时得出关键点的拐角,如表1所示.1、7分别为管道路线入口和管道路线与水平面的交点,2～6分别为拟合后的管线拐点,x为水平方向坐标值,y为竖直方向坐标值.

将上述关于管道路线、土体和管材等条件分别代入GB 50424-2007、PRCI方法以及本文方法的回拖力计算公式中,得到的结果如图7所示.图中,T为回拖力,i为管线的各个关键点,i=1,2,3,4,5,6,7.在管道回拖力的计算上,PRCI方法和GB 50424-2007在计算结果上相差无几；本文方法的计算结果与PRCI方法和GB 50424-2007在整体趋势上保持一致,数值上存在一个较稳定的差值.实测值是保证管道顺利安全穿越,钻机所保持的回拖力,理论上应为设计值的最大值乘以安全系数,该工况的实测值远大于计算最大值,偏于保守.

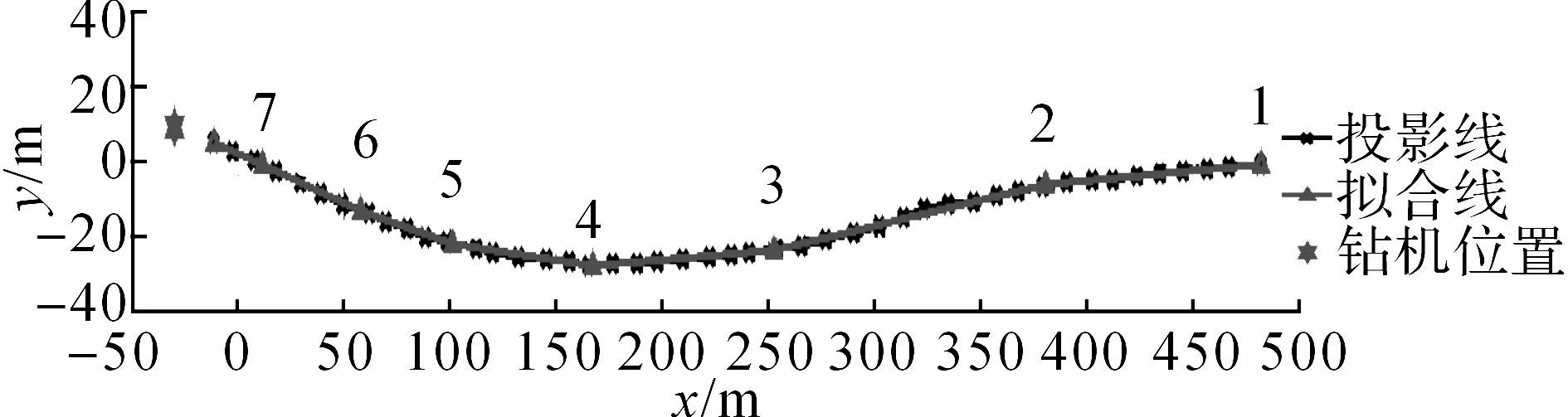
图6 管道路线拟合图Fig.6 Fitting diagram of pipe route

关键点α/(°)23．4136．8948．1654．8464．80

图7 各种回拖力计算公式的结果对比Fig.7 Contrast of calculation results of different pullback force formulas

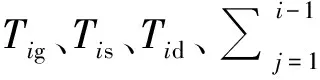
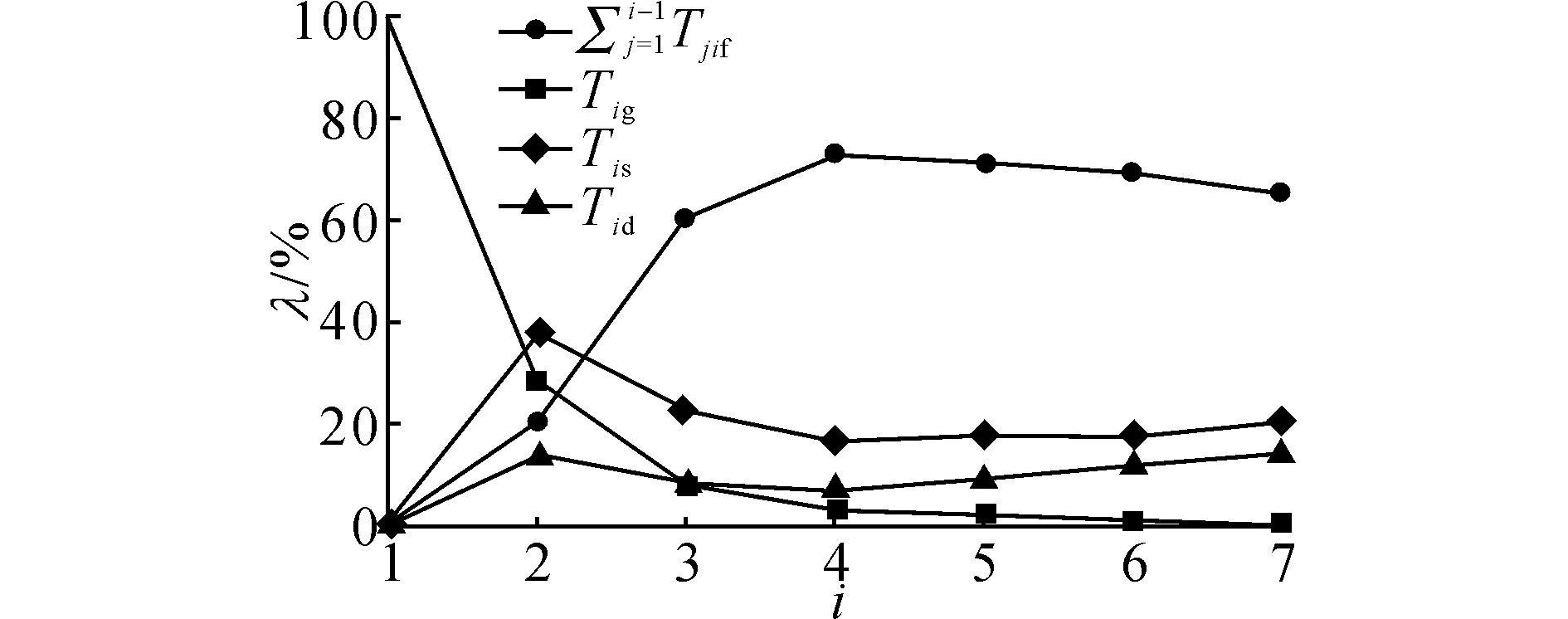
图8 回拖力各组成部分的比例Fig.8 Proportion of each component of pullback force

图9 回拖力与拐角的关系曲线Fig.9 Relation of pullback force and transit angle

改变拐角最大的4点处拐角α,研究管道回拖至点7处时T的变化情况.如图9所示,回拖力随着拐角的变化呈指数增加.以该穿越工程为例,选用的钻机可提供的最大拉力为1 200 kN,理论上以回拖力为限制条件,拐角不应超过20.6°.同理,该方法可以为相似穿越工程的路线设计和HDD钻机的工作机制设计提供依据.

5 结 论

(1) 本文提出的回拖力计算公式充分反映了管道在回拖各个阶段的受力情况,比GB 50424-2007、PRCI的方法接近实际情况,且与GB 50424-2007、PRCI计算结果的稳定差值反映出所考虑的泥浆阻力和管道弯曲大变形阻力.

(2) 纵观管道的整个回拖过程可知,在回拖前期阶段,影响最大的是管道与地表面的摩擦力；在后期阶段中,影响最大的是管道弯曲大变形阻力；泥浆阻力和管道与孔壁的摩擦力相对影响较小.在整个回拖过程中,可以通过调整管道拐角来有效减小施工所需要的回拖力.

(3) 回拖力随管线大转角处拐角的增加呈指数增长.在实际施工中,可以预先根据采用的钻机型号,利用拐角与回拖力的关系图来判断穿越路线中的拐角是否合理,从而使得整个施工过程能够安全进行.

[1] 王军,吴君侯,章宇,等.上海地区深基坑工程的环境安全问题[J].岩土工程学报, 2007, 28(B11):1328-1331. WANG Jun, WU Jun-hou, ZHANG Yu, et al. Environmental safety of deep excavation engineering in Shanghai [J]. Chinese Journal of Geotechnical Engineering, 2007, 28(B11): 1328-1331.

[2] 颜纯文. 2013年非开挖行业统计分析[C]∥2014年非开挖技术会议论文集. 广东：[s.n.], 2014: 1-11. YAN. Chun-wen. Review and analysis of trenchless technology in 2013 [C]∥International Trenchless Technology Conference. Guangdong: [s.n.], 2014: 1-11.

[3] 马保松.非开挖工程学[M].北京:人民交通出版社, 2008: 532.

[4] 颜纯文, STEIN D. 非开挖地下管线施工技术及其应用[M].北京:震出版社, 1992: 74.

[5] 安金龙.水平定向钻穿越回拖力的计算方法及其分析[J].石油工程建设, 2008, 34(1):21-26. AN Jin-long. Calculation and analysis of pull-back force of pipeline crossing by horizontal directional drilling [J]. Petroleum Engineering Construction, 2008, 34(1):21-26.

[6] 刘大鹏,尤晓伟.土力学[M].北京:清华大学出版社,北京交通大学出版社,2005: 58.

[7] GB 50424-2007,油气输送管道穿越工程施工规范[S].北京：中国计划出版社,2008:17.

[8] GB 50268-2008,给水排水管道工程施工及验收规范[S].北京：中国建筑工业出版社,2008: 99.

[9] ASTM F1962-99, Standard guide for use of maxi-horizontal directional drilling for placement of polyethylene pipe or conduit under obstacles, including rivers crossings[S]. West Conshohocken: ASTM International, 2005.

[10] HUEY D P, HAIR J D, MCLEOD K B. Installation loading and stress analysis involved with pipelines installed by horizontal directional drilling [R]. Chicago： North American Society for Trenchless Technology,1996.

[11] BAUMERT M E, ALLOUCHE E N. Methods for estimating pipe pullback loads for horizontal directional drilling (HDD) crossings [J]. Journal of Infrastructure Systems, 2002, 8(1): 12-19.

[12] POLAK M A, LASHEEN A. Mechanical modelling for pipes in horizontal directional drilling [J]. Tunneling and Underground Space Technology, 2001,16(supple.1): 47-55.

[13] POLAK M A, CHU D. Pulling loads for polyethylene pipes in horizontal directional drilling: theoretical modeling and parametric study [J]. Journal of Infrastructure Systems, 2005, 11(2): 142-150.

[14] CHENG E, POLAK M A. Theoretical model for calculating pulling loads for pipes in horizontal drectional drilling [J]. Tunneling and Underground Space Technology, 2007, 22(5): 633-643.

[15] 蔡亮学,何利民,吕宇玲,等.水平定向钻管道穿越孔底泥浆的力学特性[J]. 油气储运, 2011, 30(1): 25-29. CAI Liang-xue, HE Li-min, LV Yu-ling, et al. Hole-bosom slurry mechanical properties of horizontal directional drilling in pipeline crossing project [J]. Oil and Gas Storage and Transportation, 2011, 30(1): 25-29.

[16] 李翔,李素贞.管道穿越大角度借转附加应力分析[R].上海：同济大学,2015. LI Xiang, LI Su-zhen. The additional stress analysis of pipeline in the big angle corner [R]. Shanghai: Tongji University, 2015.

[17] LI S. Construction monitoring of a municipal gas pipeline during horizontal directional drilling [J]. Journal of Pipeline Systems Engineering and Practice, 2013,4(4): 04013005.

Analysis and measurement on pullback force of steel pipeline during horizontal directional crossing

LI Su-zhen1,2, LI Xiang1

(1.DepartmentofBuildingEngineering,TongjiUniversity,Shanghai200092,China；2.StateKeyLaboratoryofDisasterResearchinCivilEngineering,TongjiUniversity,Shanghai200092,China)

The determination of pullback force on the pipeline during installation is critical to the successful implement of pipeline crossing. The domestic and international standards regarding the calculation of pullback force were summarized and compared. The main difference among these regulations lies in the analysis of the resistances due to mud flow and pipeline large deformation. The new method was proposed based on the evaluation on the accuracy of the two resistance models in order to calculate the pullback force of a steel pipeline during horizontal directional drilling (HDD) construction. The analysis on the mechanical behavior of pipeline was conducted. A practical engineering project on the installation of a gas pipeline was employed. The proposed method accorded with the actual situation. The resistance caused by pipeline large deformation is a dominant factor contributed to the total pullback force. The pullback force increased exponentially with the increase of the transit angle due to pipeline deformation.

horizontal directional crossing; pullback force; mud flow resistance; pipeline large deformation; construction monitoring

2015-10-20. 浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

土木工程防灾国家重点实验室自主研究课题基金资助项目(SLDRCE14-B-19);霍英东教育基金会高等院校青年教师基金资助项目(142004).

李素贞(1978—),女,副教授，从事生命线工程的研究.E-mail: lszh@tongji.edu.cn

10.3785/j.issn.1008-973X.2016.04.016

TU 990

A

1008-973X(2016)04-0714-06