考虑随机故障的流水线调度问题前摄优化方法
2016-12-22赵婵媛陆志强崔维伟
赵婵媛, 陆志强, 崔维伟
(1.同济大学 机械与能源工程学院, 上海 201804; 2.上海交通大学 工业工程与管理系, 上海 200240)
考虑随机故障的流水线调度问题前摄优化方法
赵婵媛1, 陆志强1, 崔维伟2
(1.同济大学 机械与能源工程学院, 上海 201804; 2.上海交通大学 工业工程与管理系, 上海 200240)
研究带有随机故障的流水线车间调度问题, 以质量鲁棒性和解鲁棒性的综合指标为优化目标, 分析故障这一随机因素的影响, 采用前摄优化理论求解问题. 建立问题的随机规划数学模型,设计内、外两层嵌套式优化算法以联合决策工件调度顺序与缓冲时间大小. 在外层, 以NEH启发式算法为基础,结合邻域搜索决策工件加工顺序;在内层, 采用遗传算法搜索缓冲时间并设计有效的代理指标作为解的评价方式. 数据实验表明, 提出的算法相比2种传统方法所得到的解的综合指标更优异, 且允许决策者根据不同的偏好选择不同的优化解. 加入缓冲时间有利于改善解鲁棒性指标,可以提高质量鲁棒性的稳定度.
流水线; 随机故障; 鲁棒性; 代理指标
传统流水线调度问题多假设机器在调度期内随时可用, 而在实际生产中受不确定性因素的影响,机器可能发生意外故障,会导致调度的执行偏离计划预期,影响生产交付及物料调配.解决不确定性调度问题的方法主要有3种:前摄调度、反应调度以及前摄-反应调度.
前摄调度是指在生成基础调度时考虑不确定因素的影响,通常以鲁棒性为优化目标,以期减少不确定性对调度产生的干扰,适用于随机事件的可预知性较好且每次随机事件本身单独对调度解的影响较小的情况.计算机仿真技术与优化算法的有效结合是解决前摄调度优化问题的一种重要方法.Zandieh等[1-3]结合仿真与元启发式算法,求解具有随机性的混合流水线或作业车间的调度问题.冗余调度是前摄调度中提高解鲁棒性的常用手段,它利用多余的资源应对不确定性情况的发生[4].Mehta等[5-6]通过插入缓冲时间来吸收故障干扰,试图改善单机调度中的解鲁棒性,采用的缓冲时间均为故障间隔期望值.
反应调度指在调度初期不考虑不确定因素,而在突发事件发生后根据特定的规则进行调度,适用于随机性大或随机性小但单次随机事件对整个调度影响较大并且无法事先预知的情况.反应调度的优点是能够在短时间内得到可接受的解,但通常不能达到全局最优[7].分派规则可以被看作是反应调度的一类典型规则,专家学者针对混合流水线或作业车间提出若干不同的分派规则,对不可预知的不确定性情况作出响应[8-12].
前摄-反应调度结合前两者,适用于已知部分不确定性,但可能遇到突发事件的情况,严重偏离基础调度时运用重调度进行修正.Katragjini等[13]考虑流水线调度的3种不确定性,运用仿真结合启发式算法求解基础调度,比较4种重调度策略.Wang等[14]提出聚类分组法求解混合流水线调度问题,工件根据不确定性的大小分组,不确定性大的运用分派规则即反应调度,不确定性小的运用前摄-反应调度.Rahmani等[15]针对考虑随机加工时间及新工件到达的两机流水线提出前摄-反应调度方法,前摄调度考虑随机加工时间,而新工件到达则触发反应调度.
本文针对考虑随机故障的流水线问题,已知机器失效函数服从指数分布,属于可预知性较好的情况.运用前摄调度策略,在调度时考虑故障的影响,以质量鲁棒性和解鲁棒性的综合指标为优化目标,旨在求得受故障干扰影响小、并且能够维持绩效较好的解.当数据规模大时,采用仿真优化方法难以在短时间内求得数值解,本文提出有效代理指标代替抽样仿真模块的功能,可以大幅度地节省算法迭代搜索的时间.
1 问题描述与数学模型
1.1 问题描述
以流水线车间为研究对象,即m台机器构成的纯流水线系统,各机器之间的存储容量无限.在调度计划周期内共有n个不同类型的工件,每个工件均需依次经过每台机器,且在每台机器上只加工一次,工件的每道工序在机器上的加工时间已知,工件i在机器k上的加工时间为pik,所有工件在零时刻同时到达系统.任何机器在加工工件时都可能发生意外故障,故障的发生服从指数分布,即故障率为常量,记为λk.故障后须对机器进行小修,小修时间为tk,修复结束后被打断的工件继续加工,即工件属于可恢复(resumable)情形.
机器一旦发生故障后需要进行维修,会对基础调度产生影响,因此需要一定的重调度策略来修正基础调度.采用的重调度策略为右移规则,即工件作业顺序维持不变,未完成的加工延至维修后,并规定工件的实际完成时间不得早于预测,即若工件比预测完成时间提前,则该工件不被运送到下一台机器上,该机器也不继续加工下一个工件,以协调实际生产调度中外部资源如原材料、工具及搬运设施等的调度.
在已有文献中,确定性流水线调度的绩效评估通常采用制造期(makespan)等目标值,然而考虑故障等不确定性因素时常采用鲁棒性指标(robustness).鲁棒性指标可以分为质量鲁棒性和解鲁棒性两种.质量鲁棒性是指调度计划的绩效不会因为随机干扰的影响而大幅降低,解鲁棒性是指实际调度的具体执行情况和初始调度计划没有太大的偏差[1].基础调度计划是安排原材料供给、换模、报价及交付等的重要依据,一旦更改会产生库存、运输、延期罚款等成本,并使得预定的计划不可行,因此解鲁棒性变得越来越重要.
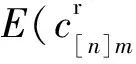
1.2 数学建模
定义的决策变量如下.
xi[j]:0/1变量, 表示工件i在第j个位置进行加工,i=1,2,…,n,j=1,2,…,n.
I[j]k:排在第j个位置的工件 (以下简记为工件[j]) 在机器k上加工后的缓冲时间.
辅助变量如下.
p[j]k:工件[j]在机器k上的加工时间,j=1,2,…,n,k=1,2,…,m.
s[j]k:基础调度中工件[j]在机器k上开始加工时间.
c[j]k:基础调度中工件[j]在机器k上完成加工时间.
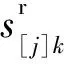
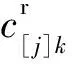
N[j]k:工件[j]在机器k上加工时发生故障的次数.
根据问题描述及假设, 建立数学模型如下.
(1)
s.t.

(2)

(3)

(4)
s[1]1=0,
(5)
c[j]k=s[j]k+p[j]k+I[j]k,∀j,∀k,
(6)
s[1]k=c[1],k-1,k≥2,
(7)
s[j]1=c[j-1],1,j≥2,
(8)
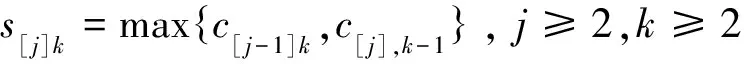
(9)
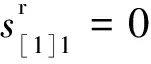
(10)

(11)

(12)
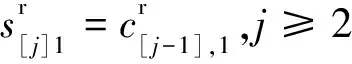
(13)

(14)
xi[j]=0 或 1.
(15)
目标函数为质量鲁棒性与解鲁棒性的线性组合,如式(1)所示.式(2)、(3)表示每个工件能且只能被安排到加工顺序中的一个位置,同时加工顺序中的每个位置能且只能安排一个工件.式(4)表示工件的加工时间与决策变量之间的对应关系.式(5)~(9)表示前摄调度中工件开始加工时间和完成加工时间的递推式,其中式(6)表示在前摄调度中加入缓冲时间,相当于人为延长加工时间,以吸收机器故障对调度产生的影响.式(10)~(14)表示实际调度中一旦发生故障,运用右移策略进行重调度.式(11)中,N[j]k体现了机器发生故障的随机性,使得模型无法作为确定性问题求解.
2 算法设计
2.1 内、外层循环算法设计
由上述数学模型可以看出,决策变量为0/1整数变量xi[j]和实数变量I[j]k, 其余变量均为辅助间接变量, 这使得该混合整数规划数学模型难以直接求解.由于缓冲时间的最优取值非常依赖于工件的加工顺序,采用内、外两层嵌套式优化算法解决上述调度问题:外层决策工件顺序,内层决策缓冲时间.该外模型具有随机性,传统方法通常以数理统计原理,运用仿真方法求出目标函数的统计值,为了让统计值具有意义,需要运行一定的重复次数,因而耗时久不利于大规模数据的内、外层搜索,如m=10、n=50、仿真重复次数为1 000次时无法在几天内求得解,因此本文提出代理指标,以确定性解析函数式代替目标函数,节省内、外层搜索时间.算法框架如图1所示.外层算法Procedure1以NEH启发式算法为基础,结合邻域搜索决策工件加工顺序;内层算法Procedure2针对给定的工件顺序,设计基于有效代理指标的遗传算法,对缓冲时间进行有效搜索求解.
2.1.1 外层算法Procedure1: 决策工件顺序
3) 取排在第3个的工件, 分别插入到已有排序的各个空挡中, 即σ1(j[3],j[1],j[2])、σ2(j[1],j[3],j[2])和σ3(j[1],j[2],j[3]), 比较各排序在插入缓冲时间后的目标值s1、s2和s3, 保留最优的排序.
4) 根据步骤2)、3)类推, 直到n个工件全都进行了比较, 此时最优值为sbest, 最优解为σbest.
5) 记重复迭代次数r=0, 最大重复迭代次数为rmax.

图1 双层嵌套式算法框架Fig.1 Famework of two-loop nested algorithm
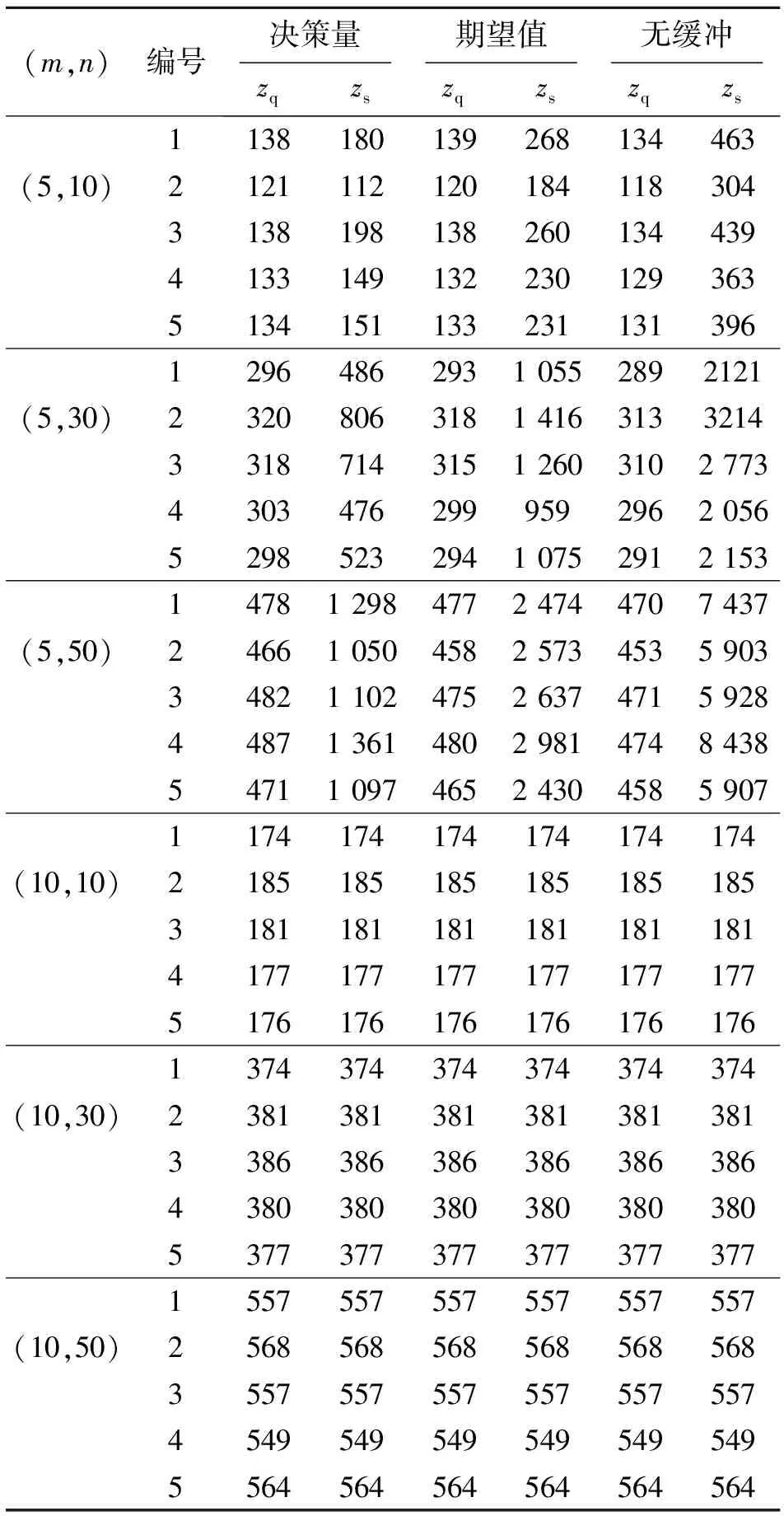
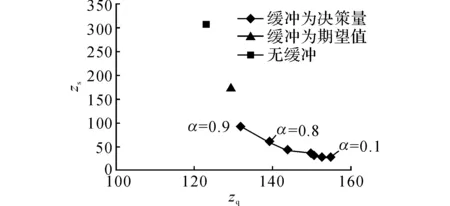
6) 随机取出排在第w(w 7) 若st 8) 若r 2.1.2 内层算法Procedure2: 计算缓冲时间 初始种群:种群数量是影响算法最优化性能和效率的因素之一,目前常用的种群数目为20~200,本文取种群数量为200.初始种群中1条初始染色体中各基因均为0,其余199条染色体为随机生成. 选择机制:轮盘赌法;跨世代精英策略,即选择最优的种群数量个染色体直接进入下一代. 交叉机制:采用中间重组的方法,适用于实变量,子个体的产生由式(16)产生.若子个体<0,则子个体=0,其中ρ随机取[0.75,1.25]的实数,通过数值试验调试,取交叉概率Pc=0.85.子个体=父个体1+ρ×(父个体2-父个体1). (16) 变异机制:随机选择变异位置,重新随机生产该位置的基因,通过数值试验调试,取变异概率Pm=0.25. 终止条件:为了控制两层嵌套算法的运行时间,限制最大的迭代步数tmax,通过数值试验调试,取tmax=100. 解的评价(适应度函数设计):对于一个给定的解(包括工件顺序与染色体编码对应的缓冲时间),由于机器故障概率以及反应调度规则的影响,无法直接推导出解的目标函数值,即质量鲁棒性与解鲁棒性对应的数学期望表达式,而仿真抽样需要重复计算一定次数,耗时较长,因此设计如2.2节所述的代理指标作为适应度函数,以表达式的形式求得目标函数的近似值. 2.2 代理指标 由于数学模型中的N[j]k是一个随机量, 导致目标函数zq与zs具有随机性, 通常由仿真来得到数值解.仿真的方法耗时较久,尤其对于大规模问题,难以在短时间内计算得到解.本文设计相应的代理指标作为目标函数的近似函数,本质上是以基于代理指标的确定性优化问题代替随机优化模型,达到极大地减少算法运行时间的目的. 2.2.1 代理指标的相关分析 目标函数中的质量鲁棒性zq用c[n]m来替代, 与文献[5,6]的研究一致. 解鲁棒性zs体现的是基础调度与实际的偏离程度, 突发故障、流水线调度系统固有的空闲时间以及人为插入的缓冲时间都会对zs造成影响, 因此提出的代理指标综合考虑了这三者之间的关系,突发故障体现在实际调度中,而后两者体现在基础调度中.提出的替代指标主要考虑机器故障发生后是否会对后续工件的完成加工时间产生影响,如果后续总的空闲时间不为0,则能够在一定程度上改善实际生产与基础调度的偏离程度,从而改善zs;若后续空闲时间不小于故障小修时间,则说明空闲时间能够完全吸收故障的影响,计划与实际没有偏离.以故障时间与可用时间之差的加权和来体现空闲时间是否吸收了故障干扰,即体现基础调度与实际的偏离程度zs. 图2 带有缓冲时间的流水线基础调度甘特图Fig.2 Gantt chart of flow shop baseline schedule with buffer time (17) P[j]k=1-exp (-λk·p[j]k),∀j,∀k, (18) (19) (20) (21) (22) ∀j,∀k,a>j,b>k, (23) ∀j,∀k,a≥j,b≥k. (24) 2.2.2 代理指标的验证 运用VS C#进行编程, 通过仿真数据实验对前述代理指标进行评价, 比较原目标函数与代理指标的相关性及计算用时. 本文采用置信区间法计算仿真重复次数, 取显著水平为1%, 求得重复次数为1 000. 如表2所示为每组不同的缓冲时间下计算代理指标与仿真值的平均用时,按算例进行统计,记TSM为计算代理指标的平均时间,TSP为计算仿真值的平均用时.可以看出,当m=10,n=50时, 采用仿真的方法需要近0.08 s来计算一次目标值, 约为同等参数下代理指标所用时间的10倍;对于内层求解缓冲时间的遗传算法,仅用于计算适应度函数的仿真时间将达1 600 s;嵌套进外层算法经过千次的迭代会使算法难以在几天内求得解, 运用代理指标能够有效地减少计算时间. 3.1 本文算法与传统方法的比较 实验参数如2.2.2节所述, 不同数据规模下各生成5组包含不同机器故障率和维修时间的算例.比较本文算法(取α=0.9,β=0.1)与传统方法的目标值zq和zs.传统方法分别为:缓冲时间为故障维修时间期望(单机调度中通常令缓冲时间等于期望值[4],即I[j]k=λk·p[j]k·tk)以及无缓冲时间(即α=1,β=0).从表3可以看出,无缓冲的方法相比其余方法虽然得到的zq最好, 但zs最差, 体现所得解在故障环境下不稳定的特征. 本文算法虽然牺牲了一小部分zq, 但所得的zs远比缓冲为期望值的算法更好, 且数据规模越大,本文算法的优越性越显著. 表1 代理指标与仿真值的相关度系数 表3 不同算例下求解缓冲时间方法的比较 3.2 质量鲁棒性与解鲁棒性的权衡 质量鲁棒性和解鲁棒性之间需要权衡,以二者带权重的线性组合为目标函数来解决多目标问题, 不同权重下得到不同偏好的解.以n=10、m=5的情况为例,比较不同权重下的zq和zs,图3展示了缓冲为决策量、缓冲为期望值以及无缓冲所得到的解.无缓冲(α=1,β=0)时所得到解的zq最好,而加了缓冲时间能够明显改善zs,当α=0.9,β=0.1时的zq已接近缓冲为期望值时的解,而zs优于后者,因此可以使用本文方法牺牲一小部分质量鲁棒性以获取解鲁棒性的显著改善.在生产过程中,可以根据实际情况灵活选取权重α和β. 图3 不同决策方法下质量鲁棒性与解鲁棒性的对比图Fig.3 quality robustness and solution robustness under different decision methods 图4 不同方法的质量鲁棒性分布概率Fig.4 Probability distribution of quality robustness under different methods 如图4所示为上述例子中不同权重下缓冲时间为决策量时与缓冲均为期望值时zq的分布概率Pd比较. 从图4(a)~(c)可以看出,zq的权重越大,均值越小但更分散,而缓冲时间为决策量比为期望值时的zq分布更集中.如图4(d)所示为无缓冲与缓冲为期望值时zq的分布比较.可以看出,无缓冲时zq的概率分布最分散.即使不考虑zs而只考虑zq的稳定性,也有必要插入一定的缓冲时间. 如图5所示为不同方法的甘特图比较.图中,t为时间,N为机器序号.可以看出,当不考虑缓冲时间(α=1,β=0)时,由于流水线上、下游之间的关系,系统存在少量的空闲时间,但这些空闲时间不足以吸收故障带来的对调度的干扰.缓冲为决策量(α=0.9,β=0.1)与缓冲为期望值相比,所得的缓冲时间不同.缓冲为期望值时均匀地在调度中加入了少量缓冲时间;当缓冲为决策量时,在较易发生故障的机器和相应较易发生故障的时间上加入缓冲时间,并且受调度的影响,在加工任务紧时自动减少缓冲时间.由前述结论已知,两者的质量鲁棒性zq相接近,而缓冲为决策量时的解鲁棒性zs较优,由此可见使用本文算法能够更好地改善解鲁棒性. 本文设计了内、外两层嵌套式的前摄优化调度算法,以求解带有随机故障的流水线调度问题.以质量鲁棒性和解鲁棒性综合指标作为目标函数,结合流水线的特点提出代理指标,并证明了代理指标的有效性.与仿真方法相比,可以大幅地节省计算时间.不同数据规模下的实验结果显示,本文算法与2种传统方法相比,所得到的解的综合指标更优异;此外,通过算例说明了双目标不同权重下目标值的变化情况,决策者可以根据偏好选择相应解.未来的工作方向是在本文研究的流水线环境下前摄调度基础上, 考虑多种不确定性, 依据机器状态、故障概率研究由不同反应规则构成的反应调度,设计相应的前摄-反应调度算法. [1] ZANDIEH M, GHOLAMI M. An immune algorithm for scheduling a hybrid flow shop with sequence-dependent setup times and machines with random breakdowns [J]. International Journal of ProductionResearch, 2009, 47(24): 6999-7027. [2] CHAARI T, CHAABANE S, LOUKIL T, et al. Agenetic algorithm for robust hybrid flow shop scheduling [J]. International Journal of Computer Integrated Manufacturing, 2011, 24(9): 821-833. [3] 陈勇,潘益菁,王亚良,等.多态性作业车间鲁棒调度CA-GA建模[J].浙江工业大学学报, 2014(2): 124-131. CHEN Yong, PAN Yi-jing, WANG Ya-liang , et al. Research on modeling of robust scheduling for polymorphism job shop based on cellular automata and genetic algorithm [J]. Journal of Zhejiang University of Technology, 2014(2): 124-131. [4] HERROELEN W, LEUS R. Project scheduling under uncertainty: survey and research potentials [J]. European Journal of Operational Research, 2005, 165(2):289-306. [5] MEHTA S V, UZSOY R. Predictable scheduling of a single machine subject to breakdowns [J]. International Journal of Computer Integrated Manufacturing, 1999,12(1): 15-38. [6] LIU L, GU H, XI Y. Robust and stable scheduling of a single machine with random machine breakdowns [J]. International Journal of Advanced Manufacturing Technology, 2007, 31(7/8): 645-654. [7] RAJENDRAN C, HOLTHAUS O. A comparative study of dispatching rules in dynamic flowshops and jobshops [J]. European Journal of OperationalResearch, 1999, 116(1): 156-170. [8] KIANFAR K, GHOMI S M T F, KARIMI B. New dispatching rules to minimize rejection and tardiness costs in a dynamic flexible flow shop [J]. International Journal of Advanced Manufacturing Technology, 2009, 45(7/8): 759-771. 图5 不同方法下的基础调度甘特图比较Fig.5 Comparison of Gantt charts under different baseline schedules with different methods [9] HASAN S M K, SARKER R, ESSAM D. Genetic algorithm for job-shop scheduling with machine unavailability and breakdowns [J]. International Journal of Production Research, 2011, 49(16): 4999-5015. [10] 丁帅,李铁克,施灿涛. 考虑机器故障的HFS重调度研究[J]. 计算机工程与应用, 2012, 48(23): 234-238. DING Shuai, LI Tie-ke, SHI Can-tao. Study of hybrid flow shop rescheduling with consideration of machine breakdown [J]. Computer Engineering and Applications, 2012, 48(23): 234-238. [11] BAI D. Asymptotic analysis of online algorithms and improved scheme for the flow shop scheduling problem with release dates [J]. International Journal of Systems Science, 2015, 46(11): 1994-2005. [12] ZHAO F, LI N. Flow time and tardiness based on new scheduling rules for dynamic shop scheduling withmachine breakdown [J]. Mechatronics Engineering, Computing and Information Technology, 2014, 556-562: 4412-4416. [13] KATRAGJINI K, VALLADA E, RUIZ R. Flow shop rescheduling under different types of disruption [J]. International Journal of Production Research, 2013, 51(3): 780-797. [14] WANG K, CHOI S H, QIN H, et al. A cluster-based scheduling model using SPT and SA for dynamic hybrid flow shop problems [J]. International Journal ofAdvanced Manufacturing Technology, 2013, 67(9-12): 2243-2258. [15] RAHMANI D, HEYDARI M. Robust and stable flow shop scheduling with unexpected arrivals of new jobs and uncertain processing times [J]. Journal of Manufacturing Systems, 2014, 33(1): 84-92. Proactive scheduling optimization on flow shops with random machine breakdowns ZHAO Chan-yuan1, LU Zhi-qiang1, CUI Wei-wei2 (1.DepartmentofMechanicalandEnergyEngineering,TongjiUniversity,Shanghai201804,China;2.DepartmentofIndustrialEngineeringandLogisticsManagement,ShanghaiJiaotongUniversity,Shanghai200240,China) Flow shop scheduling problems with random machine breakdowns were analyzed in order to optimize the bi-objective of quality robustness and solution robustness. The impact of breakdowns was analyzed by proactive scheduling theory. A stochastic programming mathematical model was proposed. Then the nested algorithm with two loops was developed to simultaneously determine jobs’ sequence and buffer time. The outer optimization loop combined NEH algorithm and neighborhood search method to determine jobs’ sequence. The inner loop adopted the genetic algorithm to optimize the buffer time with an effective surrogate measure, which was adopted as the evaluation method of solutions. Computational results indicate that the solution performance can be significantly improved with the proposed algorithm comparing with the traditional ways, and decision makers can choose different biased solutions according to their preference. Inserting buffer time improved the solution robustness and increased the stability of quality robustness. flow shop; random machine breakdown; robustness; surrogate measure 2015-04-03. 浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng 国家自然科学基金资助项目(71171130, 61273035). 赵婵媛(1990—), 女, 硕士生, 从事串行生产线生产调度的研究. ORCID: 0000-0002-6582-2860. E-mail: zhchy90@hotmail.com 通信联系人: 陆志强, 男, 教授. ORCID: 0000-0002-9357-610X. E-mail: zhiqianglu@tongji.edu.cn 10.3785/j.issn.1008-973X.2016.04.007 F 224 A 1008-973X(2016)04-0641-09

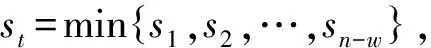










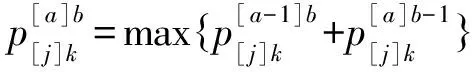

3 数据实验


4 结 语

