基于动态PLS框架的多变量无静差预测控制
2016-12-22金鑫,梁军
金 鑫, 梁 军
(浙江大学 控制科学与工程学院,浙江 杭州 310027)
基于动态PLS框架的多变量无静差预测控制
金 鑫, 梁 军
(浙江大学 控制科学与工程学院,浙江 杭州 310027)
针对动态偏最小二乘(DyPLS)建模方法容易导致模型与实际系统的失配,使控制系统产生静差的问题,提出基于DyPLS框架的多变量系统无静差模型预测控制(MPC)方法.将基于状态空间模型的MPC方法推广到DyPLS框架下.在内模型中采用状态空间模型描述系统的动态过程,利用该模型设计MPC控制器.该方法将内模型的状态作为控制系统的反馈,由于模型的失配导致该状态不能准确地描述系统的实际状态,导致了静差的存在.对该框架下的状态空间模型进行增广,引入扰动模型,利用状态观测器估计系统输出与模型输出的偏差.给出该增广模型的能观测性条件.为了采用卡尔曼滤波器的方法求取观测器的增益矩阵,分析原空间的数据投影到潜变量空间后变量方差的变化情况.该方法在控制中引入了输出反馈,保证了控制的无静差跟踪特性,能够抑制系统中的不可测扰动.Jerome-Ray的精馏塔模型的仿真结果验证了该方法的有效性.
偏最小二乘;模型预测控制(MPC);状态空间模型;无静差控制
模型预测控制(MPC)是一种利用数学模型来预测系统输出的启发式控制方法. MPC算法使用的模型有阶跃、脉冲响应模型或输入输出模型. Muske等[1]提出基于状态空间模型的预测控制算法.输入输出模型可以转换成状态空间模型[2].基于状态空间模型的MPC算法得到了广泛的应用.
保证系统输出对设定值的无静差跟踪是控制系统的重要性能指标之一.在过程存在扰动或者模型和过程不匹配时,这一指标显得更重要.解决该类无静差控制问题主要有以下3种方法.1)利用扰动模型对系统的状态模型进行增广.增广后的系统可以处理扰动和模型失配的问题[3-5].2)利用内模原理的思想,将积分器一类的设定值的内模型纳入到控制器中[6-8].3)将状态空间模型改写成增量的形式[9-10].增量状态空间模型的状态变量由原模型的状态变量的增量和原模型输出的增量组成,而模型的输入变量是系统的控制增量.
计算机技术的发展使得利用海量大维数的数据建模成为可能.对于大维数的数据来说,不同变量间的数据具有较高的相关性.而系统的运行范围往往小于数据所代表的维数,因此,发展出提取主元的数据降维方法.偏最小二乘(partial least square, PLS)是用于建立两组数据间函数关系的降维建模方法.PLS算法的优点是能够将多变量的回归问题解耦成多个不相关的单变量回归问题,并能够处理非方系统和数据的病态问题.利用PLS降维和自动解耦的特点,许多学者将其应用于动态过程数据的建模.Kaspar等[11-12]将PLS的负载矩阵P和Q作为实际系统的预补偿器和后补偿器,通过这两种补偿器来描述系统的动态过程.Chen等[13]在PLS的内模型中引入ARX模型来描述动态过程.Laur 等[14]提出基于PLS的MPC相关辨识方法来得到DyPLS模型. 随着这些动态PLS建模方法的发展,许多新的控制策略得以提出.Kaspar等[11]提出DyPLS框架下的PID控制策略.Chen等[13]在此基础上提出具有解耦结构的多回路自适应PID控制策略.Hu等[15-16]将内模控制策略拓展到DyPLS模型中,得到了较好的抑制扰动的性能.Lv等[17]提出多回路的约束控制策略,研究DyPLS框架下MPC变量约束的处理方法.
本文将状态空间模型MPC方法拓展到DyPLS框架下,对DyPLS潜变量空间中的每个子模型分别设计独立的状态空间模型MPC控制器.通过引入扰动模型和状态观测器的方法来保证控制器的无静差跟踪性能.
1 DyPLS 建模和控制方法
1.1 DyPLS 建模方法
传统的PLS算法由提取主元的外模型和建立输入输出数据得分矩阵函数关系的内模型组成[18].假定X和Y分别表示一个l×m维的输入数据矩阵和一个l×n维的输出数据矩阵, 其中l、m和n分别为样本个数、输入变量的维数和输出变量的维数.
通过对X和Y进行迭代计算提取主元来获得PLS的外部模型:
(1)
式中:R为主元(潜变量)个数 (由于PLS的降维特性,通常情况下R满足R≤max(m,n));pr和qr分别为负载矩阵P和Q的第r个负载向量;tr和ur分别为得分矩阵T和U的第r个得分向量;E*和F*分别为X和Y的残差矩阵.
在内模型中,通过对T和U进行最小二乘计算,可以得到回归矩阵B.
(2)
式中:
B=(TTT)-1TTU=diag [b1,…,bR] ;
T=[t1,t2,…,tR]T.
将式(2)代入式(1),可以得到输入输出数据矩阵的回归方程:
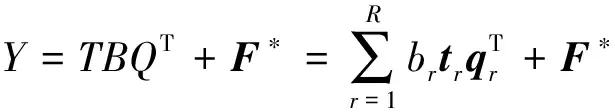
(3)
传统PLS方法的回归方程仅具有代数方程的结构,因而无法处理动态系统的建模问题.许多学者通过引入时间序列分析或者动态滤波器的方法来改进传统的PLS结构,使其能够处理动态系统的建模问题.本文采用Lakshminaravanan 等[19]提出的以ARX模型作为PLS的内模型来描述得分矩阵间动态关系的方法来描述系统的动态特性.内模型的结构为
ur(k)=Ar(q-1)ur(k-1)+Br(q-1)tr(k)+ξr(k)=[ur(k-1),…,ur(k-na),tr(k-1),…,tr(k-nb)]×
[ar,1,…,ar,na,br,1,…,br,nb]T+ξr(k)=

(4)
式中:
Ar(q-1)=-ar,1-ar,2q-1-ar,naq-na+1,
Br(q-1)=br,1q-1+br,2q-2…+br,nbq-nb,
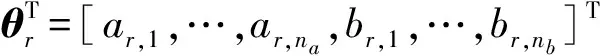
U(k)QT+F*(k) .
(5)
式中:U(k)=diag[u1(k),u2(k),…,uR(k)].
1.2 DyPLS 框架下的控制器设计
Kaspar等[12]提出的DyPLS控制器设计框架如图1所示.图中,Wx和Wy为输入数据X和输出数据Y对角形式的权重矩阵,作用是对数据进行归一化处理;Gc、Gp和Gd分别表示控制器、被控对象和系统的扰动;P和Q分别为输入数据X和输出数据Y的负载矩阵;Q+为Q的逆矩阵;Yset为系统的设定值;D为系统的扰动序列.与传统控制策略将实际物理量作为控制器的输入和输出响应不同的是,该框架将系统的输入和输出投影到潜变量空间中,控制器的输入是得分矩阵U,输出是得分矩阵T,潜变量空间中的各个子控制器同时对Yset在潜变量空间中的投影Uset和U的偏差进行响应.将求出的控制器输出T反投影到原空间中,作为系统的输入信号发送给系统的执行器.该DyPLS框架的优点是将多输入多输出(multiple input multiple output, MIMO)系统解耦成潜变量空间中的多个单输入单输出(single input single output, SISO)子系统,使多变量系统的控制问题转化为相互独立的多个SISO控制问题.
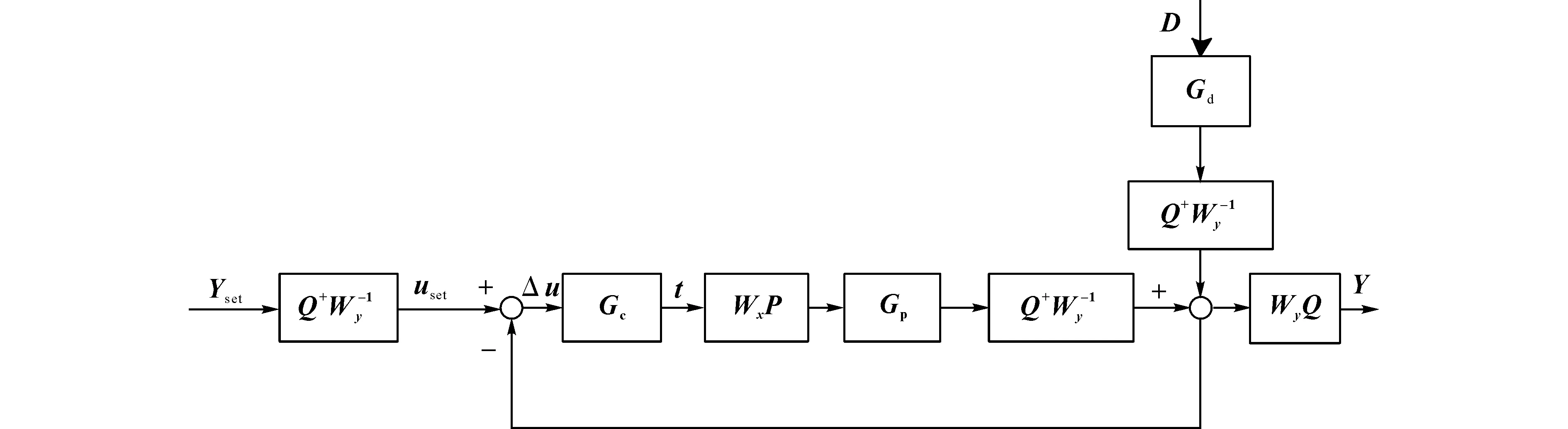
图1 Kaspar 等[12]提出的PLS控制框架Fig.1 PLS control framework proposed by Kaspar[12]
2 基于DyPLS框架的无静差预测控制器设计
2.1 基于DyPLS框架的状态空间MPC
在一些文献中,PLS被称为隐空间投影法(latent subspace project method)[20].该方法与子空间辨识法(subspace identification method)是不同的.对于MIMO系统来说,子空间辨识法是一种在原空间中辨识系统状态空间模型的方法,没有将原空间中的输入输出变量投影到潜变量空间中,也没有将MIMO系统解耦成多个SISO子系统.子空间辨识法不适用于本文设计的DyPLS框架下的状态空间MPC.
为了描述简便,作如下两点假设:假设式(4)中的模型误差ξr(k)为零;假设ARX模型时延系数na=nb.第r个潜变量ARX 模型(见式(4))可以转换成如下状况空间模型的形式[2]:
(6)
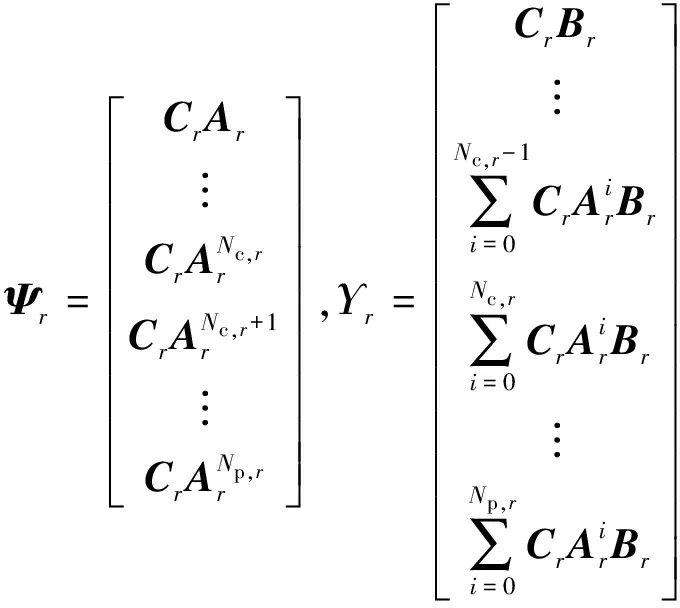
令Np,r和Nc,r分别表示控制器的预测时域和控制时域.Np,r的选取要大于模型的时滞部分,并覆盖动态响应的主要部分.Nc,r应满足Nc,r<=Np,r,且根据需求选取恰当的值以实现在控制灵敏度和稳定性间达到平衡的目的.模型输出ur的Np,r步前向预测为
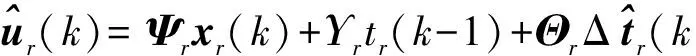
(7)
式中:
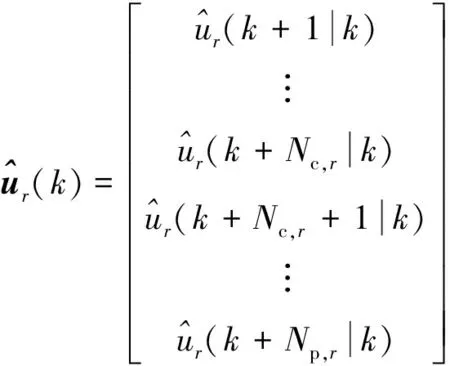

考虑如下有限时域二次目标函数:
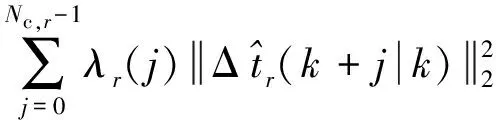
(8)
式中:uset,r为系统设定值在潜变量空间中的投影;δr(j)和λr(j)为权重系数序列;δr反映了对未来Np,r个不同时刻逼近的重视程度;δr(j)可以均取为1,表示对各个时刻的重视程度相同,或者适当增大某一个δr(j),以提高对某一时刻的重视程度.由PLS迭代提取潜变量的机制[11]可知,第一个潜变量对系统的描述程度最大,后提取的潜变量对系统的描述程度逐渐降低.对于r个不同潜变量控制器的权重δr均取1,表示对于不同潜变量控制器的重视程度遵循了各个潜变量描述系统的能力.控制增量权重λr的作用是对Δtr的剧烈变化加以适度限制.当不需要考虑控制器动作的剧烈程度时,可以令λr(j)为零或等于一个很小的值.当λr(j)增大时,相当于在控制器中加入一个软约束来抑制控制器的执行动作幅度,使系统的响应变慢,但会提高系统的鲁棒性.
将式(7)代入式(8)并求解最小化问题Jr, 可得得分向量的未来增量Δtr的最优化合集为
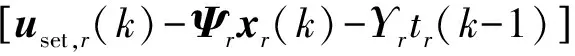
(9)
式中:δr=diag[δr(1),…,δr(Np,r)],λr=diag[λr(0),…,λr(Nc,r-1)],uset,r(k)=[uset,r(k+1),…,uset,r(k+Np,r)]T.
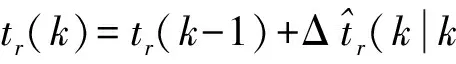

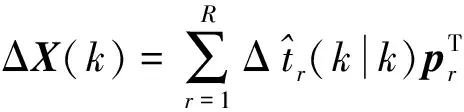
然后对ΔX进行积分得到下一时刻的系统输入值.
X(k)=X(k-1)+ΔX(k).
从式(7)可以看出,潜变量中的各个SISO控制器是相互独立的,已经实现了控制回路的匹配.该回路的匹配是在潜变量空间中实现的,与原空间中的输入输出变量无关,因此采用该方法可以处理非方系统的控制问题.对于各个潜变量的控制器来说,目标函数式(8)的计算是相互独立的,运算的复杂程度较传统的MIMO系统MPC算法低.
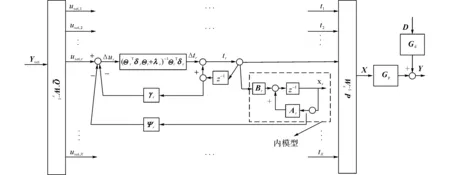
图2 基于DyPLS框架的状态空间MPC控制结构Fig.2 Structure of state space MPC control scheme in DyPLS framework
2.2 无静差MPC
通过引入扰动模型和状态观测器的方法来解决控制系统的稳态误差问题.在每个采样时刻,当前时刻或者未来时刻的扰动通常都无法测量.假设系统的扰动是常值扰动,扰动值在整个预测时域中为定值.以该扰动来估计状态空间模型的输出ur,得到增广的状态空间模型形式:
(10)
ur的Np,r步前向预测改写为
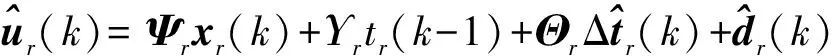
(11)
式中:
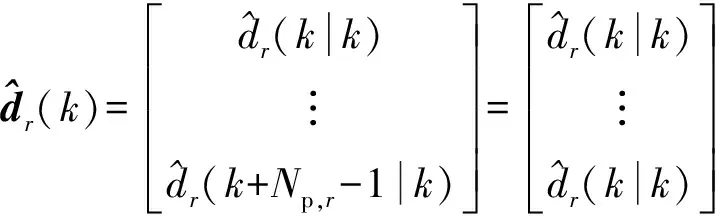

因为式(6)不能充分描述系统的状态,引入状态观测器对系统的状态进行估计[21].在引入状态观测器前,给出式(10)的能观测性条件.
命题1 增广状态空间模型式(10) 能观测,当且仅当(Ar,Cr)能观测,
(12)
证明:根据Hautus能观测性定理可知,增广状态空间模型式(10)是能观测的当且仅当∀λ,式(13)是行满秩的.
(13)
当且仅当(Ar,Cr)能观测,式(13)的第一行是线性不相关的.λ决定了式(13)第二行的线性相关性.当且仅当λ≠1时,式(13)的第二行是线性不相关的.根据Hautus能观测性定理可知,式(10)的能观测性条件只需要满足λ≠1,即式(12)成立.证毕.
增广状态空间模型式(10)的状态观测器可以定义为
xr(k+1)=Arxr(k)+Brtr(k)+Brdr(k)+
(14)
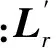
卡尔曼滤波器的方法要求系统和测量的噪声满足高斯分布,并通过噪声的协方差来计算增益矩阵.在潜变量空间中使用卡尔曼滤波器,需要知道原空间中数据投影到潜变量空间后噪声协方差的变化情况.令σr表示第r个潜变量的得分向量的噪声方差.
命题2σr是矩阵Q+的第r列向量元素的和.
证明:由式(1)可知,得分矩阵U的计算公式为
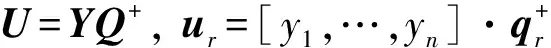

由式(11)可得,得分向量的未来增量Δtr的最优化合集为

(15)
利用式(14)的状态变量代替式(15)中的xr,可得Δtr的求取公式.
3 仿真研究
Jerome-Ray精馏塔模型是一个具有右半平面零点的最小相位系统[23].许多控制算法采用该模型进行验证.系统的模型为

(16)
为了模拟实际系统存在扰动的运行情况,给系统模型加入如下的扰动模型[24]:

(17)

图3 用于建立DyPLS模型的输入输出数据Fig.3 Input and output data to model DyPLS system
为了验证该方法的有效性,采用基于状态空间MPC (state space MPC, SMPC)、DyPLS框架下的状态空间MPC(state space MPC in DyPLS, SMDP)和无静差SMDP(offset free state space MPC in DyPLS, OSMDP) 3种方法进行对比仿真实验.为了建立系统的DyPLS模型,选择设定值为[-1,1]的随机阶跃信号激励系统.加入一个零均值方差为0.5的白噪声信号作为扰动信号的输入.用于激励系统模型的信号如图3所示.利用同样参数生成另外一组随机信号以验证建模的有效性,建模的结果如图4所示.
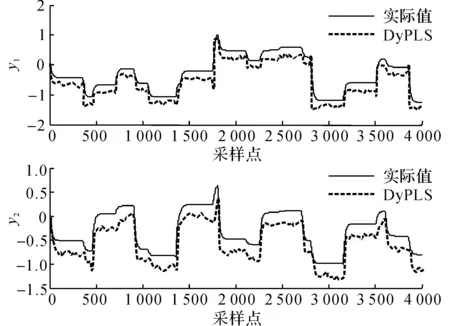
图4 DyPLS建模结果Fig.4 Modeling results of DyPLS
为了确定所提取的潜变量个数,定义如下性能指标:

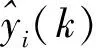

图5 无扰动时SMPC的仿真结果Fig.5 Simulation result of SMPC without disturbance
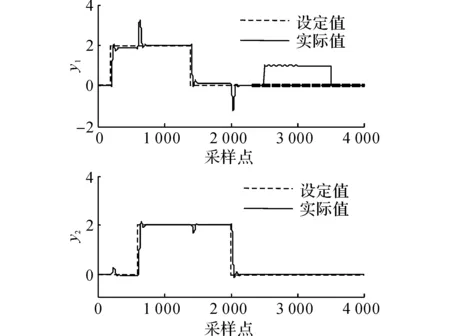
图6 无扰动时SMDP的仿真结果Fig.6 Simulation result of SMDP without disturbance

图7 无扰动时OSMDP的仿真结果Fig.7 Simulation results of OSMDP without disturbance
为了验证控制器的控制性能,进行4 000步的仿真.在第200~1 400步和第600~2 000步时分别给y1和y2一个幅值为2的阶跃信号.在第2 500~3 500步时,给y1一个不可测的恒值扰动信号.仿真结果如图5~7所示.为了验证3种方法在系统存在扰动时的控制性能,对扰动模型Gd加入一个零均值方差为0.5的白噪声信号作为扰动信号的输入,并重新进行上述的4 000步仿真实验.仿真结果如图8~10所示.仿真中3种方法的控制时域和预测时域参数如表1所示.表中,tc为计算时间.

图8 存在扰动时SMPC的仿真结果Fig.8 Simulation results of SMPC with disturbance

图9 存在扰动时SMDP的仿真结果Fig.9 Simulation results of SMDP with disturbance
Tab.1 Parameter for three control algorithms and computing time
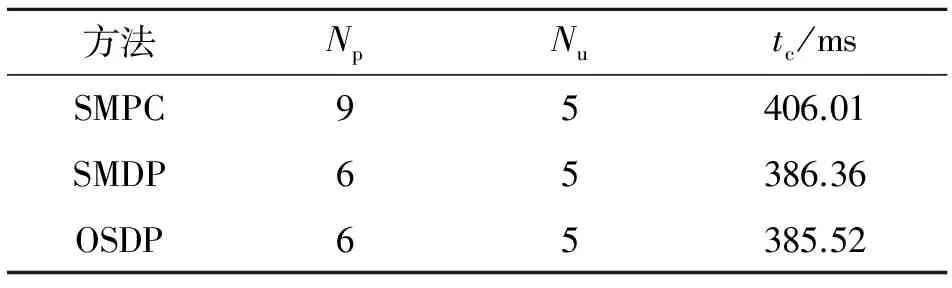
方法NpNutc/msSMPC95406.01SMDP65386.36OSDP65385.52
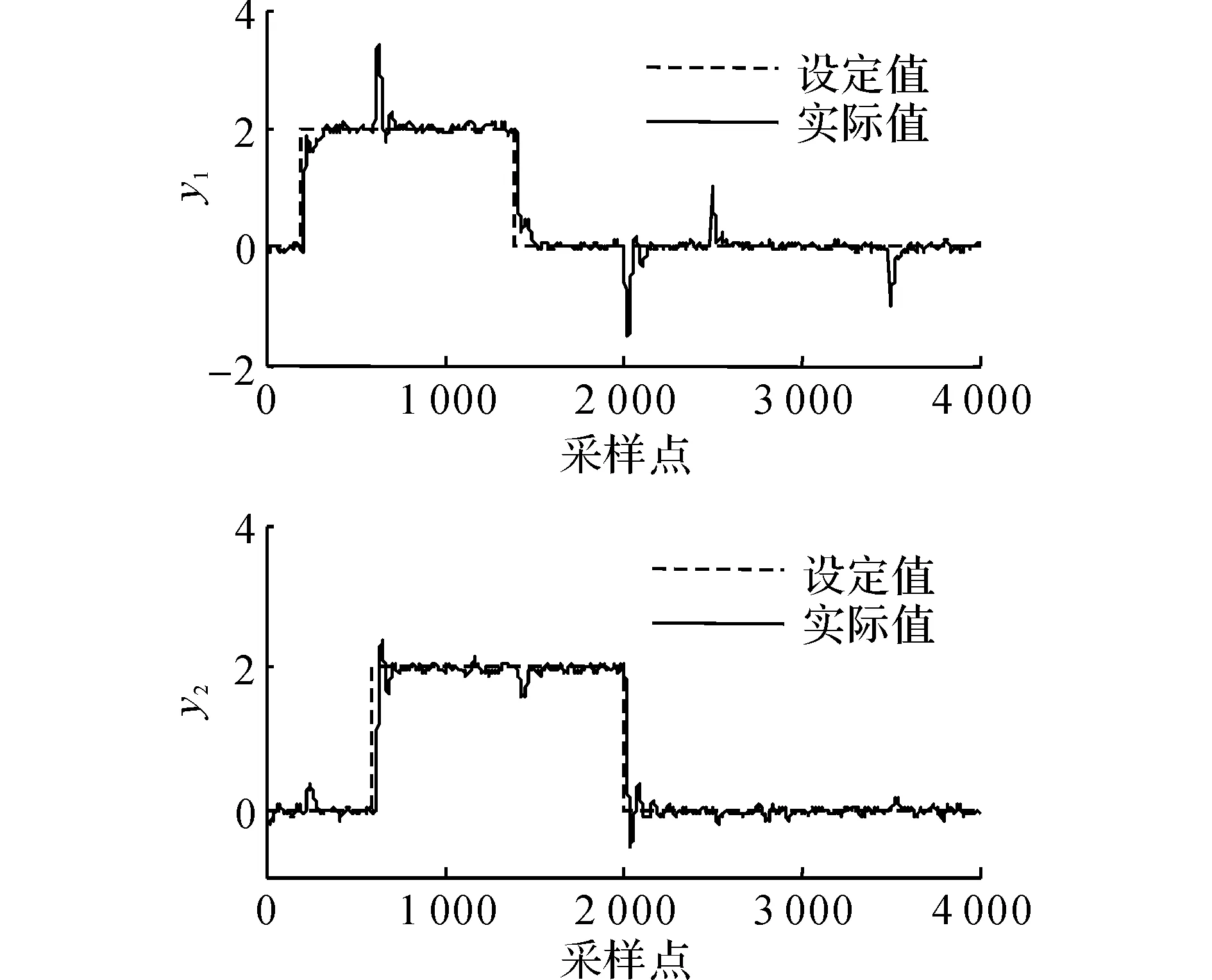
图10 存在扰动时OSMDP的仿真结果Fig.10 Simulation results of OSMDP with disturbance
由于预测模型和系统模型存在偏差,SMPC和SMDP的控制方法存在稳态误差.OSDP由于在DyPLS的内模型中引入了状态观测器使模型失配得以补偿,取得了无静差的跟踪性能.

4 结 语
本文提出基于DyPLS框架的具有无静差跟踪特性的状态空间模型预测控制方法.该方法具有以下5个特点:1)DyPLS框架下的状态空间模型比MIMO状态空间模型的结构简单;2)可以将MIMO系统解耦成多个SISO子系统;3)可以自动进行控制回路的匹配;4) 能够处理非方系统的控制问题;5) 对于维数较大的系统来说,采用DyPLS方法可以降低系统维数.由于DyPLS模型和系统的实际模型之间存在偏差,控制结果往往存在静差.为了解决该问题,将状态空间模型增广为包含恒值扰动模型的形式,并引入状态观测器估计系统的状态.为了利用卡尔曼滤波器求取观测器的增益矩阵,分析原变量空间投影到潜变量空间后,数据的方差关系.该方法的使用将提高DyPLS模型与系统模型匹配精度的问题转化为估计潜变量空间中各得分向量的方差问题,从而使问题得以简化.仿真的结果表明,OSDP能够取得很好的无静差跟踪设定值的控制性能,并能够抑制系统中存在的不可测扰动.
[1] MUSKE K R, RAWLINGS J B. model predictive control with linear-models [J]. Aiche Journal, 1993,39(2): 262-287.
[2] LJUNG L. System identification-theory for the user. prentice hall information and system sciences series [M]. 2nd ed. Upper Saddle River: Prentice Hall,1999:79-99.
[3] HUUSOM J K, POULSEN N K, JORGENSEN S B, et al. Adaptive disturbance estimation for offset-free SISO model predictive control [C]∥ Proceedings of the American Control Conference. New York:[s.n.], 2011:2417-2422.
[4] MUSKE K R, BADGWELL T A. Disturbance modeling for offset-free linear model predictive control [J]. Journal Of Process Control, 2002, 12(5): 617-632.
[5] MORARI M, MAEDER U. Nonlinear offset-free model predictive control [J]. Automatica, 2012, 48(9):2059-2067.
[6] BORRELLI F, MORARI M. Offset free model predictive control [C]∥ Proceedings of Ieee Conference onDecision And Control. New Orleans: [s.n.], 2007: 4663-4668.
[7] MAEDER U, BORRELLI F, MORARI M. Linear offset-free model predictive control [J]. Automatica, 2009, 45(10): 2214-2222.
[8] MAEDER U, MORARI M. Offset-free reference tracking with model predictive control [J]. Automatica, 2010, 46(9): 1469-1476.
[9] BETTI G, FARINA M, SCATTOLINI R, et al. An MPC algorithm for offset-free tracking of constant reference signals [C]∥ 2012 IEEE 51st Annual Conference on Decision And Control. Maui: IEEE, 2012:5182-5187.
[10] BETTI G, FARINA M,SCATTOLINI R. A robust MPC algorithm for offset-free tracking of constant reference signals [J]. IEEE Transactions on Automatic Control, 2013, 58(9): 2394-2400.
[11] KASPAR M H, RAY W H. Chemometric methods for process monitoring and high-performance controller design [J]. AIChE Journal, 1992, 38(10): 1593-1608.
[12] KASPAR M H,RAY W H. Dynamic PLS modelling for process control [J]. Chemical Engineering Science, 1993, 48(20): 3447-3461.
[13] CHEN J, CHENG Y C, YEA Y. Multiloop PID controller design using partial least squares decoupling structure [J]. Korean Journal of Chemical Engineering, 2005, 22(2): 173-183.
[14] LAUR D, MART NEZ M, SALCEDO J V, et al. PLS-based model predictive control relevant identification: PLS-PH algorithm [J]. Chemometrics and Intelligent Laboratory Systems, 2010, 100(2): 118-126.
[15] HU B, ZHENG P, LIANG J. Multi-loop internal model controller design based on a dynamic PLS framework [J]. Chinese Journal of Chemical Engineering, 2010, 18(2): 277-285.
[16] HU B, ZHAO Z, LIANG J. Multi-loop nonlinear internal model controller design under nonlinear dynamic PLS framework using ARX-neural network model [J]. Journal of Process Control, 2012, 22(1): 207-217.
[17] LV Y, LIANG J. Multi-loop constrained iterative model predictive control using ARX-PLS decoupling structure [J]. Chinese Journal of Chemical Engineering, 2013, 21(10): 1129-1143.
[18] WOLD S, SJOSTROM M, ERIKSSON L. PLS-regression: a basic tool of chemometrics [J]. Chemometrics And Intelligent Laboratory Systems, 2001, 58(2): 109-130.
[19] LAKSHMINARAVANAN S, SHAH S L, NANDAKUMAR K. Modeling and control of multivariable processes: dynamic PLS approach [J]. AIChE Journal, 1997, 43(9): 2307-2322.
[20] MORI J, YU J. A quality relevant non-gaussian latent subspace projection method for chemical process monitoring and fault detection [J]. Aiche Journal, 2014,60(2): 485-499.
[21] MACIEJOWSKI J. M. Predictive control: with constraints [M]. Upper Saddle River: Prentice-Hall,2002.
[22] HUUSOM J K, POULSEN N K, JORGENSEN S B, et al. Tuning SISO offset-free model predictive control based on ARX models [J]. Journal of Process Control, 2012, 22(10): 1997-2007.
[23] JEROME N F, RAY W H. High-performance multivariable control strategies for systems having timedelays [J]. Aiche Journal, 1986, 32(6): 914-931.
[24] ZHAO Z, HU B, LIANG J. Multi-loop adaptive internal model control based on a dynamic partial least squares model [J]. Journal Of Zhejiang University: Science A, 2011, 12(3): 190-200.
Multivariable offset free model predictive control in dynamic PLS framework
JIN Xin, LIANG Jun
(CollegeofControlScienceandEngineering,ZhejiangUniversity,Hangzhou310027,China)
An offset free model predictive control (MPC) in the DyPLS framework was proposed in order to deal with the problem of system offset which was caused by mismatch between actual plant and dynamic partial least square (DyPLS) model. State space MPC was extended into the DyPLS framework. The state space model was used in inner model to describe the system dynamic, and state space MPC controller was designed. The state of inner model was as the feedback of the control system. This state can’t describe the real system state and results in offset due to model/plant mismatch. A disturbance model was introduced in the inner state space model in order to solve the problem. A state observer was used to estimate the error between the inner model and system output. Observability condition of augmented model was given. The covariance that the original space data were projected to the latent variable space was analyzed in order to calculate the gain matrix of the observer with Kalman filter. The method used the system output as feedback in the control scheme. The offset free tracking was guaranteed and unmeasured step disturbance can be rejected. The simulation results based on Jerome-Ray distillation column model demonstrated the effectiveness of proposed method.
partial least square; model predictive control (MPC); state space model; offset free control
2015-11-09. 浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
国家自然科学基金资助项目(61174114,U1509203);教育部高校博士点基金优先领域资助项目(20120101130016);浙江省公益性技术应用研究计划资助项目(2014C31019).
金鑫(1986—),男,博士生,从事预测控制方法的研究.ORCID: 0000-0002-1904-9424.E-mail: xjin@iipc.zju.edu.cn 通信联系人:梁军,男,教授.ORCID: 0000-0003-1115-0824.E-mail: jliang@iipc.zju.edu.cn
10.3785/j.issn.1008-973X.2016.04.021
TP 273
A
1008-973X(2016)04-0750-09
