基于局部强化最小二乘回归子空间分割的基因表达数据聚类

简彩仁，翁谦

（1．厦门大学嘉庚学院，福建漳州363105；2．福州大学数学与计算机科学学院，福建福州350116）

基于局部强化最小二乘回归子空间分割的基因表达数据聚类

简彩仁1，翁谦2

（1．厦门大学嘉庚学院，福建漳州363105；2．福州大学数学与计算机科学学院，福建福州350116）

利用局部约束协同表示法改进最小二乘回归子空间分割方法，提出局部强化最小二乘子空间分割方法（LSLSR）。该方法通过近邻样本的协同作用强化重构系数使得LSLSR有更好的抗噪能力，结果表明该方法有较高的聚类准确率。

局部强化；最小二乘回归子空间分割；基因表达数据；聚类

聚类是模式识别研究的重要方向之一，其目标是将未知类别的数据根据某种特性分成不同的簇，使得每个簇都有相似的特点。聚类方法多种多样，传统的聚类方法：(1)基于划分的聚类方法，比如k-means算法[1]；(2)基于层次的聚类算法，比如BIRCH算法[2]；(3)基于密度的聚类算法，比如DBSCAN算法[3]；(4)基于网格的方法，比如STING算法[4]。传统的算法不断改进和发展，出现了模糊聚类，谱聚类等。谱聚类[5]是一种基于图论的聚类算法，适合于各种形状的数据集的聚类，因而得到广泛应用。谱聚类的关键是构造图拉普拉斯矩阵。本文主要研究谱聚类。

子空间分割(subspace segmentation)是近年来模式识别研究的热点问题之一，已经广泛应用在图像分割、人脸识别和机器视觉等领域[6-8]，并且在基因表达数据识别中也有广泛应用[9]。子空间分割方法的目标是将数据集分割成不同的簇。子空间分割的主要思想是，假设每一个数据集都是从混合子空间采样的，其目标是将数据集分割成几个簇，每一个簇对应于一个子空间[8]。子空间分割方法多种多样，文献[8]将子空间分割方法分为4类:代数方法、迭代方法、统计方法和谱聚类方法。低秩表示子空间分割方法[7]和最小二乘回归子空间分割方法[8]是基于谱聚类的子空间分割方法的典型代表，但是这些方法存在易受噪声样本影响的不足。

本文的研究旨在改进子空间分割方法易受噪声样本影响的不足。模式识别的方法不仅要求有较好的识别能力，还要有较好的抗噪能力。文献[10]的局部约束协同表示法表明通过局部强化不仅可以提高图像识别的准确率，而且可以提高抗噪声能力。本文借鉴该思想改进最小二乘回归子空间分割方法，提出局部强化的最小二乘回归子空间分割方法。

1相关理论

子空间分割是谱聚类的一种，其核心是构造样本的相似矩阵。子空间分割的目标是将数据集分割成对应于不同子空间的簇。

定义[8]子空间分割(subspace segmentation)

给定一个数据向量集合X=[x1，x2，…，xn]∈Rm×n其中，m是特征个数，n是样本个数。假设X从K个子空间的并集中抽样{Si}Ki=1，子空间分割的目标是将数据根据样本采样的子空间将样本分割成不同的簇。

子空间分割方法有许多类型，比如代数方法，迭代方法等[8]。基于谱聚类的子空间分割是近年来的研究热点。比如，低秩表示子空间分割（low rank representation，LRR）[7]和最小二乘回归子空间分割（least square regression，LSR）[8]是基于谱聚类的子空间分割方法的典型代表。基于谱聚类的子空间分割方法的核心问题是求解仿射矩阵Z。仿射矩阵Z中的每个元素Zij用来度量样本xi和xj的相似度，比如0就可以用来构造仿射矩阵Z。然而仅仅考虑两个样本间的距离不能很好地刻画数据的本质特征[10]。低秩表示子空间分割和最小二乘回归子空间分割从全局考虑了样本间数据的关系可以很好地克服这样的不足。

低秩表示子空间分割和最小二乘回归子空间分割方法将每个样本点xi表示为其它样本点的线性组合接着用（）/2表示xi和xj之间的相似度。这两种方法的不同在于表示系数的惩罚函数。

低秩表示子空间分割[9]的求解目标是秩最小问题，但是这是NP难的，文献[7]将其退化成一个凸问题

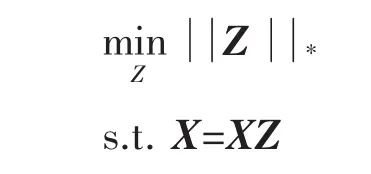
最小二乘回归子空间分割[8]方法本质上是岭回归在子空间分割中的应用，其目标是

利用低秩表示子空间分割和最小二乘回归子空间分割方法可以得到仿射矩阵，最后可以利用标准分割（normalized cuts）[11]方法实现聚类。这两种方法可以方便的求出仿射矩阵，但是容易受到噪声的干扰。

2局部强化最小二乘回归子空间分割

最小二乘回归子空间分割方法具有解析解，本文将最小二乘回归子空间分割方法进行改进.通过强化局部样本对子空间分割的影响，提出局部强化最小二乘回归子空间分割（local strengthen least square regression，LSLSR）.

2.1目标函数

利用数据集X∈Rm×n线性重构某个样本y∈Rm×1，即

最小二乘回归子空间分割方法[8]所研究的岭回归模型

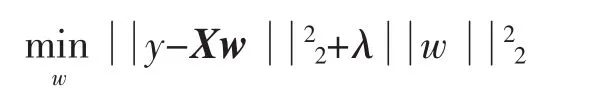
该方法容易受到噪声样本的影响。

基于这一不足，强化局部样本对子空间分割的影响提出局部强化最小二乘回归子空间分割方法如下，

其中，SL是局部强化项，代表局部样本对子空间分割的影响，γ是正则参数。局部强化项SL的定义是多种多样的[10]。将近邻样本视为局部样本，用文献[10]的方法定义如下的局部强化项

其中bi∈N（y）是样本y的近邻样本，K表示近邻样本的个数,SL反映了局部样本对重构系数的影响。由此，得到如下的目标函数

公式(1)的第一项是样本重构项，第二项是局部强化项，参数γ（0＜γ＜1）用于平衡样本重构项和局部强化项，最后一项是岭回归惩罚项，γ＞0是正则参数γ＞0。

2.2目标函数求解

本节研究目标函数的求解，令目标函数(1)为O（w），则

这里Tr（X）表示求迹，并且应用了Tr（X）=Tr（XT）和Tr（XY）=Tr（YX）。对w求导得

2.3局部强化最小二乘子空间分割算法

首先，对每个样本通过(2)的求解得到该问题的解w，进而可以构造矩阵Z*=（wi）n得到仿射矩阵接着应用谱聚类方法：标准分割方法（normalized cuts）[11]对仿射矩阵进行分割.将这一过程归纳为如下的局部强化最小二乘子空间分割算法（local strengthen least square regression，LSLSR）

算法：局部强化最小二乘子空间分割算法（LSLSR）；

Input：数据矩阵X，类数k，局部样本数量K，正则参数λ，γ；

Output：k个类簇；

Step1：对于每个样本通过(2)解决问题(1)得到解w；

Step2：将n(为样本个数)个w构成矩阵Z*计算仿射矩阵（

Step3：应用标准分割方法将数据分成个子空间。

3实验及结果分析

本节从聚类准确率的角度来验证局部强化最小二乘回归子空间分割算法（LSLSR）对基因表达数据聚类的有效性.对比方法为经典的子空间分割方法：低秩表示子空间分割方法（LRR）和最小二乘回归子空间分割方法（LSR），传统的聚类方法:K均值聚类（K-means）和层次聚类法（HC）。聚类准确率的定义[12]为：对给定样本，令ri和si分别为聚类算法得到的类标签和样本自带的类标签，那么准确率的计算公式为

其中n为样本总数，δ（x，y）是一个函数，当x=y时，值为1，否则为0,map（ri）是一个置换函数，将每一个类标签ri映射成与样本自带的类标签等价的类标签。

3.1数据描述

选用6个常用的基因表达数据集来验证LSLSR的有效性，这些数据来源于文献[13]的研究，将其总结成表1。

所有数据集都标准化为具有单位L2范数，即用式(3)标准化，

其中x表示一个样本。

表1数据集描述

3.2实验结果与分析

实验过程中，LSLSR、LSR、LRR等子空间分割方法存在参数设置问题，采用搜索策略来设置参数：LSLSR、LSR、LRR这3种方法的正则参数λ均采用统一的取值0.0001,0.001,0.01,0.1,1；LSLSR的正则参数的取值为0.1到0.9;局部样本数量取值为2到10。为避免随机性，每种方法运行10次，取聚类平均值。表2以聚类平均值±方差的方式给出实验结果。

表2聚类准确率

由实验结果可以看出，LSLSR可以取得较好的聚类准确率。对比所有方法，在全部数据集上LSLSR的聚类准确率都是最高的。

LSLSR方法与经典的子空间分割方法LSR和LRR对比，可以发现，LSLSR的聚类准确率显著高于后两者。这表明LSLSR考虑了局部样本可以更好地适应基因表达数据的多噪声特点，具有更好的鲁棒性。因此，本文提出的局部强化思想是可以改进子空间分割方法的聚类性能的。

对比传统的K-means和层次聚类两种方法，LSLSR的优势依然明显.这说明传统的聚类方法不能很好地适应高维数小样本多噪声的基因表达数据的聚类。造成这样的原因是基因表达数据的高维数小样本特点导致距离度量不准确，难以取得理想的聚类结果.这一实验结果也反映了LSLSR比传统聚类方法更加适合基因表达数据的聚类。

3.3参数讨论

局部强化最小二乘子空间分割算法（LSLSR）有3个重要参数：局部样本数量和两个正则参数。文献[8-9]的研究最小二乘回归子空间分割方法在正则参数较小时会有较好的聚类结果，以这一研究为依据，本文取λ=0.01，讨论局部样本数量和正则参数对实验结果的影响。图1给出了不同参数下LSLSR的聚类准确率。

图1 K、γ不同时LSLSR在6个数据集上的聚类准确率

从图1，可以发现不同的实验参数对聚类准确率会产生影响.当较小时，LSLSR的聚类准确率较高，这反映了在聚类过程中，更加强调原样本的影响，但是局部样本也对实验结果产生了影响。当较小时，LSLSR有较好的聚类准确率，随着近邻数量的增加准确率会下降（SRBCT除外），这符合基因表达数据的小样本多噪声的特点，进一步说明LSLSR有较好的抗噪能力。

4结束语

局部强化最小二乘子空间分割算法（LSLSR），通过局部样本的限制加强了近邻样本对样本聚类的影响，可以较好地提高样本的抗噪能力。实验结果表明LSLSR是一种有效的聚类算法。对于研究基因表达数据聚类，LSLSR聚类效果明显优于经典的子空间分割方法LRR和LSR。LSLSR需要分别求取每个样本的重构系数，时间消耗比LSR多，但是LSLSR有解析解，并且基因表达数据的低维数特点，因此不会减弱LSLSR的实用性.LSLSR的有3个重要参数，如何自适应的选择参数需要进一步的研究。

［1］HAMERLY G，ELKAN C．Alternatives to the k－means algorithMthat find better clusterings［C］／／International Con-ference on Information and Know ledge Management，2002：600－607．

［2］ZHANG T，RAMAKRISHNAN R，LIVNY M．BIRCH：an efficient data clusteringmethod for very large databases［J］．AcMSigmod Record，1999，25：103－114．

［3］BIRANT D，KUT A．ST－DBSCAN：a n algorithMfor clustering spatial–temporal data［J］．Data＆Know ledge Engineering，2007，60（1）：208－221．

［4］WANG W，YANG J，MUNTZ R R．STING：a statistical information grid approach to spatialdataMining［C］//Proceedings of the 23rd International Conference on Very Large Data Bases．[s.l.]：Morgan Kaufmann Publishers Inc．，1997：186－195．

［5］NG A Y，JORDAN MI，WEISSY Y．On spectral clustering：analysis and an algorithm［J］．Proceedings of Advances in Neural Information Processing Systems，2001，14：849－856．

［6］ELHAMIFAR E，VIDAL R．Sparse subspace clustering［C］//Proceedingsof 23rd IEEE Conference on Computer Vision and Pattern Recognition，2009：2790－2797．

［7］LIU G，LIN Z，YU Y．Robustsubspace segmentation by low－rank representation［C］//Proceedingsof the27th InternationalConference on Machine Learning，2010：663－670．

［8］LU C Y，MIN H，ZHAO Z Q，et al．Robust and efficient subspace segmentation via least squares regression［C］//Proceedingsof the 12th European Conference Computer Vision，2012：347－360．

［9］CHEN X，JIAN C．Gene expression data clustering based on graph regularized subspace segmentation［J］．Neurocomputing，2014，143（16）：44–50．

［10］PENG X，ZHANG L，YIZ，etal．Learning locality－constrained collaborative representation for robust face recognition［J］．Pattern Recognition，2014，47（9）：2794–2806．

［11］S HI J，MALIK J．Normalized cuts and image segmentation［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（8）：888－905．

［12］CAID，HEX，WU X，etal．Non－negativematrix factorizationonmanifold［C］．//Proceedingsof the 8th IEEE International Conference on Data Mining，2008：63－72．

［13］STATN IKOV A，TSAMARDINOS I，DOSBAYEV Y，et al．GEMS：a systeMfor automated cancer diagnosis and biomarker discovery from Microarray gene expression data［J］．International journal ofmedical informatics，2005，74（7）：491－503．

（责任编辑：朱联九）

Gene Expression Data Clustering Based on Local Strengthen Least Square Regression Subspace Segmentation

JIAN Cai-ren1,WENG Qian2

（1.Tan Kah Kee Colleage,Xiamen University,Zhangzhou,363105，China;2.College of Mathematics and Computer Science,Fuzhou University,Fuzhou,350116，China）

Subspace segmentation segments the data set into different clusters,which is broadly used in pattern recognition.Authors improve least squares regression subspace segmentation by using locality-constrained collaborative representation.Local strengthen least square regression subspace segmentation is proposed.The proposed method strengthens the reconstruct coefficientby using neighbor data samples,so that LSLSR has the ability to robustagainst various corruptions and occlusions.The experimental results show that themethod can achieve a high clustering accuracy.

local strengthen;leastsquare regression subspace segmentation;gene expression data;clustering

TP18

A

1673-4343（2016）06-0001-07

10．14098／j．cn35－1288／z．2016．06．001

2016-06-08

福建省科技创新平台建设项目(2009J1007)；福建省教育厅科技项目(JK2010001）

简彩仁，男，福建永定人，助教。主要研究方向：数据挖掘、模式识别。