数学考试的是与非—关于考试之于学习效果影响的分析

江苏省海门市四甲初级中学(226141)曹群

数学考试的是与非—关于考试之于学习效果影响的分析

江苏省海门市四甲初级中学(226141)曹群

在初中数学学习过程当中,考试对于学生们来讲可以说是家常便饭了.为了充分巩固和提升学生对知识的掌握情况,很多学校都有周周练,而且每个章节学习之后还有单元检测,单元提高训练等.还会有阶段考试,定期还会有期中、期末等常规性重要考试.很多学生对于数学考试并没有太多好感,有的甚至将之视为一种压力和负担.这不禁引发了教师们的思考:考试对于数学教学来讲真的是没有意义的吗?其实不然,教师如何在教学过程中优化考试的内容的命制,优化我们的评价形式,我们完全可以提升考试的价值和其深远的教育价值.笔者尝试着结合自己的实践研究,通过对各类数学考试的内容及效果进行分析,笔者总结归纳出了数学考试对于学习效果的几种积极影响:

一、通过考试,重温基础知识

每一次数学考试中,试题的难度都是参差不齐的.在这之中,基础性习题占据了很大的比重.对于一次考试的设计来讲,笔者认为,基础性习题的设置意义远远大于拔高类习题.对于不同知识程度的学生来讲,夯实知识基础都是取得学习进步的关键.因此,这个学习重点有必要通过考试的方式体现出来,并以试题的形态加以强调.

例如,在函数章节的测验当中,我设计了这样一道题目:如图当中所表示的是函数y= ax2+bx+c的图象.那么,由此能否判断出方程ax2+bx+c+2=0的根的情况呢?(A)方程的两个实根异号;(B)方程的两个实根同号;(C)方程的两个实根相等; (D)方程没有实根.这道题目显然是从根与系数这一基础知识出发来设计的.表面看来难度不大,但想要把它答对,仍然需要学生们对根与系数的关系与特点的内容有一个准确把控.这道题目的出现,让很多忽视这部分基础内容的学生重新加强了注意,在对这部分知识进行复习回顾时也更加目标明确了.

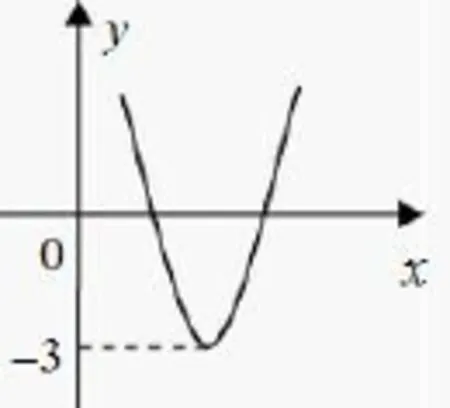
图1　

以基础知识为内容设计试题,听起来虽然降低了整次考试的难度,实则提升了考试存在的价值.其深层的优化价值可以达成以下三点:(1)关注基础,教师通过这种类似于单元检测的考试形式引领学生定期的巩固和评价自己对知识与技能的掌握情况.(2)服务后续.数学的学习表现出较为明显的递进性,很多新知识与技能的学习都依托于学生已学知识与技能的扎实度,只有让学生拥有扎实的基础才能有效的开展后续的学习和拓展,扎实的基础是学生是初中数学有效学习开展的前提,更是广大师生们应当转变的教学理念.(3)引领思想.从考试行为让学生体验的,只有脚踏实地的走好每一步,才能走的更远走的更稳,无论是数学的学习还是其他科目的学习,或是走向社会后的做人做事,都需要大家脚踏实地的走好每一步.因此,常态好的基础试题精选和精练是必须的,从行为上引起学生对自己知识薄弱环节的重视,并从意识上引起学生的重视.

二、通过考试,强化独立思考

数学学习虽然常常会在合作与讨论的氛围下进行,但是,知识能力的掌握最终是要归于学生个人的.这也就是我们在这里所谈到的独立思考能力.越来越多的合作教学机会,让很多学生形成了一种“自己不会问别人”的思维习惯,这种所谓的“合作”让学生养成思维的惰性,这明显是不可取的.为了让学生将合作学习与独立思考的界限划清,真正让学生在自我思维的独立中训练、提升学生的思维能力,考试这种促使学生独立思考的教学形式也就显得必不可少了.

例如,在一次二次函数内容的考试中,我设计了如下题目:如图所示,点A与点C是二次函数y=ax2+bx+3的图象与横轴的两个交点,且该图象与纵轴的交(点是)B.其中,点A的坐标是且△AOB与△BOC相似.(1)请依次求出点C的坐标、∠ABC的大小和函数y=ax2+bx+3的表达式. (2)是否能够在线段AC上找到一个点M(m,0),能够让以MB为直径的圆交BC于点P(不与点B重合),并使得点C、O、P围成一个等腰三角形?在这个问题中,第二问的解答是具有一定难度的.很多学生一开始感到分析过程有些混乱.但在考试氛围的驱动下渐渐发现,这之中是有规律可循的.当我们按照CP=OC、CP=OP、OC=OP三种情况分别展开思考时,思路便会瞬间明朗起来.学生们的独立思考能力也在这个过程中得到了有效强化.

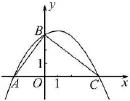
图2　

在考试进行中,学生们在外力的作用下实现了一个完全独立的思考环境,也在这种压力之下被激发出了思考的动力.在逐个分析试题时,学生们不得不将自己的知识能力全部调动起来,妥善运用知识方法,将解题效果发挥到最佳.适当增加数学考试的数量,对于强化学生们的独立思考能力与习惯是很有好处的,能借此为学生营造一个较为安静的独立思考问题的氛围,有效的服务于学生独立思考能力的提升,服务于学生思维能力的提升.

三、通过考试,明确思维过程

在一次考试的最后,教师们总会设计一些略有难度的试题,来提升整次考试的思维训练效果,这对于初中数学教学来讲也是十分必要的.在落实知识基础的前提下,适当地拔拔高,以考试的形式表现出来,能够更好地促进学生们的知识水平提升,将数学学习效果推进到新的高度.这些思维过程的深入体验让学生明确了思维方向、理顺了思维过程,渐渐的养成良好的思维习惯,有效的提升了学生的思维能力.

例如,我曾在一次考试中设计了这样一道考题:在△ABC中,∠B是直角,AB边的长为12cm,BC边的长为24cm.现有动点P和Q,分别从点A和点B开始,沿着AB、 BC的方向,以2cm/s和4cm/s的速度运动,且不与点B和点C重合.那么,若两动点的出发时间相同,则需要运动多长时间,使得四边形APQC的面积取得最小?学生们在解题过程中发现,仅从字面上来分析,是很难找到题目中隐藏的数学关系的.当大家将图形表示出来后(如图),虽然只是简单一画,思路却瞬间明朗了.在明确题意的基础上,函数关系也就自然顺利得出了.这个数形结合的思维过程,让学生们找到了解答复杂数学问题的新方法.

在较为复杂的数学问题面前,学生们不仅需要严谨的知识理论作为保障,还要着眼于思维方式的清晰运用.这类问题的分析,使得数学思想方法的适用成为了必然.也正是通过将这类问题融入于考试当中,才让数学思维这个主题引发了学生们的足够关注,并成为了初中数学学习效果提升的有力推手.

不得不说,数学考试的严肃形式常常会从心理上给学生们带来不小的学习压力,但这并不妨碍其对于学习效果的显著促进作用的发挥.数学考试不同于平时的知识学习,它建立在学生们对于知识内容一定的理解基础上,具有阶段总结与提升的效果.因此,从考试当中所收获的学习效果往往是升华性的.数学考试以一种无形的方式实现了对学生数学知识能力的高阶教学,完成了从知识内容到思维能力的全面强化.因此,初中阶段的数学考试不容忽视,且应当成为推进教学实效提升的重要途径.