改进的正方形NAM二值图像表示方法

宫海晓，贺 杰，郭 慧

(1.2.3.梧州学院 信息与电子工程学院，广西 梧州 543002)



改进的正方形NAM二值图像表示方法

宫海晓1，贺 杰2，郭 慧3

(1.2.3.梧州学院 信息与电子工程学院，广西 梧州 543002)

借助非对称逆布局思想，提出一种改进的正方形NAM二值图像表示方法，对其存储结构、数据量进行了理论分析，同时选取部分常用的二值图像，对该方法进行了实验测试。结果表明：与正方形NAM和线性四元树图像表示方法相比，该方法有效地降低了图像的存储空间、减少了子模式的数据量。

NAM；正方形；线性四元树；子模式

随着多媒体技术的快速发展，越来越多的图像数据需要计算机进行处理，由于图像数据量剧增，使得图像数据的存储和传输面临极大挑战。如何高效地表示图像，降低图像数据并提高图像的处理速度成为了图像处理、模式识别和计算机图形学等领域中一个非常重要的问题，也是目前最活跃的研究内容之一[1]。目前常用的图像表示方法是基于分层结构的线性四元树(LQT)表示方法[2]和基于非对称逆布局模型(NAM)的表示方法[3]。线性四元树由于强调图像分割的对称性，所以产生的节点数量较多，在图像处理效率上难以达到最佳，而陈传波教授提出的NAM图像表示方法强调图像分割的非对称性，因此在提高图像的处理速度、降低图像的存储空间等方面都取得了显著的成效。后续研究者在NAM的思想上，通过选取矩形、三角形等不同的子模式[4-5]，实现了多种图像表示方法，本文在正方形NAM表示方法(SNAM)的基础上[6]，对其存储结构、残渣模式等方面加以优化改进，提出了改进的正方形NAM二值图像表示方法，即ISNAM。

1算法的改进和描述

1.1算法的改进

虽然SNAM算法已经在理论和实验方面均已证明优于经典的线性四元树图像表示方法，但该方法仍然存在进一步优化的空间，主要表现在以下三个方面。

1.1.1残渣模式的处理和优化

在SNAM表示方法中，首先对正方形进行逆布局，然后将剩余的线段和孤立点全部归结为残渣模式，未对残渣模式进行二次优化处理，因此形成的子模式数量较多。本文将SNAM表示方法中的残渣模式，即线段和孤立点重新进行逆布局，形成新的等腰直角三角形子模式。

如图所示，图1(a)表示的是一幅未经过处理的二值图像，尺寸为2n×2n(n=3)，图1(b)表示的是一幅传统的线性四元树LQT算法对图1(a)处理后的表示结果图，形成的目标子块总数为27个，图1(c)是SNAM图像表示方法对图1(a)二值图像的逆布局结果，逆布局形成的子模式数量为12个，图1(d)改进的ISNAM图像表示方法对图1(a)二值图像的逆布局结果，形成的子模式数量为10个，显然ISNAM表示方法的子模式数量少于LQT和SNAM表示方法。

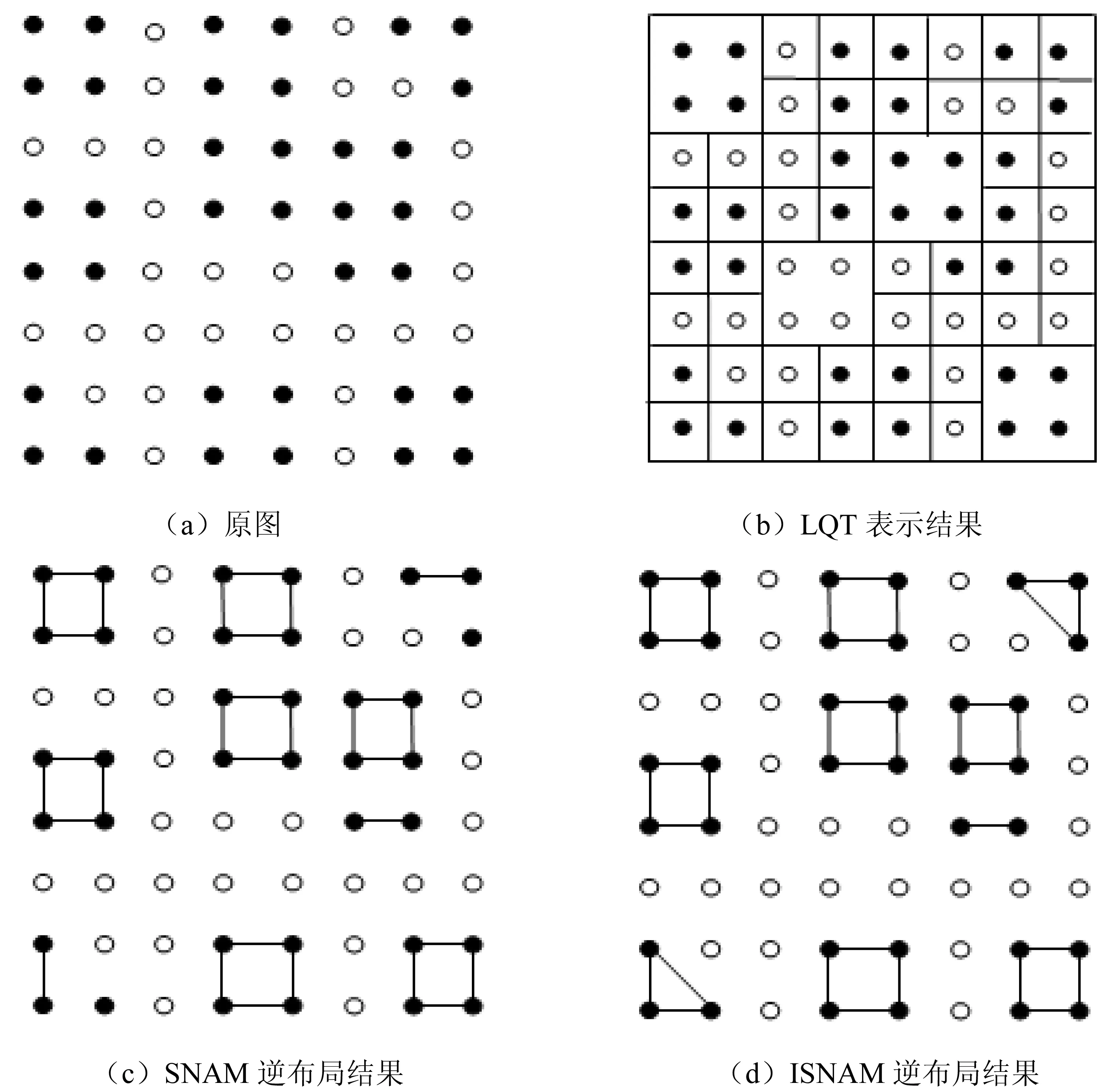
图1 原始图像及其用不同表示方法的编码结果

1.1.2等腰直角三角形子模式的设计

在算法的设计中，首先对正方形子模式进行逆布局，对残渣模式的逆布局是在最后进行，因此形成的等腰直角三角形的腰长均为1，同时根据等腰直角三角形直角顶点的位置，将其子模式分为4类，即左上、左下、右上、右下，如图2所示。

图2 等腰直角三角形的类型

1.1.3存储结构的优化

SNAM表示方法对逆布局的每一个正方形子模式和残渣模式进行了单独存储，在存储时不仅需要记录每个正方形的左上顶点坐标及边长，而且还需记录每条线段的两个端点坐标和孤立点的坐标，存储结构设计简单，因此占用了较大的存储空间。本文将边长相同的正方形子模式存储到指定的队列，实现了分类存储，因此在存储时只需记录正方形的左上顶点坐标即可，同时将类型相同的等腰直角三角形，也进行了分类存储，存储时只需记录等腰直角三角形子模式的直角顶点坐标。改进的ISNAM表示方法在逆布局后仍然存在线段和孤立点子模式，对孤立点子模式的存储同SNAM表示方法一样，但对线段的存储结构的设计优化为将长度相同的线段存储到指定的队列，因此只需记录线段子模式的第一个端点坐标即可。

对于一幅2n×2n(n=3)的二值图像，传统的线性四元树LQT表示方法存储一个黑色节点块占3(n-1)+2位的存储空间[2]，图1(b)中目标子块总数为27个，故原始图像的LQT表示将占用27×(3(n-1)+2)=27×8=216位的存储空间。根据文献[6]分析，存储一个正方形子模式需要1.5n位的空间，存储一个线段子模式需要2n位的空间，存储一个孤立点子模式需要n位的空间，图1(a)的SNAM表示方法中，存在7个正方形，3条线段，两个孤立点，因此需占用存储空间7×1.5n+3×2n+2×n=55.5位。而对存储结构优化改进后的ISNAM表示方法，存在7个正方形，两个不同类型的等腰直角三角形，一条线段，根据下文分析，存储一个正方形子模式需要n位的空间，存储一个等腰直角三角形子模式需要n位的空间，存储一个线段子模式需要n位的空间，存储一个孤立点子模式需要n位的空间，因此图1(b)的ISNAM表示方法，需占用存储空间7×n+2×n+n=30位的存储空间，因此ISNAM表示方法有效减少了图像的存储空间。

1.2算法的描述

在该方法中，预先定义边长任意的正方形子模式，但在等腰直角三角形子模式的构成中，由于直角顶点位置的不同，所以定义为左上、左下、右下、右上四种类型。因此子模式的抽象描述为正方形s={square|square=(sp,side)}、等腰直角三角形t={triangle|triangle=(type,tp)}，其中sp和side分别代表正方形左上角起始点的坐标和边长，type代表等腰直角三角形子模式类型的标示符，tp代表等腰直角三角形的直角端点的坐标，由于等腰直角三角形的四种类型腰长均相同，所以不需要存储。同时在逆布局图像时仍然会产生线段和孤立点，具体实现时也必须将它们纳入考虑，不能将其当成残渣模式丢弃，线段的抽象描述为l={segment|segment=(lp,side)}，孤立点的抽象描述为p={point|point=(p)}。以下是ISNAM图像表示算法的编码过程：

Input:二值图像T，大小为2n×2n。

Output:正方形子模式队列集合V_si、等腰直角三角形子模式集合V_ti、线段子模式集合V_li和孤立点子模式集合V_p，可以抽象描述为V={V_s,V_t,V_l,V_p}。

Step 1.采用正方形的逆布局算法，以形成面积最大的正方形为目标，按照光栅扫描的方式[7]，搜索二值图像T中未作标记的点，提取出正方形后，在T中将该正方形覆盖的像素点全部标记。

Step 2.记录该正方形子模式的边长和左上角的顶点坐标，将其二维坐标(x,y)通过降维变换为一维坐标sp，根据正方形的边长，将sp存储到指定的正方形子模式的集合V_si中，其中i为边长。

Step 3.继续循环执行Step 1到Step 2提取新的正方形，当无法提取正方形时转到Step 4。

Step 4.采用等腰直角三角形的逆布局算法，以形成等腰直角三角形为目标，搜索二值图像T中未作标记的点，提取腰长为1的等腰直角三角形，然后在T中将该等腰直角三角形覆盖的像素点全部标记。

Step 5.记录该等腰直角三角形子模式的类型和直角顶点坐标，并将其二维坐标(x,y)通过降维变换为一维坐标tp，根据三角形子模式的类型，将tp存储指定的等腰直角三角形子模式的集合V_ti中，其中i为等腰直角三角形的类型。

Step 6.继续循环执行Step 4到Step 5提取新的等腰直角三角形，当无法提取等腰直角三角形时转到Step 7。

Step 7.以形成最长线段形为目标，按照光栅扫描的方式，搜索二值图像T中未作标记的点，提取线段子模式，然后在T中将该线段覆盖的像素点全部标记。

Step 8.记录该线段子模式的左顶点坐标和长度，将其二维坐标(x,y)降维变换成一维坐标p，根据线段的长度，将p存储到指定的线段子模式的集合V_li中，其中i为线段长度。

Step 9.继续循环执行Step 7到Step 7提取新的线段，当无法提取线段时转到Step 10。

Step 10.记录在T中剩余的未做标记的点坐标，即孤立点坐标(x,y)，并将其进行降维变换为ip，最后将ip存储到孤立点子模式的集合V_p中。

Step 11.输出T的逆布局编码队列集合V={V_si,V_ti,V_li,V_p}。

2算法的理论分析

2.1存储结构分析

对于一个2n×2n的图像子模式来说，本文将正方形子模式根据边长的长度进行了分类存储，即将相同边长的正方形存储到一个队列中，同时以正方形的边长长度命名队列，因此对相同边长的正方形来说，只需存储其左上角顶点的坐标即可。在坐标存储中，一般用K码的相对值记录，因此按照K码的定义，顶点坐标的长度理论值为n位[3]，因此，存储一个正方形需要n位。

对于等腰直角三角形子模式，同样根据其直角顶点坐标位置进行分类存储，即将相同类型的等腰直角三角形存储到一个队列中，该队列以其等腰直角三角形的类型命名，由于等腰直角三角形的腰长均相同，所以腰长不需要存储，只需存储其直角顶点坐标即可，因此按照K码的定义，顶点坐标的长度理论值为n位。因此，存储一个等腰直角三角形需要n位。

对于剩余的线段和孤立点子模式而言，线段根据长度同样进行分类存储，即将相同长度的线段存储到一个队列中，该队列以线段长度命名，所以只需记录其左边顶点坐标即可，因此存储一个线段需要n位，存储一个孤立点需要n位。

2.2数据量分析

对于给定的一幅大小为2n×2n的二值图像来说，采用改进的正方形ISNAM图像表示方法编码，假设编码后产生的正方形子模式数量是NS，等腰直角三角形子模式数量是NT，线段数量是NL，孤立点数量是NP，总的数据量是HIS，根据前面章节的分析，存储正方形子模式需要n位、等腰直角三角形子模式需要n位、线段子模式需要n位、孤立点子模式需要n位的存储空间。因此总的数据量为：

HIS=nNS+nNT+nNL+nNP

(1)

若使用线性四元树编码，记录一个节点需3(n-1)+2位的空间[2]，设编码后四元树中目标(黑色)节点数量是NLQT，总的数据量是HLQT，故有：

HLQT=(3n-1)NLQT

(2)

设φLQT IS为LQT的总数据量与STNAM的总数据量的比值，则有：

(3)

由于线性四元树是对称性分割，而NAM图像表示方法是非对称性分割，所以LQT表示的节点数一般大于ISNAM逆布局算法，即NLQT>Ns+Nt+Nl+Np，所以φLQT IS>(3n-1)/n，比如当n=8时，φLQT IS>2.875>1，也就是说，LQT和ISNAM图像表示在总数据量的比值上达到了2.875倍以上。

3算法的实验分析

本节从实验的角度分析了改进的正方形ISNAM图像表示算法的相应数据，选取了4副大小为28×28的二值图像，如图3所示，该图像是图像处理中常用的图像，且与文献[6]中所用的图像一致。

图3 实验测试图像

实验具体数据如下页表1所示，其中Image表示图像的名称，C表示图像的复杂度，N表示图像的节点数或子模式数，φLQT IS表示线性四元树与正方形NAM总数据量之比，φLQT IS表示线性四元树与改进的正方形NAM总数据量之比。

表1 LQT、SNAM和ISNAM算法的性能比较

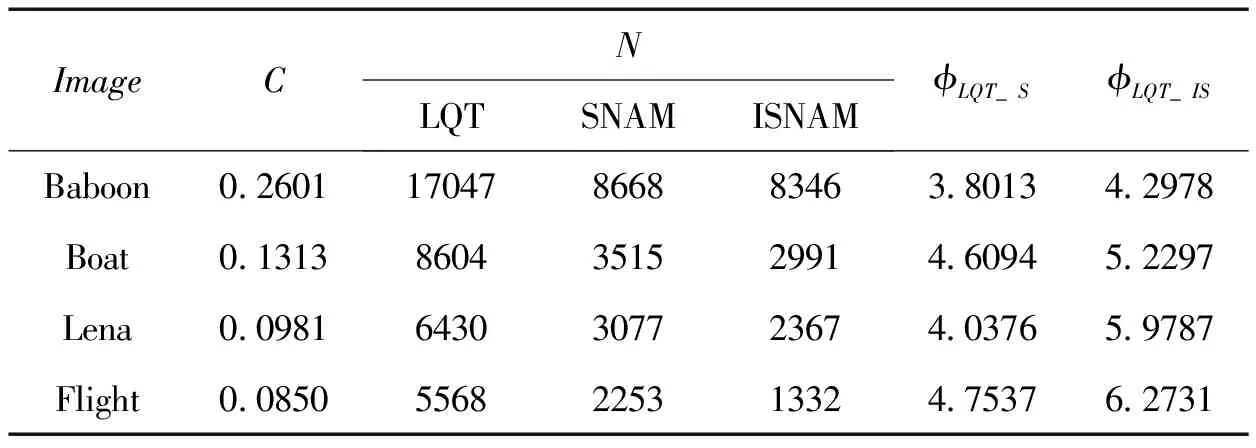
ImageCNLQTSNAMISNAMϕLQT＿SϕLQT＿ISBaboon0260117047866883463801342978Boat013138604351529914609452297Lena009816430307723674037659787Flight008505568225313324753762731

从实验数据分析来看，当图像复杂度提高时，三种图像表示方法的子模块(节点)数均有所提高，但改进的正方形NAM图像表示方法在子模式数量上均少于LQT和SNAM表示方法。当图像复杂度降低时，ISNAM表示方法的子模式数量相比较LQT和ISNAM表示方法明显减少。同时，从总数据量的比值来看，改进的正方形NAM图像表示方法也优于LQT和SNAM表示方法。

综上所述，对二值图像模式而言，无论是从理论分析，还是实验结果比较，在子模式数量的减少和存储空间的节约方面而言，改进的ISNAM图像表示方法与基于单模式的SNAM及LQT表示方法相比，均占有一定的优势。很显然，ISNAM是一种性能优良的二值图像表示方法。

4结论

本文以SNAM图像表示方法为基础，提出了改进的正方形ISNAM图像表示方法，该方法将SNAM剩余的残渣模式重新构成新的等腰直角三角形子模式。在子模式的存储方面，根据正方形的边长，等腰直角三角形的类型和线段的边长对子模式分类存储。理论和实验分析表明：改进的正方形ISNAM图像表示方法具有更少的子模式数，有效地减少了图像的存储空间，是一种值得推广的图像表示方法。

[1]M.N.Do,M.Vetterli.The eontourlet transform:an effieient direetional multiresolution image represeniation.[J].IEEE Transactions on Image Proeessing,2005,14(12):2091-2106.

[2] W.Wong,F.Y.Shih,T.Su.Thinning algorithtns based on quadtree and oetree represeniations.[J].Information Seiences,2006,176(9):1379-1394.

[3] 陈传波.非对称逆布局模式表示方法研究[D].武汉:华中科技大学,2006.

[4] 郑运平,陈传波.三角形和矩形NAM的二值图像表示方法[J].小型微型计算机系统,2009,30(8):1680-1684.

[5] 郑运平,陈传波,黄巍.一种新的基于TNAM的二值图像表示方法[J].计算机科学,2008,35(11):220-224.

[6] 贺杰,张显全,郭慧.一种基于正方形NAM的二值图像表示方法[J].制造业自动化,2011,33(3):213-220.

[7] 郑运平,陈传波.基于光栅扫描的NAM优化策略[J].华中科技大学学报：自然科学版，2008,36(8):1-4.

(责任编辑：覃华巧)

Representation Method for Binary Image UsingImproved NAM with Square

Gong Haixiao1, He Jie2, Guo Hui3

(1.2.3. College of Information and Electronic Engineering, Wuzhou University, Wuzhou 543002, China)

A representation method for binary image using improved NAM with square, which is based on the concept of non-symmetry anti-packing theory, is proposed in this paper. With the help of this method, a theoretical analysis has been conducted on its storage structure and data amount. Besides, some general binary images have been selected so as to test the method. The results show that, compared with the image representation method using NAM with square or linear quadtree, the method can decrease the image storage space effectively as well as reduce the data amount of subpatterns.

NAM; Square; Linear quadtree; Subpattern

2016-03-25

广西自然科学基金项目(2013GXNSFBA019275，2013GXNSFBA019276)

TP391

A

1673-8535(2016)03-0001-06

宫海晓(1982-)，男，山西昔阳人，梧州学院信息与电子工程学院讲师，研究方向：数字图像表示、模式识别。

贺杰(1982-)，男，湖南益阳人，梧州学院信息与电子工程学院教研室主任，副教授，研究方向：模式识别、数字图像处理。

郭慧(1981-)，女，广西梧州人，梧州学院信息与电子工程学院副院长，副教授，研究方向：图像压缩、模式识别。