谈解析几何数学实验课的教学设计

石向东

(梧州学院 信息与电子工程学院，广西 梧州 543002)



谈解析几何数学实验课的教学设计

石向东

(梧州学院 信息与电子工程学院，广西 梧州 543002)

基于知识性、实践性、操作性和计算机为一体的数学实验教学是一种有利于提高学生创新能力和综合素质的新的数学课程。文章根据解析几何学科特点，提出数学实验课教学设计的原则和课程设置方法。

解析几何；数学实验；教学设计；数学软件

1引言

随着现代社会由工业社会向信息社会过渡，国家教育部对高校培养目标及人才培养模式提出了新的要求，在高校中培养有创新能力的高素质人才已成为高等教育改革的核心问题，如何对现有教学进行改革以适应社会对人才的需求而成为高等教育的一项迫切而重要的任务。教育部在《进一步深化本科教学改革、全面提高教学质量的若干意见》中明确指出：“要坚持知识、能力和素质协调发展，继续深化教学内容和教学方法等方面的改革，实现从注重知识传授向更加重视能力和素质培养的转变”，要“着力培养学生创新精神和创新能力。”解析几何在大学数学中有着重要的地位和作用，它是理工科各专业的基础课，又是培养学生数学思维的极好教材，在当前教学改革的浪潮中，解析几何教学应朝着实现提高学生数学素养、培养创新能力的方向转变。

2解析几何课堂教学的特点

传统的解析几何课堂教学有着比较成熟的教学设计与模式，教学上注重理论的系统性和完整性，以严密的演绎思维、逻辑推理为研究方式，充分提高了学生的思维水平，体现了解析几何的理论价值。不可否认，课堂教学模式为国家培养了大批优秀人才，这是它的精华之处。

但是，传统的课堂教学忽视了对学生主动思考、自主创新能力的培养。其不足之处有如下3点。

2.1重传授，轻探索

课堂教学的方法主要是讲授法，在教学过程中，教师有条不紊、富有启发性地逐层深入讲解，加以布局合理的板书，把解析几何课程中的定理证明、公式推导、曲线与曲面的一般理论，通过演示、推理、说明和计算，使学生紧跟老师的思路，学到了系统而完整的解析几何理论知识。

在这种“传授”理念下的课堂教学，教师往往是站在知识系统化的角度去展开教学，一开始就将问题引向概念，进而提出概念的抽象表述与符号化表示方式，然后再灌输一大堆解题技巧。学生则被动地接受这些抽象的教学理论，并机械地记住有关解题方法以应付考试。这种以教师注入式的讲解代替学生思维活动的教学方式，只会导致学生不会独立思考，更不会主动探索地学习。与被动地接受教师传授的学习方式相比，主动探究的学习方式在培养学生实践能力、创新能力方面更具有深远意义。自主探究的学习方式将学生置于一种主动探索并注重解决问题的学习状态中，通过自己动手、动脑、实验等活动来了解知识的形成和发展过程。建构主义学习理论认为学生是学习活动的主体，是自己认知结构建构的决定者[1]。学生学习的主动性能否得到充分发挥，直接影响到知识建构活动的质量与效率。

2.2重演绎，轻归纳

数学的特征之一是逻辑严密性，如严谨的欧几里得几何，从几个公理出发，以演绎推理方式引出了一系列的命题，构成了一个公理化的几何论证体系，进而表现这个理论所揭示的真理，所以说数学是演绎的科学。但演绎性仅是数学的一个侧面，它的另一个侧面是归纳性。归纳推理方法由个别推及一般，由已知推及未知，所以它具有探索和发现新的数学问题和数学理论的功能。如同其他自然科学一样，数学的起源也依赖于归纳推理，因此从数学发展过程而言，数学是归纳的科学。

在解析几何教学中，要全面提高学生的数学素养，就必须既教演绎推理，又教归纳推理，但传统的课堂教学，只重视演绎思维训练，却忽视归纳思维的培养。

解析几何教材提供的是数学知识的逻辑系统，它所表现的定理证明过程是经过逻辑加工的演绎体系，同时教师也是通过“定义—定理—推论”这条演绎推理模式把“结果”传授给学生，这种演绎思维的顺序恰与数学家们在发现这些“结果”的研究活动中的归纳思维顺序相反，在这里看不到数学家创造性活动中的猜想、联想、类比、归纳等合情推理过程。

2.3重理论，轻实践

以单纯教学系统的、完整的解析几何理论为主，忽视对学生的实践能力的培养，是解析几何传统的课堂教学的又一个特点。实践是培养人的能力和智慧的摇篮，这是与学习书本知识不同的另一种学习方式，学习者在实践中体验，在实践中获得能力。随着高科技的迅速发展，数学思想已渗入到其他科学领域以及各个行业。社会对数学的需求，体现在既需要掌握数学理论的数学工作者，更需要善于运用数学知识及数学思维去解决实际问题、取得社会效益、有实践能力的人。

3在解析几何中开设数学实验课的必要性

解析几何的教学目标是培养学生的逻辑思维、空间想象能力，进而培养他们的实践和创新能力，这种创新能力可以概括为善于应用新技术获取和处理信息的能力、主动探究能力、分析和解决问题的能力。要培养这些能力，仅靠传统的课堂教学模式和原有的学习方式是难以胜任的。课堂教学只注重培养学生严密的逻辑推理能力，只注重传统系统的数学理论知识的传授，而忽视实践能力和创新能力的培养，这与国家对理工科大学生的高素质要求相差甚远。

数学实验室是一种开放式的、在数学思维活动参与下的、在特定的实验环境中进行的教学方式。数学软件强大的计算功能和图形可视化功能为学生提供了一个图文并茂、直观生动的教学环境[2]。一方面，它使一些在课堂教学中难以表达的抽象理论或无法观察到的现象如动点轨迹的形成、空间曲线的生成、曲面性质以直观形象或动画演示的方式展示出来，有效地突破了解析几何课堂教学中的难点，帮助学生深层次地理解数学理论。另一方面，学生在实验环境中动手做实验，学会猜想，学会探索，培养了创新思维能力。因此，数学实验课是课堂理论教学的有益补充，在解析几何教学中开设数学实验，是适应国家对人才的综合素质要求所作的改革举措。

4数学实验课程的设计原则

4.1实验内容取自解析几何教材的原则

根据开设数学实验的宗旨，我们认为数学实验教学内容主要是围绕解析几何的基础理论。数学实验课程的载体是“问题”，从“问题”出发，以解决“问题”为线索组成实验课的课程内容，这些内容都出自解析几何教材中，可以是一些概念、定理，也可以是空间曲线、曲面性质等。数学实验除了验证一些基本结论外，对于注重创造性思维培养的探索性实验，应有意识地去选择一些能让学生自己动手的计算机实验，并通过归纳推理等思维活动去发现结论的解析几何基本知识。

4.2数学实验与解析几何课堂教学进度同步开设原则

数学实验课与理论课一起开设，并保持相适应的进度，并且安排的课时必须适量。在不影响解析几何理论教学的前提下，我们认为开展4个课时的实验教学课较适中。围绕解析几何理论的教学内容以插入形式开设。经参考其他院校的数学实验教学大纲，我们对数学实验课程的安排大致为：第一次实验课安排在第二章轨迹与方程；第二、第三次安排在第四章，目的使学生在数学实验中用实验方法去探究曲线或曲面性质；第四次则安排在第五章进行。

4.3操作性与探索行相结合原则

数学实验课是一门强调实践与探索的课，具有很强的操作性,学生通过数学实验，自主探究，合作交流，也就通过“做”数学去探究数学规律。这是一个动手与动脑相结构性合的过程，因此要把握“做”的度，不能只顾操作性而忽视数学思维探索性的培养，要求学生既能运用计算机得到相应的数据，又能对数据进行数学分析并得出结论[3]。

4.4实验课题的选择与教学目标相匹配原则

作为解析几何课程的数学实验，其着眼点除了通过自主探索与实践达到培育创新能力外，还应通过数学实验掌握解析几何相关概念与定理，如围绕曲面截痕轨迹的形成使学生学习曲面的形状与性质，围绕维维安尼曲线的画法掌握空间曲线的射影柱面的来龙去脉与性质等等。

5解析几何数学实验课的教学设计

国内开设数学实验课主要有两种形式，一种是独立开课，即指独立于大学数学各基本课程之外，单独开设数学实验课程，另一种是在各基础课程的教学中引入数学实验课，把它作为各数学基础课程的教学环节[4]，根据学校的具体情况和解析几何教学改革的现状，我们采用后一种形式。

与把数学实验作为一门独立的课程来开设不同，作为引入解析几何课的数学实验，定位为让数学实验与解析几何课堂教学优势互补，掌握解析几何的基本理论和学习方式培养他们的探索精神和创新能力，因此数学实验的内容都取自解析几何教材，包括某些概念、定理、公式等。按教学方式、教学目的以及思维训练水平来分，我们将实验分为两种：一种是验证实验，用计算机验证一些已学的结论或公式；另一种是探索实验，强调探索一些复杂的解析几何定律或公式。前者着眼于“结果”的验证，后者着眼于“结果”的发现[5]。

5.1验证性实验

解析几何课堂教学已把数学理论传授给学生，如概念、定理等，但学生往往对这些知识的理解是抽象的、片面的、生疏的。在数学实验课上，通过学生自己动手以实验检验这些已知的结论的正确性，帮助学生更好地理解和掌握解析几何的基本理论。许多空间曲线和曲面的形成，是无法由教师在课堂上用静态的示图和口头语言讲清的，计算机“可视化”的动态演示，把曲线或曲面的形成过程准确地模拟出来，对提高学生的空间观念、数形结合思想水平和教学效果起到事半功倍的作用。

案例1：演示动点或动直线的轨迹的生成。

动点或动直线的轨迹是解析几何又一难点。利用matlab的图形可视化功能，可以把轨迹的形成过程准确地模拟出来，对提高学生的空间观念有很好的效果。

例：有两条相交的直线l1与l2，其中l1绕l2作螺旋运动，即l1一方面绕l2作等速转动，另一方面又沿着作等速直线运动，在运动中永远保持与l2直交，这样由l1所画出的曲面叫螺旋面。

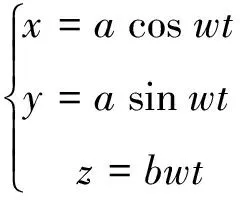
通过对问题的变形以及利用数学软件制作动画准确地模拟轨迹的生成过程，使学生对动点的轨迹是曲线，动直线的轨迹是曲面有了深刻的认识。

案例2：认识空间曲线关于坐标平面的射影柱面，射影柱面在认识空间曲线方面的作用、有利于空间曲线的作用。

例：画出维维安尼曲线。

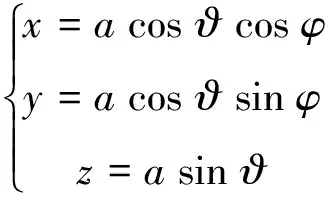
验证性实验的特点是直观、动态，使深奥的解析几何理论以图形、动画等形式动态地出现，达到简单明了、直观易懂、化难为易的教学效果。

5.2探索性实验

数学上的概念、定理、公式的产生都是科学家们创造性思维的“结果”，是一个归纳→猜想的归纳思维过程,但教材却表现为概念→定理或公式→范例组成的数学系统,是一个逻辑严密的演绎体系,教材掩盖了这些“结果”的探索、发现、形成的复杂过程，只把思维的“结果”显示出来。同时，传统的教学方式也普遍地存在重结论、轻过程的现象，这种把结论、过程直接展示给学生的教学方式，使学生只记住了定理与公式，却没有思维活动的空间，更谈不上质疑。探索实验型教学模式打破了教材中以逻辑形式展示知识的演绎体系，从归纳的方法去学习它，就是归纳→猜想→证明的学习模式。在归纳环节中，让学生编程序，观察计算机的图形演示和实验过程，从实验结果中分析、归纳、形成猜想，发现数学规律。现代教育理论表明，发现式的学习以问题解决为中心，学生在动手、动脑的学习活动中，通过观察、分析、综合、归纳、猜想等思维操作，学会解决问题和探索真理的能力。探索实验型教学为实施发现法学习提供了很好的平台。

在这种模式里，学生不知道“结论”的。首先教师在解析几何教材中选择一些概念、定理、或典型的问题设计成问题，使它与重要的知识和原理等结合在一起，从而使学生在利用数学实验解决这类问题时，能利用到与这个问题相联系的知识或原理去解决它。然后由学生在计算机上设计和实验，并在这个过程中不断尝试、修改、完善实验结果，并对实验结果进行分析、猜想，最后得出“结论”，达到解决问题的目的。

案例3：用截痕曲线研究曲面形状与性质。

柱面和锥面以它们各自的生成方式来给出定义，从定义中就可知道柱面或锥面的性质及形状，并很容易用图形来表示。与柱面和锥面的定义方式不同，椭球面、双曲面和抛物面是用方程来定义的，也就是解析定义。解析定义没有明显的几何特征，为了研究它们的形状与性质，必须用平行截割法，即用一组平行平面去截割这种用方程表示的曲面，得到一族截痕曲线，通过研究这些截痕曲线的变化趋势去推想曲面的几何性质和整体形状，这种推想方法抽象程度较高，学生感到难以掌握。笔者指导学生利用数学软件(如Matlab)，在数学实验课上自主探索曲面的形状与性质。程序为：

(1)实验演示

学生利用Matlab制作动画，方法是将截痕曲线设置为逐个出现，学生容易看出曲面截痕轨迹的形成过程。

(2)分析与归纳

学生根据以平行于平面的一组平行平面所截得的一系列截痕曲线，分析这些截痕曲线的形状变化趋势以及它们的端点运动情况。

(3)推想与总结

案例4：演示旋转曲面的形成过程，研究曲面性质。

在计算机上制作旋转抛物面x2+y2=2pz的动画演示，虽然数学软件上没有动画命令，教师可引导学生制作抛物线的图形序列。该旋转抛物面是由yoz平面上的抛物线y=2pz绕对称轴(z轴)旋转而成，这种旋转过程可以由平面曲线y2=2pz逐个出现，显示形成动画，直观形象地演示了抛物线绕旋转轴z轴旋转而成旋转抛物面的过程，生动地揭示了旋转抛物面的本质。学生在实验演示之后，总结出曲面性质。

从以上案例看到，数学实验课程通过计算机图形显示、动画模拟，形成一个形象生动的教学环境，给解析几何教学带来了先进的教学手段，打破了以教师为中心的满堂灌，使教学成为“以学生为中心，教师为主导”的师生互动模式，并使学生在数学实验中学会“提出问题、发现规律、提出猜想、进行证明”的探索与创新能力。因此数学实验对解析几何传统教学方式是一种有益的补充。探讨数学实验与传统教学如何达到优势互补，仍是我们今后要作的进一步研究。

[1]黄文.用建构主义理论指导创造性思维方式的培养[J].广西高教研究，1999(2).

[2]韩明，王家宝，李林.数学实验[M].上海：同济大学出版社，2009.

[3]许立炜.数学实验课程中的实验设计原则[J].大学数学，2010(8).

[4]陈晓瑛，龚日超.国内外数学实验教学的现状分析与展望[J].株洲师范高等专科学校学报，2004(10).

[5]李继成，朱旭，王绵森，等.数学实验课程建设及分层次教学与实践[J].大学数学，2005(12).

(责任编辑：高 坚)

On Teaching Design for Mathematical ExperimentalCourse on Analytic Geometry

Shi Xiangdong

(College of Information and Electronic Engineering, Wuzhou University, Wuzhou 543002, China)

Mathematical experimental teaching and learning based on the natures of knowledge, practice and operation and integrated with computer systems is a new mathematical course which is helpful for the improvement of students’ innovation ability and comprehensive quality. Based on the characteristics of analytic geometry, this paper puts forward some principles for teaching design of mathematical experimental course and some approaches to course arrangement.

Analytic geometry; Mathematical experiment; Teaching design; Mathematical software

2016-04-01

梧州学院教学改革项目(Wyjg2014B011)

G642.4

A

1673-8535(2016)03-0063-06

石向东(1961-)，男，广西梧州人，梧州学院副教授，主要研究方向：微分方程。