一种改进的多尺度Harris算法
2016-12-20杨秋慧
杨秋慧
(梧州学院 广西高校图像处理与智能信息系统重点实验室,广西 梧州 543002)
一种改进的多尺度Harris算法
杨秋慧
(梧州学院 广西高校图像处理与智能信息系统重点实验室,广西 梧州 543002)
传统Harris算法依据经验确定兴趣值计算参数,并且对于一些类型的角点识别能力较差。针对这些问题,该文提出了一种基于局部标准差和对数计算的多尺度角点检测方法。该方法通过对数化梯度取降低边缘响应对候选点兴趣值的影响,有效地检测不同类型的角点。并重新定义兴趣值函数,由标准差的统计特性计算兴趣值,避免主观选择参数,使算法具有更高的客观性。实验结果表明,该方法具有检测复杂类型角点、精确定位,并具有旋转、灰度、噪声、尺度不变性。
角点提取;Harris 算法;标准差;定位
角点是图像灰度变化剧烈的点或图像边缘曲线的曲率极大值点。曲线或直线的交叉点,图像区域的中心点,小波变换的局部极值点等等,这些能够用某种相似性度量准则提取出来的显著点都可以作为图像的角点。这些点保留了图像的重要特征,对图像匹配,目标跟踪、运动估计等后续图像处理有重要意义。由于角点对图像几何形状的不变性和易于被观察者所接受,在特征点提取算法中可作为控制点。
角点可以定义为局部区域内灰度变化剧烈的点、目标区域边缘曲线的曲率极大值点、曲线或直线的交叉点、图像区域的中心点、或小波变换的局部极值点等等,能够用某种相似性度量准则提取出来的、包含图像的重要信息的显著点。根据对“角点”不同的定义,可将角点检测方法主要分为两类:基于边缘的方法和基于图像灰度的方法。基于边缘的方法采用提取图像边缘并编码,然后计算边缘曲率,根据曲率是否为极值判断该点是否为角点。其中,一些方法是直接对曲线进行拟合,另一些则是用某类函数对曲线进行分段拟合,然后根据这些拟合的分段方程计算曲率极值点的位置[1-2]。基于边缘的方法处理效果依赖于图像分割和边缘提取的结果,当被检测图像发生变化时,可能会导致结果错误,并且对噪声敏感、计算量大。基于邻域灰度的方法,主要根据邻域内灰度的变化情况确定角点位置,如以某种局部结构特性、灰度相似性等特征作为筛选角点的条件。Harris角点检测方法[3-5]、KLT[6],MIC[7-8],SIFT[9-11]算法等都是基于领域灰度的方法。其中,SIFT算法在尺度空间中寻找极值点,对于存在部分遮挡、拍摄角度变化等情况较好的稳定性。该算法信息量丰富,但是过程较复杂,包含大量的浮点数运算,而且提取的特征点没有直观地反映图像的结构特征。近年来,国内外研究者对这些经典算法进行了多种改进[12-16]。
本文通过对传统Harris算法进行分析,通过选取边缘附近的像素点作为候选点,减少计算量。对候选点筛选时,对梯度值取对数值,降低位于角点附近的边缘点的边缘响应对角点兴趣值的影响,更有效地检测出复杂类型的角点。最后,为提高角点的定位精度及尺度不变性,采用非极大值抑制和多尺度的Harris算法检测角点,并使用标准差重新定义了角点的兴趣值函数。
1Harris算法
Harris算法是由ChrisHarris在1988年提出的,它是在Moravec角点提取算法的基础上,采用边界曲率描述灰度变化的情况。Harris角点提取算法,计算简单,只用到一阶差分及滤波计算,提取的角点均匀分布在图像上。算法需要对图像中的每个点都计算兴趣值,然后选择最优角点位置。该算法有很好的稳定性,对图像旋转、灰度、噪声等变化鲁棒性较好,但不具有尺度不变性。下面简单介绍该算法的主要步骤。

(1)
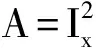
(2)
其中,W为高斯平滑函数。
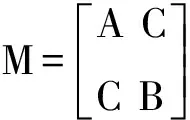
(3)
M矩阵为二阶实对称阵,故存在两个特征值λ1,λ2。这两个特征值反映像素点的特征,因此能够根据特征值来判别像素点是位于平滑区、边缘还是角点。λ1,λ2的取值有以下3种情况:
(1)λ1,λ2为正值并且都较大时,M矩阵为峰值,各个方向相邻像素点之间灰度差值都较大,则认为这个像点为角点;
(2)当其中一个特征值较大,一个特征值较小时,M为山脊形,沿着山脊方向的相邻像素点灰度变化很小,而垂直山脊方向的变化很大,那么该像素位于图像边缘上;
(3)当λ1,λ2都较小时,M矩阵是平滑的,该像素位于图像平滑区。
于是,由M矩阵的行列式和迹计算Harris角点的兴趣值,见公式(4)和公式(5)。
Det(M)=αβ=(AB)-C2Tr(M)=α+β=A+B
(4)
C(x,y)=Det(M)-k×Tr2(M)=(AB-C2)-k(A+B)2
(5)
其中,k为经验值,取值区间为0.04~0.07。局部范围内的极大兴趣值点就被认为是角点。由于极值点的数量往往较大,因而需要较大的计算量。
Harris角点检测方法对T,Y,X形的角点检测效果较差。图像中若含有大量结构复杂的角点,Harris算法检测结果会漏掉这些类型的角点,导致后续的图像分析精确度下降。
2改进的算法
本文通过对Harris算法的研究和分析,对传统算法进行相应的改进。改进的算法流程如图1所示。
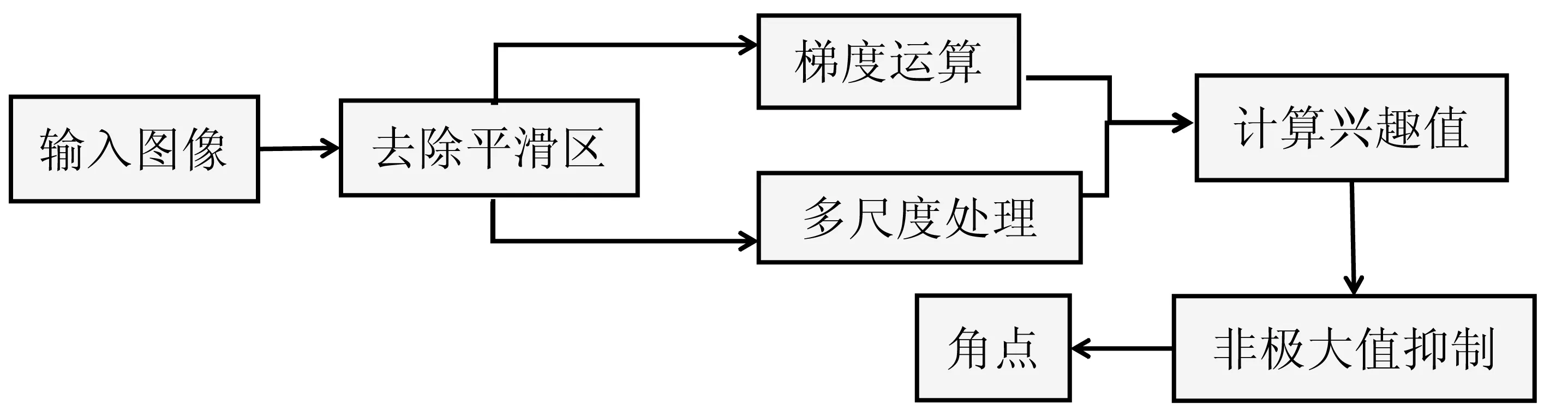
图1 改进的算法流程图
角点是位于边缘附近的,因此本文先对图像进行筛选,去除平滑区域,将边缘附近的点作为候选点,以减少计算量。然后,算法准确地区分角点和边缘点,达到提取角点的目的。
当候选点位于角点附近时,由于窗口W中包含大量边缘点,这些点的特征值α≫β,得到的兴趣值与角点的兴趣值均较大,混淆了算法对于角点的判断。本文对此进行改进,通过对数化候选点的梯度值,抑制边缘附近的候选点特征值中较大的值,降低边缘响应对计算兴趣值的影响,从而达到提高角点定位精度的目的。则有公式(6)、公式(7)、公式(8)。
(6)
log(G′(x,y))=log(G(x,y))
(7)
计算中仅仅改变了梯度的值,梯度的方向不变,故G’θ(x,y)=Gθ(x,y)。
根据公式(1)以及梯度的求值公式,可得:
=(G′(x,y))*cos(Gθ(x,y))
(8)
(9)
使用I’x,I’y分别来代替Harris算法公式(2)中的Ix,Iy。抑制角点附近的边缘点的兴趣值对判断角点的影响。
传统算法的兴趣值C(x,y)计算需根据经验确定参数k的值,具有主观性,降低检测的稳定性。本文用标准差的计算来取代对参数k,重新定义了兴趣值函数,自动地判别角点。为增强角点的尺度不变性,同时采用laplace多尺度算法,通过非极大值抑制法和兴趣值的大小来确定角点的位置。
I′(x,y,s,δD)=I⊗W(x,y,sδD)

(10)
其中,i=1,2,3,....,N为候选点总数目。d1,d2分别表示矩阵M’的行列式和迹平方的均值,兴趣值函数中两部分分别为行列式和迹平方的标准差。
由于角点的两个特征值都较大,而边缘附近的像素点,两个特征值中仅含一个较大值,且候选点所包含的边缘点数目远大于角点数目,因此,
(1)当R(x,y)>0时,候选点为角点。角点响应大于边缘响应。
(2)当R(x,y)<0时,候选点为边缘点。边缘响应大于角点响应。
对于每个候选点分别计算其兴趣值,结果大于零,并且是局部极大值,那么这个点被判定为角点,不需要Harris算法中筛选角点时选取阈值,可以直接区分出角点和边缘点;反之,则判断为边缘点。
3实验结果
实验是在操作系统为Windows7的微机上进行的,使用MATLAB7.10对图像进行处理。

图2 图像1

图3 图像1的细节部分
图3为图2中圈出的部分放大后的图像。从上述实验可以看出改进的算法能够更好地检测出复杂类型的角点,改进后的Harris算法能够更加准确地定位角点的位置。
对于图2中图像的角点提取效果,两种算法的比较如表1所示,改进后的算法可以提取到足够数量的角点,有较少的缺失及错误的角点数,能够更加准确地提取各种类型的角点。
表1 两种算法的效果对比

图像算法角点总数检测的角点总数错误角点数正确的角点数缺失的角点数图像1Harris改进的Harris607144614583555
实验表明,算法对于实际场景图像的角点提取也有着良好的效果,如图4所示,图中用圆圈标记检测出的角点,相对于Harris算法,可以获得数量充足、多种复杂类型的角点,并且对于旋转、灰度及噪声均具有较好的稳定性,角点的定位更接近于实际物体的角点位置。

图4 两种算法结果对比
从表2的数据可以看出,本文改进的算法在旋转、缩放、灰度变化以及噪声变换情况下,角点的复现率均比Harris算法高,能取得更好的提取效果。
表2 原图1复现率比较

原图像旋转图像缩放图像灰度反转加噪图像Harris算法特征点数26692807210926664584复现率441%442%534%683%改进的算法特征点数72562384466541复现率676%663%849%767%
4结论
本文提出一种改进的Harris角点提取算法,有效地改善了传统Harris算法对T、X、Y等类型角点无法检测出来的问题。通过数据的统计特性,定义新的兴趣值函数,消除兴趣值计算中的参数的经验取值,降低了对算法的主观性,取得比原算法更好的实验结果。本文的算法不仅对于角点的定位更加精确,还保持了算法对于旋转、灰度变化、尺度以及噪声较好的稳定性。但是,角点定位精度也仍旧只精确到像素级,维持在与图像像素相同的精度。
[1]L Kitchen, A Rosenfeld. Gray Level Corner Detection[J]. Pattern Recognition Letters, 1982, 3(1): 95-102.
[2]钟宝江,廖文和.基于精化曲线累加弦长的角点检测技术[J].计算机辅助设计与图形学学报,2004,16(7):939-943.
[3]Harris C G, Stephens M J. A combined Corner and Edge Detector[A]//Proceedings Fourth Alvey Vision Conference. Manchester, 1988.
[4] Misra I, Moorthi S M, Dhar D, et al. An automatic satellite image registration technique based on Harris corner detection and Random Sample Consensus (RANSAC) outlier rejection model[C]//Recent Advances in Information Technology (RAIT), 2012 1st International Conference on. IEEE, 2012: 68-73..
[5]吕恒利,尚振宏.基于Harris角点和SIFT算法的车辆图像匹配[J].昆明理工大学学报:自然科学版,2015,40(1):50-54.
[6]Ramakrishnan N, Srikanthan T, Lam S K, et al. Adaptive Window Strategy for High-Speed and Robust KLT Feature Tracker[M]//Image and Video Technology. Springer International Publishing, 2015: 355-367..
[7]Fanzhi K, Xiao X. SIFT-MIC Based Matching Location Algorithm for Wire Bonding[C]//3rd International Conference on Multimedia Technology (ICMT-13). Atlantis Press, 2013:1349-1355.
[8]孙亮,王双庆.一种基于自适应阈值的改进MIC算法[J].微电子学与计算机,2015,32(5):79-83.
[9]Kang T K, Zhang H, Kim D W, et al. Enhanced SIFT descriptor based on modified discrete Gaussian-Hermitemoment[J].ETRI Journal, 2012, 34(4): 572-582.
[10]Yi J K, Bian G H, Jiang D G. Optimization of scale-invariant feature transform(SIFT) feature extraction[J]. Journal of Beijing University of Chemical Technology, 2013, 40(1): 115-119.
[11]范宗杰,徐向辉.一种基于SIFT算法的SAR图像配准方法[J].电子测量技术,2014,37(8):70-74.
[12]Xing Y, Zhang D, Zhao J, et al. Robust fast corner detector based on filled circle and outer ring mask[J].IET Image Processing, 2016, 10(4):314-324.
[13]Liao B, Xu J, Sun H, et al. Robust Corner Detection Based on Bilateral Filter in Direct Curvature Scale Space[M]//Advances in Swarm and Computational Intelligence. Springer International Publishing, 2015: 357-365.
[14] Peng W, Hongling X, Wenlin L, et al. Harris Scale Invariant Corner Detection Algorithm Based on the Significant Region[J]. International Journal of Signal Processing, Image Processing and Pattern Recognition, 2016, 9(3): 413-420.
[15] Lei Zhang, Kuiyuan Yang, Hongxun Yao. Nested-SIFT for efficient image matching and retrieval[J].MultiMedia, IEEE, 2013, 20(3):34-46.
[16]陶雪焦.改进的多尺度Harris亚像素角点检测[J].工业控制计算机,2016,29(3):50-52.
(责任编辑:覃华巧)
An Improved Harris Algorithm with Multi Scales
Yang Qiuhui
(College of Information and Electronic Engineering, Wuzhou University, Wuzhou 543002, China)
Traditional algorithms of Harris needs to decide parameter for computing interest values of pixels by experience and the recognition ability for some types of corners is poor. To solve these problems, this paper proposes a corner detection method based on local standard deviation and logarithmic computing. The method decreased the response values of corners near the candidate interested points through computing the logarithms of gradient, so it can detect corners with different types more effectively. And then, according to the statistical features of the standard deviation, it redefines the interest value function. The function could avoid subjectively selecting the value of parameters and it could directly judge whether a candidate interested point is a corner, which makes the algorithm more objective. The experimental results show that the method can effectively detect the corners with various types and it has a more accurate effect of positioning.
Corner detected; Harris algorithm; Standard deviation; Positioning
2016-03-28
国家自然基金项目(61562074);广西高校科学技术研究项目(KY2015YB290);梧州学院科研项目(2011C002)
TP391
A
167-8535(2016)03-0007-07
杨秋慧(1990-),女,河南省信阳市潢川县人,梧州学院信息与电子工程学院教师,研究方向:图像处理。
