基于最小冲击的三自由度永磁球形电机轨迹规划
2016-12-20吴凤英翟献超张登权
吴凤英,翟献超,张登权,李 睿
(天津理工大学,天津 300384)
基于最小冲击的三自由度永磁球形电机轨迹规划
吴凤英,翟献超,张登权,李 睿
(天津理工大学,天津 300384)
为了提高三自由度永磁球形电机在指定时间内完成运动任务的平滑性,减小运动过程中的振动程度,提出一种能达到最小冲击的轨迹规划方法。为保证冲击连续,该方法采用5次B样条曲线插值位置序列,将运动学约束转化为B样条曲线控制顶点约束,以冲击平方积分的最小值作为平滑性能指标。采用遗传算法对最小冲击性能指标和相对应的时间节点向量全局寻优,规划出最小冲击轨迹。最后,通过仿真实验验证了该方法的可行性和有效性。
三自由度; 永磁球形电动机; 最小冲击;B样条; 遗传算法
0 引 言
永磁球形电机是一种工作原理新颖,高度集成化的机电能量转换装置,具有机械集成度高、体积小、传动链简单、精度高、节能等优点[1]。永磁球形电机的轨迹规划是永磁球形电动机运动控制的重要内容之一,其目的是在满足运动学及动力学约束条件下,利用合适的方法规划出运动轨迹,通过指定路径点,计算其运动学参数,以满足运动平稳,轨迹平滑连续的要求。
对球形电机的运动控制,各国学者进行了一些研究,并取得了一定的科研成果。针对永磁球形步进电机,Kok-Meng Lee等人建立了三自由度耦合运动的动力学约束方程,并在此基础上实现球形电机的实时运动控制[2-5];约翰霍普金斯大学的David Stein等人利用RO3旋转群理论和势函数对运动过程进行了规划[6-7];国内的王群京等人利用四元数描述球形转子的三自由度转动,并将自适应模糊控制等策略应用于球形电动机的运动控制过程[8-11]。这些研究着眼于从原理上解决球形步进电机的轨迹规划问题。针对永磁球形直流电动机,谢菲尔德大学的Wang J等人利用永磁球形直流电动机模型结合运动学模型和动力学模型,实现了永磁球形电动机的运动控制[12-13];亚琛工业大学K. Kahlen等人采用空间转矩矢量的排序算法、分类方法和近似算法实现了电机的实时运动控制[14];南洋理工学院的Yan L等人推导了基于球谐级数的磁场力矩解析模型,并对其运动规划和控制做了初步探索[15-16];天津大学等研究机构将计算转矩法应用于永磁球形电动机动力学模型,实现了永磁球形电动机的力学解耦控制[17]。上述的研究和实验在原理上成功实现了永磁球形直流电动机连续轨迹的运动控制,但是,这些研究主要集中在运行机理、运动控制策略等单一问题的分析与解决上,没有涉及对运动过程中角速度、角加速度和冲击等状态变量的规划。在轨迹规划中,平滑、快速、低耗、冲击小等性能指标是非常重要的几个指标[22-27],本文针对三自由度永磁球形电机连续运动轨迹的规划问题进行了研究,以最小冲击为规划目标并考虑在运动过程中角速度、角加速度和冲击的运动学约束,提出一种采用五次B样条曲线插值位置序列的轨迹规划方法,提高三自由度永磁球形直流电动机在指定时间内完成运动任务的平滑性,减小运动过程中的振动。
1 永磁球形电机最小冲击轨迹规划问题描述
1.1 永磁球形电机运行原理及等效模型
永磁球形电机运行原理如图1(a)所示,它由定子线圈和球形转子组成,在壳型定子上均匀排列若干个定子线圈,在球形转子上沿赤道两侧均匀粘贴永磁体;单个定子线圈与永磁体作用产生电磁力驱动球形转子运动,多个定子线圈产生的转矩可分解为三个自由度方向上的转矩驱动球形转子实现三自由度运动。球形转子的运动姿态通常用方位矩阵表示,也可采用欧拉角或四元素法表示,考虑到欧拉角参数较少,采用欧拉角表示。在这种情况下,球形转子的运动可以等效为具有3个旋转关节的四杆结构,等效模型如图1(b)所示,此四杆机构由依次串联的杆件0、杆件1、杆件2、杆件3构成开链机构,球形转子安装在杆件3上。杆件0、杆件1、杆件2、杆件3之间由单自由度旋转运动副链接,各杆件的链接关系如图1所示。杆件1、杆件2、杆件3均可绕前一杆件作旋转运动,3个运动副轴线彼此正交于O(o)点,各杆件的质量均为0。三自由度球形电机与特定的三连杆工业机器臂具有相同结构形式的运动学模型和动力学模型。
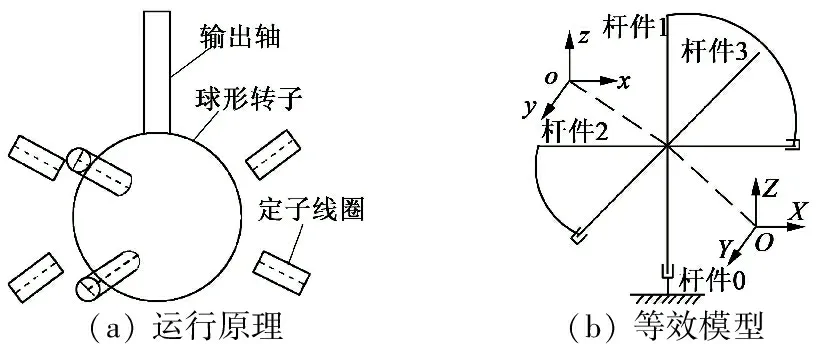
(a)运行原理(b)等效模型
图1 永磁球形电动机运行原理及等效运动模型
1.2 永磁球形电机最小冲击轨迹规划

永磁球形电机的运动过程可以用位姿余弦矩阵表示,根据球形转子的位姿余弦矩阵逆运动学反解求出角位移位置序列θmi和对应的时间ti,构成一系列的角位移-时间序列 然后采B样条曲线插值角位移-时间序列得到相应的轨迹曲线θ(t)={(θmi, ti)|i=0,1,…,n}。
等效关节的冲击累积越小,轨迹越平稳,将等效关节冲击平方积分作为优化指标,构造最小冲击轨迹规划问题的目标函数:
(1)
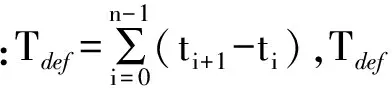
球形转子运动轨迹还必须运动学约束的要求:
(2)
式中:cvm,cam,cjm分别为关节m的速度、加速度、冲击约束。所以三自由度永磁球形电机最小冲击轨迹规划是在满足以上目标函数与约束条件综合作用下的最优轨迹寻优过程。
2 基于B样条的最小冲击轨迹规划
三自由度永磁球形电动机角位移轨迹用B样条可描述:
式中:θ(u)为时刻u处的输出轴位置,di(i=0,1,…,n)为控制顶点,u为定义k次B样条的定义域向量u=[u0,u1,…,ui+2k]。并且有:
Ni,k(u)(i=0,1,…,n)为k次B样条基函数,它是由非递减参数节点矢量u组成k次分段多项式,由德布尔-考克斯递推公式可得:
(3)
B样条曲线具有局部支承和Ck-1阶连续特性,其r阶导数可由德布尔-考克斯递推公式求出,即:
(4)
求导得:
(5)
取k=5,得到n+5个控制顶点的向量的n+5个方程。即:
(6)
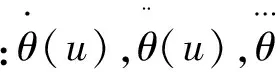
3 遗传算法寻优
3.1 运动学约束处理
三自由度永磁球形电机的轨迹规划过程是受各种因素限制的,包括位移、速度、加速度和冲击的约束。将以上运动学约束转化为B样条控制顶点的约束,由于三自由度永磁球形电机的结构特点导致输出轴的运动范围受限,也就是球形电机的运动轨迹是受限的,故存在位移约束:
其控制顶点还应满足:
(7)

结合式(1)和式(7),可将三自由度永磁球形电机规划描述为描述为以下非线性约束问题,即:
(8)
由于B样条具有强凸包性,所以只要满足以上约束条件的最优化冲击最小轨迹对应的时间节点向量和全局最小累计冲击Δt*和J(Δt*)就是全局极小点。
3.2 遗传算法寻优
将约束条件转化为遗传算法中的罚函数:

(9)
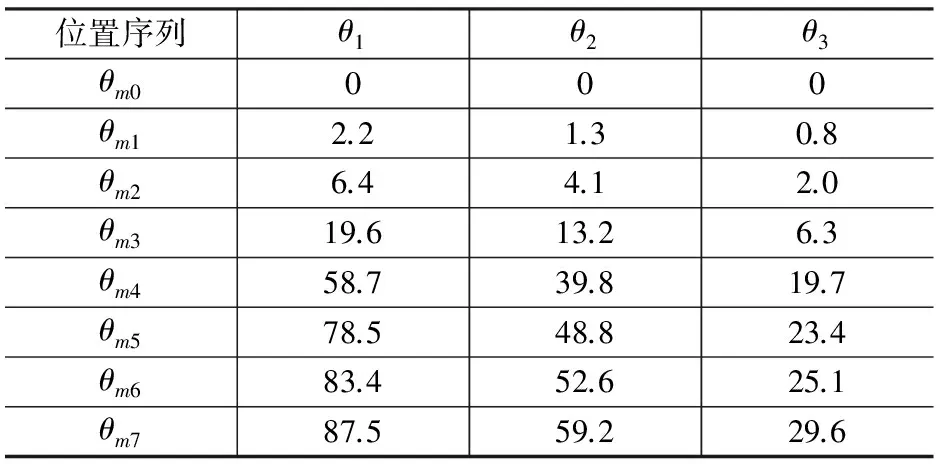
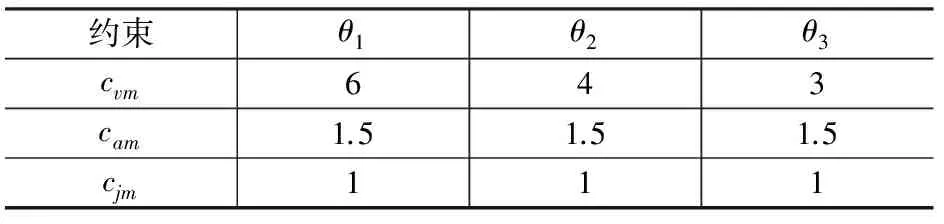
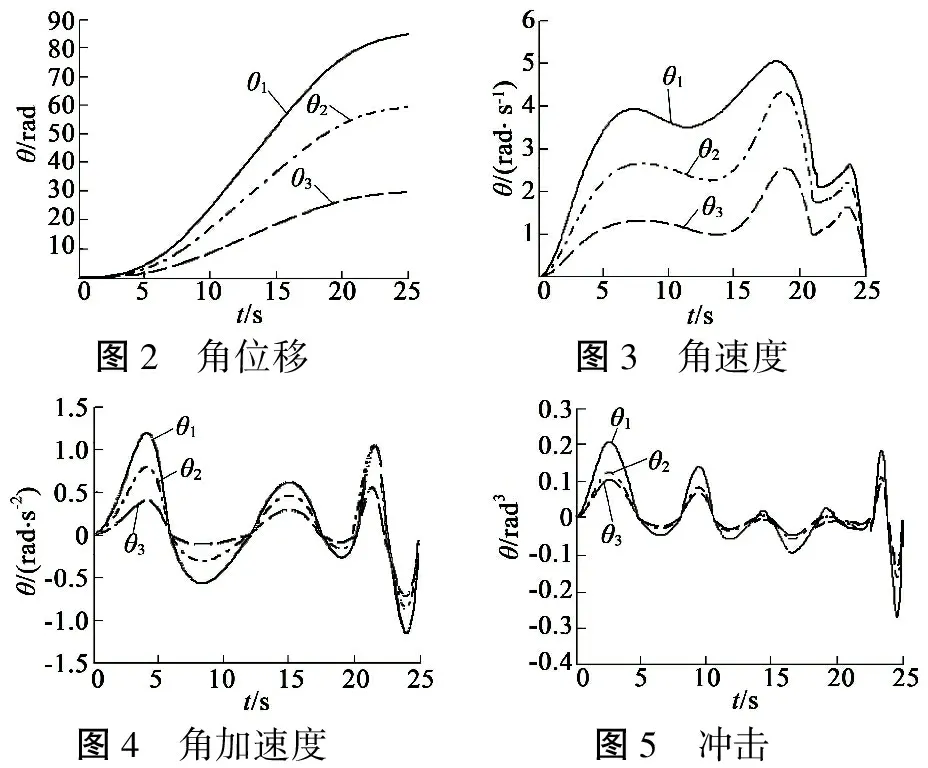
式中:μi(i=1,2,3)为待定系数,由MATLAB工具箱中的GeneticAlgorithmTool来进行遗传算法的运算,其默认为求适应度函数的最小值。选择算子和交叉算子均选用遗传算法工具箱默认的设置。变异算子采用非一致变异方式,设变异概率为ym,对群体中的每一个个体Xi随机选取其中某一变量xi,在(0,1)内产生一随机数r,若有r 通过遗传算法可求解出适应度函数最小时三自由永磁球形电机各段轨迹最优的时间间隔Δt*。将优化后的时间间隔与相应的位置序列通过B样条连接得到其冲击最小的轨迹规划曲线。 基于三自由度永磁球形电机的几何参数,在MATLAB上进行了仿真实验,结合其角位移范围约束、角速度约束、角加速度约束和冲击约束条件,验证算法的有效性。设球形转子的初始位姿R0和终点位姿Rf用方向余弦矩阵分别表示: 通过逆运动学公式反解得到位置序列如表1所示。 表1 位置序列 运动学约束如表2所示。 表2 运动学约束 设定起停速度、加速度和冲击均为0,冲击最小轨迹执行时间Tdef,采用遗传算法,得到轨迹全局最小累计冲击J(Δt*)和对应的时间节点向量Δt*。设定Tdef=25s,得到冲击最小轨迹的时间节点向量Δt*=[3.59,4.26,3.34,4.03,3.21,3.42,3.15 ]T。其轨迹规划的位移、速度、加速度和冲击的仿真结果如图2~图5所示。 图2 角位移图3 角速度图4 角加速度图5 冲击 本文提出一种基于五次B样条的三自由度永磁球形电机轨迹规划方法,并且结合角速度、角加速度和冲击限制的运动学约束进行规划,使用遗传算法对性能指标和时间节点向量寻优,得到了在限定时间内经过指定位置的冲击最小的轨迹规划方法,保证冲击的连续性和规划出的轨迹平滑性,并且本方法亦可用于三自由度永磁球形电机的避障轨迹规划。 [1] 李争,王咏涛,葛荣亮,等.永磁球形多自由度电机研究进展综述[J].微电机,2011,44(9):66-70. [2]LEEKM,VACHTSEVANOSGJ,KWANCK.Developmentofasphericalwriststeppermotor[C]//ProceedingsofIEEEInternationalConferenceonRoboticsandAutomation,1988:267-272. [3]LEEKM,KWANCK.Designconceptdevelopmentofasphericalstepperforroboticapplications[J].IEEETrans.onRobotsandAutomation,1991,7(1):175-180. [4]BAIK,LEEKM,FOONGS.Directfield-feedbackcontrolformulti-DOFsphericalactuators[C]//Proceedingsofthe2011InternationalConferenceonRoboticsandAutomation,2011:5825-5830. [5]SONH,LEEKM.Open-loopcontrollerdesignanddynamiccharacteristicsofasphericalwheelmotor[J].IEEETransactionsonIndustrialElectronics, 2010,57(10): 3475-3482. [6]CHIRIKJIANGS,STEIND.KinematicDesignandcommutationofasphericalsteppermotor[J].IEEE/ASMETransactionsonMechatronics,1999,4(4):342-353. [7]STEIND,SCHEINERMANER,CHIRIKJIANGS.Mathematicalmodelsofbinarysphericalencoders[J].IEEE/ASMETransactionsonMechatronics,2003,8(2):234-244. [8] 王群京,陈丽霞.基于加权无向图的永磁球形步进电机运动控制[J].中国电机工程学报, 2005,25(9): 130-134. [9] 王群京,陈丽霞,李争,等.基于光电传感器编码的永磁球形步进电机运动控制[J].中国电机工程学报,2005,25(13):113-117. [10] 过希文,王群京,李国丽,等.基于摩擦补偿的永磁球形电机自适应模糊控制 [J].中国电机工程学报,2011,31(15):75-81. [11] 鞠鲁峰,王群京,李国丽,等.永磁球形电机的支持向量机模型的参数寻优 [J].电工技术学报,2014,29(1): 85-89. [12]WANGJ,WANGW,JEWELLGW,eta1.Anovelsphericalpermanentmagnetactuatorwiththreedegrees-of-freedom[J].IEEETrans.onMagnetics,1998,34(4):2078-2080. [13]WANGW,WANGJ,JEWELLGW,eta1.Designandcontrolofanovelsphericalpermanentmagnetactuatorwiththreedegreesoffreedom[J].IEEE/ASMETransactionsonMechatronics, 2003,8(4): 457-468 . [14]KAHLENK,VOSSI,PRIEBEC,etal.Torquecontrolofasphericalmachinewithvariablepolepitch[J].IEEETransactionsonPowerElectronics,2004,19(6):1628-1634. [15]LIMCK,CHENI-M,YANL,etal.Electromechanicalmodelingofapermanent-magnetsphericalactuatorbasedonmagnetic-dipole-momentprinciple[J].IEEETransactionsonIndustrialElectronics,2009,56(5):1640-1648. [16]YANL,CHENI,LIMC.Modelingandiron-effectanalysisonmagneticfieldandtorqueoutputofelectromagneticsphericalactuatorswithironstator[J].IEEE/ASMETransactionsonMechatronics, 2012,17(6):1080-1087. [17] XIA C L,GUO C,SHI T N.A new algorithm for dynamic decoupling control of HPMSM using fuzzy controllers[C]//IEEE International Conference on Industrial Electronics and Application.IEEE,2008:1031-1035. [18] XIA C L,XIN J G,SHI T.Design and analysis of a variable arc permanent magnet array for spherical motor[J].IEEE Transactions on Magnetics,2012,49(4): 14706-1478. [19] 苏仲飞,刘昌旭,韦平顺,等.机器人关节用三自由度球形直流伺服电动机[J].高技术通讯, 1994(8):16-18. [20] 黄声华,陶醒世.三自由度电动机自适应控制[J].电工技术学报,1998,2(1):10-12. [21] 诸静.球形电动机及其运动轨迹控制[J].中国电机工程学报, 1993,13(5):50-56. [22] LEEH J,PARK H J,RYU G H,et al.Performance improvement of operating three-degree-of-freedom spherical permanent-magnet motor[J].IEEE Transactions on Magnetics,2012,48(11):4654-4657. [23] MULLER P A,BOUCHERIT R,LIN S.Smooth and time-optimal trajectory planning for robot manipulators[C]//2012 American Control Conference.2012:5466-5471. [24] HUANG M S,HSU Y L,FUNG R F.Minimum-energy point-to-point trajectory planning for a motor-toggle servomechanism [J].IEEE/ASME Transactions on Mechatronics, 2012,17(2):337-343. [25] RYMANSAIB Z,IRAVANI P,SAHINKAYA M N.Exponential trajectory generation for point to point motions[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics.2013:906-911. [26] MELIGY R E,BASSIUNY A M,BAKR E M.A feasible minimum-time trajectory of robot manipulator[C]//Proceeding of the 9th International Symposium on Mechatronics and its Application.2013. [27] 刘松国,朱世强,吴文祥.具有时间约束的机械手最优平滑轨迹规划方法[J].电机与控制学报,2009,13(6):897-902. Minimum-Jerk Trajectory Planning of 3-DOF PM Spherical Motor WU Feng-ying,ZHAI Xian-chao,ZHANG Deng-quan,LI Rui (Tianjin University of Technology,Tianjin 300384,China) In order to improve the smoothness and reduce the vibration during the motion of the three degree of freedom permanent magnet spherical motor in the definite time,a minimum-jerk trajectory planning method was proposed .To ensure the jerk continuously, the method used fifth B spline interpolation position sequence, and transformed the kinematic constraints to B spline control points constraint, and took the minimum integral of squared jerk as minimum-jerk performance index.Genetic algorithm was used to seek the minimum-jerk performance index and the corresponding time nodes, and then the global optimization minimum-jerk trajectory planning was got. Finally, the feasibility and effectiveness of the proposed method are verified by simulation experiments. 3-DOF; PM spherical motor; minimum-jerk; B-spline; genetic algorithm 2016-04-20 天津市应用基础与前沿技术研究计划资助项目(14JCYBJC18400) TM351;TM359.9 A 1004-7018(2016)10-0082-04 吴凤英(1961-),女,副教授,研究方向为电机与电器。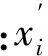
4 仿真实验
5 结 语
