基于相反电动势比较法的无刷电机换相点检测策略的研究

吕腾飞 ，迟长春 ，刘红松，夏业中

(1.上海电机学院， 上海 200240;2.新安乃达驱动技术有限公司， 上海 201108)



基于相反电动势比较法的无刷电机换相点检测策略的研究

吕腾飞1，迟长春1，刘红松1，夏业中2

(1.上海电机学院， 上海 200240;2.新安乃达驱动技术有限公司， 上海 201108)

无刷直流电机无位置传感器控制策略中，能否准确地检测到换相点，关系着电机运行的性能的好坏。以无刷直流电机的无位置传感器控制系统为研究对象，提出了一种基于相反电动势比较法的换相点检测方法。该方法提高了无刷直流电机换向的准确性，简化了无位置传感器控制系统的控制结构。通过理论分析得出换相点的可变化的区间范围，然后对该方法做了深入的理论研究，并通过Multisim仿真软件和实验验证了该方法的有效性和可行性。

直流无刷电机；无位置传感器控制；相反电动势比较；换相点

0 引 言

无位置传感器控制策略有利于降低无刷直流电机的生产成本和维修成本，提高无刷直流电机的经济效益。无位置传感器控制的一项关键技术是电机换相点的检测。当前无刷直流电机无位置传感器控制策略中换相点的检测方法比较多。其中，反电动势检测法中的反电动势过零点检测法是应用最广泛、技术最成熟的方法。

反电动势过零点检测法通过无刷直流电机的相电压与虚拟中性点比较得出反电动势过零点，并通过估算反电动势过零点之后30°电角度所需的时间而得到无刷直流电机的理想换相点，即反电动势过零点后30°电角度的位置[1]。反电动势过零点比较法原理简单，硬件电路不复杂，易于实现，但是其中的软件估算环节不仅增加了软件的计算负担，而且估算过程也导致了换相点误差的存在。与直接检测直流无刷电机的换相点的方法比较，此种方法多了一个软件估算的环节，控制过程较复杂。针对反电动势过零点检测法的不足之处，提出一种新的基于相反电动势比较法的换相点检测方法，来提高无刷直流电机换相的准确性和快速性。

1 基于反电动势比较法换相点捕捉方法的研究

无刷直流电机三相全桥式控制结构图[2]如图1所示。

图1 无刷直流电机三相全桥式控制结构图

无刷直流电机在正常运行的过程中，电机的三相绕组电压方程[3-4]可简化如下：

(1)

即:

(2)

式中：Ux为无刷直流电机的x相的相电压，x=a，b，c；ix为无刷直流电机的x相的相电流，x=a，b，c；ex为无刷直流电机的x相的反电动势，x=a，b，c；R为为定子三相绕组的电阻；M为相绕组之间的互感；L为三相绕组的自感；p为微分算子d/dt。

根据电机学原理，反电动势可表示[5]：

(3)

式中:ω为电机电角速度；Bm为转子永磁体气隙磁密分布的最大值；ke为反电动势系数， ke=2NSBm；N为绕组匝数；S为绕组围成的面积；fa(θ)为相反电动势的波形函数，其最大值和最小值分别为1和-1。

现以A相、C相为例，来说明本文的换相点检测原理。为了得到A相的换相点，将C相反电动势与A相反电动势比较，如图2所示。由无刷电机的控制原理可知，两相反电动势的交点即为理论的最佳换相点[6]。

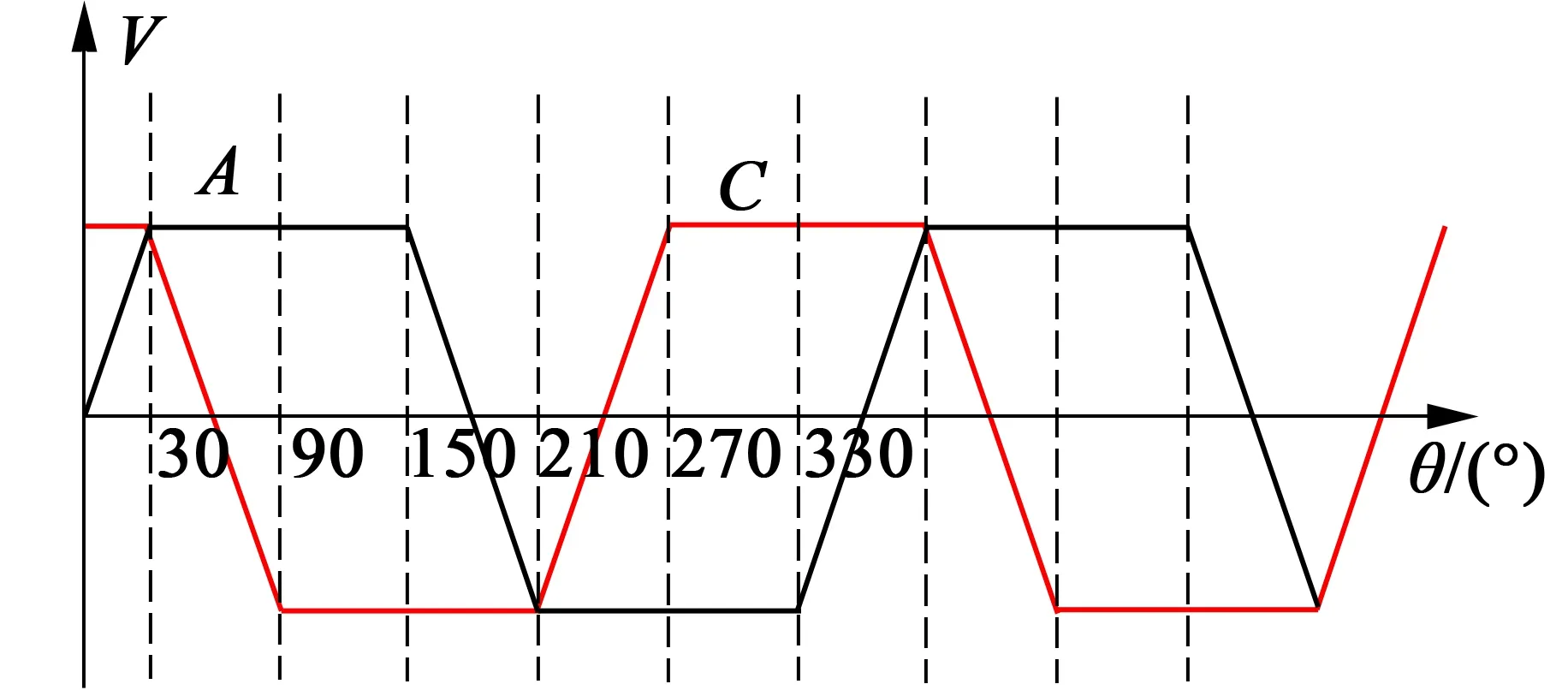
图2 A、C两相反电动势比较图

在两相反电动势波形相交的位置，即理论最佳换相点处：

(4)

先假设在理论最佳换相点处，A相、C相电流相等(实际上不会出现这种情况)，即：

(5)

把式(4)、式(5)代入式(2)得：

(6)

由于电机定子绕组的反电动势不能直接测量，由以上分析可知，在A相的最佳换相点处，A相和C相的相电压相等，所以可以通过测量定子绕组的相电压来直接捕捉换相点。即换相点为两相电压相等的时刻。

以上分析的结论是建立在假设式(5)成立的基础上，但实际上在检测到A相的换相点之前，A相、C相电流不相等，即式(5)不成立。具体说明如下：假设现在处于B相、C相导通的状态，下一个导通状态是A相、B相导通。电机控制系统现在正在检测A相的换相点。在检测到换相点之前，即图3中D点的位置。

图3 无刷直流电机理想的三相反电动势波形与电流波形关系图

各相电流状态如下：

(7)

式中： I为相电流。

显然，此时A相、C两相电流不相等。

为了使用式(6)的结论，本文把C相的反电动势波形延迟(360°-θ)，0°≤θ≤30°。如图4所示。

图4 A相反电动势和移相后的C相反电动势波形图

在A相反电动势和延迟后的C相反电动势交点E处：

(8)

由以上分析可知，C相波形移相后，在A相、C相电压波形的交点处，故：

(9)

即：

(10)

下面证明这一充要条件的正确性。

由图4可知，在一个周期内，A、C两相反电动势波形有两个交点。由以上结论可知，这两个交点处对应的相电压波形相交。由图5可知，A、C两相电压波形在一个周期内也有且只有两个交点。由此证明A、C两相电压波形交点与A、C两相反电动势波形的交点一一对应。从而证明了式(10)的正确性。

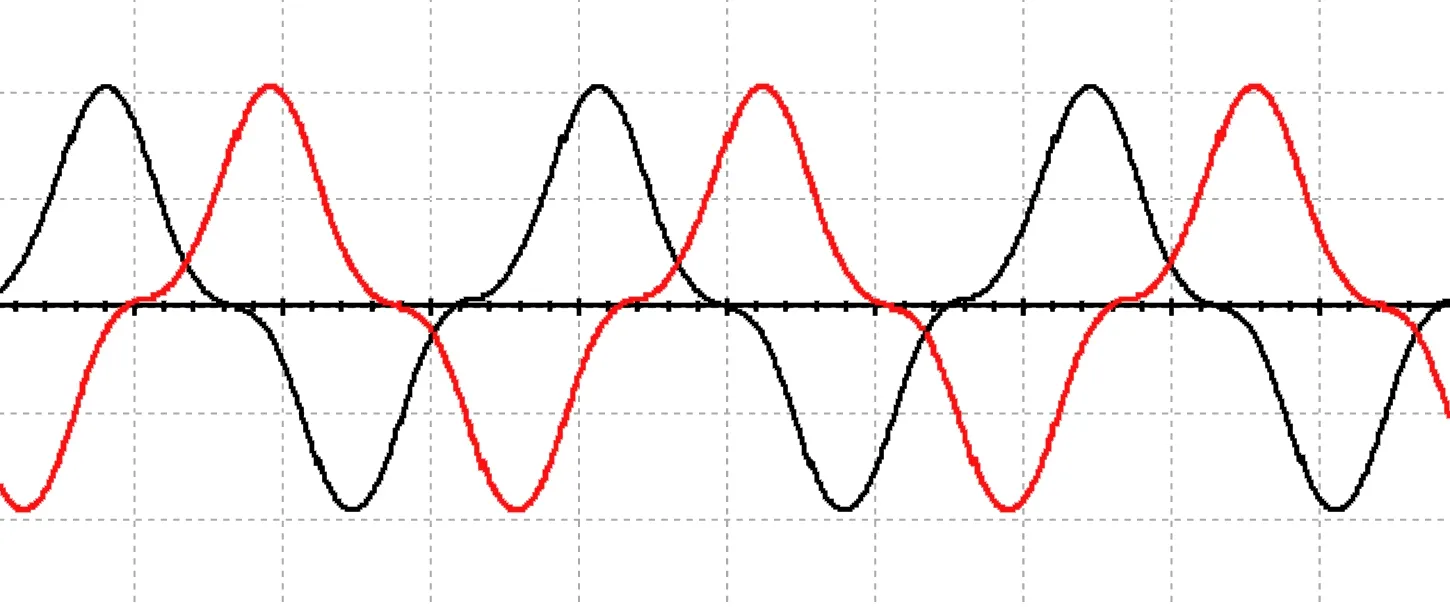
图5 滤波后A、C两相电压仿真波形图

本文设计的基于反电动势比较的换相点捕捉电路简化电路图如图6所示。图中低通滤波器可以去除三路相电压中的高频杂波，得到稳定、纯净的电压波形。电路中电容起到延迟移相的作用。具体分析如下。

图6 换相点检测电路

如图6所示，三路相电压经过滤波之后，A相电压和延迟后的C相电压通过比较器比较得到两相电压相等的时刻，即A相的换相点。同理，B相电压和延迟后的A相电压比较得到B相的换相点，C相电压和延迟后的B相电压比较得到C相的换相点。

由于低通滤波器的存在，上述电路得到的换相点会比理想最佳换相点滞后一定的电角度[7]。由下文理论分析可知，换相点在理想换相点前后30°电角度范围内都是可以接受的，所以通过调节电路参数，只要保证实际换相点在允许的换相范围之内即可。

2 无刷直流电机换相点可变化范围的理论分析

反电动势波形为120°平顶宽度的梯形波无刷直流电机，通常采用三相六状态120°通电方式[8]。当换相点处于理想位置，即图7中B点时，三相反电动势波形与电流波形的关系如图7所示。

图7 无刷直流电机理想的三相反电动势波形与电流波形的关系图

图7中，换相点在反电动势过零点后的30°电角度的位置，此换相点是最理想的换相位置。但换相点不是唯一的，经理论分析可知，可接受的换相位置的区间是理想换相点的前后30°电角度之间，即A相C相之间的电角度区间范围，具体分析如下。

假设电机磁极对数为 1，电机转子初始位置如图8 中A图所示， AX,BY 和 CZ 为电机三相定子绕组，连接方式为星形连接。图8中，Fa与 Fb分别为a、b 相定子电流产生的磁势，Fs为Fa与 Fb的合成磁势，Fr为转子永磁体产生的磁势。

(a)(b)

图8 理想换相时一个换相周期内转子始末位置示意图

由于定子合成磁势与转子磁势的夹角为90°时产生的转矩最大[9]，直流无刷电机的驱动电路的换相周期为60°。所以无刷直流电机在理想换相点换相时，驱动电路每个周期的导通区间为Fs与Fr夹角为120°到60°的区间，一个换相周期内转子位置始末位置如图8所示。图8(a)为一个导通状态之初转子的位置，图8(b)为一个导通之末转子的位置。此时换相点为定子绕组不导通相的反电动势过零点后30°的位置，即图7中B点。

当驱动电路每个周期的导通区间为Fs与Fr夹角为150°到90°的区间时，即A点换相模式，一个换相周期内转子位置始末位置如图9所示。图9(a)为一个导通状态之初转子的位置，图9(b)为一个导通之末转子的位置。研究证明(德国MK项目的BL-Ctrl电调方案[10])，A点换相时直流无刷电能够机正常工作，但与理想换相位置比较，电机在A点换相模式下工作时，效率略低。此时的换相点为定子绕组不导通相的反电动势过零点，即图7 中A点。

(a)(b)

图9 A点换相时一个换相周期内转子始末位置示意图

同理,当驱动电路每个周期的导通区间为Fs与Fr夹角为90°到30°的区间时，即C点换相模式，一个换相周期内转子位置始末位置如图10所示。图10(a)为一个导通状态之初转子的位置，图10(b)为一个导通之末转子的位置。转矩大小的变化范围和A点换相模式的相同，只是变化方向相反，工作效果和A点换相模式相同。此时的换相点为定子绕组不导通相的反电动势过零点后60°电角度的位置，即图7 中C点。

(a)(b)

图10 C点换相时一个换相周期内转子始末位置示意图

综上所述，可接受的换相点变化区间为定子绕组不导通相的反电动势过零点到过零点后60°电角度的区间，即图7 中A点到C点之间的区间。由以上结论可知，通过调节电路参数，保证实际换相点在理论换相点的前后30°电角度之内，都可以实现电动自行车无刷直流电机的成功换相。

由以上分析可知，通过采用反电动势比较法的换相点检测方法可以直接得到无刷直流电机的换相点，与现有的反电动势过零点检测法相比较，该方法省略了其软件估算环节，既避免了估算环节造成的误差，又简化了无刷直流电机无位置传感器控制系统的结构，相对提高了无刷直流电机换相点捕捉的准确性和控制系统响应的快速性。

3 电路仿真及结果分析

为验证上述基于反电动势比较法的换相点捕捉电路的有效性，本文用仿真软件Multisim建立了仿真系统。电机参数为：电机极对数p=6；额定电压 UN=48V； 转矩常数K=0.03；速率常数Kn=0.03；定子电阻R=0.6Ω；定子电感 L=0.15mH。

图11是电机转矩为 0.1N·m、转速为 3 000r/min时A相、C两相电压经过换相点检测电路中的低通滤波器之后的仿真波形。其中，Ⅰ是经过滤波后进入比较器的A相电压波形，Ⅱ是经过滤波并延迟移相(360° -θ)后的C相电压波形。

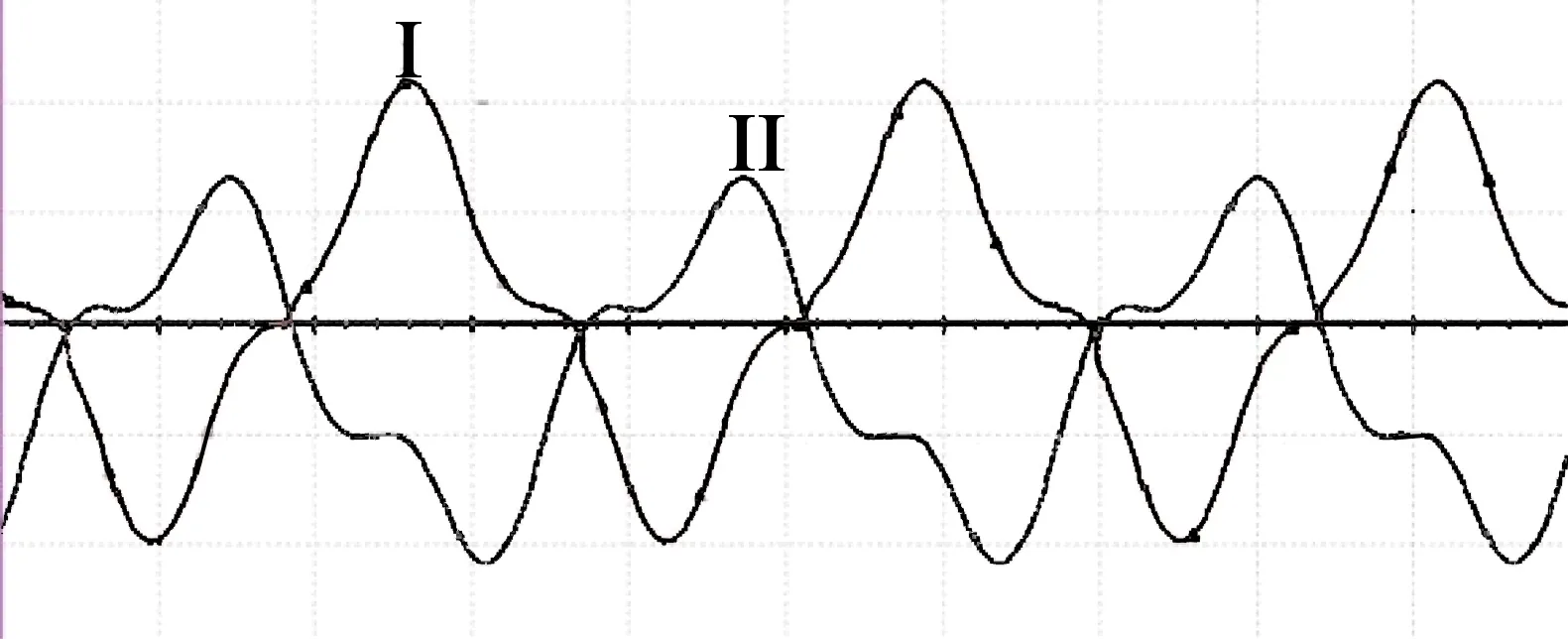
图11 比较电路输入波形

图12是电动自行车的理想换相点和实际换相点的比较波形。图12中Ⅰ为无刷直流电机中的霍尔传感器输出的代表换相位置的波形，即理想换相点捕捉波形;Ⅱ为本文设计的换相点捕捉电路输出的代表换相位置的波形，即实际换相点捕捉波形。其中，方波跳变的位置即为换相点。从图12中可以看出，由于低通滤波器的存在，实际换相点与理想换相点存在一定误差[11]。在转速为3 000r/min误差为25°电角度，在转速小于3 000r/min范围内，误差小于25°电角度。由于电动自行车控制系统的电机最大空载转速约为500r/min，远小于3 000r/min，所以换相点捕捉电路输出的换相点在上述分析的可变化范围内，无刷直流电机可以正常工作[12]。本仿真结果验证了本文设计的基于反电动势比较法的换相点检测方案和电路的正确性。

图12 理想换相点捕捉波形及实际换相点捕捉波形

4 实验验证及结果分析

本文将设计的无刷直流电机无位置传感器换相点检测电路移植到某公司的S91-T5控制器上，通过实验证明本文所设计的换相点捕捉电路的可行性。本文以改进后的S91-T5控制器和额定电压48V，额定电流15A，输出功率350W，最大转速400r/min的无刷直流电机为实验平台，对本文提出的理论进行了实验验证。

无位置传感器控制系统的控制原理图如图13所示。

图13 无刷直流电机无位置传感器控制框图

图14、图15为基于反电动势比较法的换相点捕捉电路中比较器的输入输出波形，其中Ⅰ为A相电压滤波后的波形，Ⅱ为C相电压经过滤波并延迟移相后的波形，Ⅲ为比较器的输出波形，方波跳变的位置即为电机绕组换相的位置。由本文第1章理论分析可知，图14中，两相电压波形的交点即为A相绕组的换相点。从图15可以看出，比较器输出方波的跳变位置正对应图14中两波形的交点。所以比较器输出方波的跳变点即为A相绕组的换相点。方波作为换相点的检测信号被输送到控制系统的核心芯片STM8S，STM8S根据换相点的位置控制电机定子三相绕组的通断。

图14 比较电路输入波形

图15 比较电路输入波形和输出波形对比图

图16、图17分别为电机高速运转和低速运转时， 本文设计的换相点检测电路的输出波形和霍尔传感器检测电路的输出波形的比较图。其中，Ⅰ为霍尔电路输出的换相点信号波形，Ⅱ为本文设计的基于反电动势比较法的换相点检测电路输出的换相点信号波形。图中，方波跳变的位置即为换相点。由图中可以看出，由于低通滤波器的存在，本文检测电路输出的换相点信号波形与理想换相点信号波形(霍尔电路测得的换相点)存在一定误差。当电机低速运行时，如图17测得的换相点滞后理想换相点3.7°电角度；高速运行(电机空载，转把转到最大极限位置是的速度)时，如图16测得的换相点滞后理想换相点13.1°电角度。换相点滞后电角度在第2章分析的可变化范围内，无刷直流电机可以正常工作。本实验证明了本文基于反电动势比较法的换相点捕捉策略的可行性。

图16 高速时换相点捕捉信号与霍尔信号

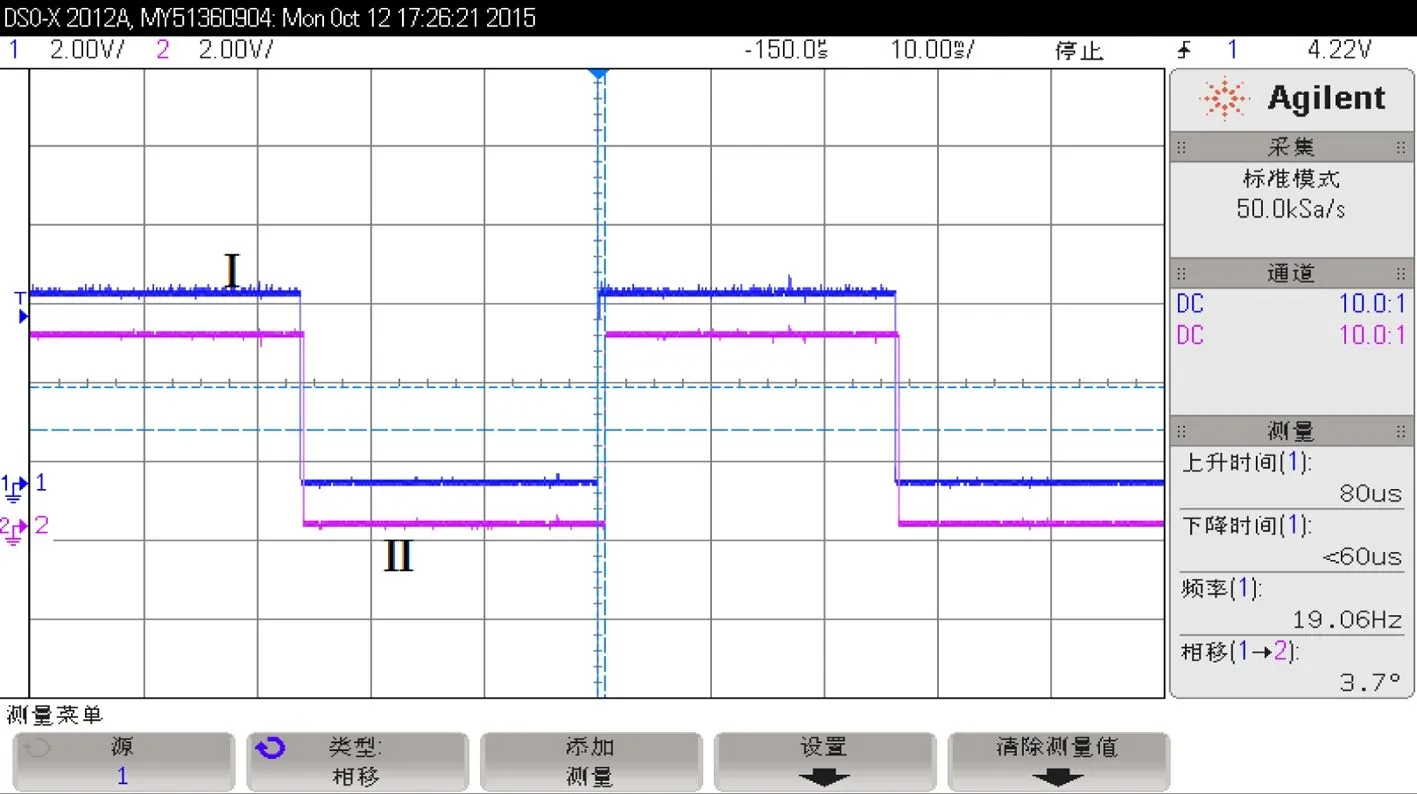
图17 低速时换相点捕捉信号与霍尔信号

5 结 语

无刷直流电机无位置传感器控制策略中换相点检测的准确性和快速性，对电机的运行性能至关重要。提出的基于相反电动势比较法的换相点检测策略，采用相反电动势比较法直接得到无刷直流电机的换相点。与现有的反电动势过零点检测法相比较，该方法省略了其的软件估算环节，既避免了估算环节造成的误差，又简化了无刷直流电机无位置传感器控制系统的结构。从理论上提高了换向检测的准确性和快速性。通过Multisim仿真软件及实验验证了其合理性和有效性，其结果证明了该方案能成功检测到无刷直流电机的换相点，验证了其在无刷直流电机控制领域的可行性。

[1] 孟光伟,李槐树,熊浩.无位置传感器无刷直流电机的起动控制原理与研究[J].防爆电机,2010,4(2):20-22,36.

[2] 张博岚.无位置传感器无刷直流电机控制系统的研究[D].长沙:湖南大学，2010.

[3] 王雷.基于STM8S903K3的电动自行车控制器设计与实现[D].南京:南京理工大学,2014.

[4] 宋海龙,杨明,范宇,等.无刷直流电动机的无位置传感器控制[J].电机与控制学报,2002，6(3):33-37.

[5] 李志强,夏长亮,陈炜.基于线反电动势的无刷直流电机无位置传感器控制[J].电工技术学报,2010,25(7): 38-44.

[6] 彭钰珍.小容量无刷直流电动机无位置传感器控制技术的研究[D].武汉:华中科技大学,2007.

[7] OGASAWARA S,AKAGI H.An approach to position sensorless drive for brushless DC motors[J].IEEE Transactions on Industry Applications,1991,27(5): 928-933.

[8] RODRIGUEZ F,EMADI A.A novel digital control technique for brushless DC motor drives[J].IEEE Transactions on Industrial Electronics,2007,54(5):2365-2373.

[9] HSIEH M-F,LIAO H-J.A wide speed range sensorless control technique of brushless dc motors for electric propulsors[J].Journal of Marine Science and Technology-Taiwan,2010,18(5):735-745.

[10] 墨鸢.无感无刷直流电机之电调设计全攻略[Z/OL].[2016-02-01].http://www.amobbs.com/thread-4164837-1-1.html.

[11] ISLAM M N.Sensorless position control for piezoelectric actuators using a hybrid position observer[J].IEEE/ASME Transactions on Mechatronics,2014,19(2):667-675.

[12] LÜ Tengfei,CHI Changchun.Research on sensorless control strategy of motor controller for electric bicycle[C]//IC3ME 2015.Atlantis Press,2015:1291-1295.

Research on the Reversing Point Capture Method of Position Sensorless Control System of BLDCM

LÜ Teng-fei1, CHI Chang-chun1, LIU Hong-song1， XIA Ye-zhong2

(1.Shanghai Dianji University,Shanghai 200240,China;2.Ananda Drive Techniques Co.,LTD.,Shanghai 201108,China)

Whether the change point of the phase of brushless DC motor (BLDCM) can be accurately captured in the brushless DC motor sensorless control strategy, decide that the performance of the motor is good or bad. Taking the sensorless control system of brushless DC motors as the research object, a kind of reversing point capture method was proposed. At the same time, the range of the reversing point was demonstrated by theoretical analysis. And the effectiveness of the designed circuit was verified by the Multisim.

brushless DC motor; sensorless control; comparison of the back electromotive force; reversing point

2016-02-29

上海市闵行区科技项目 (2014MH134)；上海市自然科学基金项目(12zr1411700)；上海电机学院校研究生创新项目(A10225-15-005-08)

TM33

A

1004-7018(2016)10-0074-04

吕腾飞(1990-)，男，硕士，研究方向为电机与智能电器。