振动式压电风能发电装置的研究
2016-12-20张健滔
吴 松,张健滔
(上海大学, 上海 200072)
振动式压电风能发电装置的研究
吴 松,张健滔
(上海大学, 上海 200072)
建立了振动式压电风能发电装置在风流场中的有限元分析模型。基于标准k-ε模型进行了风流场仿真分析,并通过系统耦合实现了风流场和发电装置固体之间的双向耦合分析。获得了压电发电装置在风流体作用下的振动特性结果,结果显示:发电装置在流场中径向放置比其他放置方式能产生更多的电能。制作了压电发电装置,并在微型风洞中进行了实验。结果表明,发电装置在风场中径向放置时产生的电压明显比其他放置方式高,当风速为15 m/s时,径向放置的输出电压峰峰值大约是轴向放置的两倍。
压电发电装置;流固耦合;振动;有限元
0 引 言
近年来,随着无线传感网络以及微型电子设备的飞速发展,对这些设备的供能成为迫切需要解决的问题。传统的化学电池供能具有其不足,例如电池体积大、能量密度低、使用寿命有限、 需定期更换、成本高、旧电池处理不当会对环境产生污染。因而从环境中寻找新的能源替代传统电池供电成为国内外研究的热点[1-4]。
风能作为自然界中的绿色可再生能源,安全、清洁、资源丰富、取之不竭,存在很大的利用价值。微型风能发电装置可将风动能转变为电能进而为微电子设备供能,其具有广阔的发展前景。其中压电式风能发电装置由于具有结构简单、能量密度大、无电磁干扰、启动风速低、易于微型化等特点,国内外学者都展开了相应的研究[5-8]。
从结构特点来看,压电式风能发电装置可分为涡轮旋转式和风致振动式两种。Ying Yang等人提出了一款涡轮旋转式压电风能发电装置,其通过风带动旋转装置,进而使球跳动并撞击压电悬臂梁变形,从而产生电荷[9]。Karami等研制了一款微型风力涡轮发电装置,其在转动元件和压电悬臂梁的末端都装上永磁体,转动元件通过永磁体的相互作用带动压电悬臂梁往复振动,从而产生电能[10]。D. St. Clair从乐器口琴获得启发,设计了一款微型自激振动压电风能发电装置[11]。Xue-Feng He提出了一款低启动风速的压电振动风能发电装置,其通过风引起金属悬臂梁撞击挡板产生冲击效果,进而致使压电发电装置振动,发电装置的启动风速为3.2~3.4 m/s[12]。
振动式压电风能发电装置由于其结构简单、启动风速较低等特点,受到了研究者的青睐。但如何提高发电装置的能量转换效率是一个值得研究的问题。本文将对振动式压电风能发电装置在流场中的放置方式对能量采集效率的影响进行研究。建立了压电风能发电装置在流场中的有限元分析模型,分析了其在流场中不同放置方式下的应变结果,并在小型风洞中测试了发电装置在不同放置方式下的输出电压。结果表明:发电装置在流场中合理放置能有效地提高其能量收集性能。
1 流固耦合有限元分析模型
振动式压电风能发电装置工作过程中涉及两个能量转换过程:空气动能致使发电装置的压电元件产生振动,风能转换为机械能;然后再利用压电材料的正压电效应将机械能转换为电能。在能量的转换过程中,压电悬臂梁振动应变大小直接影响发电装置的发电能力。因此,本文将建立振动式压电风能发电装置在风流场中的有限元分析模型,对比分析发电装置在不同放置方式下的振动应变情况。
图1是发电装置在风流场中的放置方式示意图。在同一平面内,通过改变压电装置与风向所成夹角α来变化压电装置的放置方式。其中,当夹角α为0°时,压电悬臂梁呈轴向放置;夹角α为90°时,压电悬臂梁呈径向放置。
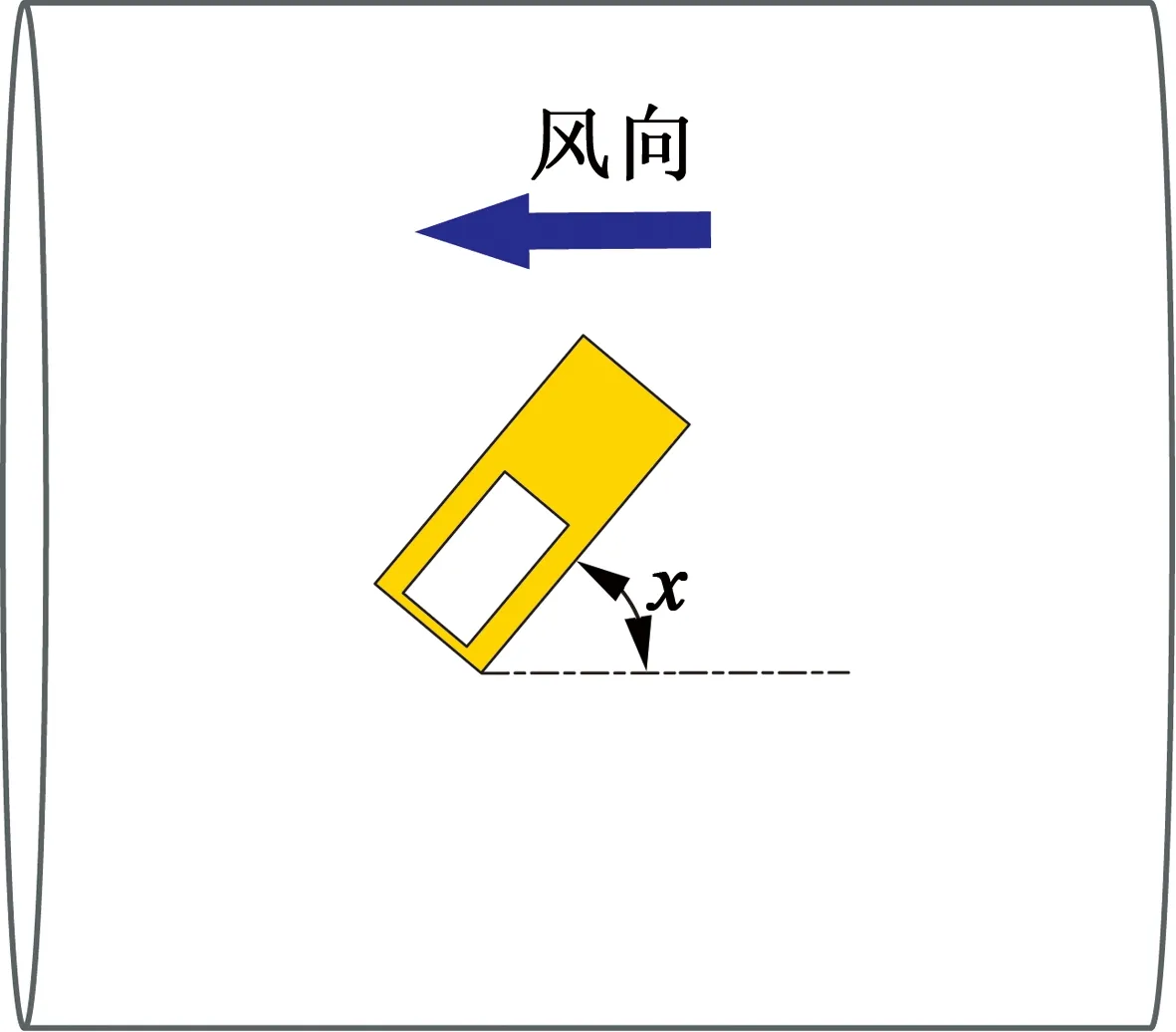
图1 发电装置在风流场中的放置方式示意图
通过三维设计软件建立有限元分析的几何模型,如图2所示。该几何模型包括由压电悬臂梁组成的固体域以及类似风洞腔体的流体域,流体域的尺寸与风洞实验段尺寸相同。压电悬臂梁在流场中放置方式包括四种:沿流体腔轴向放置、沿流体腔径向放置、与风向呈45°放置和与风向呈90°放置。流体域中以空气为介质,压电悬臂梁的金属体材料为纯铜,压电陶瓷片为PZT-5。

(a)压电悬臂梁轴向放置(b)压电悬臂梁径向放置(c)压电悬臂梁45°放置(d)压电悬臂梁135°放置
图2 有限元分析的几何模型
将几何模型导入有限元软件中,流体域和固体域分别在Fluent模块和Transient structural模块下进行网格划分,建立有限元模型如图3所示。其中流体域的单元尺寸设为8 mm,网格单元数量达到111 387;固体域的单元尺寸设为1 mm,单元数量为2870。在流体计算中采用了标准k-ε模型。标准k-ε模型通过求解湍动能k方程和湍流耗散率ε方程,得到k和ε的解,再利用k和ε计算湍动粘度。标准k-ε模型具有较高的计算精度、较好的稳定性和计算经济性,在湍流模型中得到了广泛的应用。
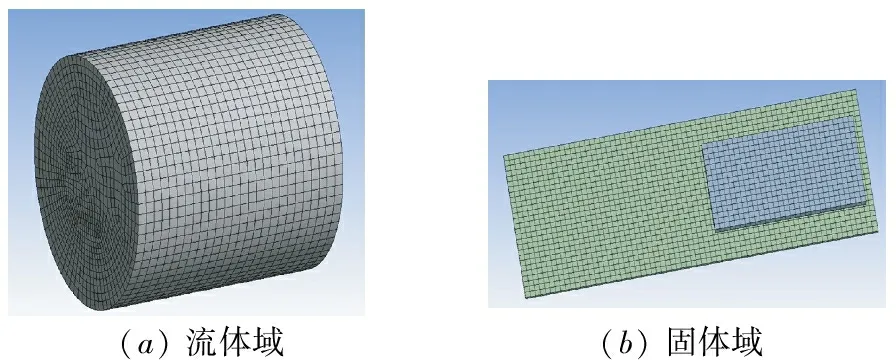
(a)流体域(b)固体域
图3 有限元模型
设置流场入口风速为10 m/s。流固耦合数值计算是一个双向流固耦合的求解过程:先根据初始状态,求解出流场的流动;然后通过系统耦合将耦合边界上的流场计算结果传递给发电装置,通过固体的瞬态结构分析求解出发电装置的位移变化;瞬态分析结果又通过系统耦合传递给流场,之后又是流场分析计算。如此重复进行迭代计算,当求解结果趋于稳定,流场和瞬态分析数据交换停止,计算终止。
图4为压电悬臂梁在流场中四种放置方式下的应变结果图,压电悬臂梁应变最大的地方靠近固定端。对比四种放置方式下的结果,发现径向放置时压电陶瓷上的最大应变为轴向放置时压电陶瓷上的最大应变的10倍;压电悬臂梁45° 放置时压电陶瓷上的最大应变为135° 放置时的3倍左右,且是轴向放置的4倍左右。即随着夹角α从0° 增加到135°,压电陶瓷上的最大应变先增大后减少。由压电体所受应力及产生电场的本构关系可知,压电体上的应变增加会致使产生的电场强度增强[1]。由此,结合压电风能发电装置有限元分析结果可知:发电装置在流场中径向放置时能产生更多的电能。

(a) 压电悬臂梁轴向放置
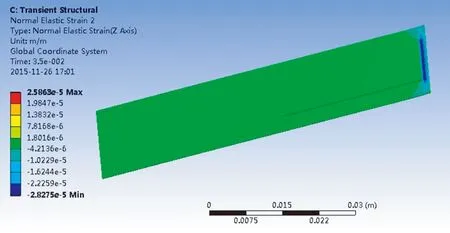
(b) 压电悬臂梁径向放置

(c) 压电悬臂梁45°放置

(d) 压电悬臂梁135°放置
2 压电发电装置实验
根据设计结果制作出压电发电装置,其中压电材料采用压电陶瓷PZT-5,尺寸为30 mm×16 mm×0.5 mm,基板材料为纯铜,尺寸为70 mm×26.5 mm×0.2 mm。实验设备如图5所示,包括微型风洞、风速计(TASI-8818)、示波器(TBS 1102, Tektronix)。压电发电装置放置在风洞的透明实验段,通过两块亚克力板夹持固定在一根螺柱上,如图6所示,其中图6(a)、图6(b)、图6(c)、图6(d)分别是压电悬臂梁轴向放置、径向放置、45°和135°放置时的状态。

图5 实验装置图

(a)压电悬臂梁轴向放置(b)压电悬臂梁径向放置(c)压电悬臂梁45°放置(d)压电悬臂梁135°放置
图6 压电悬臂梁在风洞中的放置方式
测试出压电发电装置随风速变化的曲线图,如图7所示。风速为从3 m/s增加到15 m/s,通过示波器记录发电装置的输出电压峰峰值,多次测量取平均。从图7可以看出,随着风速的增加,发电装置的输出电压峰峰值也不断增加。随着发电装置在风场中的夹角不断增大,其产生的电压先增大后减少,且当风速为15 m/s时,径向放置时的输出电压峰峰值大约是轴向放置时的2倍。

图7 风速与输出电压的关系曲线
3 结 语
本文建立了振动式压电风能发电装置在风流场中的有限元分析模型。利用标准k-ε模型来分析风流场,通过系统耦合实现了风流场和发电装置固体之间的双向耦合分析。获得了发电装置在风流体作用下的振动特性结果,结果表明:相对其他几种放置方式,发电装置在流场中径向放置时能产生更多的电能。在微型风洞实验装置中,对分析结果进行了实验验证。实验结果显示:随着发电装置在风场中的夹角α的增大,其产生的电压先增大后减少,且当风速为15 m/s时,径向放置时的输出电压峰峰值大约是轴向放置时的2倍。
[1] 宁玉怀.压电发电的能量转化及储能技术研究[D].长沙:中南大学,2010.
[2] PARK J C,PARK J Y.Asymmetric PZT bimorph cantilever for multi-dimensional ambient vibration harvesting[J].Ceramics International, 2013,39(1):5653-5657.
[3] 邓冠前.基于压电陶瓷的振动能量捕获关键技术研究[D].北京:国防科学技术大学,2008.
[4] 王剑,郭吉丰,郭帅.压电发电技术研究综述.压电与声光[J].2011, 33(3): 394-398.
[5] KHALID M S,HOSSAM S A,MAZLAN A W,et al.Numerical simulation of confined vortex flow using a modifiedk-εturbulence model[J].CFD Letters, 2009,1(2): 87-94.
[6] KWON S D.A T-shaped piezoelectric cantilever for fluid energy harvesting[J].Applied Physics Letters, 2010,97(16): 1-3.
[7] 董志利,张广明,徐飞.压电陶瓷风力发电机的创新设计[J].微特电机,2014,42(1): 25-27.
[8] 周铁英,鹿存跃,陈宇.毫米压电微电机的发展与应用[J].微特电机,2005,33(12):41-44.
[9] YANG Ying,SHEN Qinlong.Rotational piezoelectric wind energy harvesting using impact-induced resonanceors[J].Applied Physics Letters, 2014,105(5): 053901.
[10] KARAMI M A,FARMER J R,INMAN D J.Parametrically excited nonlinear piezoelectric compact wind turbine[J].Renewable Energy,2013,50(3): 977-987.
[11] ST CLAIR D,BIBO A.A scalable concept for micropower generation using flow-induced self-excited oscillations[J].Applied Physics Letters, 2010,96(14): 144103.
[12] HE Xuefeng,GAO Jun.Wind energy harvesting based on flow-induced-vibration and impact[J]. Microelectronic Engineering,2013,111(11):82-86.
Piezoelectric Wind Energy Harvester Based on Vibration
WU Song, ZHANG Jian-tao
(Shanghai University, Shanghai 200072, China)
The finite element model for the piezoelectric wind energy harvester is developed. The wind flow field was simulated using the standard k-ε turbulence model. The fluid-structure interaction between the flow and the energy harvester was analyzed using system coupling. The vibration characteristics of the energy harvester were obtained, which was acted upon by the force exerted by the wind flow. The results show that the energy harvester placed along the radial direction can generate more electric power than that placed along the other direction. An energy harvester was fabricated and wind-tunnel experiments were carried out. The experimental results show that the energy harvester placed along the radial direction can generate higher voltage than that placed along the other direction. When the wind velocity is 15m/s, the output voltage peak-peak value of the harvester placed along the radial direction is about two times of that placed along the axial direction.
piezoelectric energy harvester; fluid-structure interaction; vibration; finite element method
2015-12-04
国家自然科学基金项目(51305248);上海市自然科学基金项目(13ZR1416900);上海高校青年教师培养计划项目(ZZSD13051);上海大学创新基金项目(SDCX 2012025)。
TM315;TM359.9
A
1004-7018(2016)10-0010-03
吴松(1990-),男,硕士,研究方向为压电能量收集器。
